Thermoelectric Properties of Pnma and Rocksalt SnS and SnSe
Abstract
:1. Introduction
2. Computational Modelling
3. Results and Discussion
3.1. Structure and Lattice Dynamics
3.2. Electronic Structure and Transport Properties
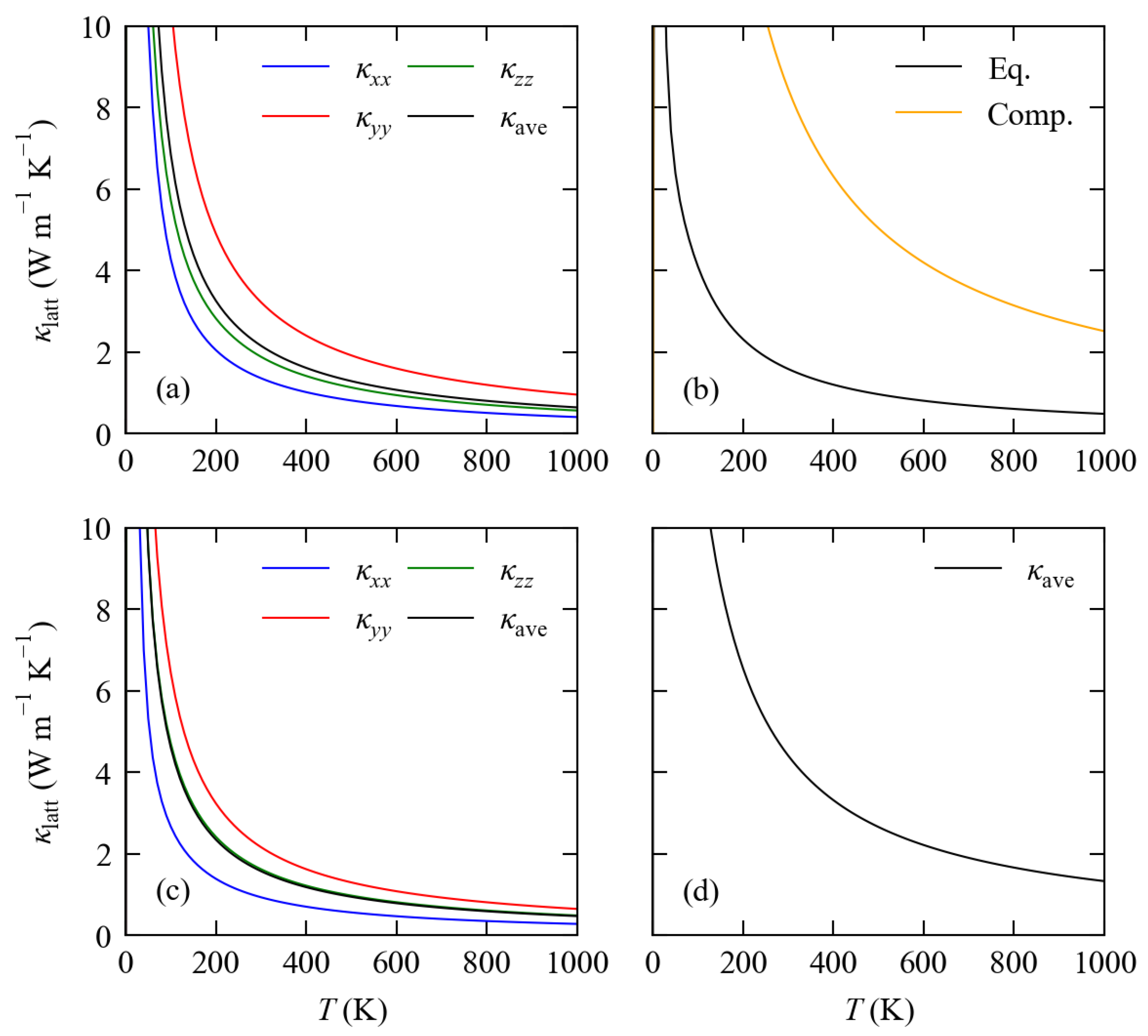
3.3. Lattice Thermal Conductivity
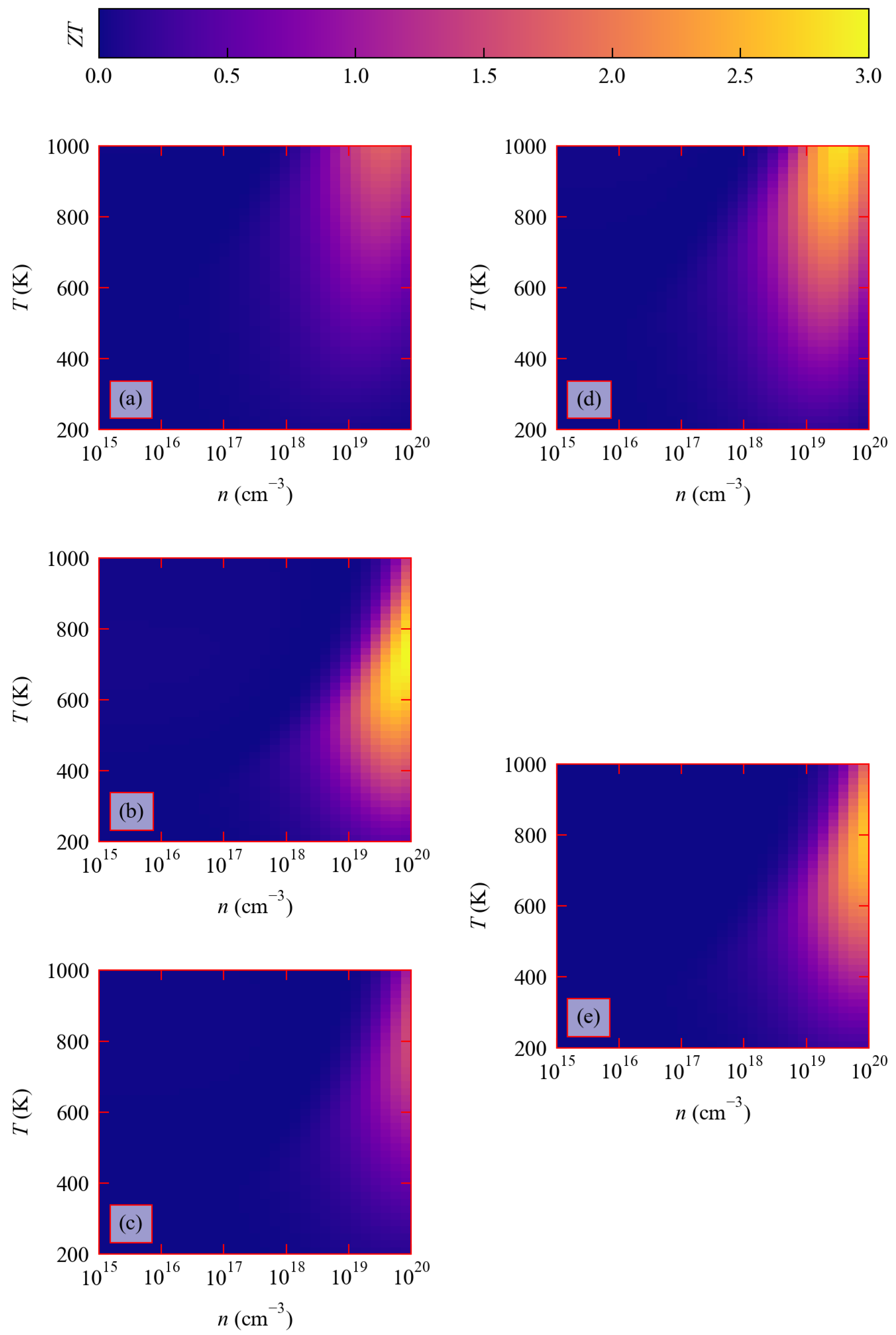
3.4. Thermoelectric Figure of Merit
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tan, G.; Zhao, L.D.; Kanatzidis, M.G. Rationally Designing High-Performance Bulk Thermoelectric Materials. Chem. Rev. 2016, 116, 12123–12149. [Google Scholar] [CrossRef] [PubMed]
- Freer, R.; Powell, A.V. Realising the potential of thermoelectric technology: A Roadmap. J. Mater. Chem. C 2020, 8, 441–463. [Google Scholar] [CrossRef]
- Yan, Q.; Kanatzidis, M.G. High-performance thermoelectrics and challenges for practical devices. Nat. Mater. 2021. [Google Scholar] [CrossRef] [PubMed]
- Zeier, W.G.; Zevalkink, A.; Gibbs, Z.M.; Hautier, G.; Kanatzidis, M.G.; Snyder, G.J. Thinking Like a Chemist: Intuition in Thermoelectric Materials. Angew. Chem. Int. Ed. 2016, 55, 6826–6841. [Google Scholar] [CrossRef] [PubMed]
- Li, C.W.; Hong, J.; May, A.F.; Bansal, D.; Chi, S.; Hong, T.; Ehlers, G.; Delaire, O. Orbitally driven giant phonon anharmonicity in SnSe. Nat. Phys. 2015, 11, 1063–1069. [Google Scholar] [CrossRef]
- Aseginolaza, U.; Bianco, R.; Monacelli, L.; Paulatto, L.; Calandra, M.; Mauri, F.; Bergara, A.; Errea, I. Phonon Collapse and Second-Order Phase Transition in Thermoelectric SnSe. Phys. Rev. Lett. 2019, 122, 075901. [Google Scholar] [CrossRef] [Green Version]
- Aseginolaza, U.; Bianco, R.; Monacelli, L.; Paulatto, L.; Calandra, M.; Mauri, F.; Bergara, A.; Errea, I. Strong anharmonicity and high thermoelectric efficiency in high-temperature SnS from first principles. Phys. Rev. B 2019, 100, 214307. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, M.D.; Ozolins, V.; Heremans, J.P. Lone pair electrons minimize lattice thermal conductivity. Energy Environ. Sci. 2013, 6, 570–578. [Google Scholar] [CrossRef]
- Biswas, K.; He, J.; Blum, I.D.; Wu, C.I.; Hogan, T.P.; Seidman, D.N.; Dravid, V.P.; Kanatzidis, M.G. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 2012, 489, 414–418. [Google Scholar] [CrossRef] [PubMed]
- Gibbs, Z.M.; Kim, H.; Wang, H.; White, R.L.; Drymiotis, F.; Kaviany, M.; Jeffrey Snyder, G. Temperature dependent band gap in PbX (X = S, Se, Te). Appl. Phys. Lett. 2013, 103, 262109. [Google Scholar] [CrossRef]
- Delaire, O.; Ma, J.; Marty, K.; May, A.F.; McGuire, M.A.; Du, M.H.; Singh, D.J.; Podlesnyak, A.; Ehlers, G.; Lumsden, M.D.; et al. Giant anharmonic phonon scattering in PbTe. Nat. Mater. 2011, 10, 614–619. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, W.; Lukas, K.C.; McEnaney, K.; Lee, S.; Zhang, Q.; Opeil, C.P.; Chen, G.; Ren, Z. Studies on the Bi2Te3–Bi2Se3–Bi2S3 system for mid-temperature thermoelectric energy conversion. Energy Environ. Sci. 2013, 6, 552–560. [Google Scholar] [CrossRef]
- Cen, J.; Pallikara, I.; Skelton, J.M. Structural Dynamics and Thermal Transport in Bismuth Chalcogenide Alloys. Chem. Mater. 2021, 33, 8404–8417. [Google Scholar] [CrossRef]
- Korkosz, R.J.; Chasapis, T.C.; Lo, S.h.; Doak, J.W.; Kim, Y.J.; Wu, C.I.; Hatzikraniotis, E.; Hogan, T.P.; Seidman, D.N.; Wolverton, C.; et al. High ZT in p-Type (PbTe)1−2x(PbSe)x(PbS)x Thermoelectric Materials. J. Am. Chem. Soc. 2014, 136, 3225–3237. [Google Scholar] [CrossRef]
- Ginting, D.; Lin, C.C.; Rhyee, J.S. Synergetic Approach for Superior Thermoelectric Performance in PbTe-PbSe-PbS Quaternary Alloys and Composites. Energies 2020, 13, 72. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Li, X.; Ren, Z.; Zhang, Q. Recent progress towards high performance of tin chalcogenide thermoelectric materials. J. Mater. Chem. A 2018, 6, 2432–2448. [Google Scholar] [CrossRef]
- Shi, Y.; Sturm, C.; Kleinke, H. Chalcogenides as thermoelectric materials. J. Solid State Chem. 2019, 270, 273–279. [Google Scholar] [CrossRef]
- Yu, Y.; Cagnoni, M.; Cojocaru-Mirédin, O.; Wuttig, M. Chalcogenide Thermoelectrics Empowered by an Unconventional Bonding Mechanism. Adv. Funct. Mater. 2020, 30, 1904862. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.D.; Lo, S.H.; Zhang, Y.; Sun, H.; Tan, G.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 2014, 508, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.D.; Tan, G.; Hao, S.; He, J.; Pei, Y.; Chi, H.; Wang, H.; Gong, S.; Xu, H.; Dravid, V.P.; et al. Ultrahigh power factor and thermoelectric performance in hole-doped single-crystal SnSe. Science 2016, 351, 141–144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sinsermsuksakul, P.; Sun, L.; Lee, S.W.; Park, H.H.; Kim, S.B.; Yang, C.; Gordon, R.G. Overcoming Efficiency Limitations of SnS-Based Solar Cells. Adv. Energy Mater. 2014, 4, 1400496. [Google Scholar] [CrossRef]
- Yun, H.S.; Park, B.w.; Choi, Y.C.; Im, J.; Shin, T.J.; Seok, S.I. Efficient Nanostructured TiO2/SnS Heterojunction Solar Cells. Adv. Energy Mater. 2019, 9, 1901343. [Google Scholar] [CrossRef]
- Cho, J.Y.; Kim, S.; Nandi, R.; Jang, J.; Yun, H.S.; Enkhbayar, E.; Kim, J.H.; Lee, D.K.; Chung, C.H.; Kim, J.; et al. Achieving over 4% efficiency for SnS/CdS thin-film solar cells by improving the heterojunction interface quality. J. Mater. Chem. A 2020, 8, 20658–20665. [Google Scholar] [CrossRef]
- Abd El-Rahman, K.; Darwish, A.; El-Shazly, E. Electrical and photovoltaic properties of SnSe/Si heterojunction. Mater. Sci. Semicond. Process. 2014, 25, 123–129. [Google Scholar] [CrossRef]
- Shi, W.; Gao, M.; Wei, J.; Gao, J.; Fan, C.; Ashalley, E.; Li, H.; Wang, Z. Tin Selenide (SnSe): Growth, Properties, and Applications. Adv. Sci. 2018, 5, 1700602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ouyang, B.; Chang, C.; Zhao, L.D.; Wang, Z.L.; Yang, Y. Thermo-photoelectric coupled effect induced electricity in N-type SnSe:Br single crystals for enhanced self-powered photodetectors. Nano Energy 2019, 66, 104111. [Google Scholar] [CrossRef]
- Xu, H.; Hao, L.; Liu, H.; Dong, S.; Wu, Y.; Liu, Y.; Cao, B.; Wang, Z.; Ling, C.; Li, S.; et al. Flexible SnSe Photodetectors with Ultrabroad Spectral Response up to 10.6 μm Enabled by Photobolometric Effect. ACS Appl. Mater. Interfaces 2020, 12, 35250–35258. [Google Scholar] [CrossRef]
- Chattopadhyay, T.; Pannetier, J.; Von Schnering, H.G. Neutron diffraction study of the structural phase transition in SnS and SnSe. J. Phys. Chem. Solids 1986, 47, 879–885. [Google Scholar] [CrossRef]
- Skelton, J.M.; Burton, L.A.; Parker, S.C.; Walsh, A.; Kim, C.E.; Soon, A.; Buckeridge, J.; Sokol, A.A.; Catlow, C.R.A.; Togo, A.; et al. Anharmonicity in the High-Temperature Cmcm Phase of SnSe: Soft Modes and Three-Phonon Interactions. Phys. Rev. Lett. 2016, 117, 075502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heremans, J.P. The ugly duckling. Nature 2014, 508, 327–328. [Google Scholar] [CrossRef]
- Tan, Q.; Zhao, L.D.; Li, J.F.; Wu, C.F.; Wei, T.R.; Xing, Z.B.; Kanatzidis, M.G. Thermoelectrics with earth abundant elements: Low thermal conductivity and high thermopower in doped SnS. J. Mater. Chem. A 2014, 2, 17302–17306. [Google Scholar] [CrossRef]
- Zhou, B.; Li, S.; Li, W.; Li, J.; Zhang, X.; Lin, S.; Chen, Z.; Pei, Y. Thermoelectric Properties of SnS with Na-Doping. ACS Appl. Mater. Interfaces 2017, 9, 34033–34041. [Google Scholar] [CrossRef]
- Cai, B.; Zhao, L.D.; Li, J.F. High thermoelectric figure of merit ZT > 1 in SnS polycrystals. J. Mater. 2020, 6, 77–85. [Google Scholar] [CrossRef]
- Han, Y.M.; Zhao, J.; Zhou, M.; Jiang, X.X.; Leng, H.Q.; Li, L.F. Thermoelectric performance of SnS and SnS–SnSe solid solution. J. Mater. Chem. A 2015, 3, 4555–4559. [Google Scholar] [CrossRef]
- Wei, T.R.; Li, Z.; Sun, F.H.; Pan, Y.; Wu, C.F.; Farooq, M.U.; Tang, H.; Li, F.; Li, B.; Li, J.F. Thermoelectric SnS and SnS-SnSe solid solutions prepared by mechanical alloying and spark plasma sintering: Anisotropic thermoelectric properties. Sci. Rep. 2017, 7, 43262. [Google Scholar] [CrossRef]
- Lin, C.C.; Lydia, R.; Yun, J.H.; Lee, H.S.; Rhyee, J.S. Extremely Low Lattice Thermal Conductivity and Point Defect Scattering of Phonons in Ag-doped (SnSe)1−x(SnS)x Compounds. Chem. Mater. 2017, 29, 5344–5352. [Google Scholar] [CrossRef]
- Mariano, A.N.; Chopra, K.L. Polymorphism In Some IV–VI Compounds Induced By High Pressure And Thin-Film Epitaxial Growth. Appl. Phys. Lett. 1967, 10, 282–284. [Google Scholar] [CrossRef]
- Bilenkii, B.F.; Mikolaichuk, A.G.; Freik, D.M. Struktur und optische Eigenschaften von epitaxialen SnTe-, SnSe- und SnS-Schichten. Phys. Status Solidi B 1968, 28, K5–K7. [Google Scholar] [CrossRef]
- Greyson, E.; Barton, J.; Odom, T. Tetrahedral Zinc Blende Tin Sulfide Nano- and Microcrystals. Small 2006, 2, 368–371. [Google Scholar] [CrossRef] [PubMed]
- Ahmet, I.Y.; Hill, M.S.; Johnson, A.L.; Peter, L.M. Polymorph-Selective Deposition of High Purity SnS Thin Films from a Single Source Precursor. Chem. Mater. 2015, 27, 7680–7688. [Google Scholar] [CrossRef] [Green Version]
- Rabkin, A.; Samuha, S.; Abutbul, R.E.; Ezersky, V.; Meshi, L.; Golan, Y. New Nanocrystalline Materials: A Previously Unknown Simple Cubic Phase in the SnS Binary System. Nano Lett. 2015, 15, 2174–2179. [Google Scholar] [CrossRef] [PubMed]
- Abutbul, R.E.; Garcia-Angelmo, A.R.; Burshtein, Z.; Nair, M.T.S.; Nair, P.K.; Golan, Y. Crystal structure of a large cubic tin monosulfide polymorph: An unraveled puzzle. CrystEngComm 2016, 18, 5188–5194. [Google Scholar] [CrossRef] [Green Version]
- Abutbul, R.E.; Segev, E.; Samuha, S.; Zeiri, L.; Ezersky, V.; Makov, G.; Golan, Y. A new nanocrystalline binary phase: Synthesis and properties of cubic tin monoselenide. CrystEngComm 2016, 18, 1918–1923. [Google Scholar] [CrossRef] [Green Version]
- Skelton, J.M.; Burton, L.A.; Oba, F.; Walsh, A. Chemical and Lattice Stability of the Tin Sulfides. J. Phys. Chem. C 2017, 121, 6446–6454. [Google Scholar] [CrossRef] [PubMed]
- Pallikara, I.; Skelton, J.M. Phase stability of the tin monochalcogenides SnS and SnSe: A quasi-harmonic lattice dynamics study. Phys. Chem. Chem. Phys. 2021, 23, 19219–19236. [Google Scholar] [CrossRef]
- Xie, Y.; Zhou, Y.; Gong, X.G. The intrinsic low lattice thermal conductivity in the rock salt SnSe. Comput. Mater. Sci. 2018, 148, 54–59. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Ganose, A.M.; Park, J.; Faghaninia, A.; Woods-Robinson, R.; Persson, K.A.; Jain, A. Efficient calculation of carrier scattering rates from first principles. Nat. Commun. 2021, 12, 2222. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Gajdoš, M. and Hummer, K. and Kresse, G. and Furthmüller, J.; Bechstedt, F.. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 2006, 73, 045112. [Google Scholar] [CrossRef] [Green Version]
- Porezag, D.; Pederson, M.R. Infrared intensities and Raman-scattering activities within density-functional theory. Phys. Rev. B 1996, 54, 7830–7836. [Google Scholar] [CrossRef]
- Nunes, R.W.; Gonze, X. Berry-phase treatment of the homogeneous electric field perturbation in insulators. Phys. Rev. B 2001, 63, 155107. [Google Scholar] [CrossRef] [Green Version]
- Souza, I.; Íñiguez, J.; Vanderbilt, D. First-Principles Approach to Insulators in Finite Electric Fields. Phys. Rev. Lett. 2002, 89, 117602. [Google Scholar] [CrossRef] [Green Version]
- Togo, A.; Chaput, L.; Tanaka, I. Distributions of phonon lifetimes in Brillouin zones. Phys. Rev. B 2015, 91, 094306. [Google Scholar] [CrossRef] [Green Version]
- Skelton, J.M. Approximate models for the lattice thermal conductivity of alloy thermoelectrics. J. Mater. Chem. C 2021, 9, 11772–11787. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Lu, Y.; Zheng, F.w.; Yang, Y.; Zhang, P.; Zhang, D.B. Phase stabilities of Cmcm and Pnma SnSe studied by phonon quasiparticle approach. Phys. Rev. B 2019, 100, 054304. [Google Scholar] [CrossRef]
- Walsh, A.; Payne, D.J.; Egdell, R.G.; Watson, G.W. Stereochemistry of post-transition metal oxides: Revision of the classical lone pair model. Chem. Soc. Rev. 2011, 40, 4455–4463. [Google Scholar] [CrossRef] [Green Version]
- Whittles, T.J.; Burton, L.A.; Skelton, J.M.; Walsh, A.; Veal, T.D.; Dhanak, V.R. Band Alignments, Valence Bands, and Core Levels in the Tin Sulfides SnS, SnS2, and Sn2S3: Experiment and Theory. Chem. Mater. 2016, 28, 3718–3726. [Google Scholar] [CrossRef] [Green Version]
- Skelton, J.M.; Parker, S.C.; Togo, A.; Tanaka, I.; Walsh, A. Thermal physics of the lead chalcogenides PbS, PbSe, and PbTe from first principles. Phys. Rev. B 2014, 89, 205203. [Google Scholar] [CrossRef] [Green Version]
- Madsen, G.K.; Carrete, J.; Verstraete, M.J. BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comput. Phys. Commun. 2018, 231, 140–145. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Lee, Y.K.; Yu, Y.; Byun, S.; Luo, Z.Z.; Lee, H.; Ge, B.; Lee, Y.L.; Chen, X.; Lee, J.Y.; et al. Polycrystalline SnSe with a thermoelectric figure of merit greater than the single crystal. Nat. Mater. 2021, 20, 1378–1384. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.D.; Chang, C.; Tan, G.; Kanatzidis, M.G. SnSe: A remarkable new thermoelectric material. Energy Environ. Sci. 2016, 9, 3044–3060. [Google Scholar] [CrossRef]
- Skelton, J.M.; Tiana, D.; Parker, S.C.; Togo, A.; Tanaka, I.; Walsh, A. Influence of the exchange-correlation functional on the quasi-harmonic lattice dynamics of II-VI semiconductors. J. Chem. Phys. 2015, 143, 064710. [Google Scholar] [CrossRef] [Green Version]
- Božin, E.S.; Malliakas, C.D.; Souvatzis, P.; Proffen, T.; Spaldin, N.A.; Kanatzidis, M.G.; Billinge, S.J.L. Entropically Stabilized Local Dipole Formation in Lead Chalcogenides. Science 2010, 330, 1660–1663. [Google Scholar] [CrossRef] [PubMed]
- Kastbjerg, S.; Bindzus, N.; Søndergaard, M.; Johnsen, S.; Lock, N.; Christensen, M.; Takata, M.; Spackman, M.A.; Brummerstedt Iversen, B. Direct Evidence of Cation Disorder in Thermoelectric Lead Chalcogenides PbTe and PbS. Adv. Funct. Mater. 2013, 23, 5477–5483. [Google Scholar] [CrossRef]
- Keiber, T.; Bridges, F.; Sales, B.C. Lead Is Not Off Center in PbTe: The Importance of r-Space Phase Information in Extended X-Ray Absorption Fine Structure Spectroscopy. Phys. Rev. Lett. 2013, 111, 095504. [Google Scholar] [CrossRef] [Green Version]
- Knight, K.S. A high-resolution neutron powder diffraction investigation of galena PbS between 10 K and 350 K: No evidence for anomalies in the lattice parameters or atomic displacement parameters in galena or altaite PbTe at temperatures corresponding to the saturation of cation disorder. J. Physics Condens. Matter. 2014, 26, 385403. [Google Scholar] [CrossRef]
- Tang, J.; Skelton, J.M. Impact of noble-gas filler atoms on the lattice thermal conductivity of CoSb3 skutterudites: First-principles modelling. J. Phys. Condens. Matter. 2021, 33, 164002. [Google Scholar] [CrossRef] [PubMed]
- Skelton, J.M.; Burton, L.A.; Jackson, A.J.; Oba, F.; Parker, S.C.; Walsh, A. Lattice dynamics of the tin sulphides SnS2, SnS and Sn2S3: Vibrational spectra and thermal transport. Phys. Chem. Chem. Phys. 2017, 19, 12452–12465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
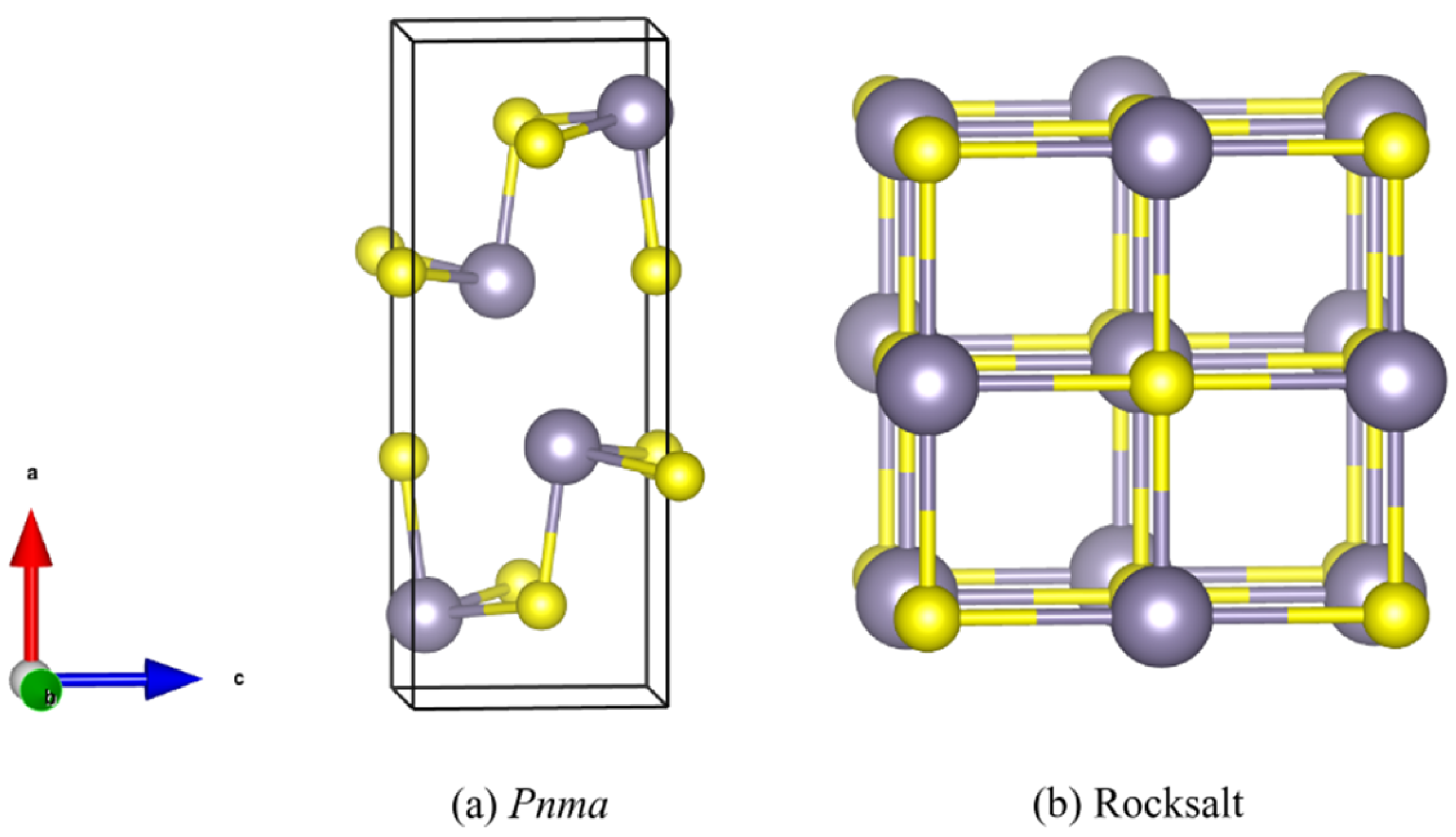
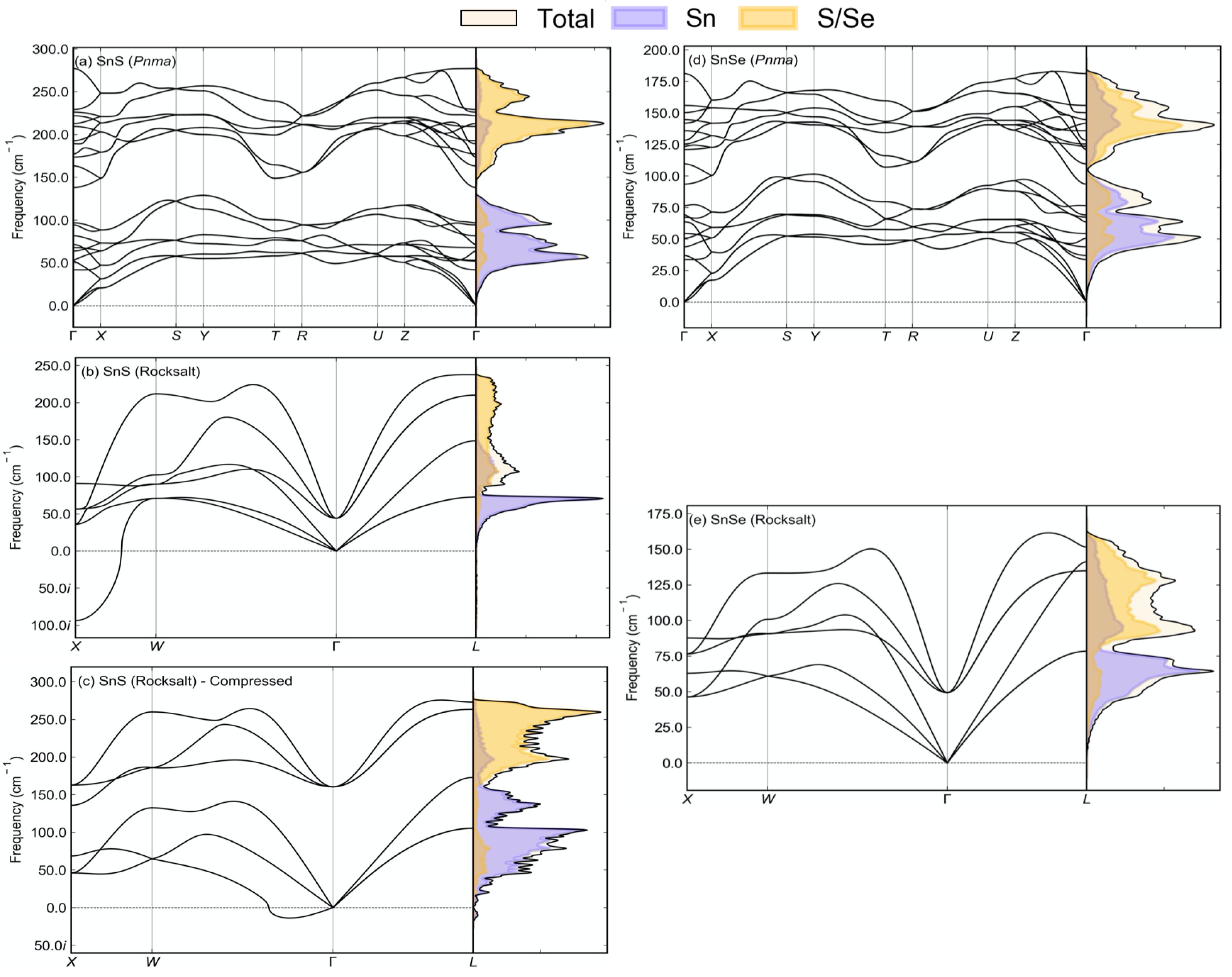
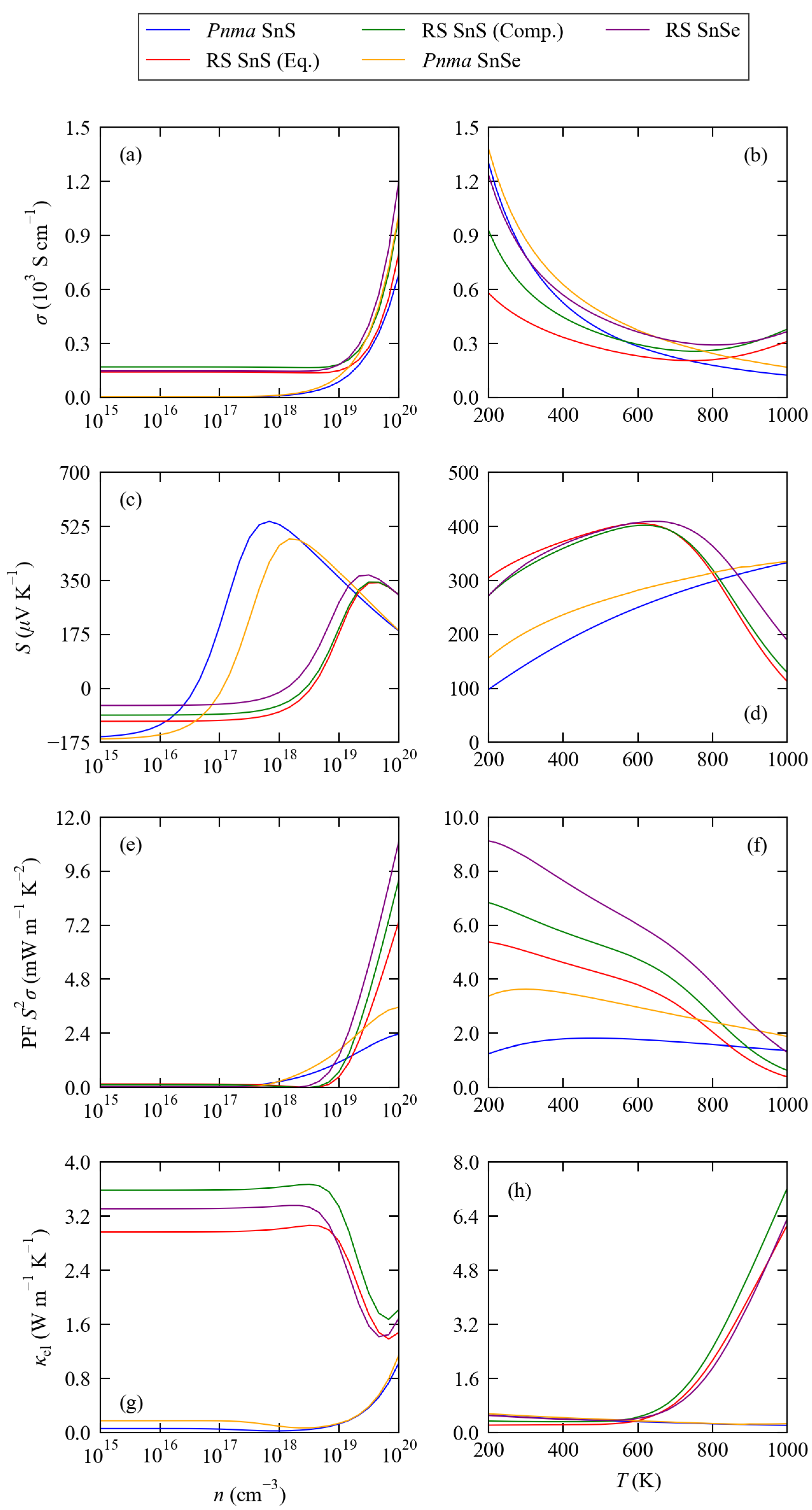
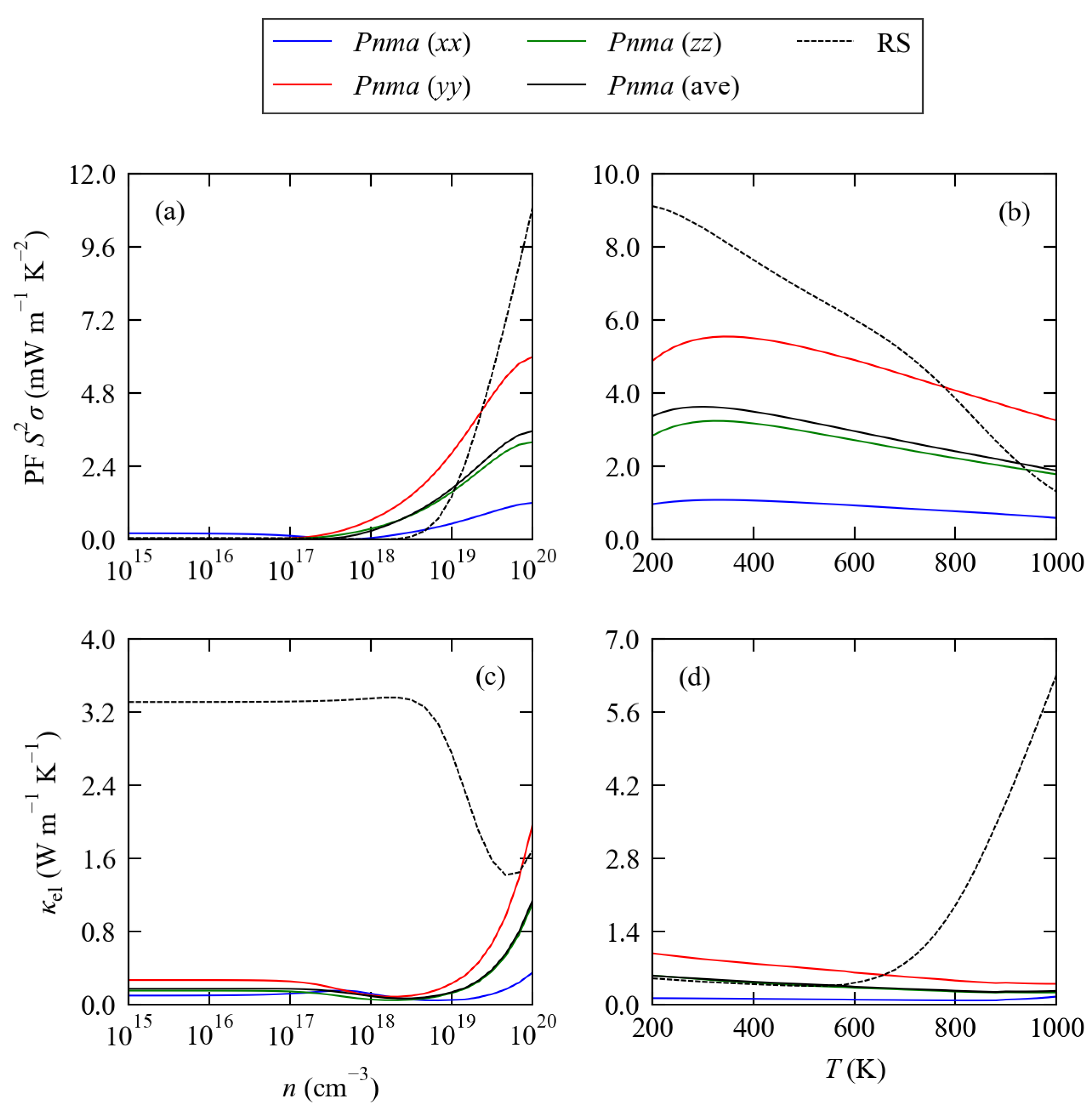


| a (Å) | b (Å) | c (Å) | V (Å3) | |
|---|---|---|---|---|
| SnS (Pnma) | 11.000 | 3.965 | 4.202 | 183.2 |
| SnS (RS, Eq.) | 5.712 | - | - | 186.3 |
| SnS (RS, Comp.) | 5.426 | - | - | 159.8 |
| SnSe (Pnma) | 11.350 | 4.124 | 4.335 | 202.9 |
| SnSe (RS) | 5.912 | - | - | 206.7 |
| (W m−1 K−1) | ||||||
|---|---|---|---|---|---|---|
| (W m−1 K−1 ps−1) | (ps) | |||||
| SnS (Pnma) | 0.508 | 1.196 | 0.708 | 0.804 | 0.755 | 1.065 |
| SnS (RS, Eq.) | 0.606 | - | - | 0.606 | 7.699 | 0.079 |
| SnS (RS, Comp.) | 3.142 | - | - | 3.142 | 5.512 | 0.570 |
| SnSe (Pnma) | 0.354 | 0.814 | 0.613 | 0.593 | 0.380 | 1.561 |
| SnSe (RS) | 1.665 | - | - | 1.665 | 1.578 | 1.055 |
| n | T | S | PF | (W m−1 K−1) | |||||
|---|---|---|---|---|---|---|---|---|---|
| (cm−3) | (K) | (S cm−1) | (V K−1) | (mW m−1 K−2) | |||||
| SnS (Pnma) | 4.64 × 10 | 1000 | 1.75 | 252 | 272 | 1.87 | 0.43 | 0.64 | 1.07 |
| SnS (RS, Eq.) | 10 | 720 | 2.99 | 885 | 297 | 7.84 | 1.22 | 0.49 | 1.70 |
| SnS (RS, Comp.) | 10 | 800 | 1.48 | 999 | 303 | 9.19 | 1.82 | 2.51 | 4.33 |
| SnSe (Pnma) | 4.64 × 10 | 1000 | 2.81 | 348 | 274 | 2.62 | 0.46 | 0.47 | 0.93 |
| SnSe (RS) | 10 | 800 | 2.60 | 1196 | 302 | 10.90 | 1.69 | 1.33 | 3.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flitcroft, J.M.; Pallikara, I.; Skelton, J.M. Thermoelectric Properties of Pnma and Rocksalt SnS and SnSe. Solids 2022, 3, 155-176. https://doi.org/10.3390/solids3010011
Flitcroft JM, Pallikara I, Skelton JM. Thermoelectric Properties of Pnma and Rocksalt SnS and SnSe. Solids. 2022; 3(1):155-176. https://doi.org/10.3390/solids3010011
Chicago/Turabian StyleFlitcroft, Joseph M., Ioanna Pallikara, and Jonathan M. Skelton. 2022. "Thermoelectric Properties of Pnma and Rocksalt SnS and SnSe" Solids 3, no. 1: 155-176. https://doi.org/10.3390/solids3010011
APA StyleFlitcroft, J. M., Pallikara, I., & Skelton, J. M. (2022). Thermoelectric Properties of Pnma and Rocksalt SnS and SnSe. Solids, 3(1), 155-176. https://doi.org/10.3390/solids3010011








