Migration Barrier Estimation of Carbon in Lead for Lead–Acid Battery Applications: A Density Functional Theory Approach
Abstract
:1. Introduction
2. Computational Details
Density Functional Theory
3. Results and Discussion
3.1. Validation and Selection of Functional for Pb
3.2. Carbon Placement in the Pb Matrix
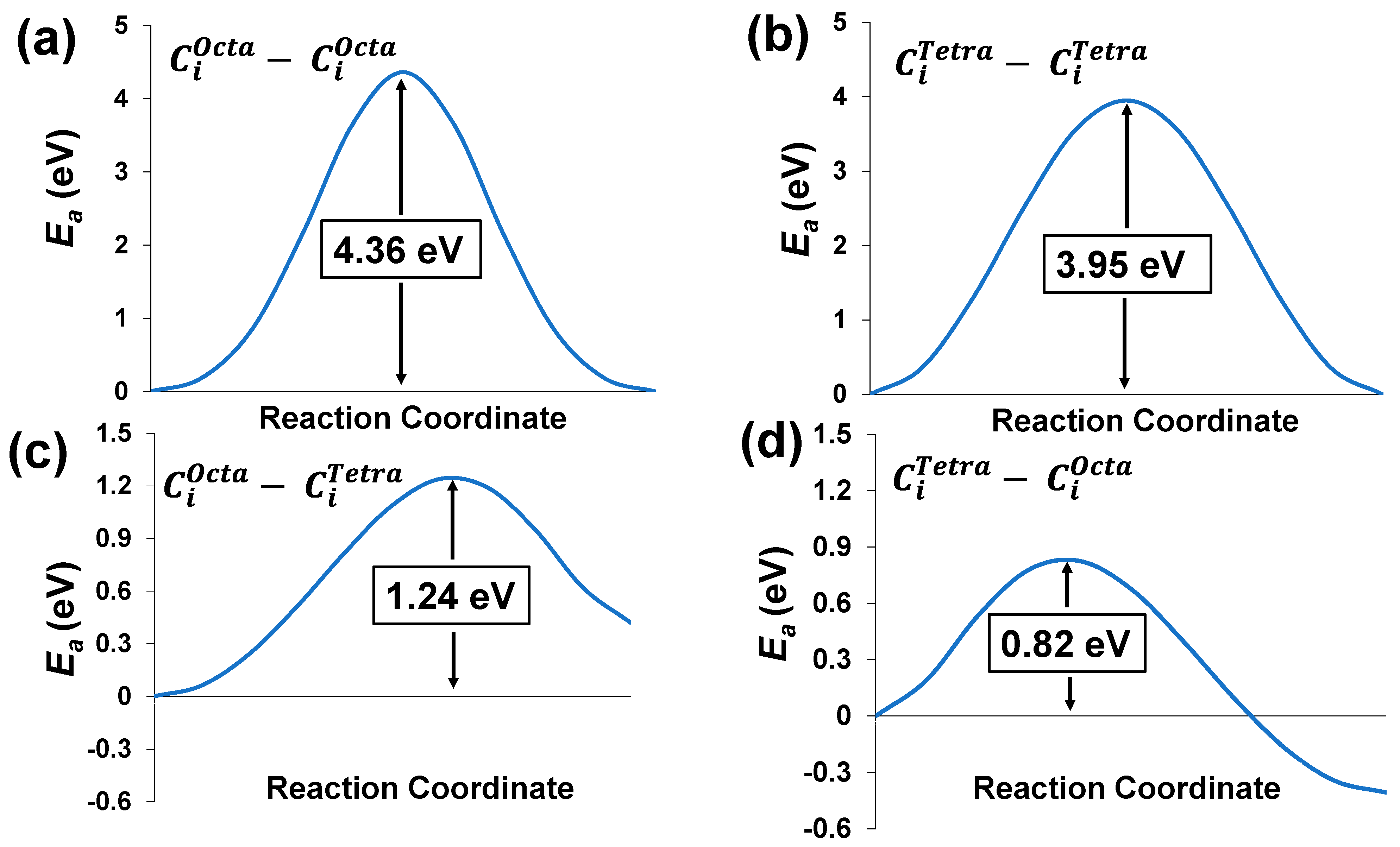
3.3. Activation Barrier for C Diffusion in the Pb Matrix
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grothoff, J.M. Battery storage for renewables: Market status and technology outlook. Int. Renew. Energy Agency Abu Dhabi 2015, 32, 6–10. [Google Scholar]
- Gaddam, R.R.; Katzenmeier, L.; Lamprecht, X.; Bandarenka, A.S. Review on physical impedance models in modern battery research. Phys. Chem. Chem. Phys. 2021, 23, 12926–12944. [Google Scholar] [CrossRef] [PubMed]
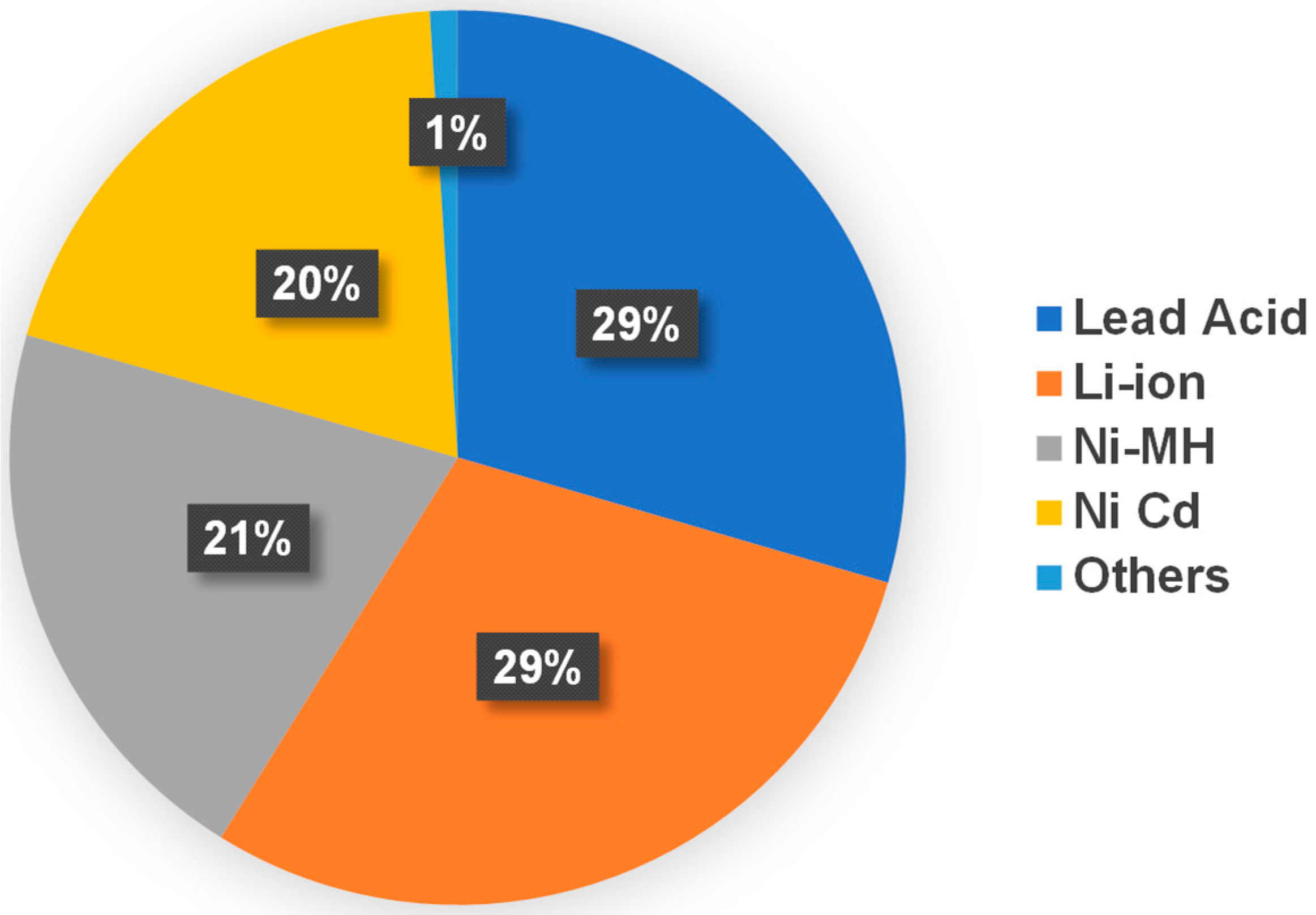
- Grand View Research. Battery Market Size, Share & Trends Analysis Report by Product (Lead Acid, Li-ion, Nickle Metal Hydride, Ni-cd), By Application (Automotive, Industrial, Portable), By Region, And Segment Forecasts, 2020–2027. Available online: https://www.grandviewresearch.com/industry-analysis/battery-market (accessed on 12 December 2020).
- Tran, M.-K.; DaCosta, A.; Mevawalla, A.; Panchal, S.; Fowler, M. Comparative Study of Equivalent Circuit Models Performance in Four Common Lithium-Ion Batteries: LFP, NMC, LMO, NCA. Batteries 2021, 7, 51. [Google Scholar] [CrossRef]
- Samanta, B.K.; Samanta, H.; Deb, N.K.; Saha, H. Battery Storage Technologies: A Review. Intell. Electr. Syst. 2021, 257–268. [Google Scholar]
- Armand, M.; Tarascon, J.-M. Building better batteries. Nature 2008, 451, 652–657. [Google Scholar] [CrossRef]
- Manthiram, A. A reflection on lithium-ion battery cathode chemistry. Nat. Commun. 2020, 11, 1550. [Google Scholar] [CrossRef]
- Keshan, H.; Thornburg, J.; Ustun, T.S. Comparison of lead-acid and lithium ion batteries for stationary storage in off-grid energy systems. In Proceedings of the 4th IET Clean Energy and Technology Conference (CEAT 2016), Kuala Lumpur, Malaysia, 14–15 November 2016. [Google Scholar]
- Podder, S.; Khan, M.Z.R. Comparison of lead acid and Li-ion battery in solar home system of Bangladesh. In Proceedings of the 5th International Conference on Informatics, Electronics and Vision (ICIEV), Dhaka, Bangladesh, 13–14 May 2016; pp. 434–438. [Google Scholar]
- Daoud, A.; Abou El-Khair, M.T.; Shenouda, A.Y.; Fairouz, F.; Mohamed, E.; Abdel Aziz, M.E.; Yanamandra, K.; Gupta, N. Novel Pb alloys based composite foams containing hybrid pores produced by liquid metallurgy for lightweight batteries. Int. J. Lightweight Mater. Manuf. 2022, 5, 44–57. [Google Scholar] [CrossRef]
- Daoud, A.; Abou El-Khair, M.T.; Shenouda, A.Y.; Fairouz, F.; Mohamed, E.; Abdel Aziz, M.E.; Yanamandra, K.; Gupta, N. Aging behavior and thermal expansion of novel Pb alloys reinforced with fly ash cenospheres composite foams. Int. J. Lightweight Mater. Manuf. 2022, 5, 178–187. [Google Scholar] [CrossRef]
- Pavlov, D.; Rogachev, T.; Nikolov, P.; Petkova, G. Mechanism of action of electrochemically active carbons on the processes that take place at the negative plates of lead-acid batteries. J. Power Sources 2009, 191, 58–75. [Google Scholar] [CrossRef]
- Pavlov, D.; Nikolov, P.; Rogachev, T. Influence of carbons on the structure of the negative active material of lead-acid batteries and on battery performance. J. Power Sources 2011, 196, 5155–5167. [Google Scholar] [CrossRef]
- Zhang, W.; Lin, H.; Lu, H.; Liu, D.; Yin, J.; Lin, Z. On the electrochemical origin of the enhanced charge acceptance of the lead–carbon electrode. J. Mater. Chem. A 2015, 3, 4399–4404. [Google Scholar] [CrossRef]
- Yang, H.; Qiu, Y.; Guo, X. Lead oxide/carbon black composites prepared with a new pyrolysis-pickling method and their effects on the high-rate partial-state-of-charge performance of lead-acid batteries. Electrochim. Acta 2017, 235, 409–421. [Google Scholar] [CrossRef]
- Yanamandra, K.; Pinisetty, D.; Daoud, A.; Gupta, N. Recycling of Li-Ion and Lead Acid Batteries: A Review. J. Indian Inst. Sci. 2022. [Google Scholar] [CrossRef]
- Pavlov, D.; Nikolov, P. Lead–carbon electrode with inhibitor of sulfation for lead-acid batteries operating in the HRPSoC duty. J. Electrochem. Soc. 2012, 159, A1215. [Google Scholar] [CrossRef]
- Xiang, J.; Ding, P.; Zhang, H.; Wu, X.; Chen, J.; Yang, Y. Beneficial effects of activated carbon additives on the performance of negative lead-acid battery electrode for high-rate partial-state-of-charge operation. J. Power Sources 2013, 241, 150–158. [Google Scholar] [CrossRef]
- Yin, J.; Lin, N.; Zhang, W.; Lin, Z.; Zhang, Z.; Wang, Y.; Shi, J.; Bao, J.; Lin, H. Highly reversible lead-carbon battery anode with lead grafting on the carbon surface. J. Energy Chem. 2018, 27, 1674–1683. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.-L.; Yin, J.; Lin, Z.-Q.; Shi, J.; Wang, C.; Liu, D.-B.; Wang, Y.; Bao, J.-P.; Lin, H.-B. Lead-carbon electrode designed for renewable energy storage with superior performance in partial state of charge operation. J. Power Sources 2017, 342, 183–191. [Google Scholar] [CrossRef]
- Moseley, P.T. Consequences of including carbon in the negative plates of Valve-regulated Lead–Acid batteries exposed to high-rate partial-state-of-charge operation. J. Power Sources 2009, 191, 134–138. [Google Scholar] [CrossRef]
- Pavlov, D.; Nikolov, P. Capacitive carbon and electrochemical lead electrode systems at the negative plates of lead–acid batteries and elementary processes on cycling. J. Power Sources 2013, 242, 380–399. [Google Scholar] [CrossRef]
- Fernández, M.; Valenciano, J.; Trinidad, F.; Muñoz, N. The use of activated carbon and graphite for the development of lead-acid batteries for hybrid vehicle applications. J. Power Sources 2010, 195, 4458–4469. [Google Scholar] [CrossRef]
- Saravanan, M.; Ganesan, M.; Ambalavanan, S. A modified lead-acid negative electrode for high-rate partial-state-of-charge applications. J. Electrochem. Soc. 2012, 159, A452. [Google Scholar] [CrossRef]
- Zou, X.; Kang, Z.; Shu, D.; Liao, Y.; Gong, Y.; He, C.; Hao, J.; Zhong, Y. Effects of carbon additives on the performance of negative electrode of lead-carbon battery. Electrochim. Acta 2015, 151, 89–98. [Google Scholar] [CrossRef]
- Kumar, S.M.; Ambalavanan, S.; Mayavan, S. Effect of graphene and carbon nanotubes on the negative active materials of lead acid batteries operating under high-rate partial-state-of-charge operation. RSC Adv. 2014, 4, 36517–36521. [Google Scholar] [CrossRef]
- Geetha, A.; Subramani, C. A comprehensive review on energy management strategies of hybrid energy storage system for electric vehicles. Int. J. Energy Res. 2017, 41, 1817–1834. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, G.; Yue, X.; Wang, D. Study of graphene as a negative additive for valve-regulated lead-acid batteries working under high-rate partial-state-of-charge conditions. Int. J. Electrochem. Sci. 2016, 11, 700–709. [Google Scholar]
- Mahajan, V.; Bharj, R.S.; Bharj, J. Role of nano-carbon additives in lead-acid batteries: A review. Bull. Mater. Sci. 2019, 42, 21. [Google Scholar] [CrossRef] [Green Version]
- Saravanan, M.; Sennu, P.; Ganesan, M.; Ambalavanan, S. Multi-walled carbon nanotubes percolation network enhanced the performance of negative electrode for lead-acid battery. J. Electrochem. Soc. 2012, 160, A70. [Google Scholar] [CrossRef] [Green Version]
- Swogger, S.W.; Everill, P.; Dubey, D.; Sugumaran, N. Discrete carbon nanotubes increase lead acid battery charge acceptance and performance. J. Power Sources 2014, 261, 55–63. [Google Scholar] [CrossRef] [Green Version]
- Yin, J.; Lin, N.; Lin, Z.-Q.; Wang, Y.; Shi, J.; Bao, J.-P.; Lin, H.-B.; Feng, S.-H.; Zhang, W.-L. Towards renewable energy storage: Understanding the roles of rice husk-based hierarchical porous carbon in the negative electrode of lead-carbon battery. J. Energy Storage 2019, 24, 100756. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, W.; Lin, H.; Li, Y.; Lu, H.; Wang, Y. A green technology for the preparation of high capacitance rice husk-based activated carbon. J. Clean. Prod. 2016, 112, 1190–1198. [Google Scholar] [CrossRef]
- Åvall, G.; Mindemark, J.; Brandell, D.; Johansson, P. Sodium-Ion Battery Electrolytes: Modeling and Simulations. Adv. Energy Mater. 2018, 8, 1703036. [Google Scholar] [CrossRef]
- Bai, Q.; Yang, L.; Chen, H.; Mo, Y. Computational studies of electrode materials in sodium-ion batteries. Adv. Energy Mater. 2018, 8, 1702998. [Google Scholar] [CrossRef]
- Chen, X.; Hou, T.; Persson, K.A.; Zhang, Q. Combining theory and experiment in lithium–sulfur batteries: Current progress and future perspectives. Mater. Today 2019, 22, 142–158. [Google Scholar] [CrossRef]
- Chakraborty, S.; Banerjee, A.; Watcharatharapong, T.; Araujo, R.B.; Ahuja, R. Current computational trends in polyanionic cathode materials for Li and Na batteries. J. Phys. Condens. Matter 2018, 30, 283003. [Google Scholar] [CrossRef]
- Wasalathilake, K.C.; Ayoko, G.A.; Yan, C. Effects of heteroatom doping on the performance of graphene in sodium-ion batteries: A density functional theory investigation. Carbon 2018, 140, 276–285. [Google Scholar] [CrossRef]
- Lee, H.W.; Moon, H.S.; Hur, J.; Kim, I.T.; Park, M.S.; Yun, J.M.; Kim, K.H.; Lee, S.G. Mechanism of sodium adsorption on N-doped graphene nanoribbons for sodium ion battery applications: A density functional theory approach. Carbon 2017, 119, 492–501. [Google Scholar] [CrossRef]
- Sulzer, V.; Chapman, S.J.; Please, C.P.; Howey, D.A.; Monroe, C.W. Faster Lead-Acid Battery Simulations from Porous-Electrode Theory: Part I. Physical Model. J. Electrochem. Soc. 2019, 166, A2363–A2371. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Materials Design Inc. MedeA Version 3.0; MedeA is a Registered Trademark of Materials Design; MedeA: San Diego, CA, USA, 2022; Available online: https://www.materialsdesign.com/medea-software (accessed on 24 January 2022).
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Phys rev lett 77: 3865. Errata 1996, 78, 1396. [Google Scholar]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Walker, G.; Marezio, M. Lattice parameters and zone overlap in solid solutions of lead in magnesium. Acta Metall. 1959, 7, 769–773. [Google Scholar] [CrossRef]
- Papaconstantopoulos, D.A.; Mehl, M.J. Tight-Binding Method in Electronic Structure. In Encyclopedia of Condensed Matter Physics; Bassani, F., Liedl, G.L., Wyder, P., Eds.; Elsevier: Oxford, UK, 2005; pp. 194–206. [Google Scholar] [CrossRef]
- Lejaeghere, K.; Van Speybroeck, V.; Van Oost, G.; Cottenier, S. Error Estimates for Solid-State Density-Functional Theory Predictions: An Overview by Means of the Ground-State Elemental Crystals. Crit. Rev. Solid State Mater. Sci. 2014, 39, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Shang, S.L.; Saengdeejing, A.; Mei, Z.G.; Kim, D.E.; Zhang, H.; Ganeshan, S.; Wang, Y.; Liu, Z.K. First-principles calculations of pure elements: Equations of state and elastic stiffness constants. Comput. Mater. Sci. 2010, 48, 813–826. [Google Scholar] [CrossRef]
- The Materials Project. Materials Explorer—Pb. Available online: https://next-gen.materialsproject.org/materials/mp-20483/# (accessed on 24 January 2022).
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef] [Green Version]
- Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 1980, 45, 566. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Armiento, R.; Mattsson, A.E. Functional designed to include surface effects in self-consistent density functional theory. Phys. Rev. B 2005, 72, 085108. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [Green Version]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef] [Green Version]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef] [Green Version]
- Villars, P.; Daams, J.L.C. Atomic-environment classification of the chemical elements. J. Alloys Compd. 1993, 197, 177–196. [Google Scholar] [CrossRef]
- Simmons, G. Single Crystal Elastic Constants and Calculated Aggregate Properties; Southern Methodist University: Dallas, TX, USA, 1965. [Google Scholar]
- Jiang, D.E.; Carter, E.A. Carbon dissolution and diffusion in ferrite and austenite from first principles. Phys. Rev. B 2003, 67, 214103. [Google Scholar] [CrossRef] [Green Version]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef] [Green Version]
- Urban, A.; Seo, D.-H.; Ceder, G. Computational understanding of Li-ion batteries. Npj Comput. Mater. 2016, 2, 16002. [Google Scholar] [CrossRef]
- Van der Ven, A.; Bhattacharya, J.; Belak, A.A. Understanding Li Diffusion in Li-Intercalation Compounds. Acc. Chem. Res. 2013, 46, 1216–1225. [Google Scholar] [CrossRef]
- Yang, J.; Hu, C.; Wang, H.; Yang, K.; Liu, J.B.; Yan, H. Review on the Research of Failure Modes and Mechanism for Lead–Acid Batteries. Int. J. Energy Res. 2017, 41, 336–352. [Google Scholar] [CrossRef]


| Supercell Size (X × Y × Z) | Number of Pb Atoms | Number of C Atoms | at% of C in the Supercell | wt% of C in the Supercell |
|---|---|---|---|---|
| 1 × 1 × 1 | 4 | 1 | 20.00 | 1.43 |
| 2 × 1 × 1 | 8 | 1 | 11.11 | 0.72 |
| 2 × 2 × 1 | 16 | 1 | 5.88 | 0.36 |
| 2 × 2 × 2 | 32 | 1 | 3.03 | 0.18 |
| Data Source | Crystal Structure Related | Elastic Stiffness (Cij) and Bulk Modulus (B) | |||||
|---|---|---|---|---|---|---|---|
| a (Å) | α (°) | Volume (Å3) | C11 (GPa) | C12 (GPa) | C44 (GPa) | B (GPa) | |
| Experiment | 4.9508 | 90.00 | 121.36 | 55.54 # 47.65 † | 45.42 # 40.28 † | 19.42 # 14.41 † | 48.79 #,* 42.73 †,* |
| LDA | 4.8798 | 90.00 | 116.20 | 58.03 | 44.67 | 18.92 | 49.12 |
| GGA-PBE | 5.0319 | 90.00 | 127.41 | 46.04 | 34.04 | 15.59 | 38.04 |
| GGA-AM05 | 4.9360 | 90.00 | 120.26 | 53.45 | 43.33 | −17.46 | 46.70 |
| GGA-PBESol | 4.9265 | 90.00 | 119.57 | 53.88 | 40.61 | 18.36 | 45.03 |
| GGA-rPBE | 5.0987 | 90.00 | 132.55 | 40.86 | 29.42 | 14.05 | 33.23 |
| GGA-BLYP | 5.1730 | 90.00 | 138.43 | 36.77 | 27.55 | 10.46 | 30.62 |
| HSE06 | 4.9645 | 90.00 | 122.36 | 42.25 | 34.15 | −16.25 | 36.85 |
| PBE0 | 4.9598 | 90.00 | 122.01 | 43.83 | 34.11 | −15.77 | 37.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yanamandra, K.; Behera, R.K.; Daoud, A.; Gupta, N. Migration Barrier Estimation of Carbon in Lead for Lead–Acid Battery Applications: A Density Functional Theory Approach. Solids 2022, 3, 177-187. https://doi.org/10.3390/solids3020012
Yanamandra K, Behera RK, Daoud A, Gupta N. Migration Barrier Estimation of Carbon in Lead for Lead–Acid Battery Applications: A Density Functional Theory Approach. Solids. 2022; 3(2):177-187. https://doi.org/10.3390/solids3020012
Chicago/Turabian StyleYanamandra, Kaushik, Rakesh K. Behera, Atef Daoud, and Nikhil Gupta. 2022. "Migration Barrier Estimation of Carbon in Lead for Lead–Acid Battery Applications: A Density Functional Theory Approach" Solids 3, no. 2: 177-187. https://doi.org/10.3390/solids3020012
APA StyleYanamandra, K., Behera, R. K., Daoud, A., & Gupta, N. (2022). Migration Barrier Estimation of Carbon in Lead for Lead–Acid Battery Applications: A Density Functional Theory Approach. Solids, 3(2), 177-187. https://doi.org/10.3390/solids3020012






