Experimental Investigations of Effective Thermal Conductivity of the Selected Examples of Steel Porous Charge
Abstract
1. Introduction
2. Materials and Methods
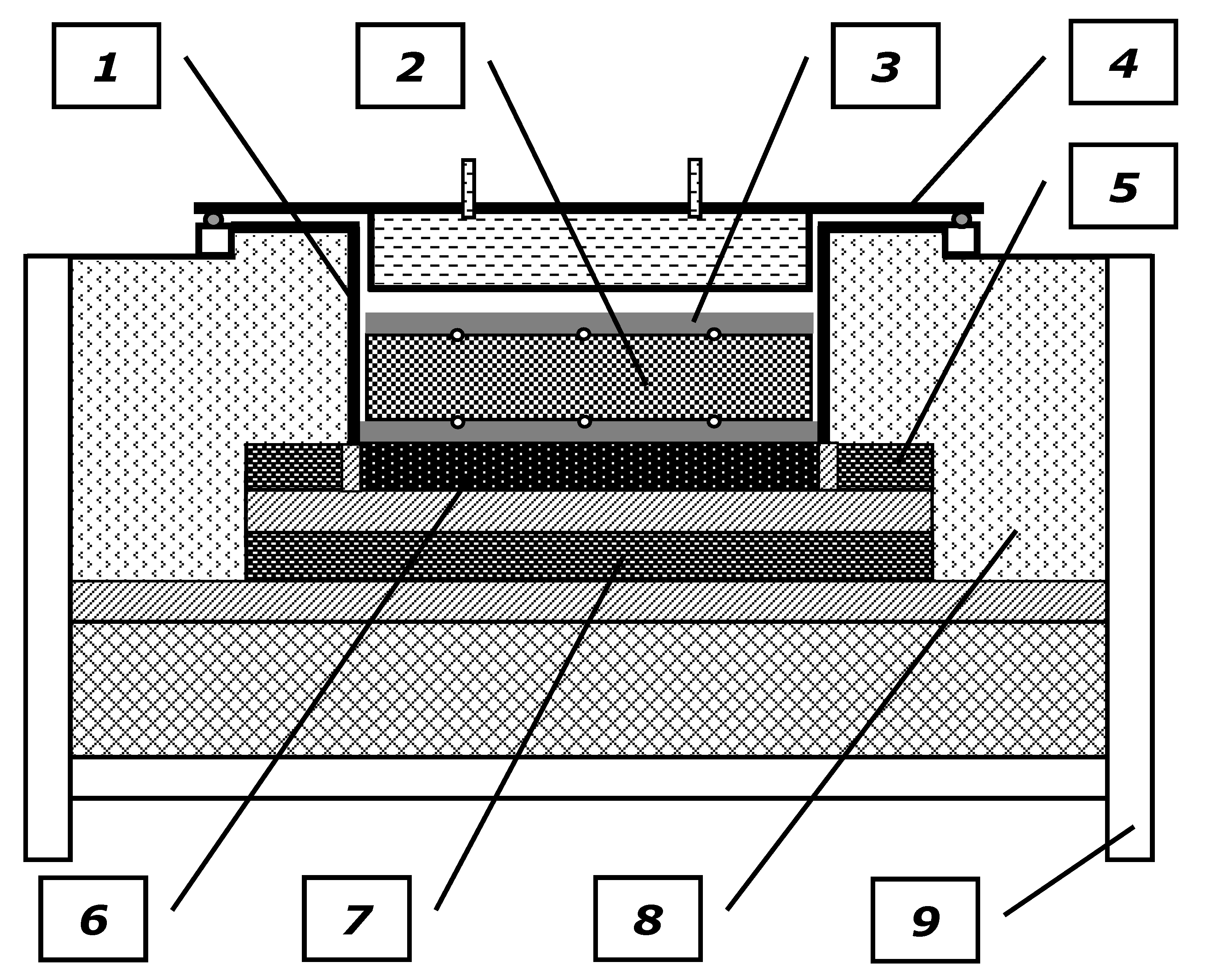
2.1. Experimental Setup
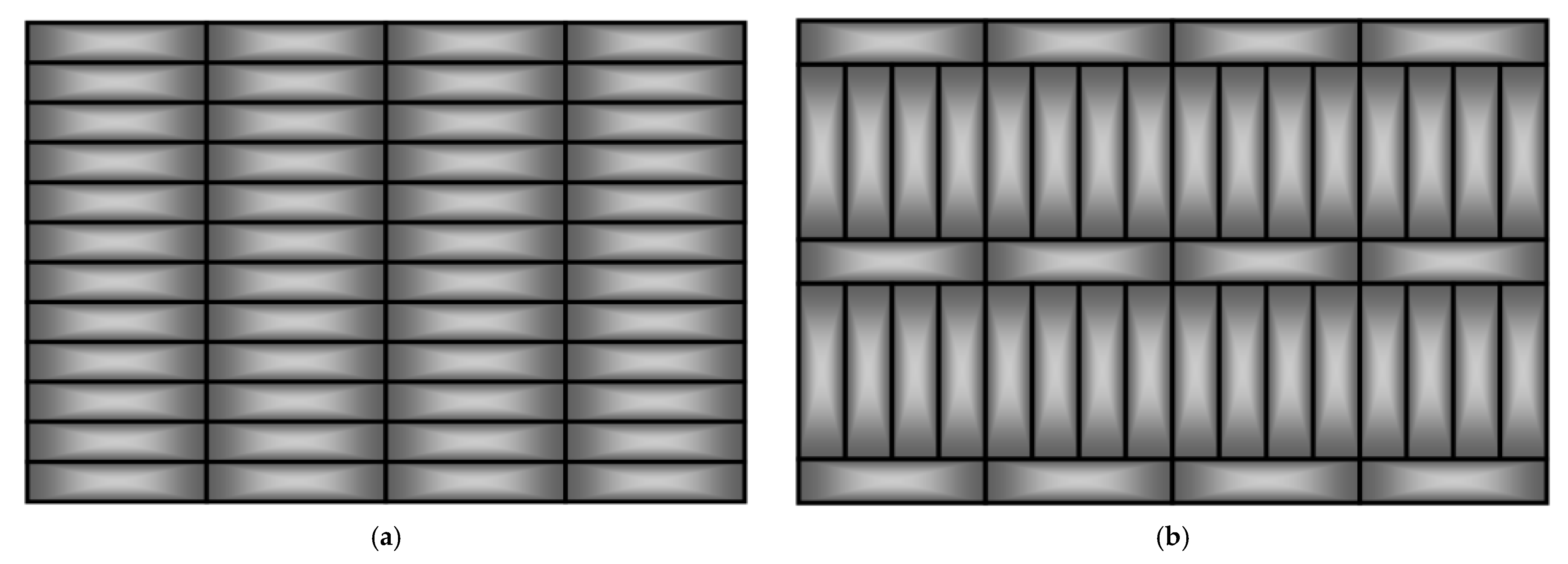
2.2. Investigated Samples
2.3. Measurement Procedure
2.4. Measurement Uncertainty
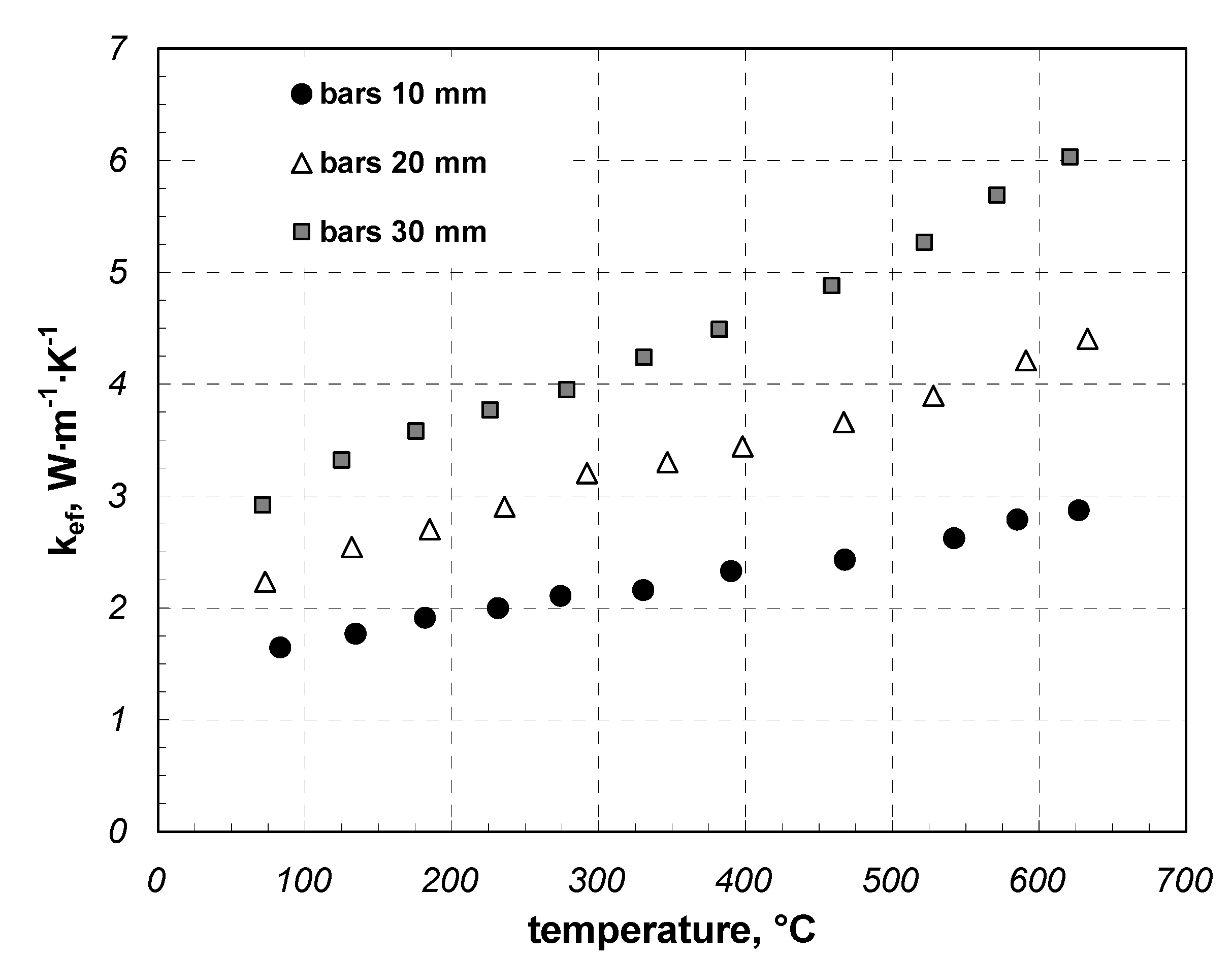
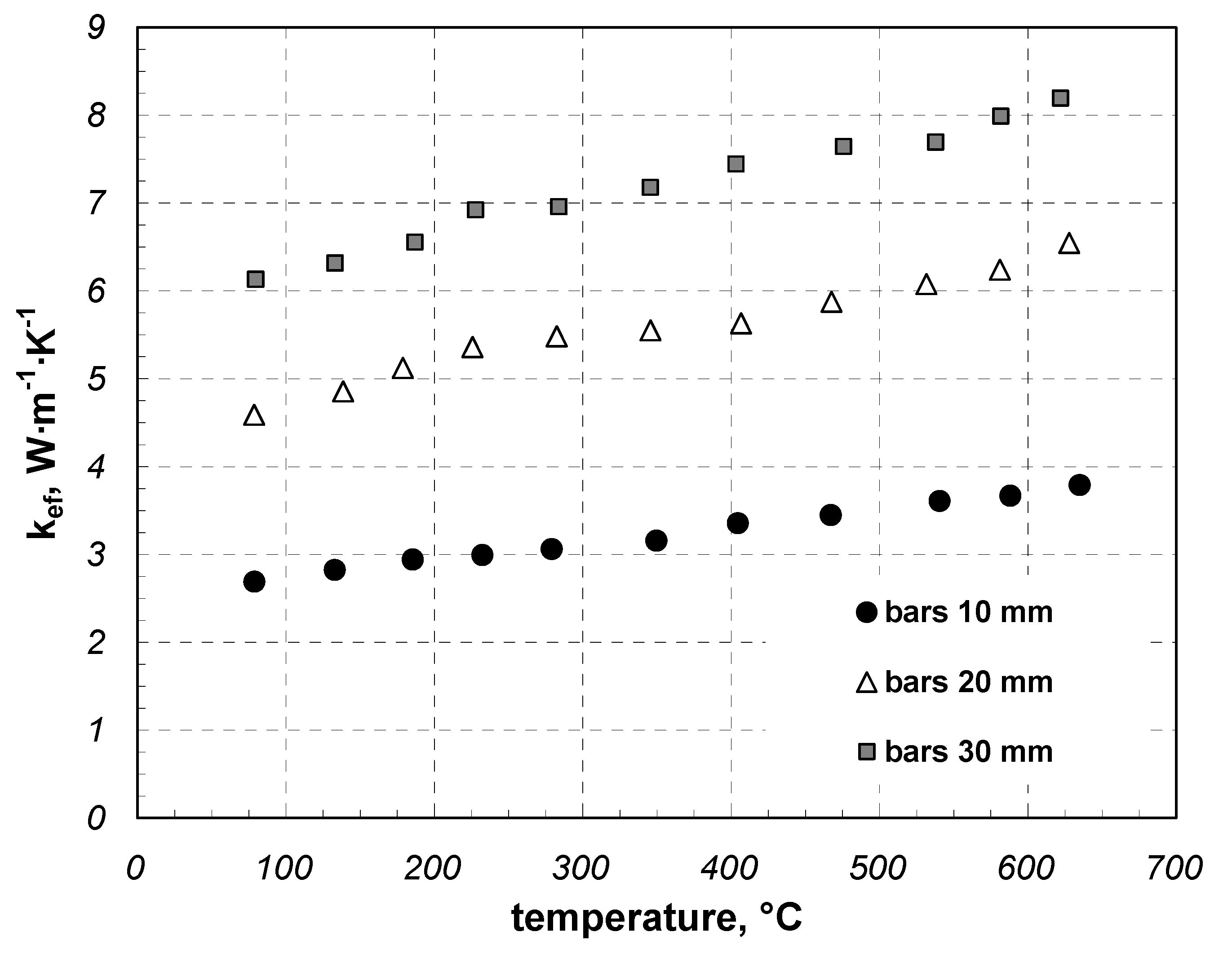
3. Results and Discussion
4. Conclusions
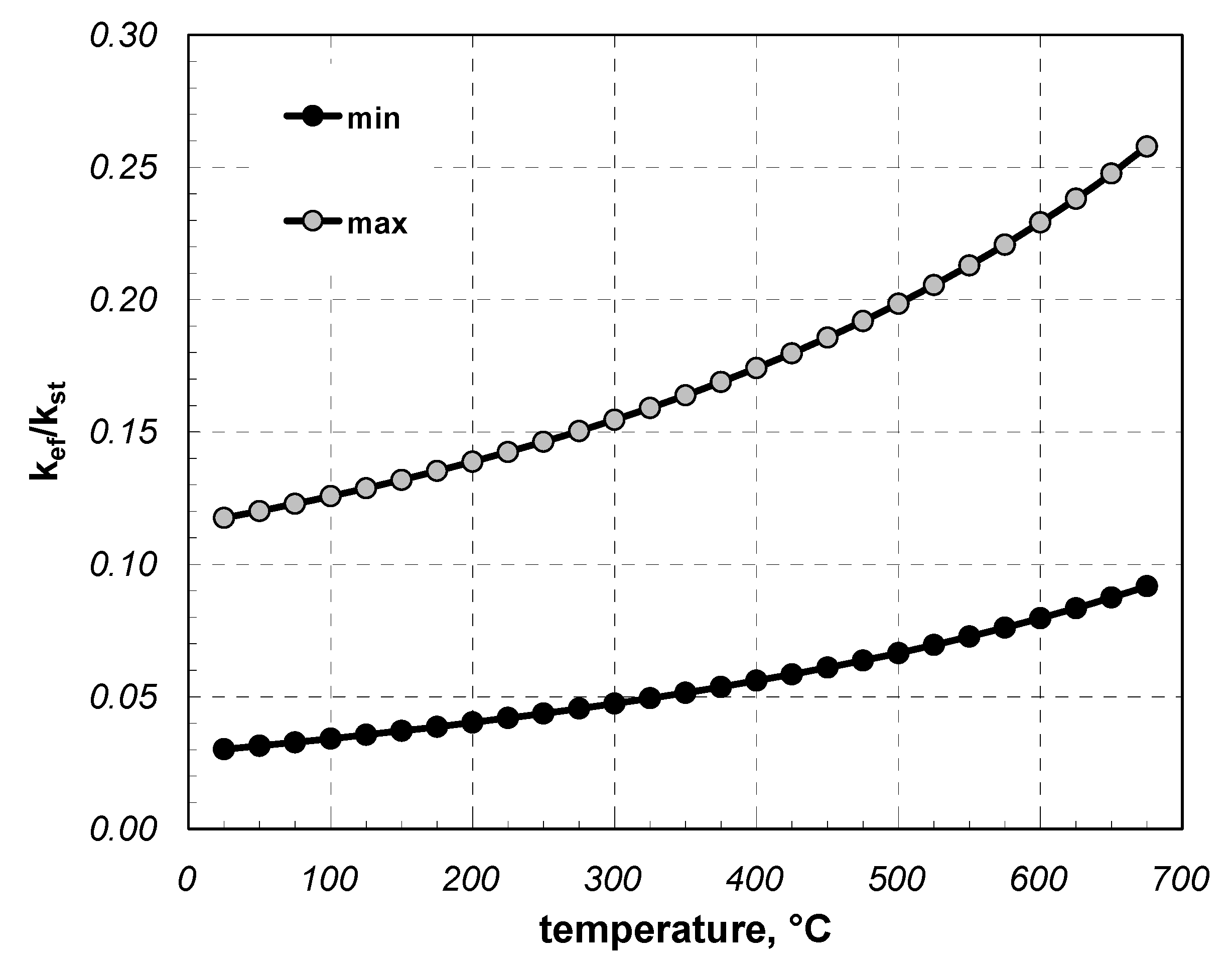
- Depending on the temperature, size, shape, and arrangement, the effective thermal conductivity of packed bundles of various long components made of low-carbon steel changes over the range of 1.7–8.2 W·m−1·K−1;
- The values of coefficient kef range from 0.03 to 0.25 of thermal conductivity of the solid phase of the charge;
- The effective thermal conductivity rises linearly with temperature, whereas the intensity of this increase and the value of coefficient kef depend on the transverse dimension of the components that form the charge;
- Coefficient kef declines with the increase in the external porosity of the charge, which depends on the transverse shape of the components and their arrangement;
- A lower effect on the value of kef is observed from internal porosity that concerns hollow components and is related to their geometry;
- A substantial impact on the value of coefficient kef is observed for thermal contact resistance, occurring between the adjacent components of the charge, with the value of this resistance depending mainly on the real contact area in the joints.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Totten, G.E. (Ed.) Steel Heat Treatment Handbook. Metallurgy and Technologies; CRC Taylor & Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Sahay, S.S.; Kapur, P.C. Model Based Scheduling of a Continuous Annealing Furnace. Iron Steelmak. 2007, 34, 262–268. [Google Scholar] [CrossRef]
- Jaluria, Y. Numerical Simulation of the Transport Process in a Heat Treatment Furnace. Int. J. Numer. Methods Eng. 1988, 25, 387–399. [Google Scholar] [CrossRef]
- Rao, T.R.; Barth, G.J.; Miller, J.R. Computer Model Prediction of Heating, Soaking and Cooking Times in Batch Coil Annealing. Iron Steel Eng. 1983, 60, 22–33. [Google Scholar]
- Sahay, S.S.; Krishnan, K. Model Based Optimization of Continuous Annealing Operation for Bundle of Packed Rods. Ironmak. Steelmak. 2007, 29, 89–94. [Google Scholar] [CrossRef]
- Ginkul, S.I.; Biryukov, A.B.; Ivanova, A.A.; Gnitiev, P.A. Predictive Mathematical Model of the Process of Metal Heating in Walking-Beam Furnaces. Metallurgist 2018, 62, 15–21. [Google Scholar] [CrossRef]
- Kim, M.Y. A Heat Transfer Model for the Analysis of Transient Heating of the Slab in a Direct-Fired Walking Beam Type Reheating Furnace. Int. J. Heat Mass Transf. 2007, 50, 3740–3748. [Google Scholar] [CrossRef]
- Shelton, S.N. Thermal Conductivity of Some Irons and Steels Over the Temperature Range 100 to 500 C. Stand. J. Res. 1934, 12, 441–449. [Google Scholar] [CrossRef]
- Cengel, Y.A. Heat and Mass Transfer. A Practical Approach, 3rd ed.; Mc Graw Hill: New York, NY, USA, 2002. [Google Scholar]
- Spur, G.; Stoferle, T. (Eds.) Handbuch der Fertigungstechnik; Carl Hausner: Munich, Germany, 1987; Volume 4/2. (In German) [Google Scholar]
- Wyczolkowski, R.; Musial, D. The Experimental Study of Natural Convection within the Space of a Bundle of Rectangular Sections. Exp. Therm. Fluid Sci. 2013, 51, 122–134. [Google Scholar] [CrossRef]
- Wyczólkowski, R.; Urbaniak, D. Modeling of Radiation in Bar Bundles Using the Thermal Resistance Concept. J. Thermophys. Heat Transf. 2016, 30, 721–729. [Google Scholar] [CrossRef]
- Musiał, M. Numerical Analysis of the Process of Heating of a Bed of Steel Bars. Arch. Metall. Mater. 2013, 1, 63–66. [Google Scholar] [CrossRef]
- Kolmasiak, C.; Wyleciał, T. Heat Treatment of Steel Products as an Example of Transport Phenomenon in Porous Media. Metalurgija 2018, 57, 363–366. [Google Scholar]
- Kaviany, M. Principles of Heat Transfer in Porous Media, 2nd ed.; Springer: New York, NY, USA, 1995. [Google Scholar]
- van Antverpen, W.; du Toit, C.G.; Rousseau, P.G. A Review of Correlations to Model the Packing Structure and Effective Thermal Conductivity in Packed Beds of Mono-Sized Spherical Particles. Nucl. Eng. Des. 2010, 240, 1803–1818. [Google Scholar] [CrossRef]
- Öchsner, A.; Murch, G.E.; de Lemos, M.J.S. (Eds.) Cellular and Porous Materials: Thermal Properties Simulation and Prediction; WILEY-VCH Verlag GmbH & Co, KGaA: Wenheim, Germany, 2008. [Google Scholar]
- Tavman, I.H. Effective Thermal Conductivity of Granular Porous Material. Int. Commun. Heat Mass Transf. 1996, 23, 169–176. [Google Scholar] [CrossRef]
- Cheng, P.; Hsu, T.C. The Effective Stagnant Thermal Conductivity of Porous Media with Periodic Structures. J. Porous Media 1999, 2, 19–38. [Google Scholar] [CrossRef]
- Palaniswamy, S.K.A.; Venugopal, P.R.; Palaniswamy, K. Effective Thermal Conductivity Modeling with Primary and Secondary Parameters for Two-Phase Materials. Therm. Sci. 2010, 14, 393–407. [Google Scholar] [CrossRef]
- Zuo, Y.; Wu, W.; Zhang, X.; Lin, L.; Xiang, S.; Liu, T.; Niu, L.; Huang, X. A Study of Heat Transfer in High-Performance Hydrogen Bell-Type Annealing Furnace. Heat Transf. Asian Res. 2001, 30, 615–623. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, F.; Wu, W.; Zuo, Y. Application of Radial Effective Thermal Conductivity for Heat Transfer Model of Steel Coils in HPH Furnace. Int. J. Thermophys. 2003, 24, 1395–1405. [Google Scholar] [CrossRef]
- Saboonchi, A.; Hassanpour, S.; Abbasi, S. New Heating Schedule in Hydrogen Annealing Furnace Based on Process Simulation for Less Energy Consumption. Energy Convers. Manag. 2008, 49, 3211–3216. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Lu, T.J.; Hodson, H.P.; Jackson, J.D. The Temperature Dependence of Effective Thermal Conductivity of Open-Celled Steel Alloy Foams. Mater. Sci. Eng. A 2004, 367, 123–131. [Google Scholar] [CrossRef]
- Peak, J.W.; Kang, B.H.; Kim, S.Y.; Hyun, J.M. Effective Thermal Conductivity and Permeability of Aluminum Foam Materials. Int. J. Thermophys. 2000, 21, 453–464. [Google Scholar] [CrossRef]
- Zhang, B.M.; Zhao, S.Y.; He, X.D. Experimental and Theoretical Studies on High-Temperature Thermal Properties of Fibrous Insulation. J. Quant. Spect. Radiat. Trans. 2008, 109, 1309–1324. [Google Scholar] [CrossRef]
- Edet, C.O.; Ushie, P.O.; Ekpo, C.M. Effect of additives on the thermal conductivity of loamy soil in cross river university of technology (crutech) farm, Calabar. Asian J. Phys. Chem. Sci. 2017, 3, 1–8. [Google Scholar] [CrossRef]
- Xu, Y.; Jiang, L.; Liu, J.; Zhang, Y.; Xu, J.; He, G. Experimental study and modeling on effective thermal conductivity of EPS lightweight concrete. J. Therm. Sci. Technol. 2015, 11, JTST0023. [Google Scholar] [CrossRef]
- Janjarasskul, T.; Lee, S.; Inoue, S.; Matsumura, Y.; Charinpanitkul, T. Enhancement of the effective thermal conductivity in packed beds by direct synthesis of carbon nanotubes. J. Therm. Sci. Technol. 2015, 10, JTST0013. [Google Scholar] [CrossRef]
- ASTM C1044-12. Standard Practice for Using a Guarded-Hot-Plate Apparatus or Thin-Heater Apparatus in the Single-Sided Mode; ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar]
- ASTM C177-13. Standard Test Method for Steady-State Heat Flux Measurements and Thermal Transmission Properties by Means of the Guarded-Hot-Plate Apparatus; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- Temperature Sensor TP-201_206 (Sheathed Thermocouple). Available online: https://www.czaki.pl/en/produkt/temperature-sensor-tp-201_206/ (accessed on 17 November 2021).
- EMT-200 Temperature Meter. Available online: https://www.czaki.pl/en/produkt/emt-200-temperature-meter/ (accessed on 17 November 2021).
- Saving Energy with Electric Resistance Heating. Available online: https://www.nrel.gov/docs/legosti/fy97/6987.pdf (accessed on 17 November 2021).
- 3-Phase Power Network Meter N14. Available online: https://www.lumel.com.pl/en/catalogue/product/3-phase-power-network-meter-n14 (accessed on 17 November 2021).
- European Steel and Alloy Grades/Numbers Steel Number. Available online: http://www.steelnumber.com/en/steel_composition_eu.php?name_id=645 (accessed on 30 July 2021).
- Taylor, J.R. An Introduction to Error Analysis; The Study of Uncertainties in Physical Measurements, 2nd ed.; University Science Book: Sausaliti, CA, USA, 1997. [Google Scholar]
- Breitbah, G.; Barthels, H. The Radiant Heat Transfer in the High Temperature Reactor Core After Failure of the Heat Removal System. Nucl. Technol. 1980, 49, 392–399. [Google Scholar] [CrossRef]
- Wyczółkowski, R.; Gała, M.; Szwaja, S.; Piotrowski, A. Determination of the Radiation Exchange Factor in the Bundle of Steel Round Bars. Energies 2021, 14, 5263. [Google Scholar] [CrossRef]
- Wyczółkowski, R. Computational model of complex heat flow in the area of steel rectangular section. Proc. Eng. 2016, 157, 185–192. [Google Scholar] [CrossRef][Green Version]
- Wyczółkowski, R.; Szmidla, J.; Gała, M.; Bagdasaryan, V. Analysis of Nusselt Number for Natural Convection in Package of Square Steel Sections. Acta Phys. Pol. A 2020, 139, 548–551. [Google Scholar] [CrossRef]
- Wyczółkowski, R.; Gała, M.; Bagdasaryan, V. Model of Complex Heat Transfer in the Package of Rectangular Steel Sections. Appl. Sci. 2020, 10, 9044. [Google Scholar] [CrossRef]
- Mikic, B.B. Thermal Contact Conductance: Theoretical Consideration. Int. J. Heat Transf. 1974, 17, 205–214. [Google Scholar] [CrossRef]
- Shridar, M.R.; Yovanovich, M.M. Review of Elastic and Plastic Contact Conductance Models: Comparison with Experiment. J. Thermophys. Heat Transf. 1994, 8, 633–640. [Google Scholar] [CrossRef]
- Kolmasiak, C.; Bagdasaryan, V.; Wyleciał, T.; Gała, M. Analysing the Contact Conduction Influence on the Heat Transfer Intensity in the Rectangular Steel Bars Bundle. Materials 2021, 14, 5655. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Zhang, H.; Yang, Z.; Zhang, J. The Effective Thermal Conductivity of Three-Dimensional Reticulated Foam Material. J. Porous Mater. 2009, 16, 65–71. [Google Scholar] [CrossRef]
- Wyczółkowski, R.; Strychalska, D.; Bagdasaryan, V. Correlations for the Thermal Conductivity of Selected Steel Grades as a Function of Temperature in the Range of 0–800 °C. Unpublished Work Accepted for Publication at Scientific Conference “XV Research & Development in Power Engineering Conference, Warshaw. 2021. Available online: https://www.rdpe.itc.pw.edu.pl/public/site/2021/A_BOOK_OF_ABSTRACTS_RDPE_2021_11_30.pdf (accessed on 15 December 2021).
- Wyczółkowski, R.; Bagdasaryan, V.; Szwaja, S. On Determination of the Effective Thermal Conductivity of a Bundle of Steel Bars Using the Krischer Model and Considering Thermal Radiation. Materials 2021, 14, 4378. [Google Scholar] [CrossRef]
- Carson, J.K. A Versatile Effective Thermal Diffusivity Model for Porous Materials. Int. J. Thermophys. 2021, 42, 141. [Google Scholar] [CrossRef]





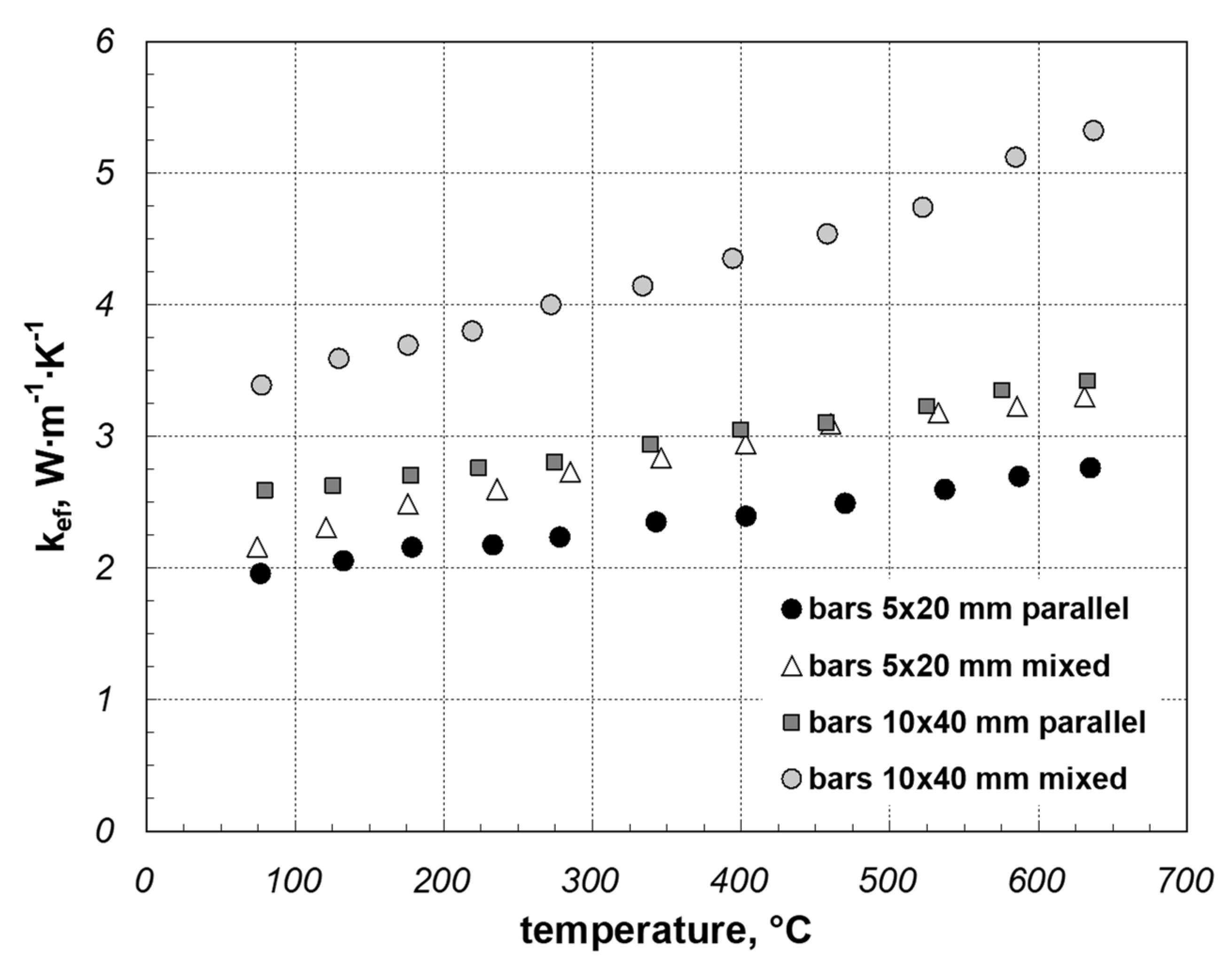

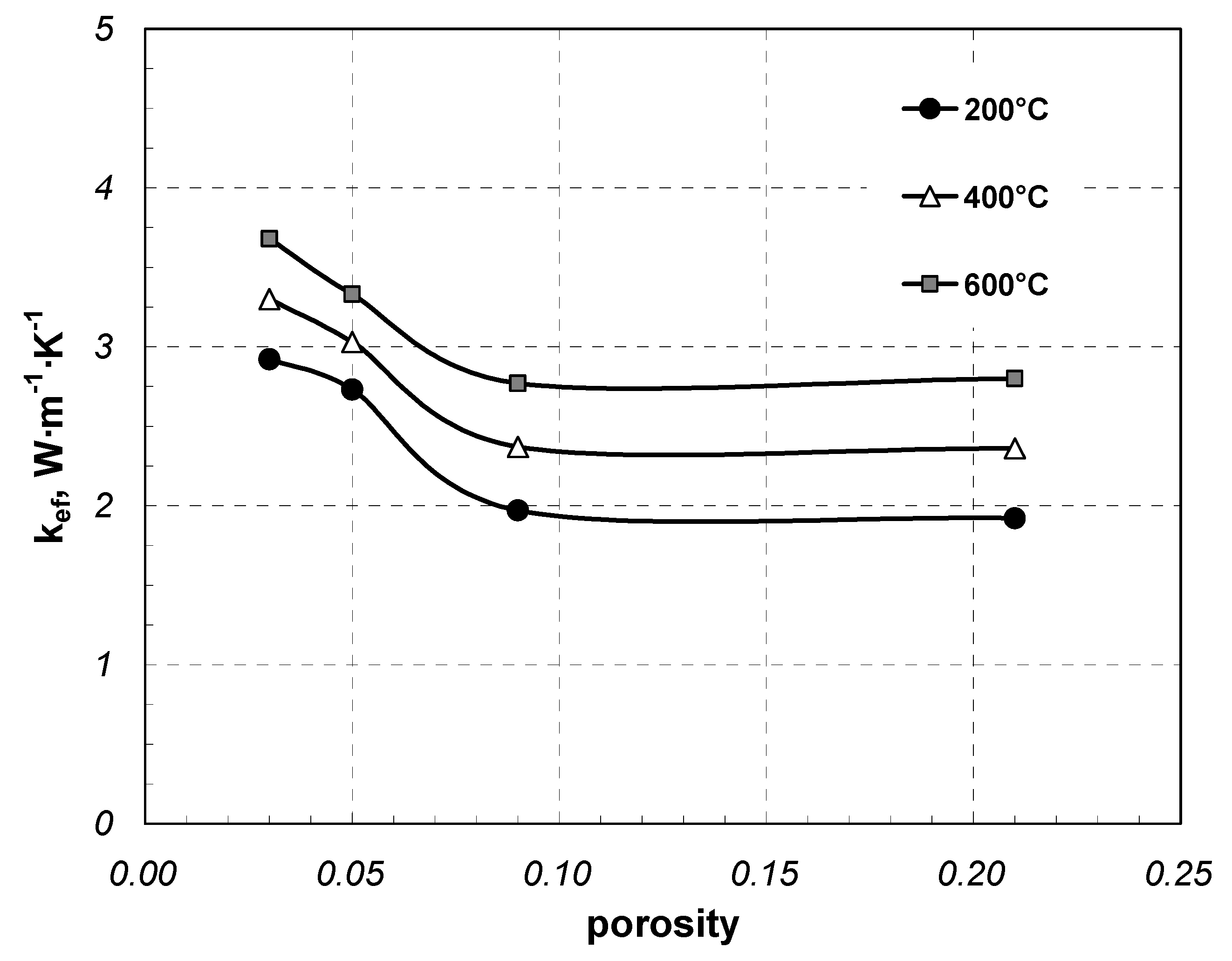
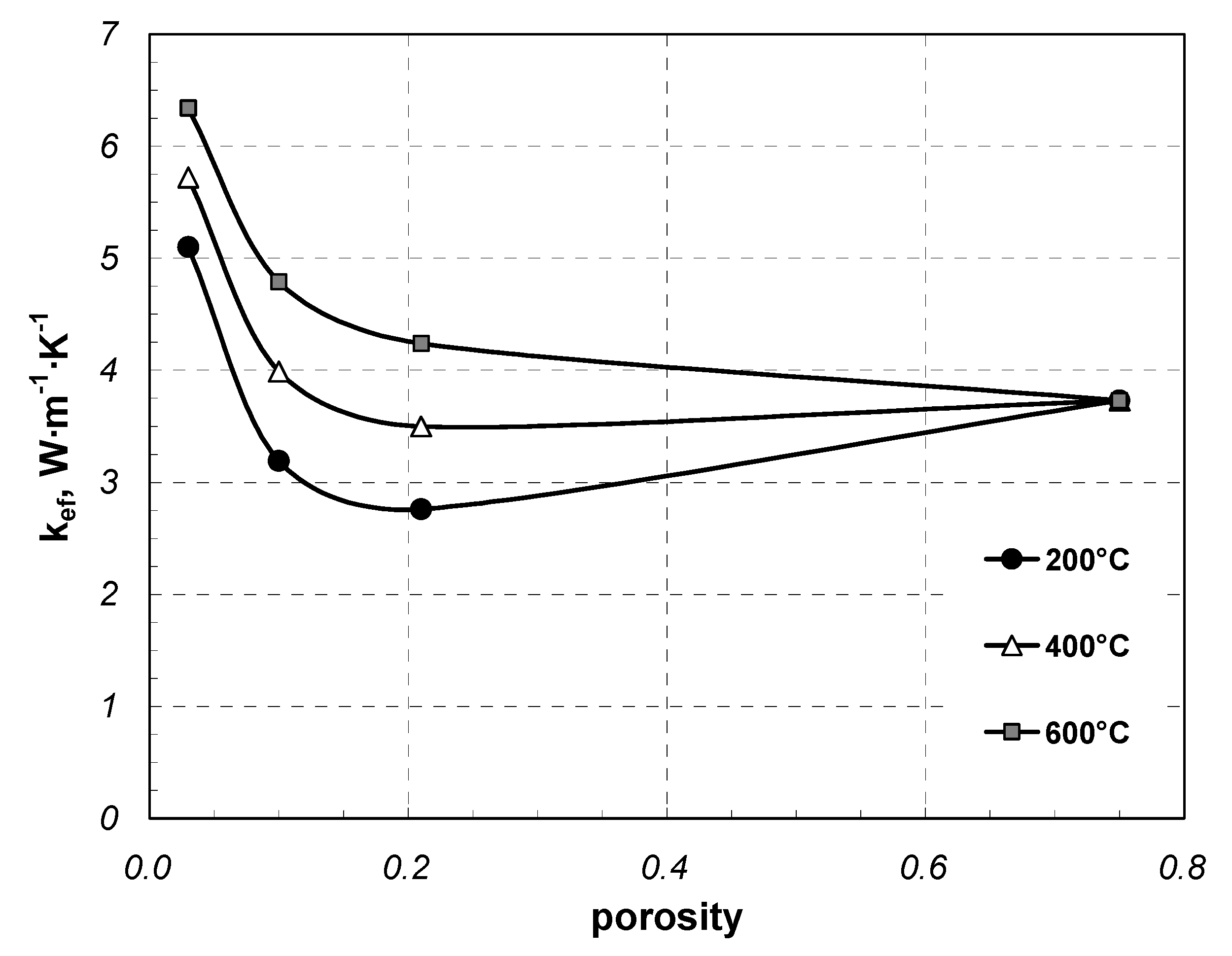
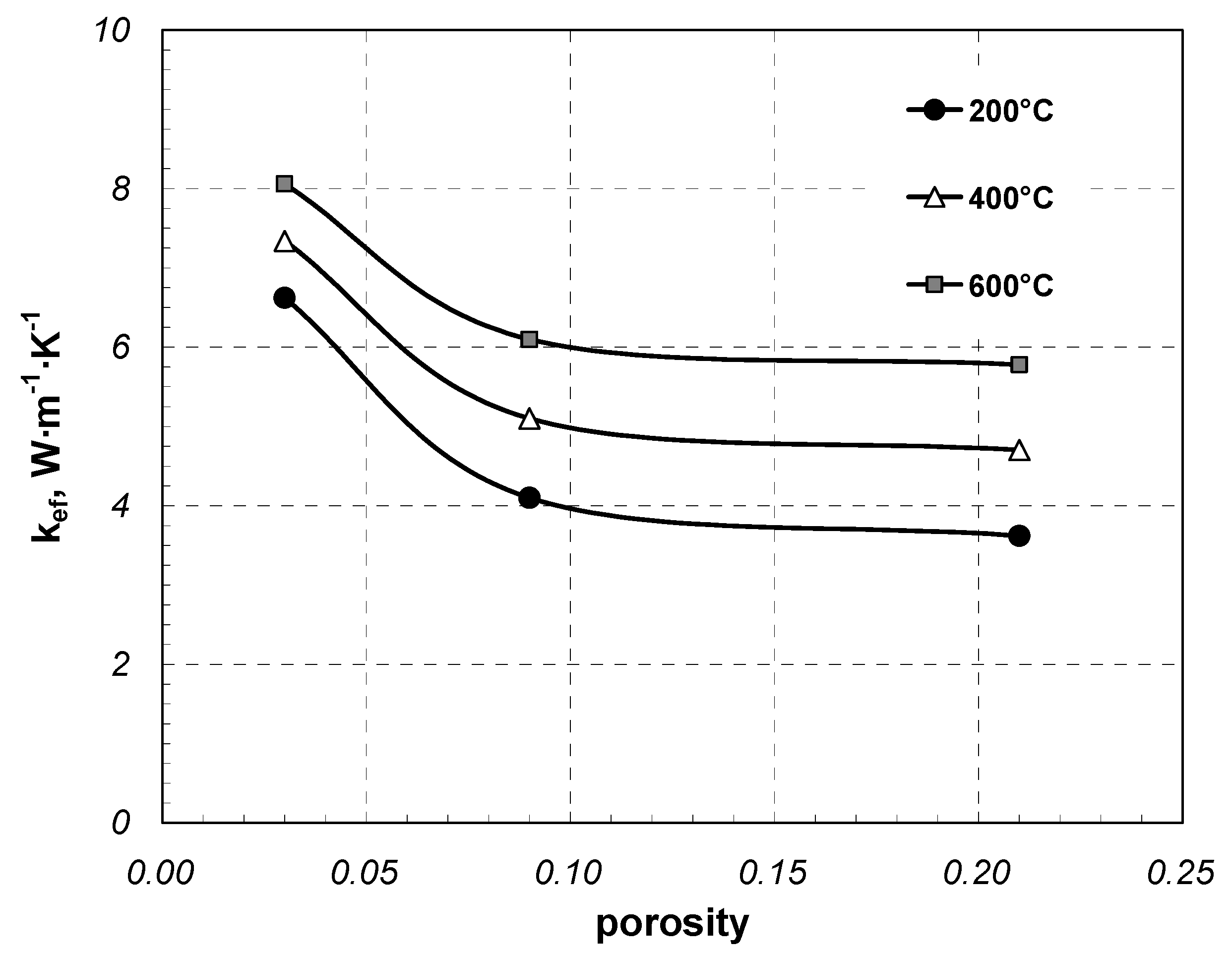
| Sample Type | Element Dimension | k0 | β | R2 |
|---|---|---|---|---|
| Staggered round bars | 10 mm | 1.57 | 0.0021 | 0.981 |
| 20 mm | 2.39 | 0.0042 | 0.974 | |
| 30 mm | 3.11 | 0.0051 | 0.998 | |
| In-line round bars | 10 mm | 1.48 | 0.0022 | 0.993 |
| 20 mm | 2.02 | 0.0037 | 0.993 | |
| 30 mm | 2.54 | 0.0054 | 0.990 | |
| Square bars | 10 mm | 2.54 | 0.0019 | 0.994 |
| 20 mm | 4.48 | 0.0031 | 0.967 | |
| 30 mm | 5.91 | 0.0036 | 0.982 | |
| Parallel flat bars | 5 × 20 mm | 1.86 | 0.0014 | 0.993 |
| 10 × 40 mm | 2.43 | 0.0015 | 0.992 | |
| Mixed flat bars | 5 × 20 mm | 2.10 | 0.0021 | 0.980 |
| 10 × 40 mm | 3.09 | 0.0033 | 0.988 | |
| Sections | 40 × 40 mm | 3.95 | 0.0019 | 0.984 |
| 60 × 60 mm | 4.18 | 0.0031 | 0.977 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wyczółkowski, R. Experimental Investigations of Effective Thermal Conductivity of the Selected Examples of Steel Porous Charge. Solids 2021, 2, 420-436. https://doi.org/10.3390/solids2040027
Wyczółkowski R. Experimental Investigations of Effective Thermal Conductivity of the Selected Examples of Steel Porous Charge. Solids. 2021; 2(4):420-436. https://doi.org/10.3390/solids2040027
Chicago/Turabian StyleWyczółkowski, Rafał. 2021. "Experimental Investigations of Effective Thermal Conductivity of the Selected Examples of Steel Porous Charge" Solids 2, no. 4: 420-436. https://doi.org/10.3390/solids2040027
APA StyleWyczółkowski, R. (2021). Experimental Investigations of Effective Thermal Conductivity of the Selected Examples of Steel Porous Charge. Solids, 2(4), 420-436. https://doi.org/10.3390/solids2040027






