An Induced Seismicity Indicator Using Accumulated Microearthquakes’ Frictional Energy
Abstract
1. Introduction
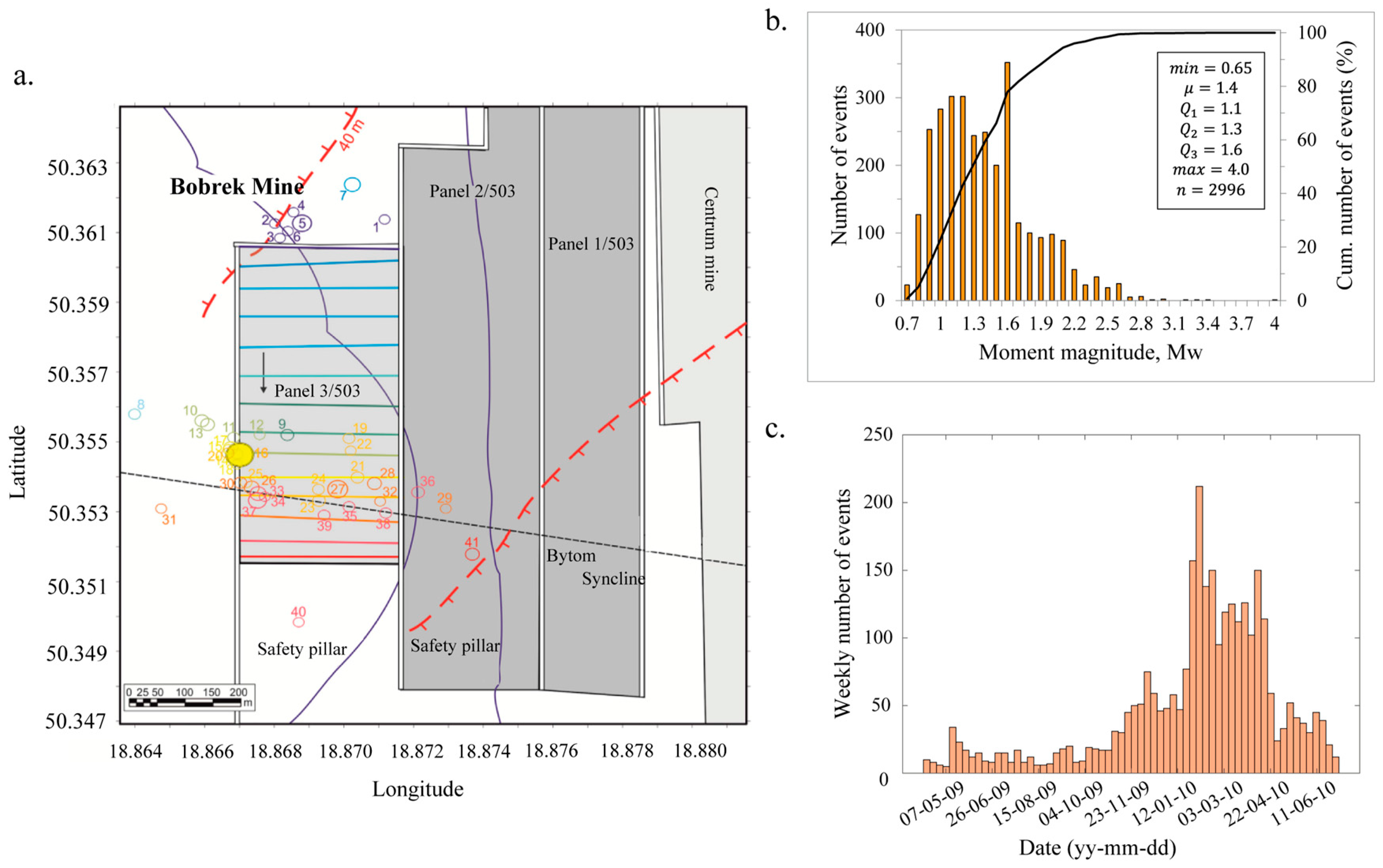
2. Geological Setting
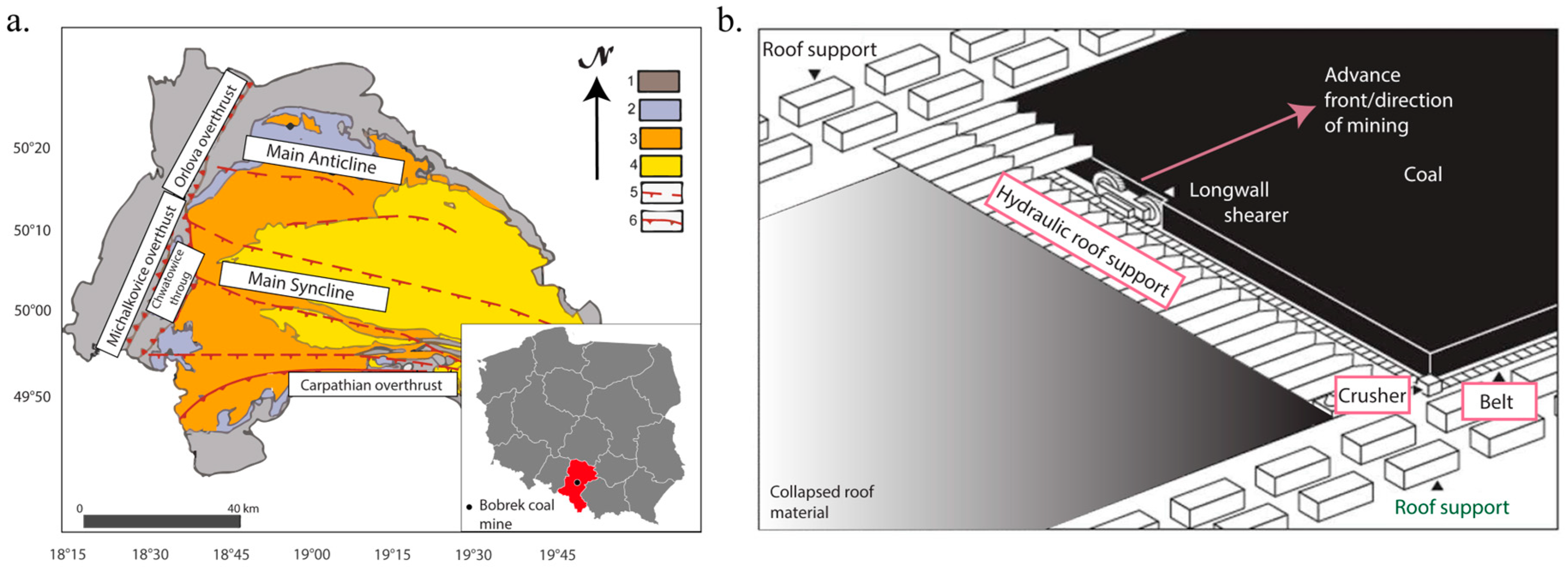
3. Data
4. Methodology
4.1. Earthquake’s Frictional Energy
4.2. Accumulated Frictional Heat (AFH)
- Q > Q*: An alert state is defined. If during the next Δtf hours a seismic event with magnitude M ≥ Mw* occurs, this is classified as a True Positive (TP).
- Q > Q*: An alert state is defined. If during the next Δtf hours a seismic event with magnitude M ≥ Mw* does not occur, this is classified as a False Positive (FP).
- Q < Q*: No alert state is defined. If during the next Δtf hours a seismic event with magnitude M ≥ Mw* occurs, this is classified as a False Negative (FN).
- Q < Q*: No alert state is defined. If during the next Δtf hours a seismic event with magnitude M ≥ Mw* does not occur, this is classified as a True Negative (TN).
4.3. Performance Analysis
4.4. PSS Maximization Procedure
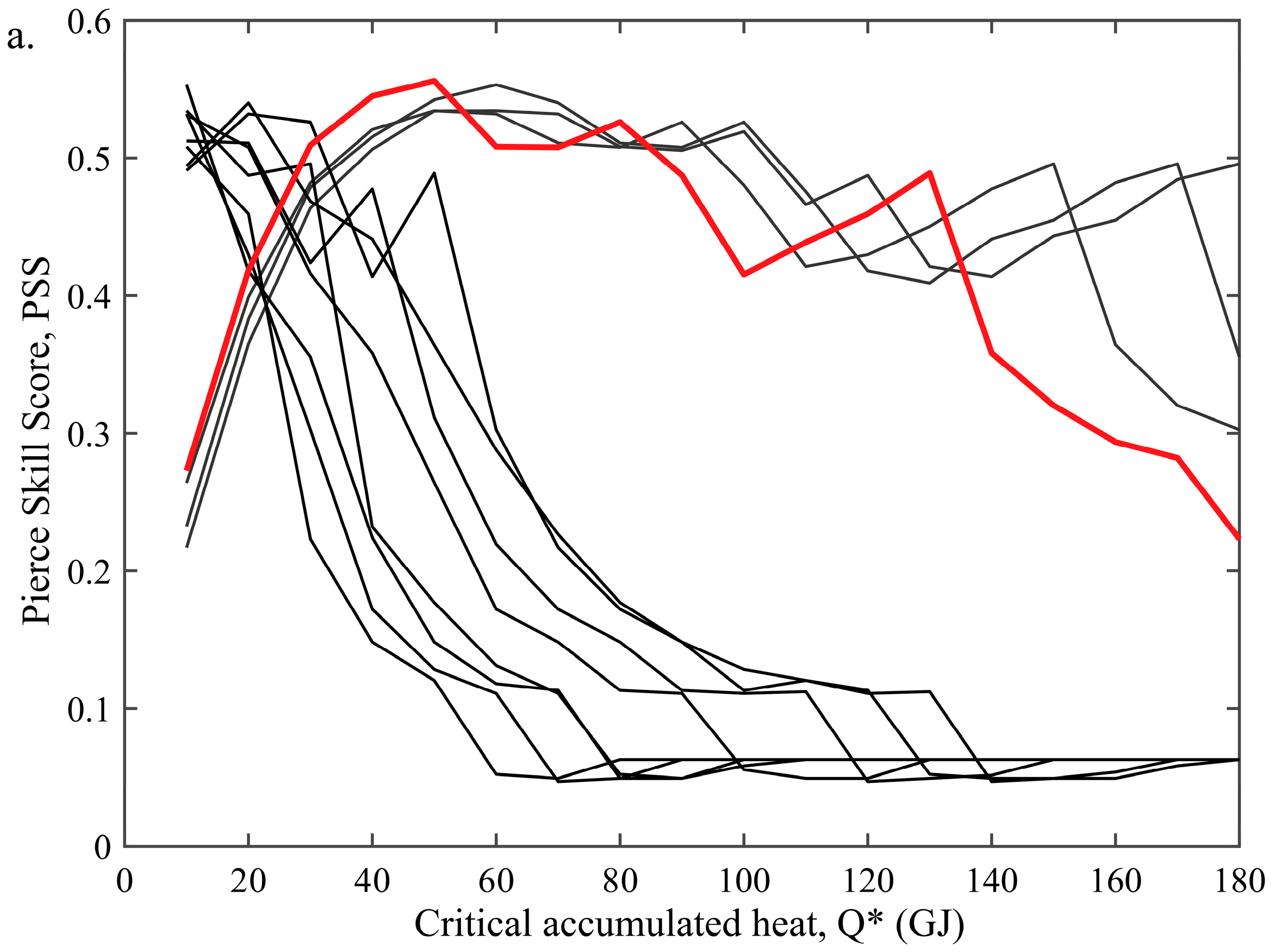
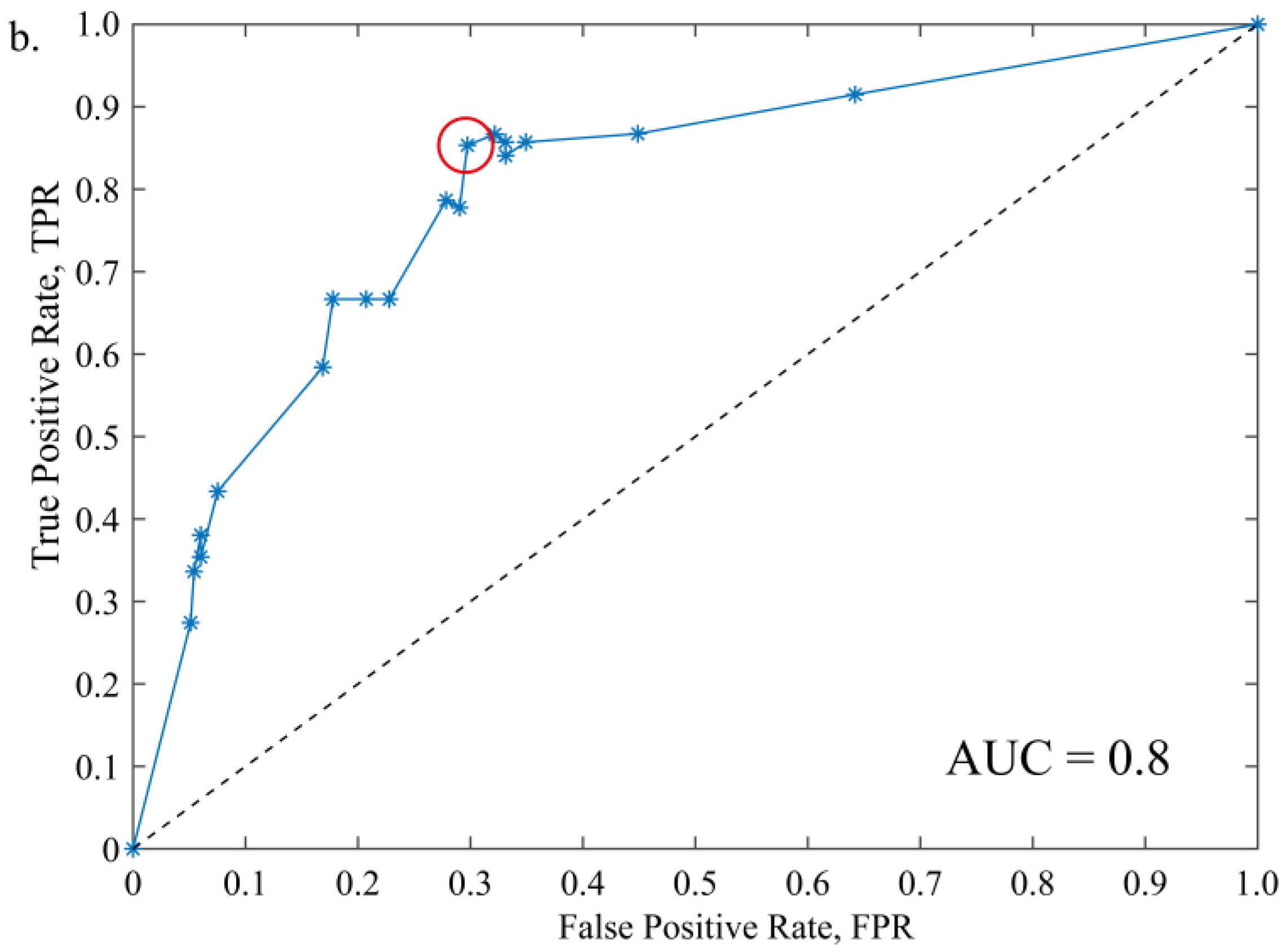
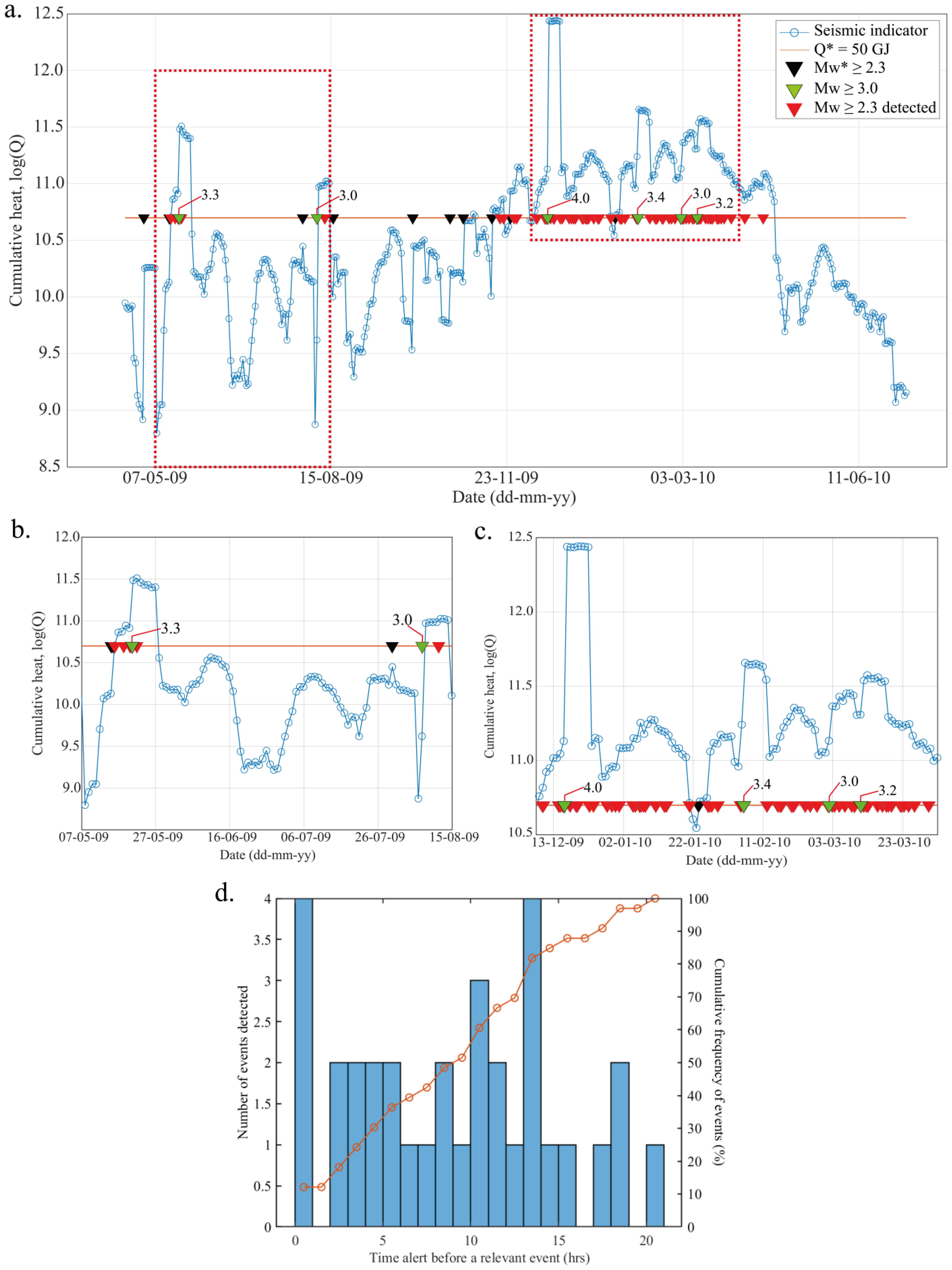
5. Results
6. Discussions and Conclusions
- (i)
- Attempt to empirically define the AFH method decay rate in order to be able to propose a re-entry protocol.
- (ii)
- Consider the relative spatial distance between events, as heat accumulation and transfer strongly depend on how the earthquakes are distributed.
- (iii)
- Seismicity monitoring and forecasting are topics of large concern in different contexts, such as geothermal and CO2 injection [51,52]. In general, the most-used monitoring technique is Probabilistic Seismic Hazard Analysis (PSHA) [53]. To our knowledge, the application of probabilistic approaches such as the one presented in this study and others [21,22] is not an extended practice. Due to this, we plan to apply the AFH method to new datasets considering fracturing behavior induced by fluid injection.
- (iv)
- In consideration of the abovementioned seismic network functioning, a real-time monitoring test is planned for the AFH methodology.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kaiser, P.K.; McCreath, D.R.; Tannant, D.D.; Brummer, R.K.; Vasek, M.; Yi, X.P. Rockburst support-volume 2 of rockburst research handbook. In Canadian Rockburst Research Program 1990–1995; CAMIRO Mining Division: Sudbury, ON, Canada, 1996. [Google Scholar]
- Li, C.C.; Mikula, P.; Simser, B.; Hebblewhite, B.; Joughin, W.; Feng, X.; Xu, N. Discussions on rockburst and dynamic ground support in deep mines. J. Rock Mech. Geotech. Eng. 2019, 11, 1110–1118. [Google Scholar] [CrossRef]
- Salamon, M.D.G. Rockburst hazard and the fight for its alleviation in South African gold mines. In Rockbursts-Prediction and Control; Institute of Mines and Metallurgy: London, UK, 1983; pp. 11–36. [Google Scholar]
- Gibowicz, S.; Kijko, A. An Introduction to Mine Seismology; Academic press: San Diego, CA, USA, 1994. [Google Scholar]
- Potvin, Y.; Hadjigeorgiou, J.; Stacey, T.R.; Potvin, Y. Challenges in Deep and High Stress Mining; Australian Centre for Geomechanics: Perth, Australia, 2007. [Google Scholar]
- Sernageomin. Balance Nacional de Accidentabilidad Minera de 2016. Available online: https://www.sernageomin.cl/accidentabilidad-minera/ (accessed on 26 February 2023). (In Spanish).
- Sernageomin. Accidentabilidad Minera año 2019. Available online: https://www.sernageomin.cl/accidentabilidad-minera/ (accessed on 26 February 2023).
- Stein, S.; Wyssession, M. Introduction to Seismology, Earthquakes and Earth Structure; Blackwell science Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Kanamori, H. Energy Budget of Earthquakes and Seismic Efficiency. In Earthquake Thermodynamics and Phase Transformations in the Earth’s Interior; International Geophysics Series 76; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Kanamori, H.; Heaton, T. Microscopic and macroscopic physics of earthquakes. In Geocomplexity and the Physics of Earthquakes; Rundle, J.B., Turcotte, D.L., Klein, W., Eds.; Geophysical Mono-Graph Series 120; AGU: Washington, DC, USA, 2000. [Google Scholar]
- Di Toro, G.; Han, R.; Hirose, T.; De Paola, N.; Nielsen, S.; Mizoguchi, K.; Ferri, F.; Cocco, M.; Shimamoto, T. Fault lubrication during earthquakes. Nature 2011, 471, 494–498. [Google Scholar] [CrossRef]
- Aubry, J.; Passelègue, F.X.; Deldicque, D.; Girault, F.; Marty, S.; Lahfid, A.; Bhat, H.S.; Escartin, J.; Schubnel, A. Frictional heating processes and energy budget during laboratory earthquakes. Geophys. Res. Lett. 2018, 45, 12274–12282. [Google Scholar] [CrossRef]
- Byerlee, J. Friction of rocks. Pure Appl. Geophys. 1978, 116, 615–626. [Google Scholar] [CrossRef]
- Kanamori, H.; Rivera, L. Energy Partitioning During an Earthquake. In Earthquakes: Radiated Energy and the Physics of Faulting; Abercrombie, R., McGarr, A., Di Toro, G., Kanamori, H., Eds.; Geophysical Monograph Series 170; American Geophysical Union: Washington, DC, USA, 2006. [Google Scholar]
- Pavez, C.; Estay, R.; Brönner, M.; Ortiz, A.; Debarbieri, F.; Ibañez, J.P.; Guzmán, L. Frictional energy patterns related to the temperature increases due to intraplate seismicity, southern Norway, 2000–2019 catalogue. Nor. J. Geol. 2021, 101, 202105. [Google Scholar] [CrossRef]
- Ogata, Y. Statistical models for earthquake occurrences and residual analysis for point. J. Am. Stat. Assoc. 1988, 83, 9–27. [Google Scholar] [CrossRef]
- Vallejos, J.; Estay, R.; Zepeda, R.; Jorquiera, P. A methodology for evaluating the performance of seismic indicators at El Teniente Mine, Chile. In Proceedings of the 6th International Conference & Exhibition on Mass Mining, Massmin, Sudbury, ON, Canada, 10–14 June 2012. [Google Scholar]
- Estay, R. Metodología para la Evaluación del Desempeño de Indicadores Sísmicos en Sismicidad Inducida por la Minería. Master’s Thesis, Universidad de Chile, Santiago, Chile, 2014. (In Spanish). [Google Scholar]
- Vergara, M. Evaluación del Desempeño del Indicador de Agloramiento Espacial Con Datos de Sismicidad Inducida por Minería. Bachelor’s Thesis, Universidad Técnica Federico Santa María, Santiago, Chile, 2021. (In Spanish). [Google Scholar]
- Vallejos, J.A. Analysis of Seismicity in Mines and Development of Re-Entry Protocols. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2010. [Google Scholar]
- Hudyma, M.; Heal, D.; Mikula, P. Seismic monitoring in mines–Old technology, new applications. In Seismic Monitoring in Mines-Old Technology, New Applications; Hebblewhite, B.K., Ed.; University of New South Wales School of Mining Engineering: Sydney, NSW, Australia, 2003. [Google Scholar]
- Mendecki, A.; van Aswegen, G.; Mountfort, P. A guide to routine seismic monitoring in mines. In A Handbook on Rock Engineering Practices for Tabular Hard Rock Mines; Jager, A.J., Ryder, J.A., Eds.; Creda Communications: Cape Town, South Africa, 1999. [Google Scholar]
- Gutenberg, B.; Richter, C.F. Seismicity of the Earth. Geol. Soc. Am. Bull. 1945, 56, 603–667. [Google Scholar] [CrossRef]
- Holub, K. Spasce-time variations of the frequency-energy relation for mining induced seismicity in the Ostrava-Karviná mining district. Pure Appl. Geophys. 1996, 146, 265–280. [Google Scholar] [CrossRef]
- Ma, X.; Westman, E.; Slaker, B.; Thibodeau, D.; Counter, D. The b-value evolution of mining-induced seismicity and mainshock occurrences at hard-rock mines. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2018, 104, 64–70. [Google Scholar] [CrossRef]
- Mukuhira, Y.; Fehler, M.C.; Bjarkason, E.K.; Ito, T.; Asanuma, H. On the b-value dependency of injection-induced seismicity on geomechanical parameters. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2024, 174, 105631. [Google Scholar] [CrossRef]
- Hudyma, M. Applied mine seismology concepts and techniques. In Technical Notes for ENGR 5356–Mine Seismic Monitoring Systems 2010; Laurentian University: Sudbury, ON, Canada, 2010. [Google Scholar] [CrossRef]
- Mendecki, A. Seismic ground motion alerts for mines. J. Seism. 2023, 27, 599–608. [Google Scholar] [CrossRef]
- Stec, K. Characteristics of seismic activity of the Upper Silesian Coal Basin in Poland. Geophys. J. Int. 2007, 168, 757–768. [Google Scholar] [CrossRef]
- Kędzior, S. Methane contents and coal-rank variability in the Upper Silesian Coal Basin, Poland. Int. J. Coal Geol. 2015, 139, 152–164. [Google Scholar] [CrossRef]
- IS EPOS Episode: Bobrek. Available online: https://tcs.ah-epos.eu/#episode:BOBREK (accessed on 26 February 2023).
- Saki, S.A. Gob Ventilation Borehole Design and Performance Optimization for Longwall Coal Mining Using Computational Fluid Dynamics. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 2016. [Google Scholar]
- Leptokaropoulos, K.; Staszek, M.; Cielesta, S.; Urban, P.; Olszewska, D.; Lizurek, G. Time-dependent seismic hazard in Bobrek coal mine, Poland, assuming different magnitude distribution estimations. Acta Geophys. 2017, 65, 493–505. [Google Scholar] [CrossRef]
- Kozlowska, M.; Orlecka-Sikora, B. Assessment of Quantitative Aftershock Productivity Potential in Mining-Induced Seismicity. Pure Appl. Geophys. 2016, 174, 925–936. [Google Scholar] [CrossRef]
- Mendecki, M.J.; Szczygiel, J.; Lizurek, G.; Teper, L. Mining-triggered seismicity governed by a fold hinge zone: The Upper Silesian Coal Basin, Poland. Eng. Geol. 2020, 274, 105728. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion and related problems. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Grünthal, G.; Wahlström, R.; Stromeyer, D. The unified catalogue of earthquakes in central, northern, and northwestern Europe (CENEC)-updated and expanded to the last millennium. J. Seism. 2009, 13, 517–541. [Google Scholar] [CrossRef]
- Madariaga, R. Implications of stress drop models of earthquakes from the inversion of stress drop from seismic observations. Pure Appl. Geophys. 1977, 115, 301–316. [Google Scholar] [CrossRef]
- Kanamori, H.; Anderson, D. Theoretical basis of some empirical relations in seismology. Bull. Seismo. Soc. Am. 1975, 65, 1073–1095. [Google Scholar] [CrossRef]
- Mendecki, M.J.; Wojtecki, Ł.; Zuberek, W.M. Case Studies of Seismic Energy Release Ahead of Underground Coal Mining Before Strong Tremors. Pure Appl. Geophys. 2019, 176, 3487–3508. [Google Scholar] [CrossRef]
- Abercrombie, R.; Leary, P. Source parameters of small earthquakes recorded at 2.5 km depth, Cajon Pass, southern California: Implications for earthquake scaling. Geophys. Res. Lett. 1993, 20, 1511–1514. [Google Scholar] [CrossRef]
- Xiong, J.; Lin, H.; Ding, H.; Pei, H.; Rong, C.; Liao, W. Investigation on thermal property parameters characteristics of rocks and its influence factors. Nat. Gas Ind. B 2020, 7, 298–308. [Google Scholar]
- Schön, J. (Ed.) Chapter 4—Density. In Developments in Petroleum Science; Elsevier: Amsterdam, The Netherlands, 2015; Volume 65, pp. 109–118. [Google Scholar]
- Weijermars, R. Principles of Rock Mechanics; Alboran Science Publications: Amsterdam, The Netherlands, 1997; p. 359. [Google Scholar]
- Jarosinski, M. Recent tectonic stress field investigations in Poland: A state of the art. Geol. Q. 2006, 50, 303–321. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Toksanbayev, N.; Adoko, A.C. Predicting rockburst damage scale in seismically active mines using a classifier ensemble approach. IOP Conferr. Ser. Earth Environ. Sci. 2023, 1124, 012102. [Google Scholar] [CrossRef]
- Peirce, C.S. The numerical measure of the success of predictions. Science 1884, 4, 453–454. [Google Scholar] [CrossRef]
- Mendecki, A. Real time quantitative seismology in mines. In Rockburst and Seismicity in Mines, Proceedings of the 3rd International Symposium, Kingston, ON, Canada, 16–18 August 1993; Young, R.P., Ed.; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Havskov, J.; Ottemöller, L.; Trnkoczy, A.; Bormann, P. Seismic Networks. In New Manual of Seismological Observatory Practice 2 (NMSOP-2); Bormann, P., Ed.; Deutsches GeoForschungsZentrum (GFZ): Potsdam, Germany, 2012. [Google Scholar]
- Zhou, W.; Lanza, F.; Grigoratos, I.; Schultz, R.; Cousse, J.; Trutnevyte, E.; Muntendam-Bos, A.; Wiemer, S. Managing induced seismicity risks from enhanced geothermal systems: A good practice guideline. Rev. Geophys. 2024, 62, e2024RG000849. [Google Scholar] [CrossRef]
- Cheng, Y.; Liu, W.; Xu, T.; Zhang, Y.; Zhang, X.; Xing, Y.; Feng, B.; Xia, Y. Seismicity induced by geological CO2 storage: A review. Earth-Sci. Rev. 2023, 239, 104369. [Google Scholar] [CrossRef]
- Baker, J.W. Introduction to Probabilistic Seismic Hazard Analysis. In White Paper Version 2.1; Cambridge University Press: Cambridge, UK, 2015; p. 77. [Google Scholar]

| Parameter | Range of Values for Sandstones |
|---|---|
| C (J/kg K) | 787–915 [42] |
| ρ (kg/m3) | 2000–2760 [43] |
| μ (GPA) | 4–30 [44] |
| ΔσS (MPA) | 0.1–10 [41] |
| σF (MPA) | 14.9–20 (considering an initial tectonic stress between 15 and 30 MPa [45]) |
| w (m) | 0.001–0.01 [10] |
| Parameter | Steps | Quantity |
|---|---|---|
| C (J/kg K) | 50 | 3 |
| ρ (Kg/m3) | 200 | 4 |
| μ (GPa) | 10 | 3 |
| ΔσS (MPa) | 4 | 4 |
| σF (MPa) | 2 | 4 |
| w (m) | 0.002 | 5 |
| Q* (GJ) | 10 | 18 |
| Mw* | 0.1 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estay, R.; Pavez-Orrego, C. An Induced Seismicity Indicator Using Accumulated Microearthquakes’ Frictional Energy. Mining 2025, 5, 27. https://doi.org/10.3390/mining5020027
Estay R, Pavez-Orrego C. An Induced Seismicity Indicator Using Accumulated Microearthquakes’ Frictional Energy. Mining. 2025; 5(2):27. https://doi.org/10.3390/mining5020027
Chicago/Turabian StyleEstay, Rodrigo, and Claudia Pavez-Orrego. 2025. "An Induced Seismicity Indicator Using Accumulated Microearthquakes’ Frictional Energy" Mining 5, no. 2: 27. https://doi.org/10.3390/mining5020027
APA StyleEstay, R., & Pavez-Orrego, C. (2025). An Induced Seismicity Indicator Using Accumulated Microearthquakes’ Frictional Energy. Mining, 5(2), 27. https://doi.org/10.3390/mining5020027







