The Effect of Initiation Time Delay and Sequencing on Rock Damage in Multi-Hole Blasting
Abstract
1. Introduction
2. Numerical Modelling Verification and Validation
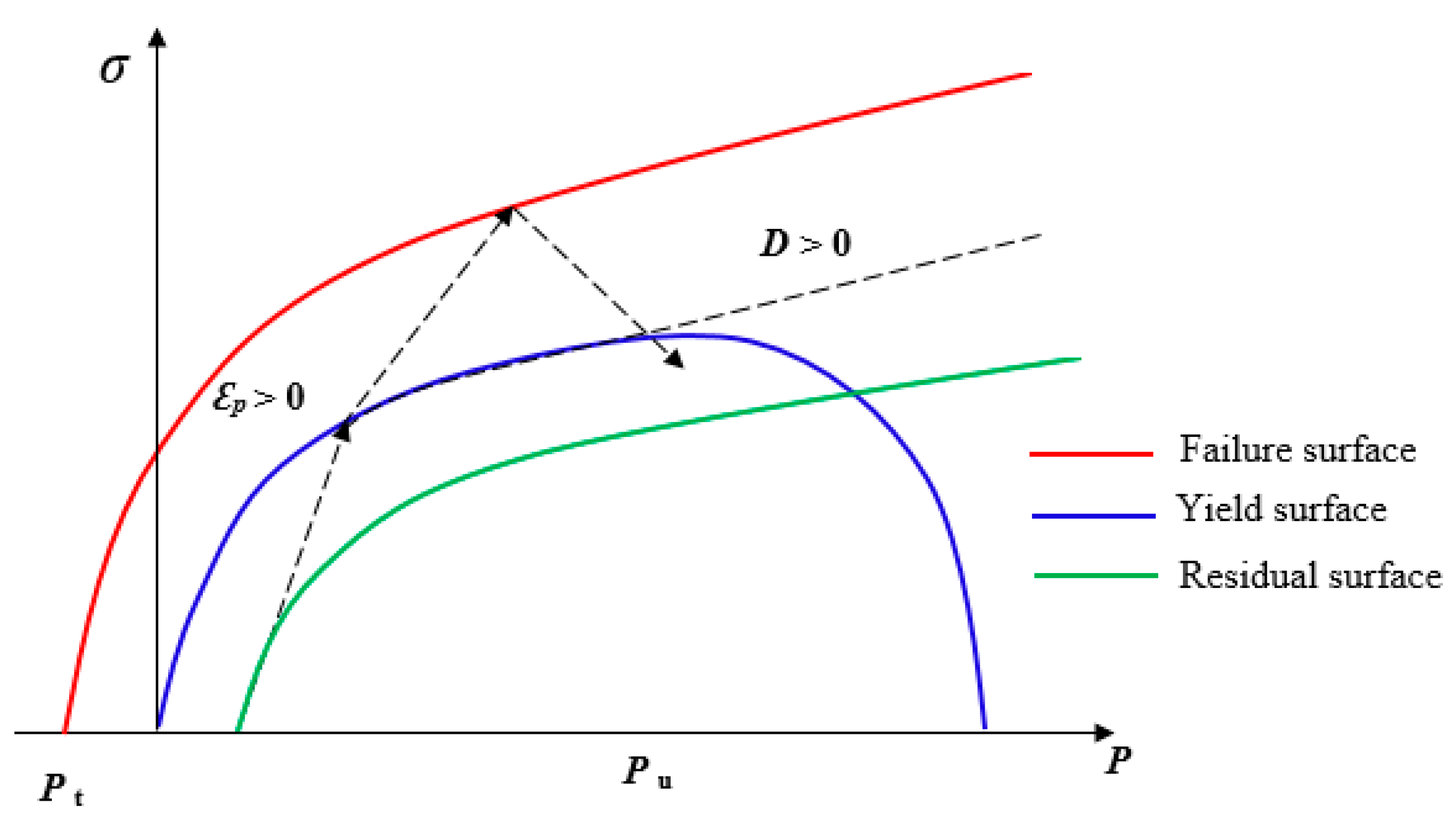
2.1. The RHT Material Model
2.2. Explosive Properties and Parameters
2.3. Simulation Model Preparation, Verification, and Validation
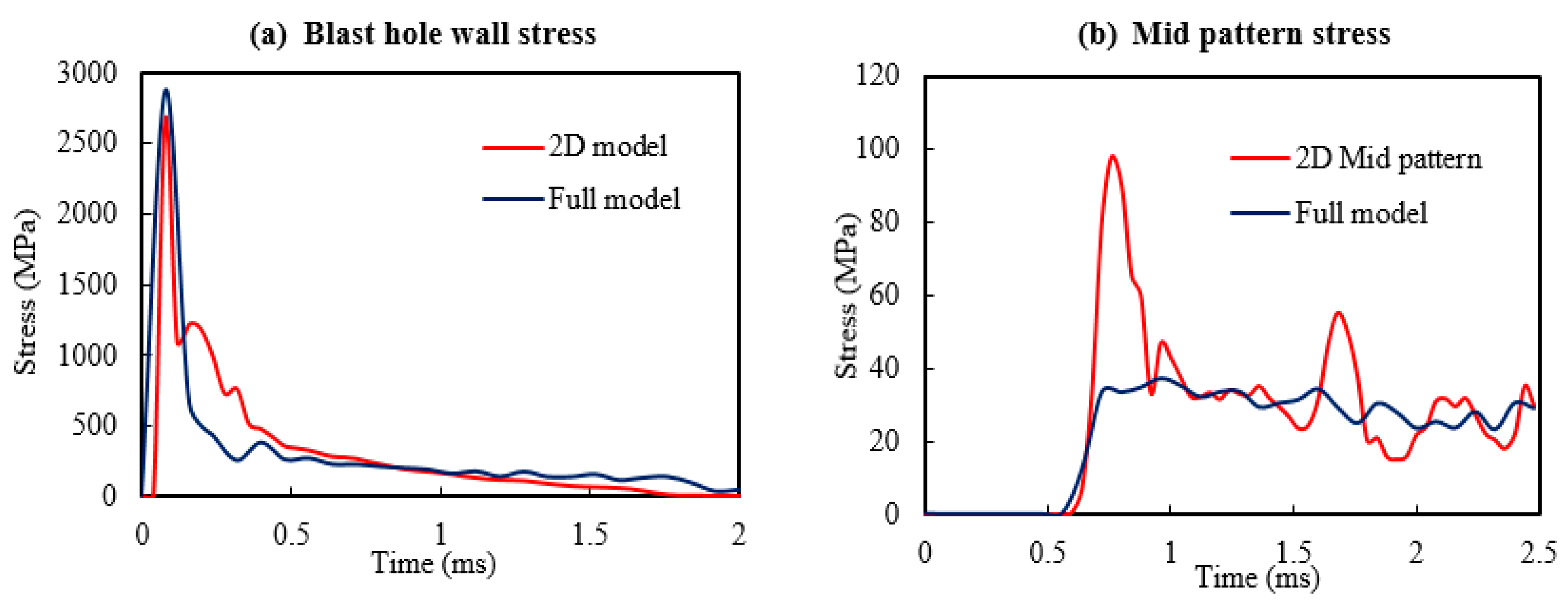
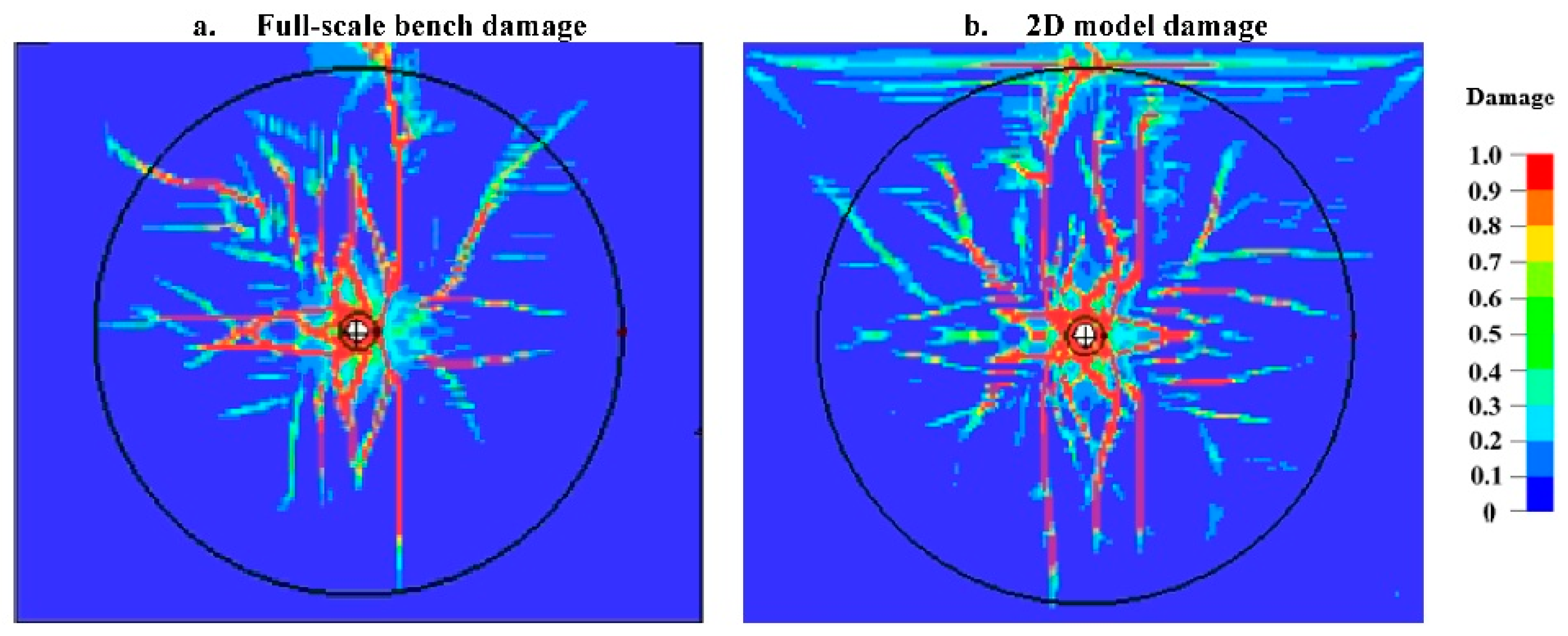
2.4. Full-Scale and 2D Model Comparison
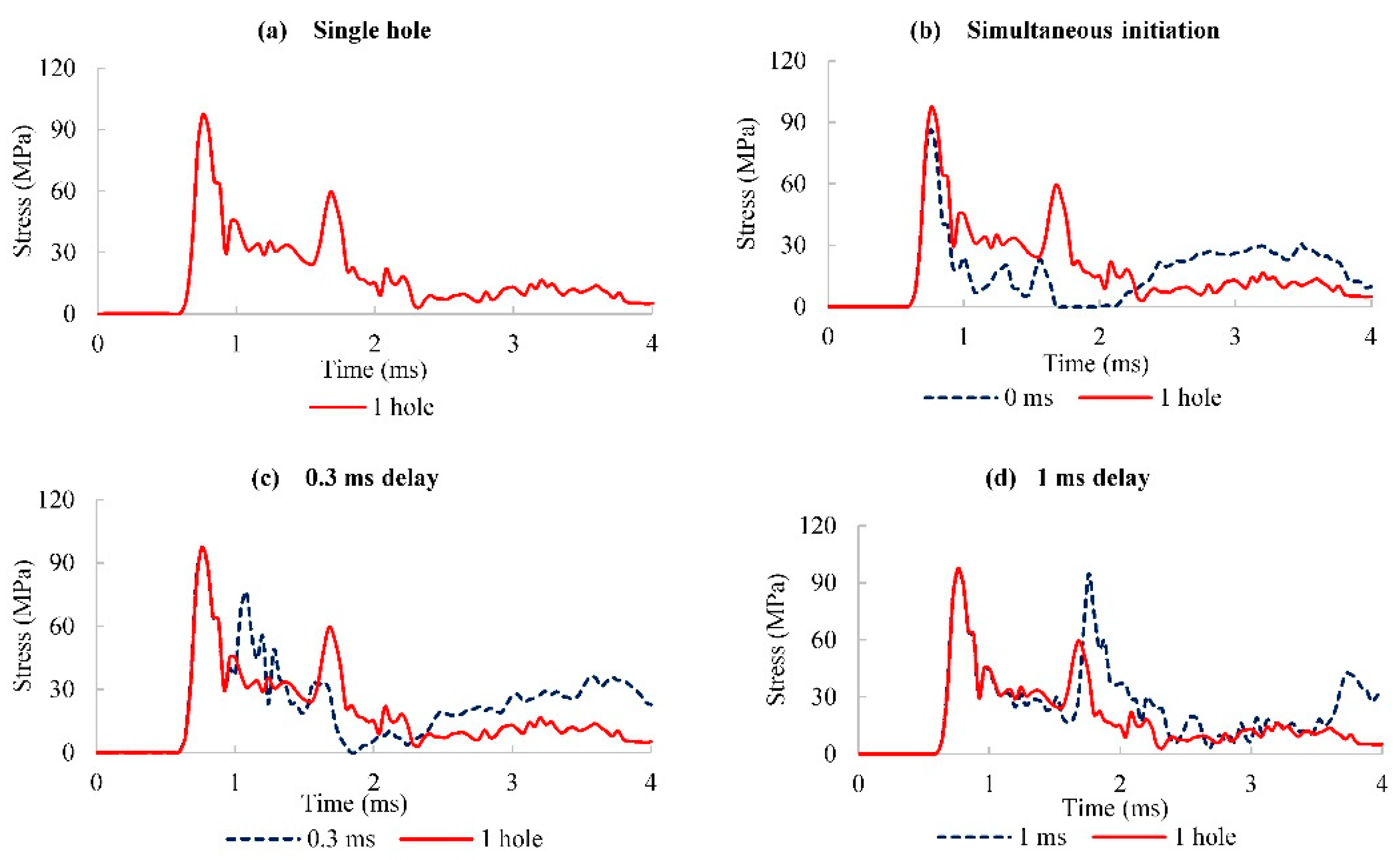
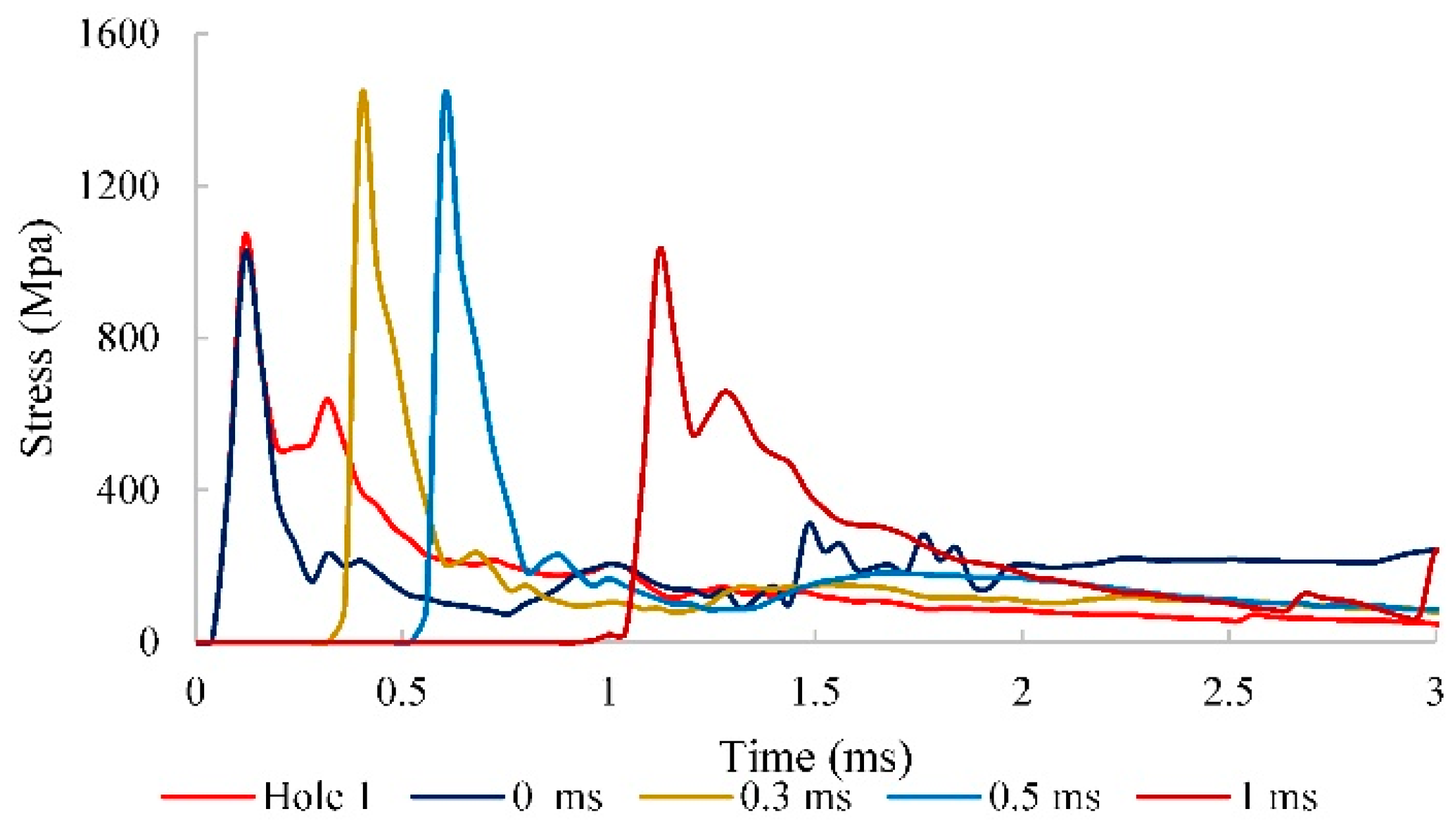
3. Multi-Hole Blasting and Interactions Between Blastholes
3.1. Intact Rock
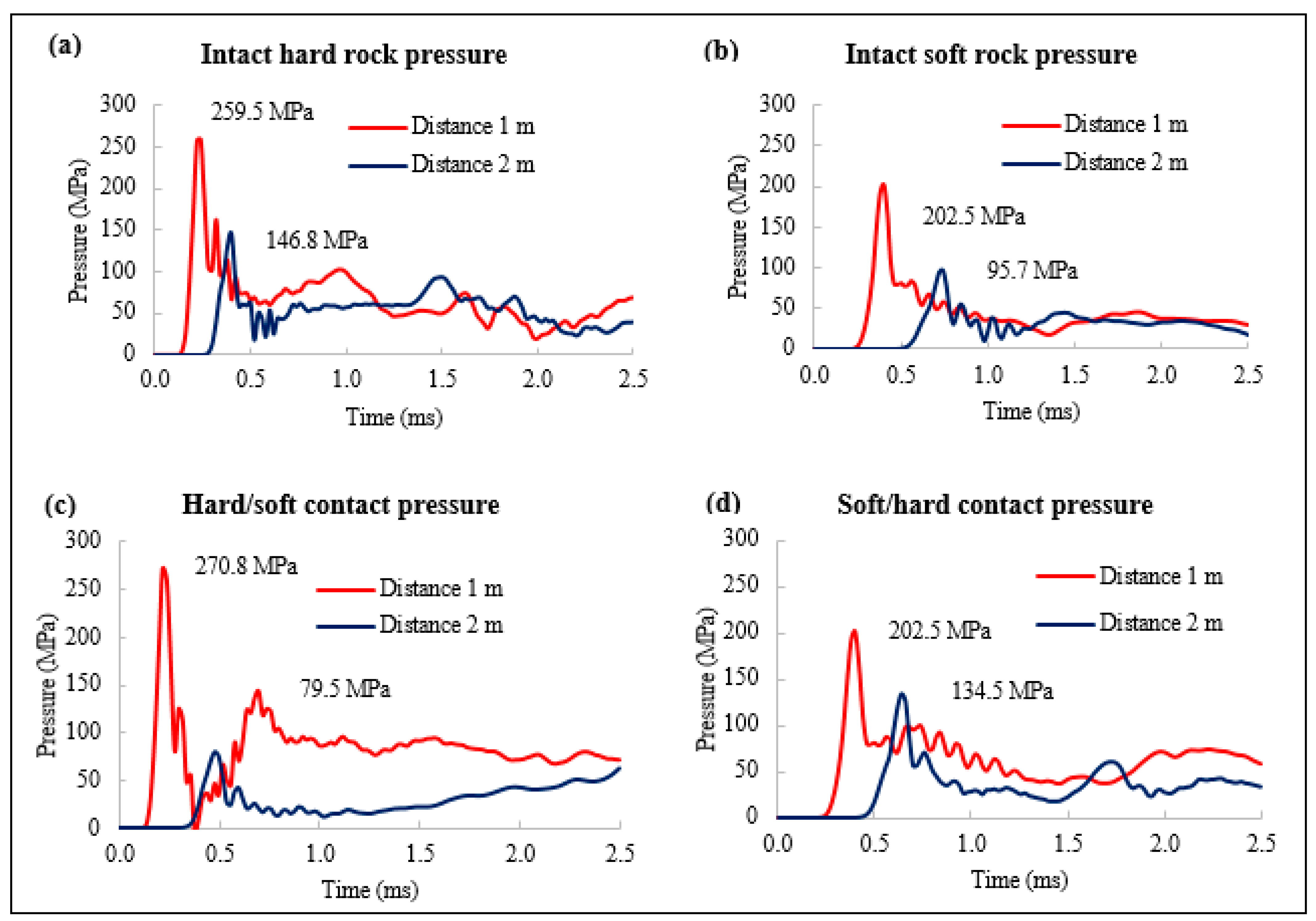
3.2. Stress Wave Interaction Across Contacts
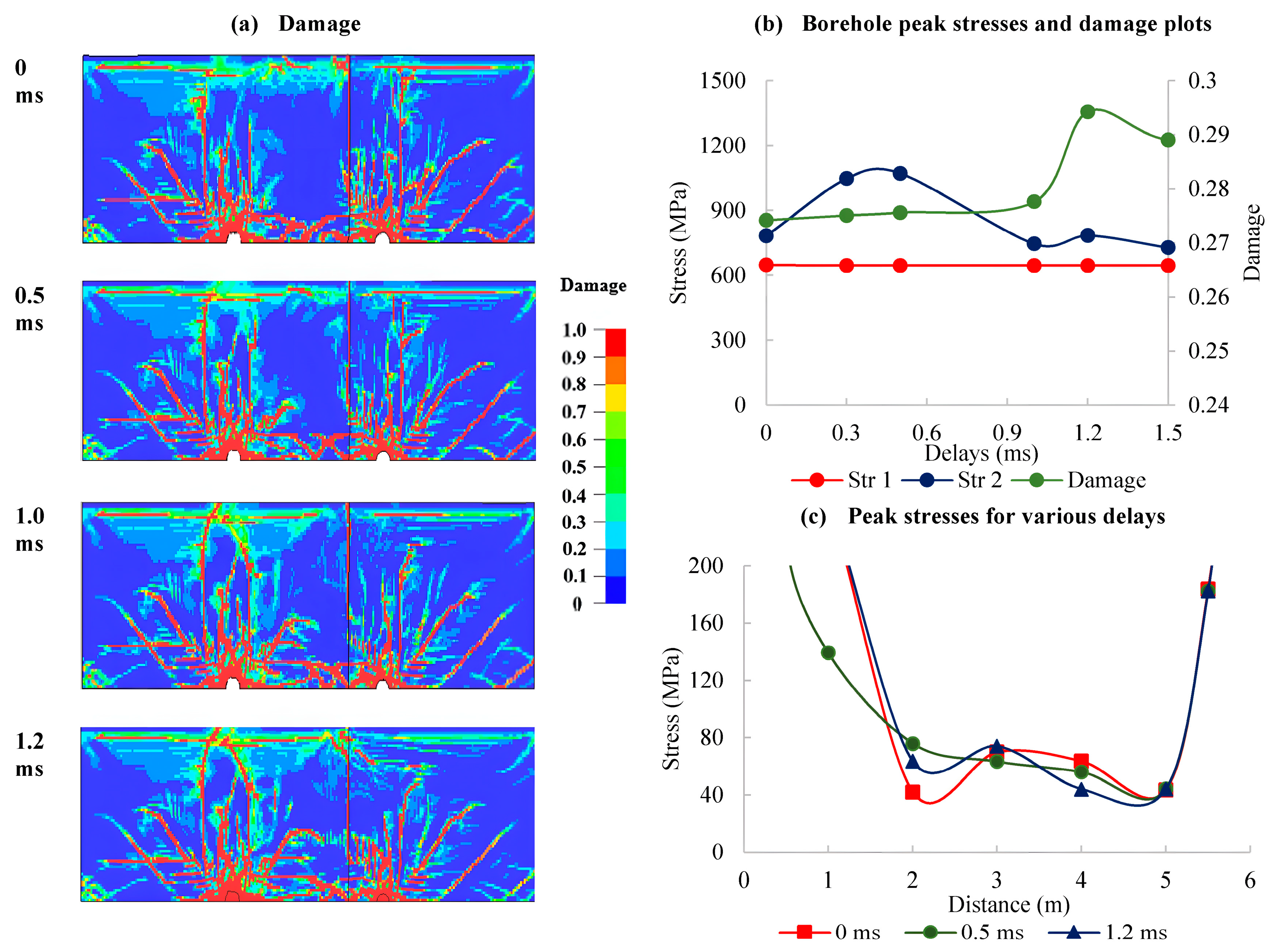
3.3. Stress Wave Interaction Across the Joint
3.3.1. Clay Infill
3.3.2. Empty Joints
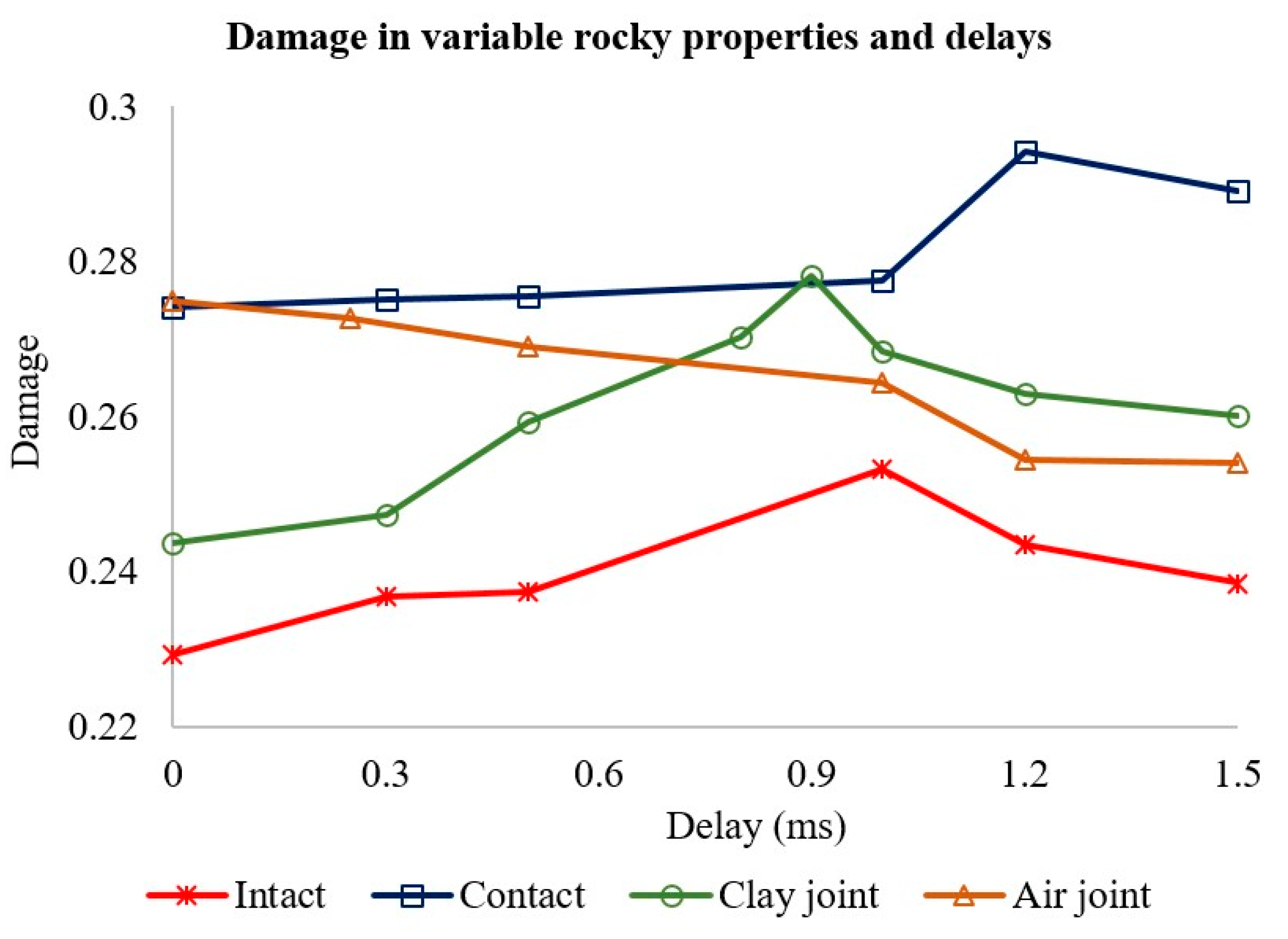
4. Discussion and Application in the Blasting
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, Z.; Mohanty, B.; Xie, H. Numerical investigation of blasting-induced crack initiation and propagation in rocks. Int. J. Rock Mech. Min. Sci. 2007, 44, 412–424. [Google Scholar] [CrossRef]
- Müller, B.; Hausmann, J.; Niedzwiedz, H. Prediction and minimisation of vibrations during production blasts. In Vibrations from Blasting; Spathis, A., Noy, M.J., Eds.; CRC Press: Boca Raton, FL, USA, 2009; p. 47. [Google Scholar]
- Persson, P.A.; Holmberg, R.; Lee, J. Rock Blasting and Explosives Engineering; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Wilbur, I.D. RI 6151 Vibrations from Instantaneous and Millisecond-Delayed Quarry Blasts; The National Institute for Occupational Safety and Health (NIOSH): Washington, DC, USA, 1963.
- Katsabanis, P.D.; Tawadrous, A.; Braun, C.; Kennedy, C. Timing effects on the fragmentation of small scale blocks of granodiorite. Fragblast 2006, 10, 83–93. [Google Scholar] [CrossRef]
- Rossmanith, H.P. The Use of Lagrange Diagrams in Precise Initiation Blasting. Part I: Two Interacting Blastholes. Fragblast 2002, 6, 104–136. [Google Scholar] [CrossRef]
- Vanbrabant, F.; Espinosa, A. Impact of short delays sequence on fragmentation by means of electronic detonators: Theoretical concepts and field validation. Fragblast 2006, 8, 326–331. [Google Scholar]
- Yi, C.; Johansson, D.; Nyberg, U.; Beyglou, A. Stress Wave Interaction Between Two Adjacent Blast Holes. Rock Mech. Rock Eng. 2016, 49, 1803–1812. [Google Scholar] [CrossRef]
- Yi, C.; Sjöberg, J.; Johansson, D.; Petropoulos, N. A numerical study of the impact of short delays on rock fragmentation. Int. J. Rock Mech. Min. Sci. 2017, 100, 250–254. [Google Scholar] [CrossRef]
- Johansson, D.; Ouchterlony, F. Shock Wave Interactions in Rock Blasting: The Use of Short Delays to Improve Fragmentation in Model-Scale. Rock Mech. Rock Eng. 2013, 46, 1–18. [Google Scholar] [CrossRef]
- Stagg, M.S.; Rholl, S.A. Effects of accurate delays on fragmentation for single-row blasting in a 6.7 m (22 ft) bench. In Proceedings of the Second International Symposium on Rock Fragmentation by Blasting, Keystone, CO, USA, 23–26 August 1987; pp. 210–223. [Google Scholar]
- Saadatmand Hashemi, A.; Katsabanis, P. The Effect of Stress Wave Interaction and Delay Timing on Blast-Induced Rock Damage and Fragmentation. Rock Mech. Rock Eng. 2020, 53, 2327–2346. [Google Scholar] [CrossRef]
- Dotto, M.; Pourrahimian, Y.; Joseph, T.; Apel, D. Assessment of blast energy usage and induced rock damage in hard rock surface mines. CIM J. 2022, 13, 166–180. [Google Scholar] [CrossRef]
- Zhang, Z.X. Rock Fracture and Blasting: Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Fan, L.F.; Wang, L.J.; Wu, Z.J. Wave transmission across linearly jointed complex rock masses. Int. J. Rock Mech. Min. Sci. 2018, 112, 193–200. [Google Scholar] [CrossRef]
- Dotto, M.S.; Apel, D.; Pourrahimian, Y. Investigating the influence of discontinuity parameters on blast-induced fragmentation. Int. J. Min. Reclam. Environ. 2024, 38, 745–769. [Google Scholar] [CrossRef]
- Wang, J.; Yin, Y.; Esmaieli, K. Numerical simulations of rock blasting damage based on laboratory-scale experiments. J. Geophys. Eng. 2018, 15, 2399–2417. [Google Scholar] [CrossRef]
- Dotto, M.S.; Pourrahimian, Y. The Influence of Explosive and Rock Mass Properties on Blast Damage in a Single-Hole Blasting. Mining 2024, 4, 168–188. [Google Scholar] [CrossRef]
- Müller, B. Adapting blasting technologies to the characteristics of rock masses in order to improve blasting results and reduce blasting vibrations. Fragblast 1997, 1, 361–378. [Google Scholar] [CrossRef]
- Sim, Y.; Cho, G.-C.; Song, K.-I. Prediction of Fragmentation Zone Induced by Blasting in Rock. Rock Mech. Rock Eng. 2017, 50, 2177–2192. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, Y.; Xiong, F. Three-Dimensional Numerical Analysis of Blast-Induced Damage Characteristics of the Intact and Jointed Rockmass. Comput. Mater. Contin. 2019, 60, 1189–1206. [Google Scholar] [CrossRef]
- Borrvall, T.; Riedel, W. The RHT concrete model in LS-DYNA. In Proceedings of the 8th European LS-DYNA Users Conference, Strasbourg, Austria, 23 May 2011; pp. 23–24. [Google Scholar]
- Jiang, X.; Xue, Y.; Kong, F.; Gong, H.; Fu, Y.; Zhang, W. Dynamic responses and damage mechanism of rock with discontinuity subjected to confining stresses and blasting loads. Int. J. Impact Eng. 2023, 172, 104404. [Google Scholar] [CrossRef]
- Dotto, M.S.; Pourrahimian, Y. The effects of rock mass properties on explosive energy in rock blasting. In Proceedings of the Application of Computers and Operations Research in the Mineral Industry (APCOM), Rapid City, SD, USA, 28 June 2023; Society of Mining. Metallurgy & Exploration (SME): Englewood, CO, USA, 2023. [Google Scholar]
- Xie, L.X.; Lu, W.B.; Zhang, Q.B.; Jiang, Q.H.; Chen, M.; Zhao, J. Analysis of damage mechanisms and optimization of cut blasting design under high in-situ stresses. Tunn. Undergr. Space Technol. 2017, 66, 19–33. [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation (LSTC). LS-DYNA Keyword User’s Manual R11 Volume II Material Models 2018. Available online: https://www.dynasupport.com/manuals/ls-dyna-manuals/ls-dyna_manual_volume_ii_r11.pdf (accessed on 15 June 2023).
- Riedel, W.; Thoma, K.; Hiermaier, S.; Schmolinske, E. Penetration of Reinforced Concrete by BETA-B-500 Numerical Analysis using a New Macroscopic Concrete Model for Hydrocodes. In Proceedings of the 9th International Symposiumon Interaction of the Effects of Munitions with Structures, Berlin, Germany, 3 May 1999; pp. 315–322. [Google Scholar]
- Lee, E.L.; Hornig, H.C.; Kury, J.W. Adiabatic Expansion of High Explosive Detonation Products; Contract No.: UCRL-50422; University of California Radiation Lab.: Livermore, CA, USA, 1968. [Google Scholar]
- ORICA. Technical Data Sheet—Fortis Extra System—Africa. 2018. Available online: https://www.oricaminingservices.com/ca/en/product/products_and_services/bulk_systems/fortis_extra/122 (accessed on 25 June 2020).
- Hansson, H. Determination of Properties for Emulsion Explosives Using Cylinder Expansion Tests and Numerical Simulation; Engineering, Materials Science: Stockholm, Sweden, 2009. [Google Scholar]
- Tang, H.-L.; Liu, X.; Yang, J.; Yu, Q. Experimental Study on the Influence of Delay Time on Rock Fragmentation in Bench Blasting. Appl. Sci. 2023, 13, 85. [Google Scholar]
- Jeong, H.; Jeon, S. Characteristic of size distribution rock chip produced by rock cutting with a pick cutter. Geomech. Eng. 2018, 15, 811–822. [Google Scholar] [CrossRef]










| Rock Property (Units) | Density (g/cm3) | UCS (MPa) | Tensile Strength (MPa) | Young Modulus (GPa) | Poisson Ratio |
|---|---|---|---|---|---|
| Value | 2680 | 126.02 | 14 | 90.8 | 0.24 |
| Explosive Property (Units) | Density (g/cm3) | Minimum Diameter (mm) | VOD (km/s) | Bulk Energy (MJ/kg) |
|---|---|---|---|---|
| Value | 1.10–1.25 | 64 | 4.1–6.7 | 3.47–4.35 |
| Explosive Type | Density (kg/m3) | VOD (m/s) | Pcj (GPa) | A (GPa) | B (GPa) | R1 | R2 | ω | Eo (kJ/cm3) | vo |
|---|---|---|---|---|---|---|---|---|---|---|
| E682 | 1207 | 4789 | 6.926 | 276.2 | 8.44 | 5.2 | 2.1 | 0.5 | 3.87 | 0 |
| Density (kg/m3) | UCS (MPa) | Tensile Strength (MPa) | Young Modulus (GPa) | Poisson Ratio | P-Wave Velocity (m/s) |
|---|---|---|---|---|---|
| 2400 | 88 | 0.1 × UCS | 25 | 0.3 | 2589 |
| Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | Yield Stress, (MPa) | Tangent Modulus, (GPa) | Hardening Parameter | Failure Strain, FS |
|---|---|---|---|---|---|---|
| 1160 | 5 | 0.35 | 0.4 | 4 | 0 | 0.5 |
| Density (kg/m3) | C4 | C5 | C6 | Eo (MPa) | Vo |
|---|---|---|---|---|---|
| 1.29 | 0.4 | 0.4 | 0 | 0.5 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dotto, M.S.; Pourrahimian, Y. The Effect of Initiation Time Delay and Sequencing on Rock Damage in Multi-Hole Blasting. Mining 2025, 5, 22. https://doi.org/10.3390/mining5020022
Dotto MS, Pourrahimian Y. The Effect of Initiation Time Delay and Sequencing on Rock Damage in Multi-Hole Blasting. Mining. 2025; 5(2):22. https://doi.org/10.3390/mining5020022
Chicago/Turabian StyleDotto, Magreth Sungwa, and Yashar Pourrahimian. 2025. "The Effect of Initiation Time Delay and Sequencing on Rock Damage in Multi-Hole Blasting" Mining 5, no. 2: 22. https://doi.org/10.3390/mining5020022
APA StyleDotto, M. S., & Pourrahimian, Y. (2025). The Effect of Initiation Time Delay and Sequencing on Rock Damage in Multi-Hole Blasting. Mining, 5(2), 22. https://doi.org/10.3390/mining5020022







