Abstract
The difficulty of effectively planning and assigning weekly activities has a significant influence on the long-term productivity of an underground mine. It is an especially difficult task to choose the best places for operations inside an underground gold mine. It cannot be resolved by only selecting the levels with the highest grade of ore because the underground mine’s ore transport network has a range of capacity limitations that may prohibit the immediate mining of all the levels with the highest grade. To solve this scheduling difficulty, we formulated a new mixed-integer network flow model of the problem of weekly allocating mining operations in an underground gold mine such that the total gold mined (in ounces) was maximized subject to the transportation capacity constraints. The model was applied to an underground gold mine in Red Lake, Ontario, Canada. The results were compared to those of two greedy heuristic models that were designed to represent the decision-making heuristics that are currently used at the mine. It was found that the new model yielded solutions that improved upon the two greedy heuristics by 14.7% and 6.0%, respectively. The results of this research illustrate that the development of this optimization model can support decisions to improve a gold mine’s productivity.
1. Introduction
In underground mines, the problem of scheduling the weekly locations of mining operations has a major impact on the productivity of the entire mining operation [1]. The objective of the weekly schedule is to maximize production within the constraints of the mine’s strategic and tactical plans. Optimization of the weekly schedule is difficult to optimize for two reasons. First, the solution (i.e., the optimal locations selected to mine over the next weekly period) is constrained by the feasibility of transporting the mined material from the selected locations, through the capacity-constrained transportation network, to the surface. The transportation network in an underground mine has strict capacity constraints on the mass of material that can move, per unit time, through many links within its transportation network. The second reason this problem is difficult to solve optimally is that commercial software is currently not available for such a planning problem in underground gold mines. There is no general-purpose software package that has been designed to represent realistically the diversity of constraints peculiar to the many underground mine types—including underground gold mines. As a result, planners are forced to resort to using ‘rules of thumb’ to solve this problem.
In underground gold mines in particular, the operational planning problem of scheduling the weekly locations of mining operations, subject to transportation constraints, has, to our knowledge, not been formulated as an optimization model at the operational scale of planning. The problem has therefore been solved using ‘rules of thumb’ (i.e., heuristics) typically executed on a spreadsheet. Finding an optimal rather than a heuristic solution to this problem is important for two reasons. First, the difference between an optimal and a heuristic solution may have major differences in the objective function value of the problem’s solution; i.e., the mine’s operational productivity, measured in ounces of gold delivered to the surface per day. This is because, in a gold mine, the grade of the gold-ore (measured in g/tonne) varies from location to location. In other words, the value of the locations selected for mining can vary greatly because of the variance of grade across space, in an underground gold mine. Hence, if this were, for example, a coal mine (e.g., [2]), the difference between a heuristic and an optimal solution to this problem may not be great, because the value of the grades at each selected location differ less significantly than in a gold mine. Since this is a gold mine, the value of the optimal feasible solution is highly sensitive to slight differences in the locations selected for mining. Therefore, the difference between an optimal and a heuristic solution to this problem may be quite important economically. A second reason for the importance of using an optimization model on this problem is that the above-ground processing facilities are constrained, in their daily productivity, by the value of the gold ore that is delivered to the surface each day. Since the value of the gold ore delivered to the surface each day is the objective function of this operational problem’s optimization model, the solution to this problem has a direct impact on the productivity of the above-ground processing facilities. In other words, the solution to this problem, when seen in a broader context, can be seen to act as a constraint on the economic productivity of the entire mining facility itself.
The objective of this paper is to formulate and evaluate a new operational planning model for the underground gold mining problem of scheduling the weekly and optimal location of mining operations, subject to transportation constraints on the flow of material. The formulation will be of a mixed-integer, network-flow model. This model will be applied to a case study at the Red Lake Gold Mine in Ontario, Canada. The model will be evaluated by comparing its solution to that of a greedy heuristic currently used. In this way, we will evaluate a larger question: whether the benefit of using a specific operational planning model, for constraints peculiar to underground gold mine, is of any economic consequence.
The outline of this paper is as follows: first, a literature review is presented; second, the formulation of the new model and the heuristic algorithm are presented in the Methods; third, the case study, Red Lake Gold Mine, is described; fourth, the results are presented, in which the optimal solution is compared to the heuristic solution; and finally, a discussion of the paper’s results and their significance is evaluated.
2. Literature Review
Literature reviews on the use of operations research in mining in general (e.g., [3,4,5]), and underground mining in particular [6], indicate that: while there is a wealth of research in the development of optimization models for strategic and tactical problems in mining, published work on scheduling models used at the operational scale has been much more scarce. The literature to be reviewed on this problem is therefore brief and shows a great diversity of models formulated for operational production planning. For this reason, the review is presented chronologically, not thematically.
Nehring, Topal, and Knights [7] developed a model for a sub-level stopping mine, which was used to solve the problem of scheduling and allocating machines for the transportation of extracted ore from the draw-points, via intermediate storage, to a haulage shaft. The model also included decisions on a second-stage movement of ore; i.e., transporting ore from an ore-pass to a crusher. The problem was formulated as a mixed-integer programming (MIP) model to allocate machines to different draw-points, on a shift basis, over a period of 2 months. The objective function of the model was to minimize the deviation from production targets subject to constraints on machines and crew. The model’s solutions were evaluated on a simulated mine.
Martinez and Newman [8] developed a comprehensive operational scheduling and allocation model for an iron ore mine in Northern Sweden. The model minimized deviations from monthly production targets subject to a host of operational constraints, many of which were peculiar to sub-level caving. The MIP model was solved on a real-world dataset, using a heuristic algorithm, to within 5% of production targets.
Howes and Forrest [9] described an approach to improving operational decision making at a mine in Bulgaria. A key strategy introduced in this work was short interval control. This involves the use of real-time production information to provide a central monitoring and control room with the real-time status of all tasks in the mine. This comprehensive communications infrastructure was designed to support key frontline decision making on operational resource allocation achieving the maximum efficiency for each shift. At present, the decisions are made by management in the central control room, but the development of operations research models to support management decisions in this environment is the next step in the evolution of this ambitious project, and therefore, it is a fruitful field of future research on operational scheduling in mining.
Nehring et al. [10] addressed the task of integrating short- and medium-term production plans. Their method was to combine the short-term objective of minimizing deviation from targeted mill feed grade with the medium-term objective of maximizing the net present value (NPV) into a single mathematical optimization model. Their short-term problem was not constrained by capacities on the transportation network. Their resulting solution was a global optimum of the two planning problems.
Little, Knights, and Topal [11]) evaluated the advantage of simultaneously integrating decisions on both stope layout and production scheduling into one model. They found that the solutions generated by the integrated model were superior to those using different models sequentially. The benefits of integrating separate but interdependent models, as demonstrated by these authors, are promising.
Schulze et al. [12] scheduled a mobile production fleet in an underground, room-and-pillar, potash mine. The objective of the model was to minimize the make-span, i.e., to create the shortest logical project schedule, by efficiently using project resources and adding the lowest number of additional resources to each sub-task. The problem was formulated as an MIP model and solved using a commercial solver. The authors continued to explore the room and pillar-scheduling problem by developing a heuristic solution method in Schulze and Zimmermann [13].
Campeau and Gamache [14] presented an optimization model for the short-term scheduling of excavation, hauling, and backfilling activities at a cut-and-fill gold mine in Canada. The objective function was to maximize the total discounted tonnage extracted over an eighteen-week planning horizon, subject to resource and sequencing constraints. The authors observe that the real value of their solutions rests heavily on the quality of the tactical plan’s selected sequence of blocks, on which their model acts.
Manriquez et al. [15] developed a simulation–optimization model to generate short-term production schedules for improving schedule adherence using an iterative approach. In each iteration of this framework, a short-term schedule was generated using a mixed-integer linear programming model that is simulated later using a discrete-event simulation model. The model was not subject to capacity constraints on the transportation network.
From this review of the literature, one can draw two observations. First, the problems modeled for operational planning in underground mines are not generic but quite diverse and specific to mine types. The models formulated were often custom-built for the particular extraction method of the mine and its design. It is perhaps for this reason that there exists no commercial optimization software that is universally employable for operational scheduling in all underground mines, as there is for tactical planning of underground mines [3]. A second observation that can be drawn from the literature review is that the particular problem addressed in this paper (i.e., the optimal operational-scale scheduling of gold ore and waste flow, in an underground gold mine) has not been addressed within prior research.
3. Methods
The Methods is divided into 4 parts. First, a description of the problem, with a conceptual figure, is given; second, the mathematical formulation of the optimization model is presented; third, the heuristic algorithm used in this paper, to represent the current decision-making procedure at the mine, is given. Finally, the case study and data used are described.
3.1. Description of Modeled Problem
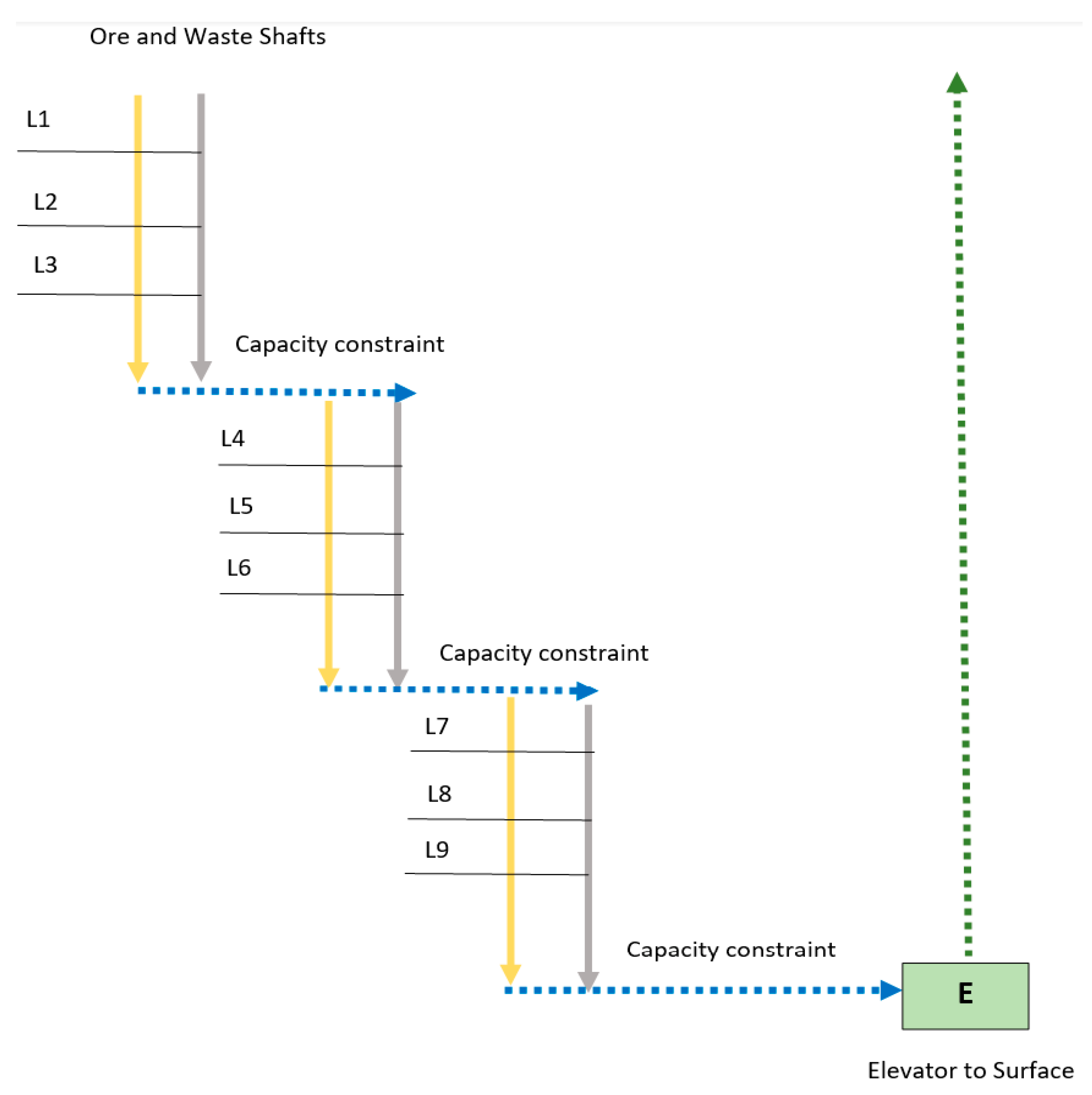
A conceptual figure of the problem is presented in Figure 1. Here, we observe a simplified representation of an underground gold mine. First, observe that there are 9 levels. Each level may have a different: (i) grade of ore (g/tonne); (ii) mass of ore that may be removed daily (tonnes/day); and (iii) mass of waste that must be removed if ore is removed (tonnes/day). These are the network’s source nodes. Second, observe that there are two types of shafts for the downward movement of mined material: ore and waste shafts.
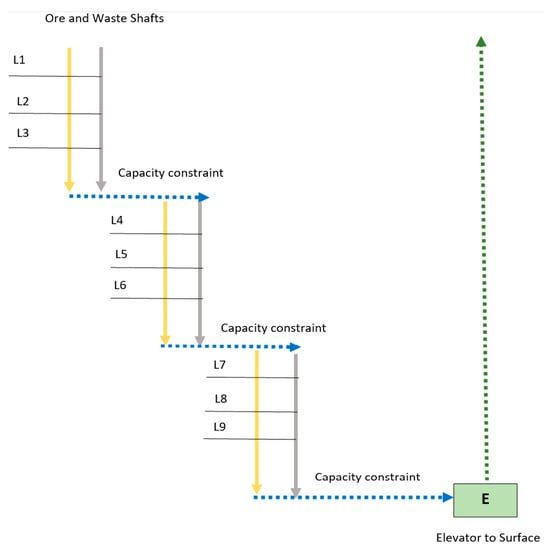
Figure 1.
Conceptual figure of the modeled problem.
There are no capacity constraints on these shafts. Third, observe that at the bottom each shaft, the horizontal transportation of both materials occurs. This horizontal transportation has a daily capacity constraint. The shafts and horizontal transportation arcs are the network’s trans-shipment arcs. Fourth, observe that at the end of the network, there is a capacity-constrained elevator to the surface. This is the network’s terminal node where there is a daily demand for ore and a daily demand for the mass of waste resulting from the mining of the ore. Hence, the problem may be summarized as: select a set of levels for daily operation such that the mass of gold removed (in ounces) is maximized, subject to: (i) capacity constraints on ore transportation (tonnes per shift); (ii) daily ore targets at the above-ground processing facility (in tonnes) are met; and (iii) the waste material accompanying ore removal is removed. The problem is formulated as a network flow model where each level is a supply node and the elevator is the demand node. Constraints on the flow of material occur at transition nodes. Unless these transportation capacity constraints are used in planning, the movement of both ore and waste through the mine could be stopped during a shift because a transportation corridor may become backed-up from crews trying to move too much ore through a corridor, with too little capacity for such a quantity, within the planned period. In addition, the selection of a level must be represented by a binary decision variable because if real numbers were used, a solution with tiny, fractional mining of levels could occur. This is not feasible in practice because the fractions might be very small, and therefore, a solution could be produced where it is not worth sending machines and a crew to mine a level with a tiny, fractional amount of ore. Finally, the daily schedule of production is to be found for a planning horizon of 7 days.
This problem is difficult to solve, for it is a combinatorial optimization problem that may be reduced to the famous knapsack problem. In the knapsack problem, one is given a set of items, each with a weight and a value, and one must select a set of items to include in a knapsack such that (i) the total weight is less than or equal to a given limit; and (ii) the total value of the contents of the knapsack is as large as possible [16]. The operational mining problem described above can be reduced to the knapsack problem because apart from the transportation constraints, the problem is the same; that is, selecting a set of levels so that the total mass of ore selected is less than or equal to the limit set by the elevator’s capacity and the objective is that the total value of the gold (in ounces) from the levels selected for mining be as valuable as possible.
3.2. Formulation of the New Model
The mathematical formulation of the model is presented below.
| Indices and Sets | |
| n, N | index and set of levels in the mine. |
| t, T | index and set of planning periods. |
| m, M | index and set of materials moved through the network (i.e., ore or waste material). |
| i, j, J | index and set of nodes in the network. |
| B | set of intermediate (transshipment) nodes. |
| C | set of arcs with capacity constraints. |
| Dij | capacity on arc i–j (tonnes per day). |
| On | set of arcs flowing out from node on level n. |
| In | set of arcs flowing into node on level n. |
| F | the set of arcs flowing into network’s terminal node. |
| Parameters | |
| smn | mass of material type, m, available for removal at level n of the mine (tonnes). |
| gn | estimated mass of gold ore available at level n of the mine (grams). |
| Decision Variables | |
| ynt | 1 if material is removed from level n in period t, 0 otherwise. |
| xijmt | flow of material, m, through arc i–j, in period t (tonnes). |
Objective Function:
Maximize total mass of gold removed (in grams) over all periods
Subject to:
- -
- Mine each level not more than once.
- -
- If a level is mined, it is a source of ore and waste material flow.
- -
- Transition nodes defined.
- -
- Terminal node defined.
- -
- Capacity constraints.
- -
- Binary and non-negativity constraints.
The objective Function (1) of the model is to maximize the total mass of gold removed (in ounces) during the daily shift. The mass of gold is based on the tactical plan’s estimated grade of each block at each level (measured in grams per tonne) and the total mass of gold ore and waste (measured in tonnes) that is currently available to be mined at a given level. The first constraint (2) ensures that no level may be mined more than once over the planning horizon. The second constraint (3) defines the potential sources of flow through the network. This constraint ensures that if a given level, n, is mined in period t, then each material type, m, will flow out of the node on this level and into the network. Note that the flow of each material type (ore and waste) is tracked separately from each source. Constraint (4) is a standard flow balance equation for transition nodes in a network model. Equation (5) defines the terminal node and the mass of each material type demanded at the terminal node. Note that the total mass of each material type refers to the total mass of each material type that was mined during each period. There is an upper bound on this value implicit in the capacity constraint on the arc connected to the terminal node. Equation (6) defines the capacity constraints on the flow of material types imposed on the set of arcs with capacity constraints. Equation (7) ensures that the decision variable, ynt, is binary. This variable is binary for two reasons. First, the mass of material removed from each level must be discrete; otherwise, the model might produce solutions that are operationally infeasible (e.g., tiny masses of material to be scheduled for removal from a level). Second, the binary decision variable is needed to trigger the flow in Equation (3). Equation (8) ensures that a negative flow value is not possible.
3.3. Description of Heuristic Algorithm
Given the absence of an optimization model to solve this operational problem, our industrial partner had been using a heuristic method (i.e., rules of thumb). This method will now be described, for its results will be compared with the results of the new optimization model in order to evaluate the latter.
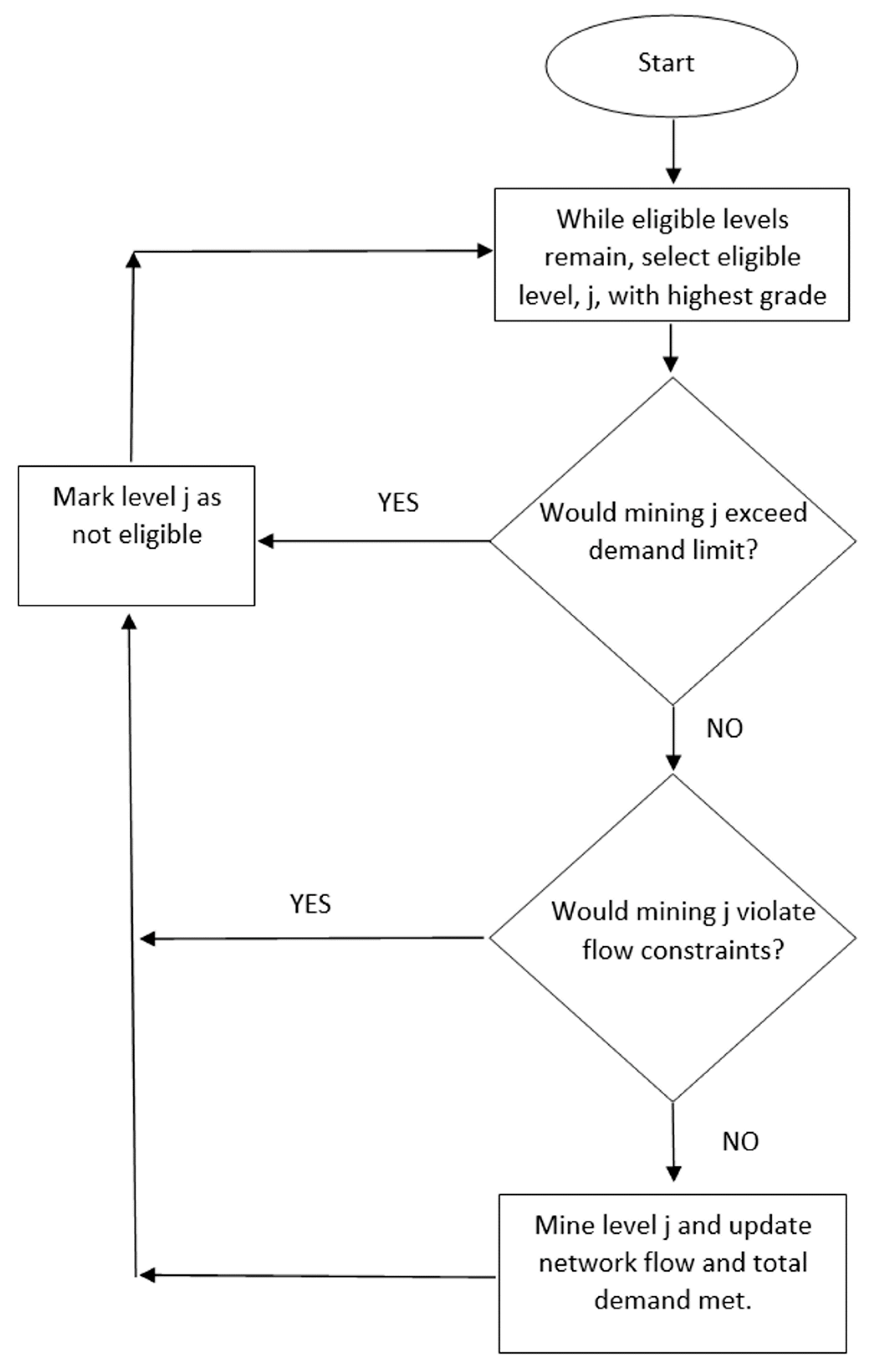
Given that the objective function of the model is maximize the gold ounces removed over the planning horizon, subject to capacity constraints, a greedy search was used. A greedy search heuristic has been used quite successfully on many versions of the knapsack model [17]. In this greedy search, the levels were sorted from highest to lowest grade, and selection proceeds from highest to lowest, subject to whether the addition of a level to the schedule violates the transportation capacity constraints of in the mine (see Equation (6) above). An algorithmic flowchart of the greedy search is presented in Figure 2 (below). Here, the search is repeated at the start each of the 7 days, and all candidate levels are rendered eligible for inclusion in the schedule at the start of each day.
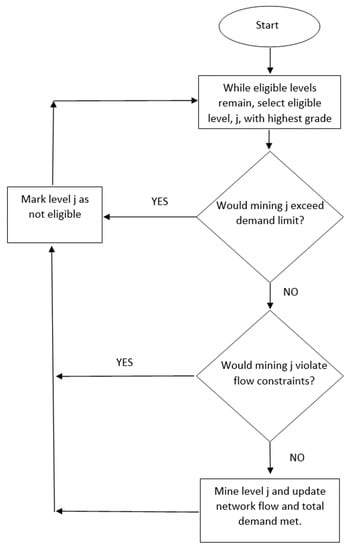
Figure 2.
Algorithmic flowchart of greedy heuristic.
In the greedy heuristic described above, there is a demand limit on two types of materials mined: gold ore and waste. In addition, a second heuristic is used in the paper, which is called heuristic 2. Heuristic 2 places a demand limit only on the ore and allows the mass of waste to exceed its target. Heuristic 2, therefore, allows for greater opportunity to maximize the value of the objective function while running the risk of mining a slight excess of waste. Heuristic 2 is sometimes used by the planners at Red Lake. Hence, the trade-off involved in using heuristic 1 versus heuristic 2 is a practical one for decision makers to explore and use. In this paper, both heuristic 1 and heuristic 2 are used, and their results are presented and compared with the results of the new optimization model.
3.4. Description of Case Study
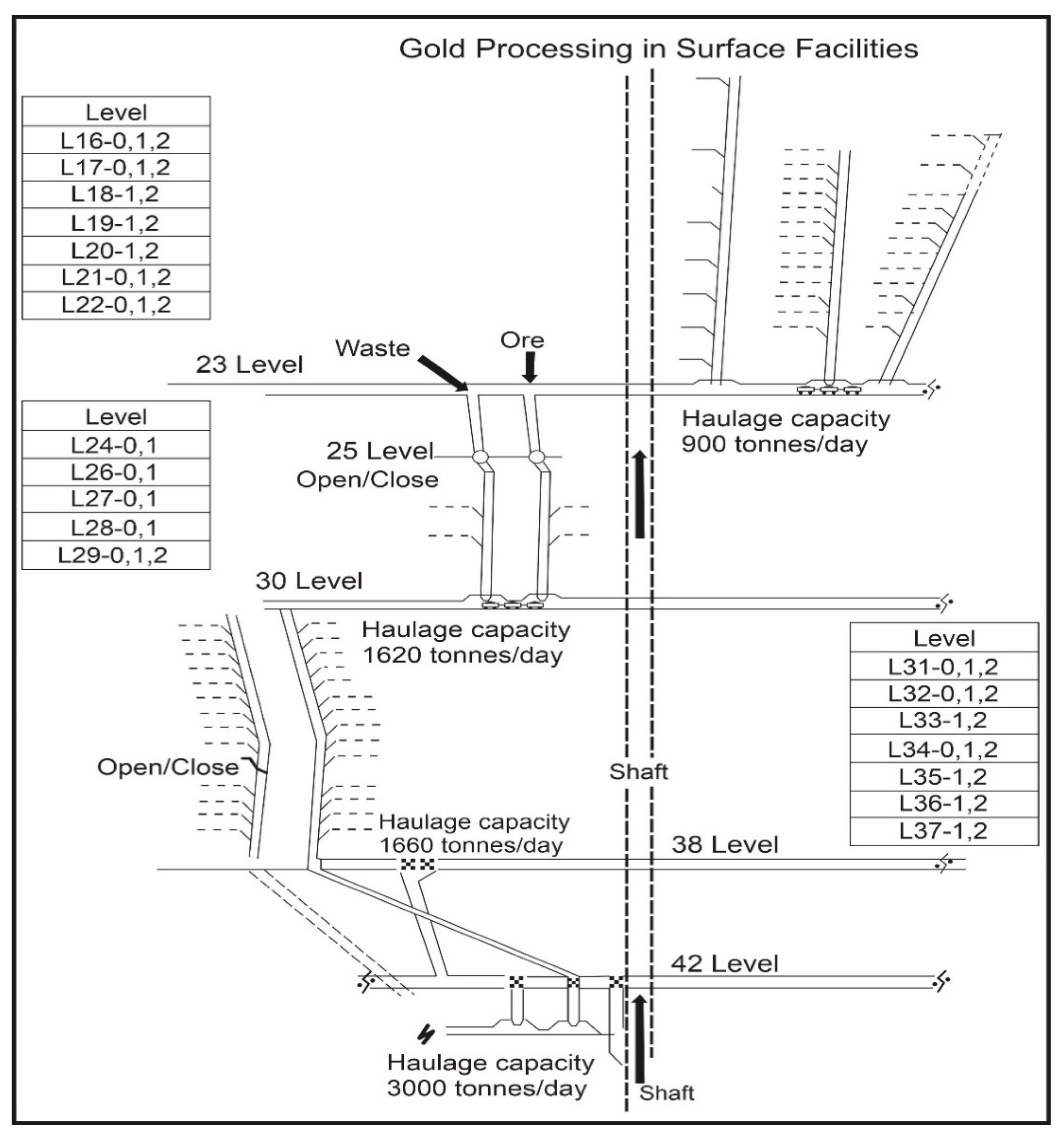
The case study is the Red Lake underground gold mine, which is located in Red Lake, Ontario, Canada. The mine is approximately 50 years old and is currently under the management of Newmont-Goldcorp Corporation, our industrial partner. The levels of production are shown in Figure 3 (below). Each level contains discrete masses of both ore and waste material. Based on data shared with us by our industrial partner, the mass of each block, in each level ranges from 3500 to 5000 tonnes. Each block has been scheduled, in the tactical plan, for mining within the calendar year. The objective of this model is to transform the annual tactical plan into an optimal weekly operational plan of production. There are 19 levels currently eligible for production based on the tactical plan.
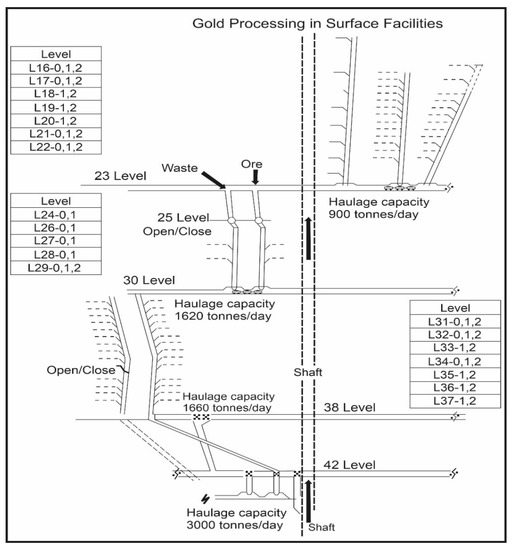
Figure 3.
Underground mine at Red Lake, Ontario, Canada.
The levels scheduled for tactical operation at the Red Lake gold mine are presented in Figure 3 (below). First, observe that there are three sets of levels. Second, observe that at the bottom of the ore and waste shafts of each level, the horizontal transportation of material is required, and there is a daily haulage capacity constraint on this. Third, observe that at the bottom of the mine, there is an elevator to the surface with a daily capacity of 3000 tonnes/day. The daily demand at the surface is for 2000 tonnes of gold ore and 1000 tonnes of waste to be sent to the surface daily.
Each block at each level at Red Lake differs by: (i) the grade of the ore (g/tonne); (ii) the mass of ore that can be removed in one day (tonnes/day); and (iii) the mass of waste that must be removed in one day (tonnes/day), if ore is removed. The values for these parameters are presented in Table 1. It should be noted that the parameters in Table 1 for the grade of ore are not real. Our industrial partner, understandably, wished to keep these values on grade private. The parameters for the grade of ore were therefore generated using a random number generator such that each level was randomly assigned (with equal probability) a grade between 5 and 15 g of gold per tonne of ore. This range of grades is realistic for a typical gold mine, and the fact that the values assigned are not real does not compromise the evaluation of our optimization model.

Table 1.
Ore and waste values at each level of the case study.
The optimization model was built using MPL®software (Maximal Software Inc, Arlington, VA, USA) and solved using the branch and bound algorithm of CPLEX® 12.0 (IBM Corporate, Armonk, NY, USA) on a Windows 10 operating system using an Intel CORE i7 CPU (Intel Corporation, Santa Clara, CA, USA). The model had 133 binary decision variables and 226 continuous flow variables. All instances were solved in less than 30 s.
4. Results
The objective function values resulting from the application of the optimization and greedy heuristic models to the case study are presented in Table 2 (below).

Table 2.
Results of the optimization and greedy heuristic models compared.
Table 2 yields several observations. First, the objective function (i.e., maximize gold ounces mined per day) of the optimization model is greater than the objective functions of both greedy heuristics: it is 14.7% higher than greedy heuristic 1 and 6.0% higher than greedy heuristic 2. These results indicate the benefit of formulating and using an optimization model for solving this problem versus using the current greedy heuristic. Second, Table 2 also shows that greedy heuristic 2 achieved a higher objective function than greedy heuristic 1 by exceeding its waste limit (of 1000 tonnes/day) by 7 tonnes per day; and that, even after exceeding its waste limit, the objective function of greedy heuristic 2 was 6% lower than that of the optimization model. These results therefore show that the value of a solution to this problem depends not only on the optimal removal of gold ore alone but also on the optimal removal of ore and waste simultaneously. Third, Table 2 also shows that the solution of the optimization model came closest to maximizing the capacity of the network’s final node (i.e., 3000 tonne/day capacity of the elevator carrying material to the surface). This can be seen by the values under the total tonnes removed per day where the optimization model’s solution used 96.5% of the capacity, while greedy heuristic 1 used only 73.8% and greedy heuristic 2 used 90.3%. These differences in capacities used show the importance, in this problem, of packing the elevator to the surface as closely to its capacity as is possible by using an optimization model based on the knapsack model.
The solutions of the optimization model and greedy heuristics are presented in Table 3.

Table 3.
The solutions of the optimization model and greedy heuristics.
Table 3 presents the locations of the levels selected for mining, in each day. Note that the selected blocks at each level did not change over the days of scheduling because of their great magnitude (in tonnes) relative to magnitude (in tonnes) of material removed daily. Table 3 yields three observations worthy of note. First, one can observe the effect of the first flow constraint (between levels 29 and 31 as shown in Figure 3), of 1800 tonnes of total material flow per day, on the three different solutions. Given the parameters on ore and waste material at each level (in Table 1), one can see that the solution of the optimization model in Table 3 moved 1606 tonnes of material and 491 ounces of gold from level 29 to 31; and the solution of the greedy heuristic moved 1689 tonnes of material and 468 ounces of gold. Hence, the capacities between levels 29 and 31 was more closely met by the greedy heuristic than by the optimization model. This difference indicates that the optimal solution does not need to maximize the flow of material or gold through this capacity constraint (between levels 29 and 31) as it does through the final capacity constraint (after level 37). Hence, in this model of the problem, the final capacity constraint alone functions as a knapsack constraint, i.e., a constraint by which as much gold as possible must flow subject to a capacity limit on total flow of material (tonnes/day).
Second, Table 3 shows that the optimal solution contains levels of a lower grade of ore than the solutions of the greedy heuristics. The average grade of ore for the levels selected in the optimal is 10.8 g/tonne, while the average grade per level for the solutions of greedy 1 and greedy 2 were 12.3 and 11.9 g/tonne, respectively. The lower grade selected in the optimal solution was facilitated by more closely packing the total material capacity constraint of 3000 tonnes/day, thus enabling the movement of more material and therefore more total gold per day than the greedy heuristics. Hence, the results in Table 3 illustrate how the optimal solution represents a more successful resolution of the trade-off implicit in this problem; viz., the problem of packing as much gold as possible into the terminal node of the network subject to capacity constraints in the transportation network.
Third, from Table 3, one can observe that the optimal solution included more levels to operate on than the heuristic solutions. The optimal solution contained eight levels, while the solutions of greedy heuristic 1 and 2 contained six and seven levels, respectively. The extra level of operation contained in the optimal solution entails a higher operational cost, and the decision-maker must evaluate whether the additional cost of operations is worth the additional flow of gold accompanying this solution. In this case, the trade-off between the optimal solution and the solutions of heuristic 1 and 2 implies that: an increase in gold moved to the surface, by 14.7%, requires an extra 2 levels of operation compared to heuristic 1; and an increase in gold mined, by 6.0%, requires an extra one level operation compared to heuristic 2 (which are also has excess waste mined).
5. Discussion
From the results, we find several points deserving discussion: first, the merit of the greedy heuristic used in this paper; second, the practical benefits of using this model; and finally, some thoughts on the benefits of developing an operational-scale optimization model for underground mining.
First, an evaluation of the greedy heuristic versus the optimization model is required. To do this, it should first be noted that a greedy heuristic has been used, for many decades, to solve multiple versions of the knapsack model [18] and has produced useful results [17]. In other words, by using the greedy heuristic method to provide results with which to compare and evaluate our optimization model, we have not selected a weak and insignificant method. Greedy heuristics have been used, in practice, to solve large instances of the knapsack problem [19]. The operational mine-level scheduling problem modeled in this paper is not likely ever to have a problem instance so large that it will require a greedy heuristic to solve it. This is because the binary decision variable, used in this model, represents a mine’s level; and there would need to be in excess of 5000 mine levels for a problem instance to be computationally infeasible for an optimization model which is NP-hard. Hence, it unlikely that the benefits of using an optimization model instead of a greedy heuristic, to solve the model in this paper, will ever become computationally infeasible.
Second, it should be observed that the results illustrate two practical benefits of using the optimization model instead of the greedy heuristic. The first benefit is the increased value of the objective function. The objective function of the optimization model was 14.7% and 6.0% higher than the objective function of greedy heuristics 1 and 2, respectively. The practical benefit of this is an increase in the mine’s economic productivity. The second benefit is an improved scheduling of waste removal. The results produced by the greedy heuristics show the awkward predicament that arises when a greedy heuristic is used to schedule the removal of both ore and waste; i.e., either underutilization or overutilization of the mine’s transportation capacity occurs when compared to the solution for the optimization model. For example, Table 2 shows that heuristic 1 underutilized the mine’s transportation capacity because it was forced to stop adding levels to be mined when the waste to be moved reached 921 tonnes (i.e., 92% capacity), and this meant that total material (i.e., ore + waste) to be moved reached only 2,213 tonnes (i.e., 74% of capacity). Table 2 also shows that for heuristic 2, the mine’s capacity to remove waste was slightly exceeded. In practice, the excess waste is placed in temporary underground storage, and when the capacity of this underground storage is exceeded, then the scheduled flow of ore through the system must be interrupted so that the excess waste can be removed. These intermittent interruptions of the movement of ore to the surface have the effect of intermittently underutilizing the ore-processing facilities at the surface of the mine. Hence, an additional practical advantage of using the optimization model is not only that it maximizes the mine’s capacity to move material but that it does so without intermittent interruptions caused by the stockpiles of waste.
Finally, the results illustrate the benefits of developing an operational-scale model for an underground mine. The reason operational-scale optimization models have not been widely used in the underground mining industry is because operational problems in underground mines are less generic than tactical models. That is, different types of mines have constraints or objectives that are peculiar to that mine type, and an optimization model would therefore need to be tailor-made for that type of mine in order to plan for operations. As a result, operational-scale models have not been broadly used, and heuristic approaches have been relied upon to generate solutions [6]. The results in this paper illustrate the scale of the economic benefits that can be gained by developing and using an operational scale model versus the heuristics.
6. Conclusions
In this study, a new formulation of an optimization model was developed and evaluated for solving the problem of scheduling weekly levels of operations in an underground gold mine. The results illustrate that an increase in productivity between 6% and 14.7% resulted from using the optimization model versus the currently used heuristic method. These results indicate that the development of new optimization models for underground mining problems can be a field of study with important economic consequences.
Author Contributions
Conceptualization S.E.G. and K.C.; Methodology S.E.G. and K.C.; Software S.E.G.; Validation S.E.G.; Formal Analysis S.E.G.; Investigation S.E.G.; Resources S.E.G.; Data Curation S.E.G.; Writing—original draft S.E.G.; Writing—review and editing K.C.; Visualization S.E.G.; Supervision K.C.; Project Administration K.C.; Funding acquisition K.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MITACS Accelerate Grant #457 004 3800.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yun, Q.X.; Liu, J.X.; Chen, Y.F.; Huang, G.Q. Optimization of planning and design in underground mines. In Proceedings of the 22nd International Symposium on Application of Computers and Operations Research in the Mineral Industry (APCOM-22), Berlin, Germany, 17–21 September 1990; Technical University of Berlin: Berlin, Germany, 1990; p. 255. [Google Scholar]
- Brzychczy, E. A modern tool for modelling and optimization of production in underground coal mine. In eScience on Distributed Computing Infrastructure; Springer: Cham, Switzerland, 2014; pp. 317–334. [Google Scholar]
- Newman, A.M.; Rubio, E.; Caro, R.; Weintraub, A.; Eurek, K. A review of operations research in mine planning. Interfaces 2010, 40, 222–245. [Google Scholar] [CrossRef]
- Bjørndal, T.; Herrero, I.; Newman, A.; Romero, C.; Weintraub, A. Operations research in the natural resource industry. Int. Trans. Oper. Res. 2012, 30, 39–62. [Google Scholar] [CrossRef]
- Kozan, E.; Liu, S.Q. Operations research for mining: A classification and literature review. ASOR Bull. 2011, 30, 2–23. [Google Scholar]
- Chowdu, A.; Nesbitt, P.; Brickey, A.; Newman, A.M. Operations research in underground mine planning: A review. INFORMS J. Appl. Anal. 2022, 52, 109–132. [Google Scholar] [CrossRef]
- Nehring, M.; Topal, E.; Knights, P. Dynamic short-term production scheduling and machine allocation in underground mining using mathematical programming. Min. Technol. 2010, 119, 212–220. [Google Scholar] [CrossRef]
- Martinez, M.A.; Newman, A.M. A solution approach for optimizing long-and short-term production scheduling at LKAB’s Kiruna mine. Eur. J. Oper. Res. 2011, 211, 184–197. [Google Scholar] [CrossRef]
- Howes, R.; Forrest, C. Short Interval Control in Today’s Underground Mine: A Case Study. In Proceedings of the MINExpo International 2012, Las Vegas, NV, USA, 24–26 September 2012; pp. 1–13. [Google Scholar]
- Nehring, M.; Topal, E.; Knights, P.; Kizil, M. Integrated short- and medium-term underground mine production scheduling. S. Afr. Inst. Min. Metall. J. (SAIMM) 2012, 112, 365–379. [Google Scholar]
- Little, J.; Knights, P.; Topal, E. Integrated optimization of underground mine design and scheduling. J. S. Afr. Inst. Min. Metall. 2013, 113, 775–785. [Google Scholar]
- Schulze, M.; Rieck, J.; Seifi, C.; Zimmerman, J. Machine scheduling in underground mining: An application in the potash industry. OR Spectr. 2016, 38, 365–403. [Google Scholar] [CrossRef]
- Schulze, M.; Zimmerman, J. Staff and machine shift scheduling in a German potash mine. J. Sched. 2017, 20, 635–656. [Google Scholar] [CrossRef]
- Campeau, L.P.; Gamache, M. Short-Term planning optimization model for underground mines. Comput. Oper. Res. 2019, 115, 104642. [Google Scholar] [CrossRef]
- Manríquez, F.; Pérez, J.; Morales, N. A simulation–optimization framework for short-term underground mine production scheduling. Optim. Eng. 2020, 21, 939–971. [Google Scholar] [CrossRef]
- Salkin, H.M.; De Kluyver, C.A. The knapsack problem: A survey. Nav. Res. Logist. Q. 1975, 22, 127–144. [Google Scholar] [CrossRef]
- Akçay, Y.; Li, H.; Xu, S.H. Greedy algorithm for the general multidimensional knapsack problem. Ann. Oper. Res. 2007, 150, 17–29. [Google Scholar] [CrossRef]
- Pisinger, D. An exact algorithm for large multiple knapsack problems. Eur. J. Oper. Res. 1999, 114, 528–541. [Google Scholar] [CrossRef]
- Ferdosian, N.; Othman, M.; Lun, K.Y.; Ali, B.M. Optimal solution to the fractional knapsack problem for LTE overload-state scheduling. In Proceedings of the 2016 IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Kuala Lumpur, Malaysia, 28–30 November 2016; pp. 97–102. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).