Near-Field Analysis of Turbidity Flows Generated by Polymetallic Nodule Mining Tools
Abstract
1. Introduction
- (i)
- The discharge of the sediment–water mixture from a PNMT, which remains after the separation process [6];
- (ii)
- The Deep Ocean Mining Environmental Study (DOMES) project was one of the leading projects, which aimed to obtain and investigate the necessary data for an independent impact assessment of DSM activities. DOMES was divided into two main phases as follows [19]:
- (i)
- Gaining quantitative data on the biological communities prior to mining and developing a framework to predict the impact of manganese nodule mining on the marine environment;
- (ii)
- Determining the accuracy of the environmental impact predictions obtained in the first phase through monitoring of pilot mining tests.
As a result of this project, a quantitative baseline of environmental parameters and a predictive framework were developed to characterize DSM environmental impacts. Furthermore, preliminary environmental guidelines for DSM were defined; - The Marine E-tech project took place in the Tropic Seamount in the north east Atlantic near the Canary Islands and aimed to study the environment sensitivity to Fe-Mn crust DSM operations. The Fe-Mn crusts are differentiated from polymetallic nodules as a result of different locations, depths, and DSM operation techniques. The local influencing variables (e.g., temperature, pressure) that govern the composition and formation of the Fe-Mn nodules were investigated. A Remotely Operated underwater Vehicle (ROV) was used to generate sediment plumes, and the plume dispersion was studied. The measurements showed that the plumes were significantly smaller than predicted because the effect of flocculation was not taken into account [17];
- The Towards Responsible Extraction Of Submarine Mineral Resources (TREASURE) project studied SWOE discharge from a VTS [22]. Within the scope of TREASURE, numerical simulations were performed using the drift-flux modeling approach (for details on drift-flux modeling, see [24]) to predict the VTS discharged plume characteristics (e.g., velocity and concentration) [25]. In addition, Reference [7] carried out detailed laboratory experiments to test different discharge parameters such as initial concentrations, momentum, and distance from the bed on the plume dispersion. The numerical results (e.g., velocity and concentration profiles) were compared against the experimental results, and a good agreement was found between them;
- The PLUMEX2018 field experiments were conducted in the Southern California Bight at the beginning of 2018 [26]. The Multiresolution primitive equation regional ocean modeling system (MIT-MSEAS) model was used to predict the plume dispersion, i.e., direction, velocity, and concentration. Good agreement was found between the MIT-MSEAS model and the PLUMEX field experiments [23];
- The JPI-Oceans Mining Impact II research project aimed to develop a new framework for environmental monitoring and predictions for the environmental impacts of mining operations [27]. Global Sea Mineral Resources (GSR), a subsidiary of DEME group, designed and tested a PNMT in the Clarion-Clipperton Fracture Zone (CCFZ) within the Belgian license area to assess its environmental impact [16]. GSR performed detailed measurements on the current environment (climate, geomorphological, physical oceanographic, seabed substrate characteristics, natural hazards, noise, and light). Moreover, a biological baseline was assessed based on habitat heterogeneity. The potential environmental impact was divided into six categories:
- (i)
- Habitat/nodule removal;
- (ii)
- Plume formation;
- (iii)
- Biogeochemical changes of the sediment particles;
- (iv)
- Potential release of toxic sediment into the lower water column;
- (v)
- Emissions to the air;
- (vi)
- Natural hazards (weather condition, storms).
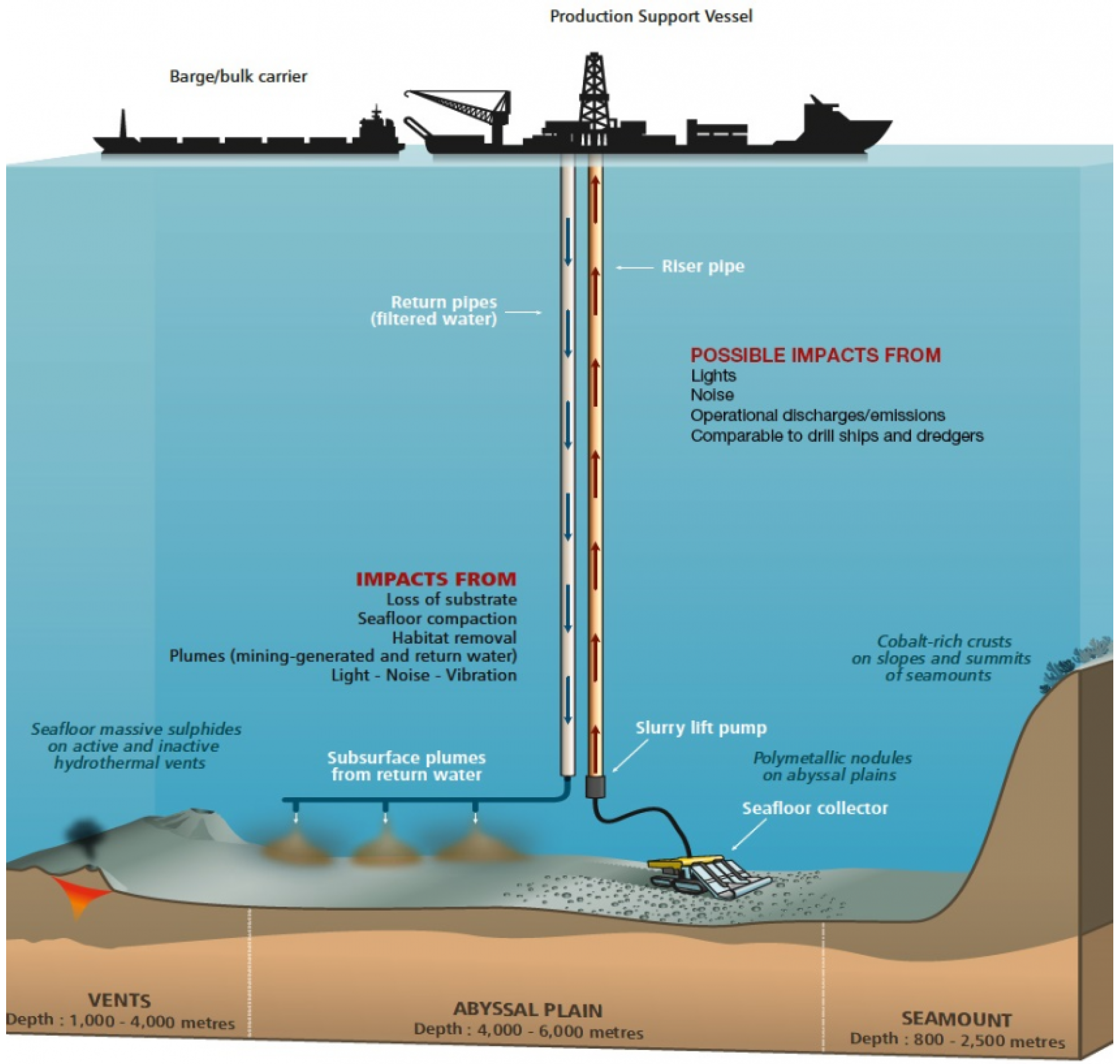
2. Discharge Process
2.1. Overview
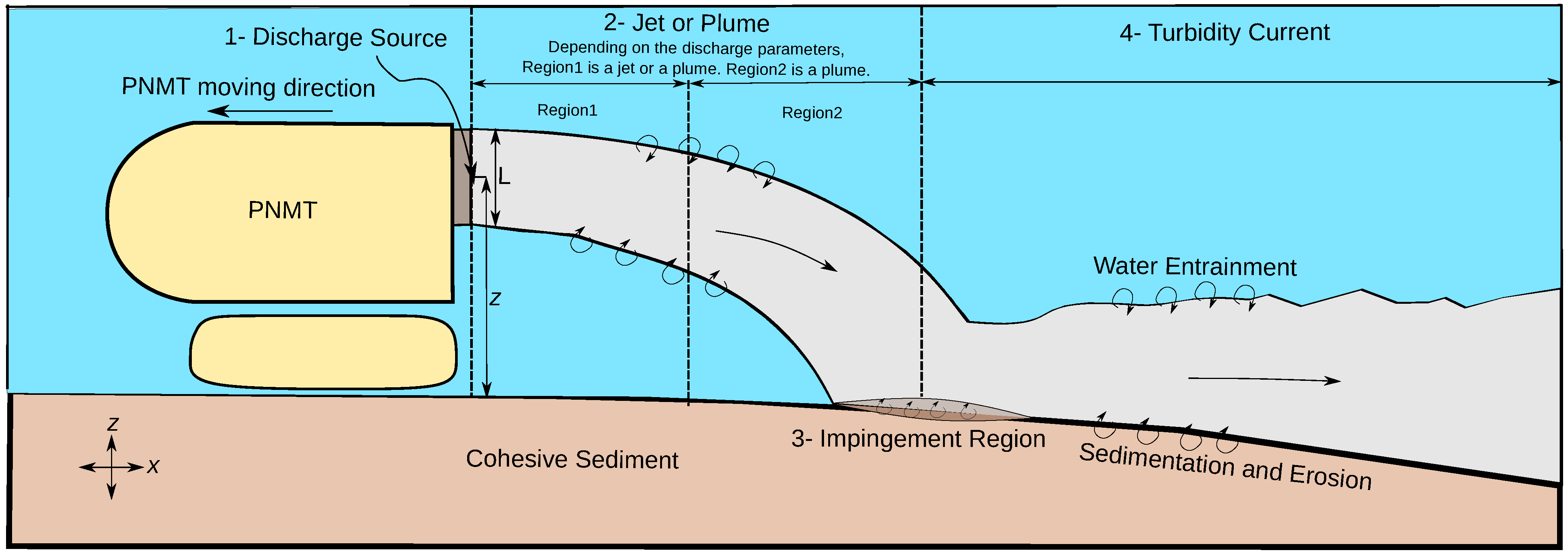
- 1.
- Discharge source: This contains the initial conditions such as the momentum, concentration of suspended sediments, and distance from the sea bed z. The physical parameters depend on the design of the PNMT (e.g., methods of collection and separation);
- 2.
- Jet or plume regime: In this region, depending on the flow discharge parameters, the flow can be a jet or plume. Later, when the buoyancy force is dominant, the flow becomes a plume (see Section 2.2 and Section 4.2);
- 3.
- Impingement region: This region is located on the sea bed. Here, the negative buoyant plume changes its direction due to the direct interaction with the seabed. Sediment deposition and possible sea bed erosion are expected to take place within this region;
- 4.
- Turbidity current: This current is formed beyond the impingement region.
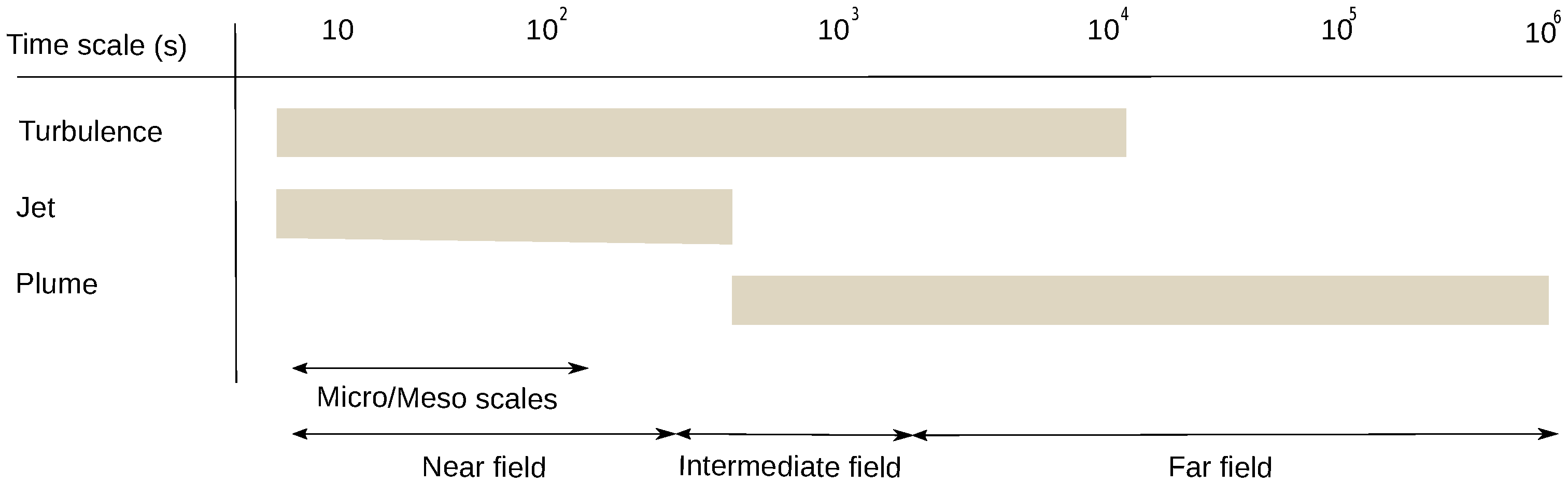
- Near-field region: This defined as the region close to the discharge apparatus, and it is mostly controlled by the discharge conditions. The flows in this region have a typical length scale up to few hundreds of meters and a time scale in the range of seconds to minutes;
- Far-field region: This is defined as the region where the plume trajectory is dominated by the environmental parameters, such as the currents and seabed topology. The flows in this region have large time and length scales, which are typically in the range of days and kilometers, respectively.
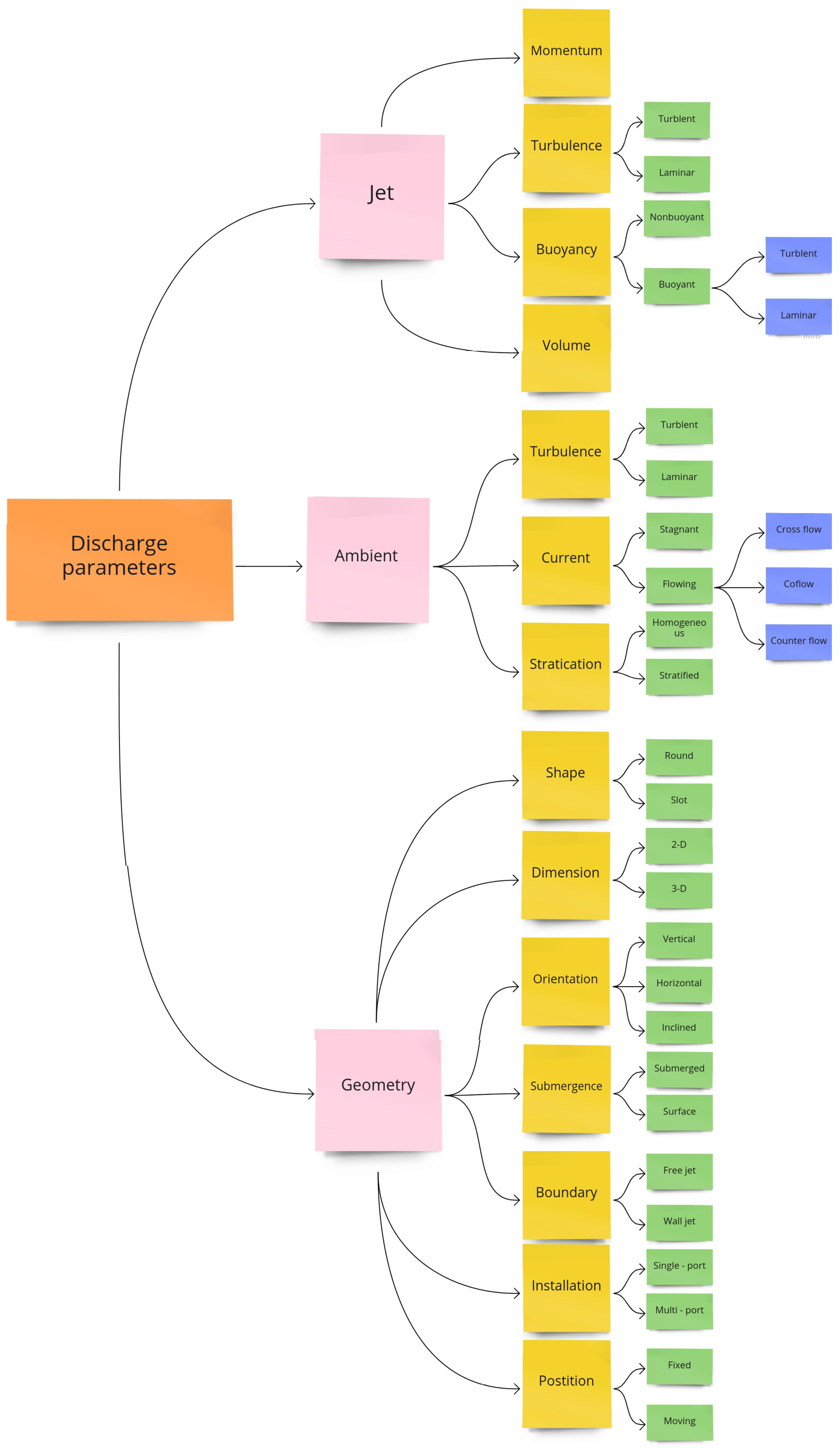
2.2. Physical Parameters
- (i)
- Mixture properties;
- (ii)
- Ambient conditions;
- (iii)
- Geometrical conditions.
3. Flow Specification
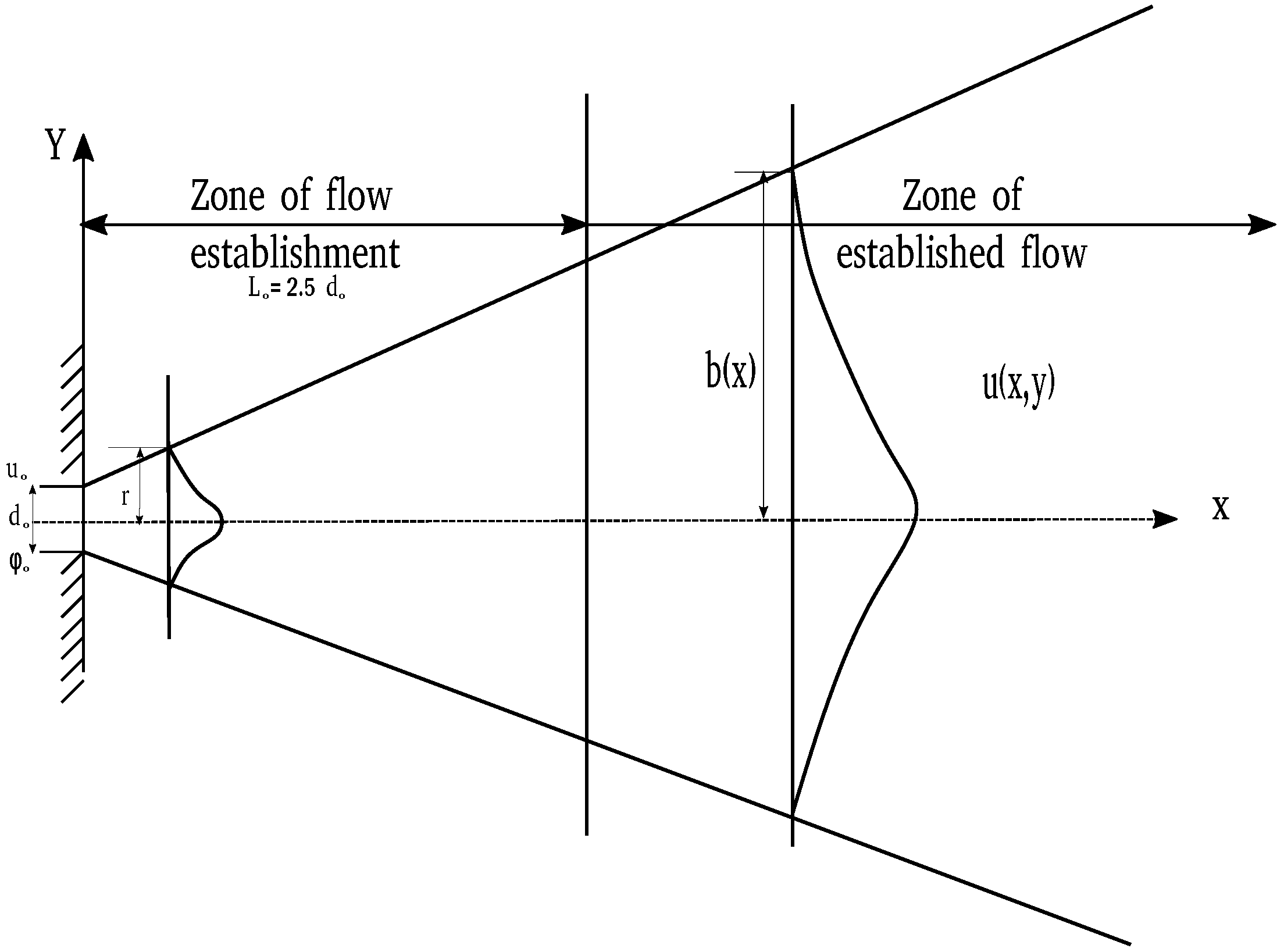
3.1. Length and Time Scales
3.2. Particle-Laden Plumes
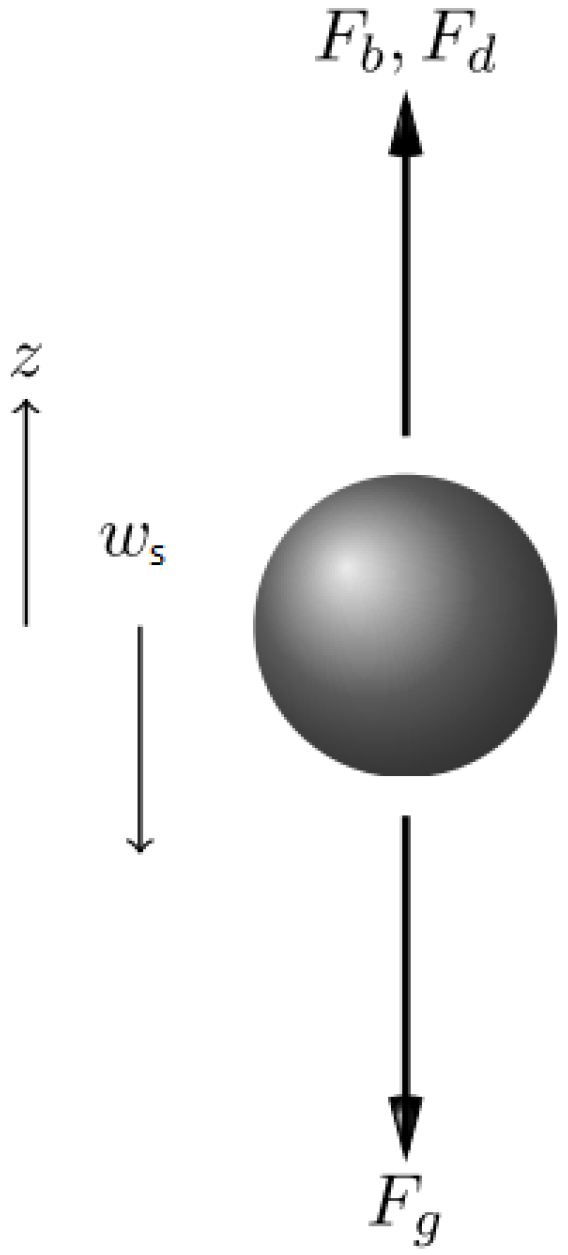
3.2.1. Particle Physics
3.2.2. Sediment-Laden Jets and Plumes
3.3. Turbidity Current
4. Flow Physics
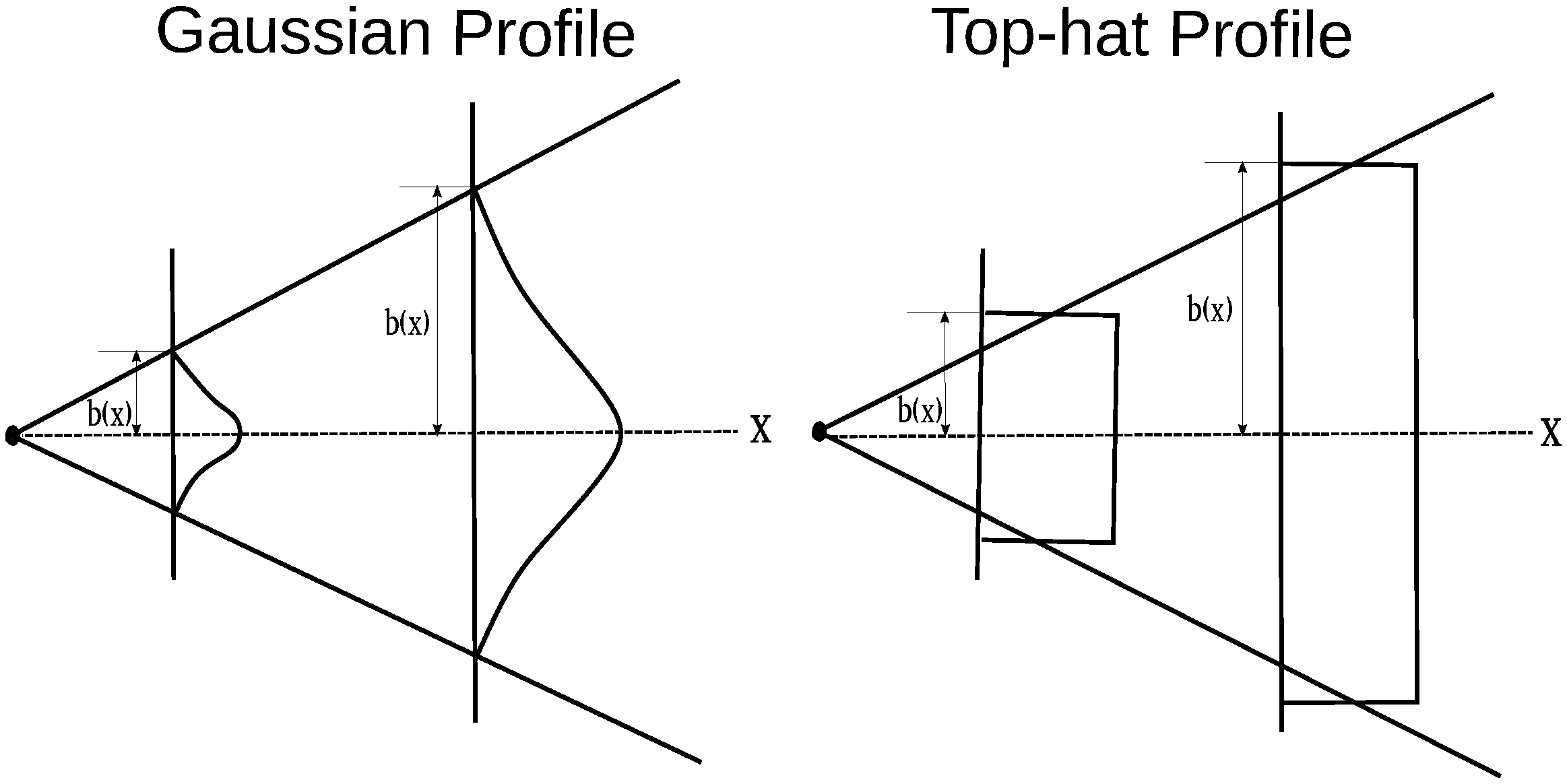
4.1. Gaussian and Top-Hat Profiles
4.2. Flux Balance Approach
- (i)
- is a pure plume.
- (ii)
- is a forced plume.
- (iii)
- is a lazy plume.
- (iv)
- is a pure jet.
4.3. Water Entrainment Theory
5. Assessment of the Near-Field Generated Plume and Turbidity Currents
5.1. Lagrangian Plume Model
5.2. Four-Equation Model for Turbidity Currents
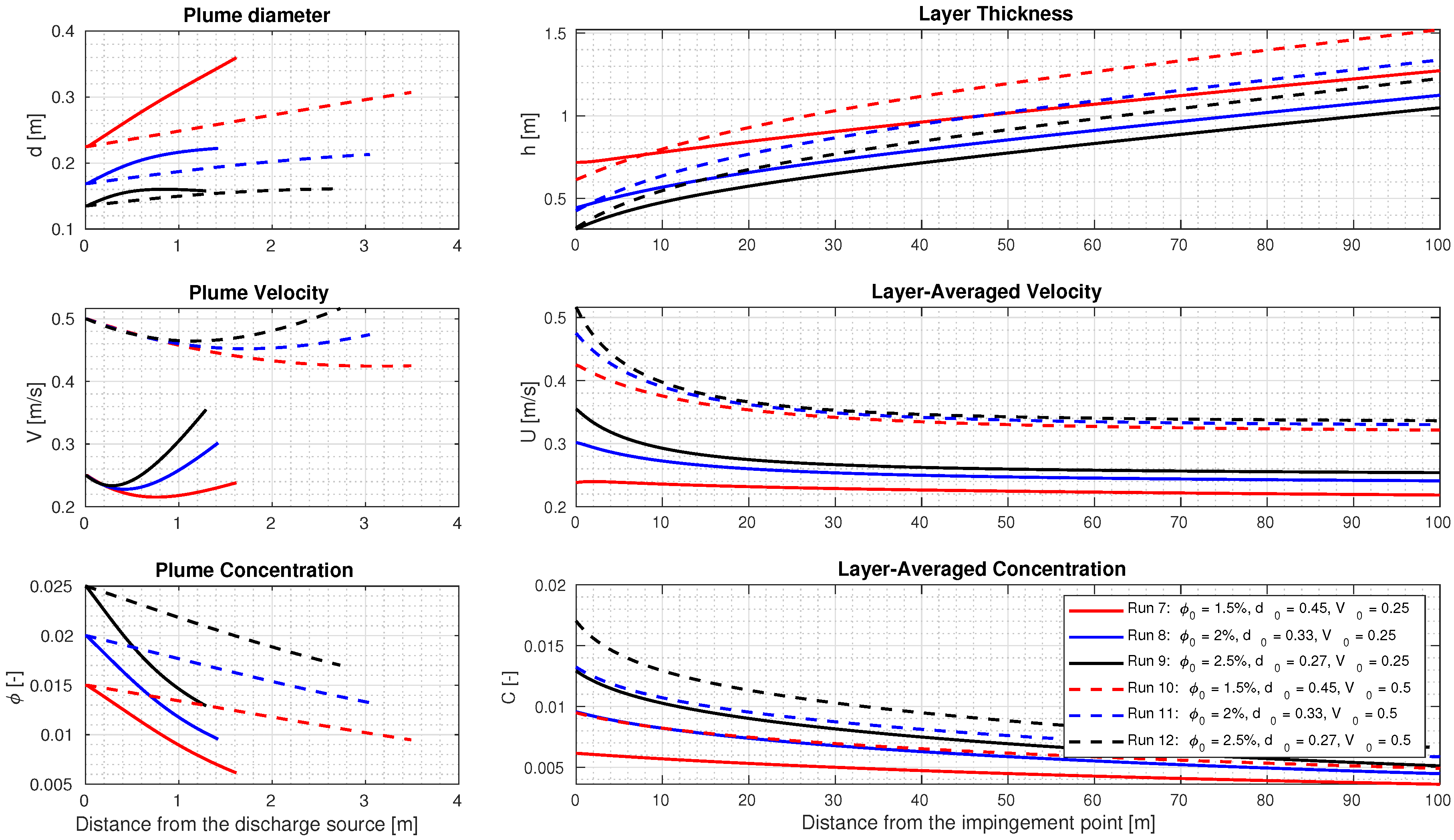
5.3. Model Application
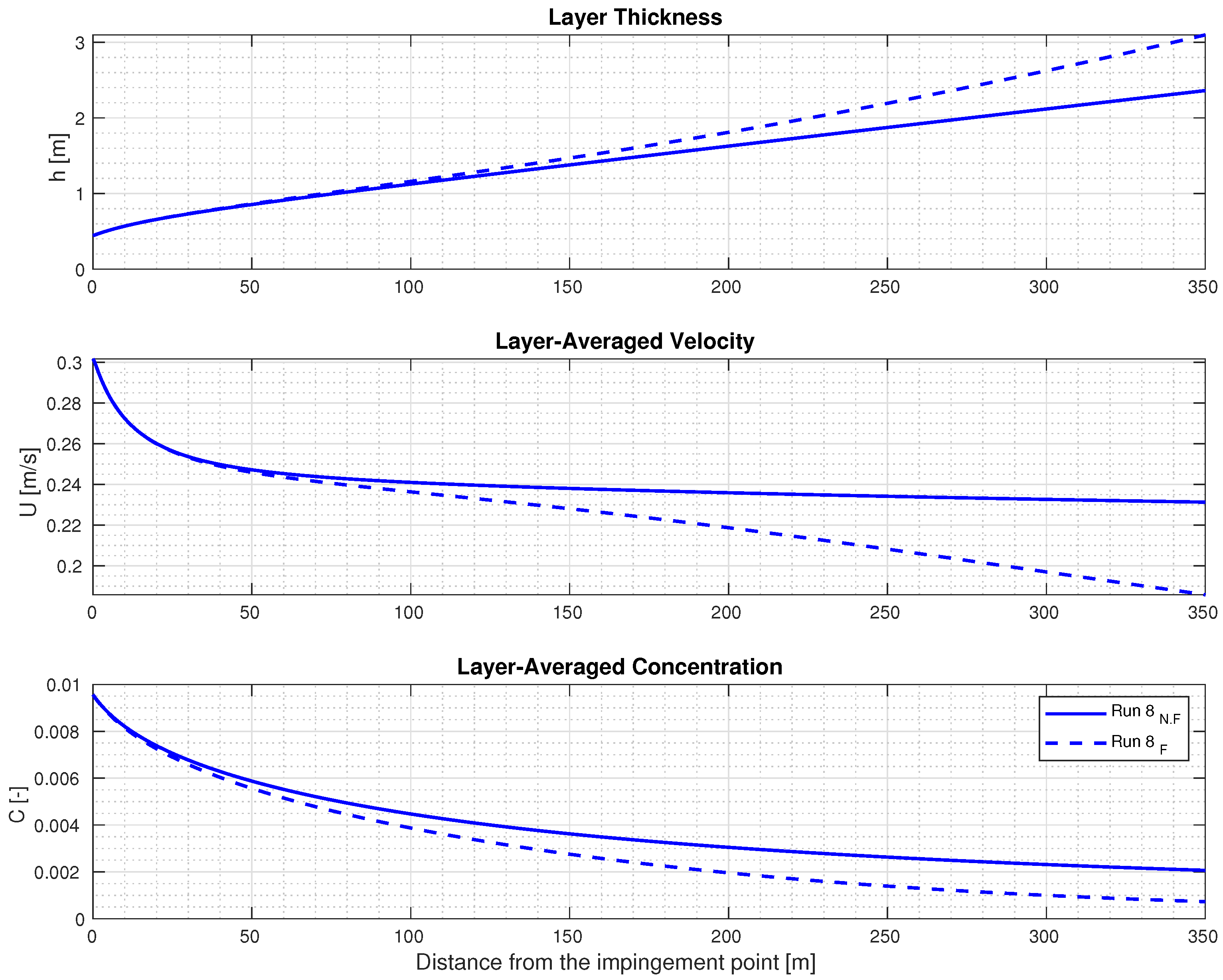
5.4. Comparison of the Results
6. Flocculation
6.1. Background
- (i)
- Brownian motion, i.e., the random movement of the particles;
- (ii)
- Differential settling, i.e., the particles with high settling velocities collide with the particles with low settling velocities and aggregate together;
- (iii)
- Turbulent mixing.
6.2. Numerical Assessment of the Flocculation Effect
7. Synthesis and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Wu, R.; Geng, Y.; Liu, W. Trends of natural resource footprints in the BRIC (Brazil, Russia, India and China) countries. J. Clean. Prod. 2017, 142, 775–782. [Google Scholar] [CrossRef]
- Hein, J.R.; Koschinsky, A.; Kuhn, T. Deep-ocean polymetallic nodules as a resource for critical materials. Nat. Rev. Earth Environ. 2020, 1, 158–169. [Google Scholar] [CrossRef]
- Toro, N.; Robles, P.; Jeldres, R.I. Seabed mineral resources, an alternative for the future of renewable energy: A critical review. Ore Geol. Rev. 2020, 126, 103699. [Google Scholar] [CrossRef]
- Pak, S.J.; Seo, I.; Lee, K.Y.; Hyeong, K. Rare earth elements and other critical metals in deep seabed mineral deposits: Composition and implications for resource potential. Minerals 2019, 9, 3. [Google Scholar] [CrossRef]
- Schriever, G.; Thiel, H. Tailings and Their Disposal in Deep-Sea Mining. In Proceedings of the Tenth ISOPE Ocean Mining and Gas Hydrates Symposium, Szczecin, Poland, 22–26 September 2013. [Google Scholar]
- Decrop, B.; Wachter, T.D. Detailed CFD Simulations For near Field Dispersion of Deep Sea Mining Plumes. In Proceedings of the World dredging conference Wodcon xxll, Shanghai, China, 22–26 April 2019; pp. 116–127. [Google Scholar]
- Grunsven, F.; Keetels, G.; Rhee, C. The Initial Spreading of Turbidity Plumes—Dedicated Laboratory Experiments for Model Validation. In Proceedings of the 47th Underwater Mining Conference, Bergen, Norway, 10–14 September 2018. [Google Scholar]
- Rzeznik, A.J.; Flierl, G.R.; Peacock, T. Model investigations of discharge plumes generated by deep-sea nodule mining operations. Ocean Eng. 2019, 172, 684–696. [Google Scholar] [CrossRef]
- Corliss, B.H. Microhabitats of benthic foraminifera within deep-sea sediments. Nature 1985, 314, 4–7. [Google Scholar] [CrossRef]
- Thiel, H. Anthropogenic impacts on the deep sea. In Ecosystems of the Deep Oceans; Elsevier: New York, NY, USA, 2003; pp. 427–471. [Google Scholar] [CrossRef]
- Sharma, R. Environmental issues of deep-sea mining. Procedia Earth Planet. Sci. 2015, 11, 204–211. [Google Scholar] [CrossRef]
- Cuyvers, L.; Berry, W.; Kristina, G.; Torsten, T.; Caroline, W. Deep Seabed Mining: A Rising Environmental Challenge; IUCN and Gallifrey Foundation: Gland, Switzerland, 2018. [Google Scholar]
- Sharma, R.; Nagender Nath, B.; Parthiban, G.; Jai Sankar, S. Sediment redistribution during simulated benthic disturbance and its implications on deep seabed mining. Deep.-Sea Res. Part Ii Top. Stud. Oceanogr. 2001, 48, 3363–3380. [Google Scholar] [CrossRef]
- Decrop, B.; Mulder, T.O.M.D.E.; Troch, P.; Toorman, E.; Sas, M. Experimental investigation of negatively buoyant sediment plumes resulting from dredging operations. In Proceedings of the 4th International Conference on the Application of Physical Modelling to Port and Coastal Protection, Gent, Belgium, 17–20 September 2012; pp. 573–582. [Google Scholar]
- de Wit, L.; van Rhee, C.; Keetels, G. Turbulent interaction of a buoyant jet with cross-flow. J. Hydraul. Eng. 2014, 140, 1–14. [Google Scholar] [CrossRef]
- BGR. Environmental Impact Assessment; Technical Report; Global Sea Mineral Resources, GSR, Member of Deme Group: Zwijndrecht, Belgium, 2019. [Google Scholar]
- Spearman, J.; Taylor, J.; Crossouard, N.; Cooper, A.; Turnbull, M.; Manning, A.; Lee, M.; Murton, B. Measurement and modeling of deep sea sediment plumes and implications for deep sea mining. Sci. Rep. 2020, 10, 5075. [Google Scholar] [CrossRef]
- Gillard, B.; Purkiani, K.; Chatzievangelou, D.; Vink, A.; Iversen, M.H.; Thomsen, L. Physical and hydrodynamic properties of deep sea mining-generated, abyssal sediment plumes in the Clarion Clipperton Fracture Zone (eastern-central Pacific). Elementa 2019, 7, 5. [Google Scholar] [CrossRef]
- Department of Commerce. Deep Ocean Mining Enviromental Study-Information and Issues; Technical Report; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1977.
- Thiel, H.; Schriever, G.; Borowski, C.; Bussau, C.; Hansen, D.; Melles, J.; Post, J.; Steinkamp, K.; Watson, K. Cruise-Report DISCOL 1, SONNE—Cruise 61. In Balboa/Panama—Calloa/Peru; Institut für Hydrobiologie und Fischereiwissenschaft, Universität Hamburg: Hamburg, German, 1989. [Google Scholar]
- Oebius, H.U.; Becker, H.J.; Rolinski, S.; Jankowski, J.A. Parametrization and evaluation of marine environmental impacts produced by deep-sea manganese nodule mining. Deep.-Sea Res. Part Ii Top. Stud. Oceanogr. 2001, 48, 3453–3467. [Google Scholar] [CrossRef]
- Reichart, G.J.; Duineveld, G.; van Rhee, C.; Lindeboom, H.J. Towards Responsible Extraction of Submarine Mineral Resources (TREASURE); Technical Report; STW: Utrecht, The Netherlands, 2013. [Google Scholar]
- Muñoz-Royo, C.; Peacock, T.; Alford, M.H.; Smith, J.A.; Le Boyer, A.; Kulkarni, C.S.; Lermusiaux, P.F.; Haley, P.J.; Mirabito, C.; Wang, D.; et al. Extent of impact of deep-sea nodule mining midwater plumes is influenced by sediment loading, turbulence and thresholds. Commun. Earth Environ. 2021, 2, 148. [Google Scholar] [CrossRef]
- Goeree, J.C. Drift-Flux Modeling of Hyper-Concentrated Solid-Liquid Flows in Dredging Applications. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Grunsven, F.; Keetels, G.; van Rhee, C. Modeling offshore mining turbidity sources. In Proceedings of the WODCON XXI, Miami, FL, USA, 13–17 June 2016. [Google Scholar]
- Kulkarni, C.S.; Haley, P.J.; Lermusiaux, P.F.; Dutt, A.; Gupta, A.; Mirabito, C.; Subramani, D.N.; Jana, S.; Ali, W.H.; Peacock, T.; et al. Real-Time Sediment Plume Modeling in the Southern California Bight. In Proceedings of the OCEANS 2018 MTS/IEEE, Charleston, SC, USA, 22–25 October 2018; JPI Oceans: Bruxelles, Belgium, 2018; pp. 1–10. [Google Scholar]
- Haeckel, M. Mining Impact; Environmental Impacts and Risks of Deep-Sea Mining; 2018; pp. 1–64. Available online: https://www.science.org/doi/10.1126/science.aap7301 (accessed on 20 October 2021).
- Lee, W.Y.; Li, A.C.; Lee, J.H. Structure of a horizontal sediment-laden momentum jet. J. Hydraul. Eng. 2013, 139, 124–140. [Google Scholar] [CrossRef]
- Parker, G.; Pantin, H.M.; Fukushima, Y. Self-Accelerating Turbidity Currents. J. Fluid Mech. 1986, 171, 145–181. [Google Scholar] [CrossRef]
- Verichev, S.N.; Rhee, C.V.; Jak, R.G.; Vries, P.D. Towards Zero Impact of Deep Sea Offshore Projects towards Zero Impact of Deep Sea Offshore Projects an Assessment Framework for Future Environmental Studies of Deep-Sea; The Ministry of Economic Affairs, Agriculture and Innovation: Den Haag, The Netherlands, 2014. [Google Scholar]
- Pfafflin, J.R. Environmental Impact Statement; Technical Report 1; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Lescinski, J.; Jeuken, C.; Cronin, K.; Vroom, J.; Elias, E. Modeling Investigations on Mine Tailing Plume Dispersion on the Chatham Rise1209110; Technical Report. 2014. Available online: https://www.epa.govt.nz/assets/FileAPI/proposal/EEZ000006/Applicants-proposal-documents/589e6cb893/EEZ000006-Appendix25-Deltares-2014b-Modelling-investigations.pdf (accessed on 29 October 2021).
- Fernando, H.J. Handbook of Environmental Fluid Dynamics; Volume One: Overview and Fundamentals; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Chen, H.B. Turbulent Boyant Jets and Plumes in Flowing Ambient Environments. Ph.D. Thesis, Aalborg University, Aalborg Øst, Denmark, 1991. [Google Scholar] [CrossRef]
- De Wit, L. Near Field 3D CFD Modeling of Overflow Plumes. In Proceedings of the 19th World Dredging Congress, Beijing, China, 9–14 September 2010. [Google Scholar]
- Lee, J.H.-w.; Chu, V.; Chu, V.H. Turbulent Jets and Plumes: A Lagrangian Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003; Volume 1. [Google Scholar]
- Fischer, H.B.; List, J.E.; Koh, C.R.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press: Cambridge, MA, USA, 1979. [Google Scholar]
- Prosperetti, A.; Tryggvason, G. Computational Methods for Multiphase Flow; Cambridge University Press: Columbia, MD, USA, 2009. [Google Scholar]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops and Particles; Dover Publications: New York, NY, USA, 1979; Volume 94, pp. 795–796. [Google Scholar] [CrossRef]
- Ferguson, R.; Church, M. A Simple Universal Equation for Grain Settling Velocity. J. Sediment. Res. 2004, 74, 933–937. [Google Scholar] [CrossRef]
- Richardson, J.F.; Zaki, W. Sedimentation and Fluidisation. Part 1. Trans. Inst. Chem. Eng 1954, 32, 35–53. [Google Scholar] [CrossRef]
- GSR. Blue Nodules Deliverable report D3.4, Report Describing the Process Flow Overview; Technical Report. 2018; Available online: https://blue-nodules.eu/downloads (accessed on 29 October 2021).
- Zawadzki, D.; Maciąg, Ł.; Abramowski, T.; McCartney, K. Fractionation trends and variability of rare earth elements and selected critical metals in pelagic sediment from abyssal basin of NE Pacific (Clarion-Clipperton Fracture Zone). Minerals 2020, 10, 320. [Google Scholar] [CrossRef]
- Maciag, L.; Harff, J. Application of multivariate geostatistics for local-scale lithological mapping—Case study of pelagic surface sediments from the Clarion-Clipperton Fracture Zone, north-eastern equatorial Pacific (Interoceanmetal claim area). Comput. Geosci. 2020, 139, 104474. [Google Scholar] [CrossRef]
- Bischoff, J.L.; Heath, G.R.; Leinen, M. Geochemistry of deep-sea sediments from the Pacific manganese nodule province: DOMES Sites A, B, and C. In Marine Geology and Oceanography of the Pacific Manganese Nodule Province; Springer: Berlin/Heidelberg, Germany, 1979; pp. 397–436. [Google Scholar]
- Bleninger, T.; Lipari, G.; Jirka, G.H. Design and optimization program for internal diffuser hydraulics. In Proceedings of the 2nd International Conference Marine Waste Water Discharges, Istanbul, Turkey, 9 January 2002. [Google Scholar]
- Neves, M.; Neves, A.; Bleninger, T. Prediction on particle deposition in effluent disposal system. In Proceedings of the 2nd Intenational Conference Marine Waste Water Discharges, International Association for Hydro-Environment Engineering and Research (IAHR) and International Water Association (IWA), Istanbul, Turkey, 16–20 September 2002. [Google Scholar]
- Lane-Serff, G.F.; Moran, T.J. Sedimentation from buoyant jets. J. Hydraul. Eng. 2005, 131, 166–174. [Google Scholar] [CrossRef]
- Terfous, A.; Chiban, S.; Ghenaim, A.; Terfous, A.; Chiban, S.; Ghenaim, A. Modeling sediment deposition from marine outfall jets. Taylor Fr. J. Environ. Technol. 2019, 37, 1865–1874. [Google Scholar] [CrossRef] [PubMed]
- Cuthbertson, A.J.; Apsley, D.D.; Davies, P.A.; Lipari, G.; Stansby, P.K. Deposition from particle-laden, plane, turbulent, buoyant jets. J. Hydraul. Eng. 2008, 134, 1110–1122. [Google Scholar] [CrossRef]
- Hage, S.; Cartigny, M.J.; Sumner, E.J.; Clare, M.A.; Hughes Clarke, J.E.; Talling, P.J.; Lintern, D.G.; Simmons, S.M.; Silva Jacinto, R.; Vellinga, A.J.; et al. Direct monitoring reveals initiation of turbidity currents from extremely dilute river plumes. Geophys. Res. Lett. 2019, 46, 11310–11320. [Google Scholar] [CrossRef]
- Parsons, J.D.; Friedrichs, C.T.; Traykovski, P.A.; Mohrig, D.; Imran, J.; Syvitski, J.P.M.; Parker, G.; Puig, P.; Buttles, J.L.; Garca, M.H. The Mechanics of Marine Sediment Gravity Flows. In Continental Margin Sedimentation; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 37, pp. 275–334. [Google Scholar] [CrossRef]
- Kneller, B.; Buckee, C. The structure and fluid mechanics of turbidity currents: A review of some recent studies and their geological implications. Sedimentology 2000, 47, 62–94. [Google Scholar] [CrossRef]
- Normandeau, A.; Lajeunesse, P.; St-Onge, G.; Bourgault, D.; Drouin, S.S.O.; Senneville, S.; Bélanger, S. Morphodynamics in sediment-starved inner-shelf submarine canyons (Lower St. Lawrence Estuary, Eastern Canada). Mar. Geol. 2014, 357, 243–255. [Google Scholar] [CrossRef]
- Parsons, J.D.; Bush, J.W.; Syvitski, J.P. Hyperpycnal plume formation from riverine outflows with small sediment concentrations. Sedimentology 2001, 48, 465–478. [Google Scholar] [CrossRef]
- Alhaddad, S.; Labeur, R.J.; Uijttewaal, W. Large-Scale Experiments on Breaching Flow Slides and the Associated Turbidity Current. J. Geophys. Res. Earth Surf. 2020, 125, e2020JF005582. [Google Scholar] [CrossRef]
- Middleton, G.V. Sediment deposition from turbidity currents. Annu. Rev. Earth Planet. Sci. 1993, 21, 89–114. [Google Scholar] [CrossRef]
- Keulegan, G.H. Twelfth Progress Report on Model Laws for Density Currents: The Motion of Saline Fronts in Still Water; US Department of Commerce, National Bureau of Standards: Gaithersburg, MD, USA, 1958.
- Allen, J. Mixing at turbidity current heads, and its geological implications. J. Sediment. Res. 1971, 41, 97–113. [Google Scholar]
- Allen, J. Principles of Physical Sedimentology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Simpson, J.E.; Britter, R.E. Experiments on the Dynamics of the Front of a Gravity Current. J. Fluid Mech. 1980, 88, 223–240. [Google Scholar]
- Parker, G.; Garcia, M.; Fukushima, Y.; Yu, W. Experiments on turbidity currents over an erodible bed. J. Hydraul. Res. 1987, 25, 123–147. [Google Scholar] [CrossRef]
- Kirwan, A.D.; Doyle, L.J.; Bowles, W.D.; Brooks, G.R. Time-dependent hydrodynamic models of turbidity currents analyzed with data from the Grand Banks and Orleansville events. J. Sediment. Res. 1986, 56, 379–386. [Google Scholar] [CrossRef]
- Johnson, M.A. Application of theory to an Atlantic turbidity-current paths. Sedimentology 1966, 7, 117–129. [Google Scholar] [CrossRef]
- Zedler, E.A.; Street, R.L. Large-eddy simulation of sediment transport: Currents over ripples. J. Hydraul. Eng. 2001, 127, 444–452. [Google Scholar] [CrossRef]
- Ooi, S.K.; Constantinescu, G.; Weber, L.J. 2D large-eddy simulation of lock-exchange gravity current flows at high Grashof numbers. J. Hydraul. Eng. 2007, 133, 1037–1047. [Google Scholar] [CrossRef]
- Henniger, R.; Kleiser, L. Large-eddy simulation of particle-driven gravity currents using the Relaxation-Term model. J. Phys. Conf. Ser. 2011, 318, 052008. [Google Scholar] [CrossRef]
- Alhaddad, S.; de Wit, L.; Labeur, R.J.; Uijttewaal, W. Modeling of Breaching-Generated Turbidity Currents Using Large Eddy Simulation. J. Mar. Sci. Eng. 2020, 8, 728. [Google Scholar] [CrossRef]
- Morton, B.R.; Turner, G.T.; Turner, J.S. Turbulent Gravitational Convection from Maintained and Instantaneous. Ser. A Math. Phys. Publ. R. 1956, 234, 1–23. [Google Scholar]
- Morton, B.R. Forced plumes. J. Fluid Mech. 1959, 5, 151–163. [Google Scholar] [CrossRef]
- Turner, J. The ‘starting plume’ in neutral surroundings. J. Fluid Mech. 1962, 13, 356–368. [Google Scholar] [CrossRef]
- Middleton, G.V. Experiments on density and turbidity currents: I. Motion of the head. Can. J. Earth Sci. 1966, 3, 523–546. [Google Scholar] [CrossRef]
- Delichatsios, M.A. Time similarity analysis of unsteady buoyant plumes in neutral surroundings. J. Fluid Mech. 1979, 93, 241–250. [Google Scholar] [CrossRef]
- Yu, H.Z. Transient plume influence in measurement of convective heat release bates of fast-growing fires using a large-scale fire products collector. J. Heat Transf. 1990, 112, 186–191. [Google Scholar] [CrossRef]
- Davidson, G.A. Gaussian versus top-hat profile assumptions in integral plume models. Atmos. Environ. 1986, 20, 471–478. [Google Scholar] [CrossRef]
- Hanna, S.R.; Briggs, G.A.; Hosker, R.P. Atmospheric Turbulence and Diffusion Laboratory National Oceanic and Atmospheric Administration; Journal of Air Pollution Modeling and Its Application I; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1982; Volume 1. [Google Scholar]
- McKernan, J.L.; Ellenbecker, M.J.; Holcroft, C.A.; Petersen, M.R. Evaluation of a proposed area equation for improved exothermic process control. Ann. Occup. Hyg. 2007, 51, 725–738. [Google Scholar] [CrossRef][Green Version]
- Hunt, G.R.; Van Den Bremer, T.S. Classical plume theory: 1937-2010 and beyond. IMA J. Appl. Math. 2011, 76, 424–448. [Google Scholar] [CrossRef]
- Marjanovic, G.; Taub, G.; Balachandar, S. On the effects of buoyancy on higher order moments in lazy plumes. J. Turbul. 2019, 20, 121–146. [Google Scholar] [CrossRef]
- Morton, B.; Middleton, J. Scale diagrams for forced plumes. J. Fluid Mech. 1973, 58, 165–176. [Google Scholar] [CrossRef]
- Carlotti, P.; Hunt, G.R. Analytical solutions for turbulent non-Boussinesq plumes. J. Fluid Mech. 2005, 538, 343–359. [Google Scholar] [CrossRef]
- Turner, J.S. Turbulent entrainment: The development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 1986, 173, 431–471. [Google Scholar] [CrossRef]
- Rooney, G.G.; Linden, P.F. Similarity considerations for non-Boussinesq plumes in an unstratified environment. J. Fluid Mech. 1996, 318, 237–250. [Google Scholar] [CrossRef]
- Carazzo, G.; Kaminski, E.; Tait, S. The route to self-similarity in turbulent jets and plumes. J. Fluid Mech. 2006, 547, 137–148. [Google Scholar] [CrossRef]
- Van Reeuwijk, M.; Craske, J. Energy-consistent entrainment relations for jets and plumes. J. Fluid Mech. 2015, 782, 333–355. [Google Scholar] [CrossRef]
- Priestley, C.H.; Ball, F.K. Continuous convection from an isolated source of heat. Q. J. R. Meteorol. Soc. 1955, 81, 144–157. [Google Scholar] [CrossRef]
- Telford, J.W. The Convective Mechanism in Clear Air. J. Atmos. Sci. 1966, 23, 652–666. [Google Scholar] [CrossRef]
- Fox, D.G. Forced plume in a stratified fluid. J. Geophys. Res. 1970, 75, 6818–6835. [Google Scholar] [CrossRef]
- van Reeuwijk, M.; Salizzoni, P.; Hunt, G.R.; Craske, J. Turbulent transport and entrainment in jets and plumes: A DNS study. Phys. Rev. Fluids 2016, 1, 074301. [Google Scholar] [CrossRef]
- Van den Bremer, T.; Hunt, G.R. Universal solutions for Boussinesq and non-Boussinesq plumes. J. Fluid Mech. 2010, 644, 165–192. [Google Scholar] [CrossRef]
- Craske, J.; Debugne, A.L.; Van Reeuwijk, M. Shear-flow dispersion in turbulent jets. J. Fluid Mech. 2015, 781, 28–51. [Google Scholar] [CrossRef][Green Version]
- Lee, J.H.; Cheung, V. Generalized Lagrangian Model For Buoyant Jets in Current. J. Environ. Eng. 1991, 116, 1085–1106. [Google Scholar] [CrossRef]
- Alhaddad, S.; Labeur, R.J.; Uijttewaal, W. Breaching flow slides and the associated turbidity current. J. Mar. Sci. Eng. 2020, 8, 67. [Google Scholar] [CrossRef]
- Winterwerp, J.C.; van Kesteren, W.G.; van Prooijen, B.; Jacobs, W. A conceptual framework for shear flow–induced erosion of soft cohesive sediment beds. J. Geophys. Res. Ocean. 2012, 117, 1–17. [Google Scholar] [CrossRef]
- Winterwerp, J.C.; van Kesteren, W.G. Introduction to the Physics of Cohesive Sediment in the Marine Environment; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Smith, S.J.; Friedrichs, C.T. Size and settling velocities of cohesive flocs and suspended sediment aggregates in a trailing suction hopper dredge plume. Cont. Shelf Res. 2011, 31, S50–S63. [Google Scholar] [CrossRef]



| Application | Solid Flux Per Unit Width | Concentration Range | D10 | D50 | D90 |
|---|---|---|---|---|---|
| Seafloor Massive Sulfides (SMSs) [30] | 163 kg/s | 250 g/L | 19 μm | 40 μm | 70 μm |
| Nodules [6] | 65.9–212.3 kg/s | 10–170 g/L | - | 10 μm | - |
| Nodules [31] | 65.9–212.3 kg/s | 10–170 g/L | 2 μm | 15 μm | 70 μm |
| Fe-Mn crusts [17] | 0.2 kg/s | 20–100 mg/L | - | - | - |
| Phosphorite [32] | 827 kg/s | 449 g/L | 10 μm | 80 μm | 300 μm |
| Name of Sediment Fraction | Diameter Limits (Micro) WRB Classification | GSR Data Average (%) | NTNU Data BC062 (%) | NTNU Data BC064 (%) | IOM Data Average (%) |
|---|---|---|---|---|---|
| Clay | <2 | 12 | 11.3 | 14.5 | 23.24 |
| Silt | 2–63 | 76.2 | 85.7 | 82.5 | 70.36 |
| Sand | 63–2000 | 11.8 | 3 | 3 | 6.13 |
| IOM 1 | IOM 2 | IOM 3 | Site A | Site B | Site C | GSR | IOM | |
|---|---|---|---|---|---|---|---|---|
| Smectite (%) | 12.71 | 17.33 | 16.49 | 52 | 38 | 40 | 36.41 | 16.3 |
| Illite (%) | 13.82 | 12.05 | 14.25 | 31 | 42 | 50 | 48.34 | 13.2 |
| Kaolinite (%) | 0.65 | 0.43 | 0.54 | 10.33 | 1 | |||
| Chlorite (%) | 1.7 | 1.85 | 2.35 | 4.92 | 1.5 | |||
| Amorphic (%) | 50.47 | 47.09 | 44.42 |
| Source | Flow | Fluid | Nozzle | Method | Re | ||
|---|---|---|---|---|---|---|---|
| Forstall Gaylord (1955) | J | L | P | w | - | 10–20 | 0.070 |
| Wang Law (2002) | J | L | P | l | 12,700 | 40–80 | 0.075 |
| Papanicolaou List (1988) | J | L | c | l | 2460–10,900 | 40–50 | 0.074 |
| Papanicolaou List (1988) | J | L | c | l | 2460–10,900 | 50–80 | 0.079 |
| Papanicolaou List (1988) | P | L | c | l | 600 | 22–40 | 0.130 |
| Papanicolaou List (1988) | P | L | c | l | 600 | 41–53 | 0.126 |
| Papanicolaou List (1988) | P | L | c | l | 600 | 56–85 | 0.121 |
| Wang Law (2002) | P | L | c | l | 1550–12,700 | 31–55 | 0.124 |
| D50 | ρp | PI | γcr | n | cv | cu |
|---|---|---|---|---|---|---|
| 0.012 mm | 1350 | 70% | 0.7 | 0.67 | m/s | 0.2 kPa |
| Runs | Initial Condition | Plume Model | Turbidity Current Model | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0.015 | 0.45 | 0.25 | 1.69 | - | - | - | - | 1.69 | 0.274 | 0.0067 | 0.91 | 1.672 |
| 2 | 0.02 | 0.34 | 0.25 | 1.69 | - | - | - | - | 1.69 | 0.274 | 0.0075 | 0.81 | 1.669 | |
| 3 | 0.025 | 0.27 | 0.25 | 1.69 | - | - | - | - | 1.69 | 0.274 | 0.0081 | 0.75 | 1.670 | |
| 4 | 0.5 | 0.015 | 0.45 | 0.25 | 1.69 | 0.97 | 0.009 | 0.62 | 0.22 | 1.22 | 0.235 | 0.0051 | 1.00 | 1.206 |
| 5 | 0.02 | 0.34 | 0.25 | 1.69 | 0.86 | 0.013 | 0.43 | 0.25 | 1.33 | 0.235 | 0.0051 | 1.00 | 1.206 | |
| 6 | 0.025 | 0.27 | 0.25 | 1.69 | 0.76 | 0.017 | 0.32 | 0.27 | 1.42 | 0.274 | 0.0059 | 0.91 | 1.322 | |
| 7 | 1.5 | 0.015 | 0.45 | 0.25 | 1.69 | 1.62 | 0.006 | 0.72 | 0.24 | 1.05 | 0.254 | 0.0065 | 0.85 | 1.398 |
| 8 | 0.02 | 0.34 | 0.25 | 1.69 | 1.42 | 0.010 | 0.44 | 0.30 | 1.27 | 0.220 | 0.0038 | 1.26 | 1.050 | |
| 9 | 0.025 | 0.27 | 0.25 | 1.69 | 1.29 | 0.013 | 0.32 | 0.35 | 1.44 | 0.244 | 0.0047 | 1.11 | 1.269 | |
| 10 | 0.015 | 0.45 | 0.5 | 1.69 | 3.48 | 0.010 | 0.61 | 0.43 | 2.48 | 0.257 | 0.0054 | 1.03 | 1.434 | |
| 11 | 0.02 | 0.34 | 0.5 | 1.69 | 3.05 | 0.013 | 0.43 | 0.47 | 2.67 | 0.323 | 0.0060 | 1.31 | 2.440 | |
| 12 | 0.025 | 0.27 | 0.5 | 1.69 | 2.73 | 0.017 | 0.32 | 0.52 | 2.83 | 0.332 | 0.0060 | 1.31 | 2.605 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elerian, M.; Alhaddad, S.; Helmons, R.; van Rhee, C. Near-Field Analysis of Turbidity Flows Generated by Polymetallic Nodule Mining Tools. Mining 2021, 1, 251-278. https://doi.org/10.3390/mining1030017
Elerian M, Alhaddad S, Helmons R, van Rhee C. Near-Field Analysis of Turbidity Flows Generated by Polymetallic Nodule Mining Tools. Mining. 2021; 1(3):251-278. https://doi.org/10.3390/mining1030017
Chicago/Turabian StyleElerian, Mohamed, Said Alhaddad, Rudy Helmons, and Cees van Rhee. 2021. "Near-Field Analysis of Turbidity Flows Generated by Polymetallic Nodule Mining Tools" Mining 1, no. 3: 251-278. https://doi.org/10.3390/mining1030017
APA StyleElerian, M., Alhaddad, S., Helmons, R., & van Rhee, C. (2021). Near-Field Analysis of Turbidity Flows Generated by Polymetallic Nodule Mining Tools. Mining, 1(3), 251-278. https://doi.org/10.3390/mining1030017






