Aggregated Gaze Data Visualization Using Contiguous Irregular Cartograms
Abstract
:1. Introduction
2. Related Work
2.1. Aggregated Gaze Data Visualization
2.2. Statistical Grayscale Heatmaps
2.3. Contiguous Irregular Cartograms
3. Materials and Methods
3.1. Gaze Data
3.2. Cartograms Implementation
3.3. Quantitative Evaluation Metrics
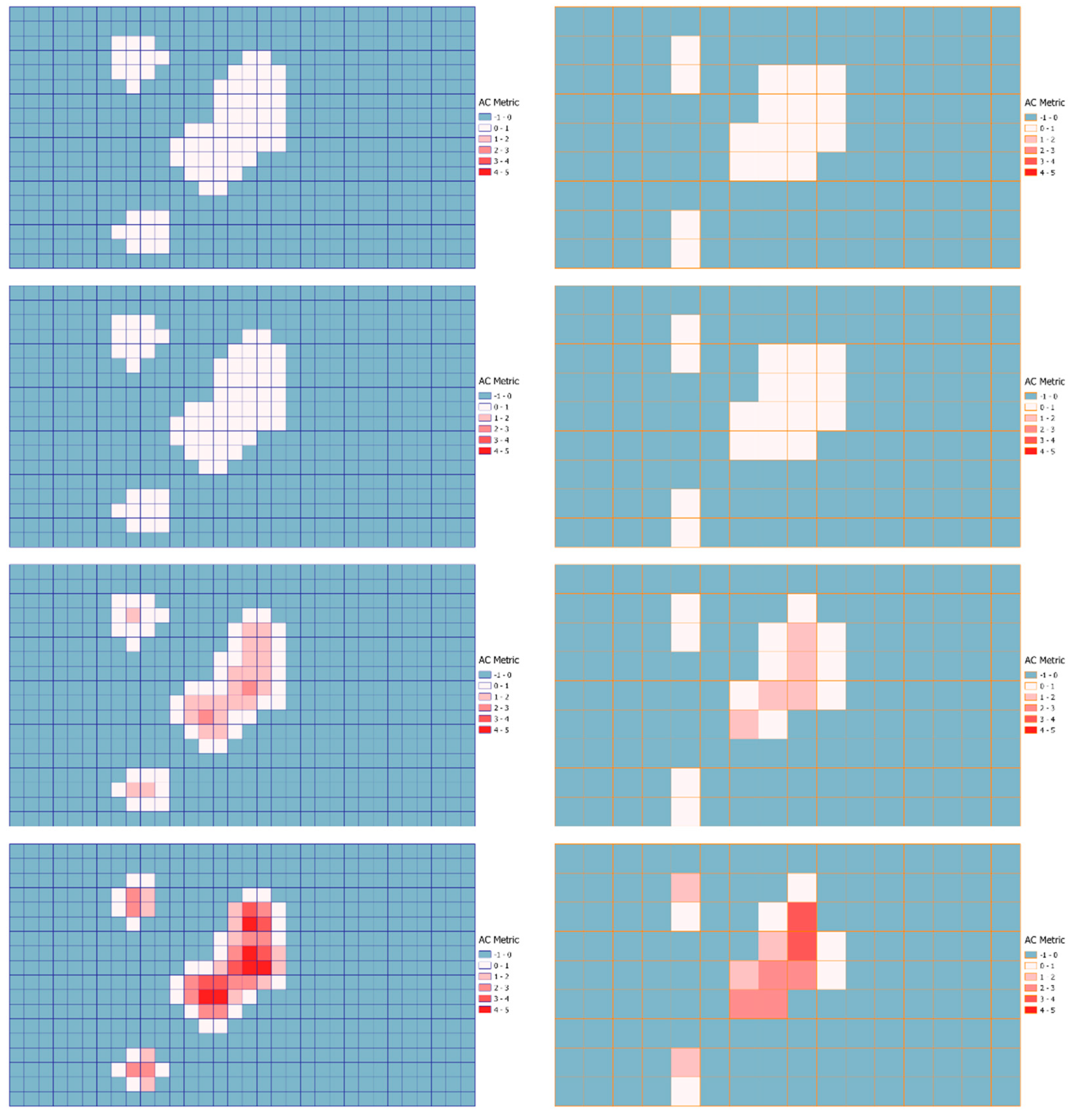
- CD metric: This metric refers to the cell’s center displacement after the implementation of the cartogram algorithm. For each corresponding cell, the CD can be computed as the Euclidean distance between two points: the geometric center of the cell before the transformation (first point) and the geometric center of the same cell after the transformation. Hence, the computation of CD metric is in distance units (e.g., in pixels). CD values are greater or equal to zero. A CD value equal to zero indicates that the geometric center of the cells remains constant after the topological transformation.
- AC metric: This metric refers to the area change between two corresponding cells (before and after the implementation of the cartogram algorithm). Therefore, this metric is computed using the formula (A2 − A1)/A1, where A1 and A2 correspond to the areas before and after the transformation accordingly. The AC can also be expressed as a percentage (%) if this ratio will be multiplied by the value of 100%. However, considering that bigger changes may have resulted in bigger AC values (greater than 100%) it is not always quite representative to express the metric as a percentage. Positive AC values indicate that the cell’s area increased after the transformation and negative AC values indicate that the area decreased. Zero values of AC indicate the absence of any area change.
4. Results
4.1. Aggregated Gaze Data Visualizations
4.2. CD and AC Metrics Visualizations
4.3. CD and AC Metrics Analysis
5. Discussion and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ashraf, H.; Sodergren, M.H.; Merali, N.; Mylonas, G.; Singh, H.; Darzi, A. Eye-tracking technology in medical education: A systematic review. Med. Teach. 2018, 40, 62–69. [Google Scholar] [CrossRef] [PubMed]
- Brunyé, T.T.; Drew, T.; Weaver, D.L.; Elmore, J.G. A review of eye tracking for understanding and improving diagnostic interpretation. Cogn. Res. Princ. Implic. 2019, 4, 7. [Google Scholar] [CrossRef]
- Alemdag, E.; Cagiltay, K. A systematic review of eye tracking research on multimedia learning. Comput. Educ. 2018, 125, 413–428. [Google Scholar] [CrossRef]
- Sharafi, Z.; Soh, Z.; Guéhéneuc, Y.-G. A systematic literature review on the usage of eye-tracking in software engineering. Inf. Softw. Technol. 2015, 67, 79–107. [Google Scholar] [CrossRef]
- Obaidellah, U.; Al Haek, M.; Cheng, P.C.-H. A survey on the usage of eye-tracking in computer programming. ACM Comput. Surv. 2018, 51. [Google Scholar] [CrossRef]
- Peißl, S.; Wickens, C.D.; Baruah, R. Eye-tracking measures in aviation: A selective literature review. Int. J. Aerosp. Psychol. 2018, 28, 98–112. [Google Scholar] [CrossRef]
- Strohmaier, A.R.; MacKay, K.J.; Obersteiner, A.; Reiss, K.M. Eye-tracking methodology in mathematics education research: A systematic literature review. Educ. Stud. Math. 2020, 104, 147–200. [Google Scholar] [CrossRef]
- Krassanakis, V.; Cybulski, P. A review on eye movement analysis in map reading process: The status of the last decade. Geod. Cartogr. 2019, 68, 191–209. [Google Scholar] [CrossRef]
- Sickmann, J.; Le, H.B.N. Eye-tracking in behavioural economics and finance—A literature review. Discuss. Pap. Behav. Sci. Econ. 2016, 2016, 1–40. [Google Scholar]
- Wedel, M. Attention research in marketing: A review of eye-tracking studies. In The Handbook of Attention; Boston Review: Cambridge, MA, USA, 2015; pp. 569–588. ISBN1 978-0-262-02969-8. (Hardcover); ISBN2 978-0-262-33187-6. (Digital (undefined format)). [Google Scholar]
- Scott, N.; Zhang, R.; Le, D.; Moyle, B. A review of eye-tracking research in tourism. Curr. Issues Tour. 2019, 22, 1244–1261. [Google Scholar] [CrossRef]
- Goldberg, J.H.; Helfman, J.I. Comparing information graphics: A critical look at eye tracking. In Proceedings of the 3rd BELIV’10 Workshop: BEyond Time and Errors: Novel EvaLuation Methods for Information Visualization, Atlanta, GA, USA, 10–11 April 2010; Association for Computing Machinery: New York, NY, USA, 2010; pp. 71–78. [Google Scholar]
- Ooms, K.; Krassanakis, V. Measuring the spatial noise of a low-cost eye tracker to enhance fixation detection. J. Imaging 2018, 4, 96. [Google Scholar] [CrossRef] [Green Version]
- Blascheck, T.; Kurzhals, K.; Raschke, M.; Burch, M.; Weiskopf, D.; Ertl, T. State-of-the-art of visualization for eye tracking data. In Proceedings of the EuroVis-STARs; Borgo, R., Maciejewski, R., Viola, I., Eds.; The Eurographics Association: Geneve, Switzerland, 2014. [Google Scholar]
- Burch, M.; Chuang, L.; Fisher, B.; Schmidt, A.; Weiskopf, D. Eye Tracking and Visualization: Foundations, Techniques, and Applications. ETVIS 2015, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 331947023X. [Google Scholar]
- Räihä, K.-J.; Aula, A.; Majaranta, P.; Rantala, H.; Koivunen, K. Static visualization of temporal eye-tracking data. In Proceedings of the Human-Computer Interaction—INTERACT 2005; Costabile, M.F., Paternò, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 946–949. [Google Scholar]
- Blascheck, T.; Kurzhals, K.; Raschke, M.; Burch, M.; Weiskopf, D.; Ertl, T. Visualization of eye tracking data: A taxonomy and survey. Comput. Graph. Forum 2017, 36, 260–284. [Google Scholar] [CrossRef]
- Voßkühler, A.; Nordmeier, V.; Kuchinke, L.; Jacobs, A.M. OGAMA (Open Gaze and Mouse Analyzer): Open-source software designed to analyze eye and mouse movements in slideshow study designs. Behav. Res. Methods 2008, 40, 1150–1162. [Google Scholar] [CrossRef] [Green Version]
- Krassanakis, V.; Filippakopoulou, V.; Nakos, B. EyeMMV toolbox: An eye movement post-analysis tool based on a two-step spatial dispersion threshold for fixation identification. J. Eye Mov. Res. 2014, 7. [Google Scholar] [CrossRef]
- Rodrigues, N.; Netzel, R.; Spalink, J.; Weiskopf, D. Multiscale scanpath visualization and filtering. In Proceedings of the 3rd Workshop on Eye Tracking and Visualization, Warsaw, Poland, 15 June 2018; Association for Computing Machinery: New York, NY, USA, 2018. [Google Scholar]
- Menges, R.; Kramer, S.; Hill, S.; Nisslmueller, M.; Kumar, C.; Staab, S. A visualization tool for eye tracking data analysis in the web. In Proceedings of the 2020 Symposium on Eye Tracking Research and Applications, Stuttgart, Germany, 2–5 June 2020; Association for Computing Machinery: New York, NY, USA, 2020. [Google Scholar]
- Špakov, O.; Miniotas, D. Visualization of eye gaze data using heat maps. Elektronika ir Elektrotechnika 2007, 74, 55–58. [Google Scholar]
- Bojko, A. Informative or misleading? Heatmaps deconstructed. In Human-Computer Interaction. New Trends; Jacko, J.A., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 30–39. [Google Scholar]
- Duchowski, A.T.; Price, M.M.; Meyer, M.; Orero, P. Aggregate gaze visualization with real-time heatmaps. In Proceedings of the Symposium on Eye Tracking Research and Applications, Santa Barbara, CA, USA, 28–30 March 2012; Association for Computing Machinery: New York, NY, USA, 2012; pp. 13–20. [Google Scholar]
- Kurzhals, K.; Hlawatsch, M.; Heimerl, F.; Burch, M.; Ertl, T.; Weiskopf, D. Gaze stripes: Image-based visualization of eye tracking data. IEEE Trans. Vis. Comput. Graph. 2016, 22, 1005–1014. [Google Scholar] [CrossRef]
- Burch, M.; Veneri, A.; Sun, B. Eyeclouds: A visualization and analysis tool for exploring eye movement data. In Proceedings of the 12th International Symposium on Visual Information Communication and Interaction, Shanghai, China, 20–22 September 2019; Association for Computing Machinery: New York, NY, USA, 2019. [Google Scholar]
- Kurzhals, K.; Weiskopf, D. Space-time visual analytics of eye-tracking data for dynamic stimuli. IEEE Trans. Vis. Comput. Graph. 2013, 19, 2129–2138. [Google Scholar] [CrossRef] [PubMed]
- Raschke, M.; Chen, X.; Ertl, T. Parallel scan-path visualization. In Proceedings of the Symposium on Eye Tracking Research and Applications, Santa Barbara, CA, USA, 28–30 March 2012; Association for Computing Machinery: New York, NY, USA, 2012; pp. 165–168. [Google Scholar]
- Burch, M.; Kumar, A.; Mueller, K. The hierarchical flow of eye movements. In Proceedings of the 3rd Workshop on Eye Tracking and Visualization, Warsaw, Poland, 15 June 2018; Association for Computing Machinery: New York, NY, USA, 2018. [Google Scholar]
- Burch, M.; Timmermans, N. Sankeye: A visualization technique for AOI transitions. In Proceedings of the ACM Symposium on Eye Tracking Research and Applications, Stuttgart, Germany, 2–5 June 2020; Association for Computing Machinery: New York, NY, USA, 2020. [Google Scholar]
- Krassanakis, V.; Menegaki, M.; Misthos, L.-M. LandRate toolbox: An adaptable tool for eye movement analysis and landscape rating. In Proceedings of the 3rd International Workshop on Eye Tracking for Spatial Research, Zurich, Switzerland, 14 January 2018; Kiefer, P., Giannopoulos, I., Göbel, F., Raubal, M., Duchowski, A.T., Eds.; ETH Zurich: Zurich, Switzerland, 2018. [Google Scholar]
- Krassanakis, V.; Da Silva, M.P.; Ricordel, V. Monitoring human visual behavior during the observation of unmanned aerial vehicles (UAVs) videos. Drones 2018, 2, 36. [Google Scholar] [CrossRef] [Green Version]
- Perrin, A.-F.; Krassanakis, V.; Zhang, L.; Ricordel, V.; Perreira Da Silva, M.; Le Meur, O. EyeTrackUAV2: A large-scale binocular eye-tracking dataset for UAV videos. Drones 2020, 4, 2. [Google Scholar] [CrossRef] [Green Version]
- Krassanakis, V.; Kesidis, A.L. MatMouse: A mouse movements tracking and analysis toolbox for visual search experiments. Multimodal Technol. Interact. 2020, 4, 83. [Google Scholar] [CrossRef]
- Nusrat, S.; Kobourov, S. The state of the art in cartograms. Comput. Graph. Forum 2016, 35, 619–642. [Google Scholar] [CrossRef] [Green Version]
- Ullah, R.; Mengistu, E.Z.; van Elzakker, C.P.J.M.; Kraak, M.-J. Usability evaluation of centered time cartograms. Open Geosci. 2016, 8. [Google Scholar] [CrossRef]
- Field, K. Cartograms. Geogr. Inf. Sci. Technol. Body Knowl. 2017, 2017. [Google Scholar] [CrossRef]
- Han, R.; Li, Z.; Ti, P.; Xu, Z. Experimental evaluation of the usability of cartogram for representation of GlobeLand30 data. ISPRS Int. J. Geo-Inf. 2017, 6, 180. [Google Scholar] [CrossRef] [Green Version]
- Hennig, B.D. Rediscovering the World: Map Transformations of Human and Physical Space; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 3642348475. [Google Scholar]
- Markowska, A. Cartograms—Classification and terminology. Pol. Cartogr. Rev. 2019, 51, 51–65. [Google Scholar] [CrossRef] [Green Version]
- Markowska, A.; Korycka-Skorupa, J. An evaluation of GIS tools for generating area cartograms. Pol. Cartogr. Rev. 2015, 47, 19–29. [Google Scholar] [CrossRef] [Green Version]
- Gastner, M.T.; Seguy, V.; More, P. Fast flow-based algorithm for creating density-equalizing map projections. Proc. Natl. Acad. Sci. USA 2018, 115, E2156–E2164. [Google Scholar] [CrossRef] [Green Version]
- Sun, S. Applying forces to generate cartograms: A fast and flexible transformation framework. Cartogr. Geogr. Inf. Sci. 2020, 47, 381–399. [Google Scholar] [CrossRef]
- Tobler, W. Thirty five years of computer cartograms. Ann. Assoc. Am. Geogr. 2004, 94, 58–73. [Google Scholar] [CrossRef]
- Mueller, M.; Smith, N.; Ghanem, B. A benchmark and simulator for UAV tracking. In Proceedings of the Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 8–16 October 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 445–461. [Google Scholar]
- Hennig, B.D. Gridded cartograms as a method for visualising earthquake risk at the global scale. J. Maps 2014, 10, 186–194. [Google Scholar] [CrossRef] [Green Version]
- Dougenik, J.A.; Chrisman, N.R.; Niemeyer, D.R. An algorithm to construct continuous area cartograms. Prof. Geogr. 1985, 37, 75–81. [Google Scholar] [CrossRef]
- Karagiorgou, S.; Krassanakis, V.; Vescoukis, V.; Nakos, B. Experimenting with polylines on the visualization of eye tracking data from observations of cartographic lines. In Proceedings of the 2nd International Workshop on Eye Tracking for Spatial Research, Vienna, Austria, 23 September 2014; Volume 1241. [Google Scholar]

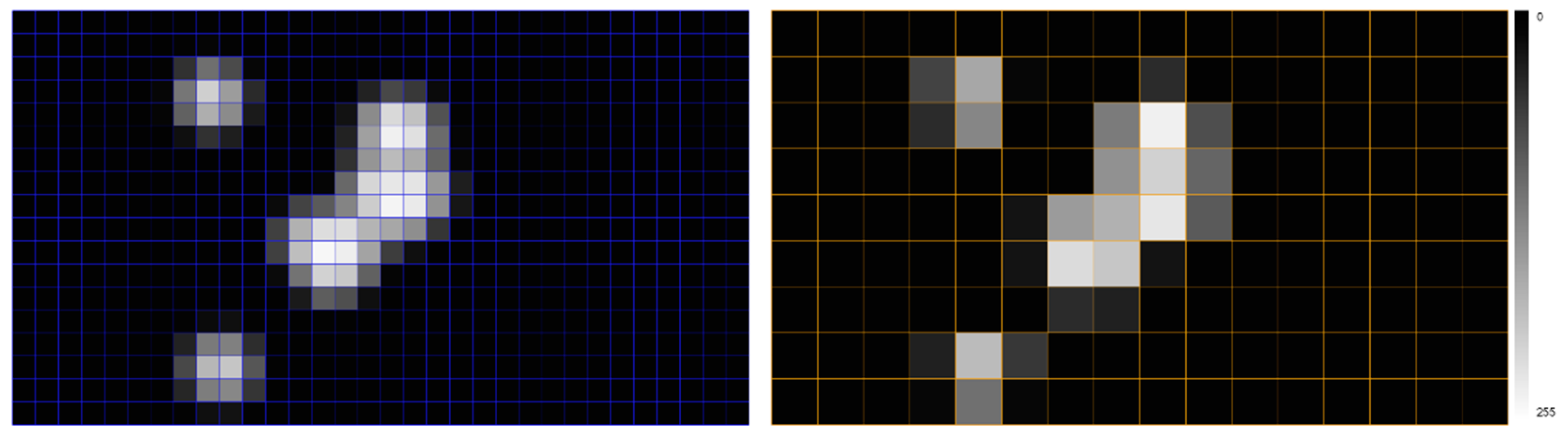


| Statistical Index | Values (Intensities) |
|---|---|
| Minimum | 0 |
| Maximum | 255 (28) |
| Mean | 10.41 |
| Median | 0 |
| Standard deviation | 35.30 |
| ‘heatmap40’ | ||||||||
| Statistical Index | CD (50) | CD (100) | CD (200) | CD (400) | AC (50) | AC (100) | AC (200) | AC (400) |
| Mean | 11.1 | 21.6 | 41.5 | 78.5 | −0.07 | −0.13 | −0.24 | −0.39 |
| Median | 10.7 | 20.8 | 40.0 | 75.6 | −0.11 | −0.21 | −0.40 | −0.70 |
| Standard deviation | 4.8 | 9.4 | 18.2 | 34.5 | 0.11 | 0.22 | 0.44 | 0.89 |
| Min value | 0.6 | 0.4 | 3.5 | 3.4 | −0.12 | −0.23 | −0.43 | −0.72 |
| Max value | 23.1 | 45.9 | 89.9 | 172.3 | 0.45 | 0.95 | 2.09 | 4.84 |
| ‘heatmap80’ | ||||||||
| Statistical Index | CD (50) | CD (100) | CD (200) | CD (400) | AC (50) | AC (100) | AC (200) | AC (400) |
| Mean | 10.7 | 20.9 | 40.2 | 75.6 | −0.07 | −0.13 | −0.24 | −0.40 |
| Median | 10.3 | 20.0 | 38.4 | 72.0 | −0.11 | −0.21 | −0.38 | −0.67 |
| Standard deviation | 4.6 | 9.1 | 17.3 | 32.3 | 0.10 | 0.20 | 0.39 | 0.77 |
| Min value | 1.1 | 2.7 | 6.1 | 12.7 | −0.13 | −0.24 | −0.46 | −0.79 |
| Max value | 19.9 | 39.7 | 78.4 | 150.9 | 0.36 | 0.75 | 1.59 | 3.20 |
| ‘heatmap40’ | ||||
| Threshold | 50 Iterations | 100 Iterations | 200 Iterations | 400 Iterations |
| CD values higher than the initial grid size (40 px) | 0.00% | 1.74% | 50.00% | 85.94% |
| Percentage of negative AC values | 88.02% | 88.02% | 88.19% | 88.72% |
| Percentage of positive AC values | 11.98% | 11.98% | 11.81% | 11.28% |
| Percentage of AC values correspond to higher than 20% change (negative or positive) | 5.38% | 83.68% | 94.27% | 97.05% |
| ‘heatmap80’ | ||||
| Threshold | 50 Iterations | 100 Iterations | 200 Iterations | 400 Iterations |
| CD values higher than the initial grid size (40 px) | 0.00% | 0.00% | 0.00% | 43.06% |
| Percentage of negative AC values | 87.50% | 87.50% | 88.19% | 88.89% |
| Percentage of positive AC values | 12.50% | 12.50% | 11.81% | 11.11% |
| Percentage of AC values correspond to higher than 20% change (negative or positive) | 4.17% | 72.22% | 90.97% | 93.75% |
| Heatmap | 50 Iterations | 100 Iterations | 200 Iterations | 400 Iterations |
|---|---|---|---|---|
| ‘heatmap40’ | −6.86% | −13.01% | −23.53% | −39.19% |
| ‘heatmap80’ | −6.86% | −13.04% | −23.65% | −39.66% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krassanakis, V. Aggregated Gaze Data Visualization Using Contiguous Irregular Cartograms. Digital 2021, 1, 130-144. https://doi.org/10.3390/digital1030010
Krassanakis V. Aggregated Gaze Data Visualization Using Contiguous Irregular Cartograms. Digital. 2021; 1(3):130-144. https://doi.org/10.3390/digital1030010
Chicago/Turabian StyleKrassanakis, Vassilios. 2021. "Aggregated Gaze Data Visualization Using Contiguous Irregular Cartograms" Digital 1, no. 3: 130-144. https://doi.org/10.3390/digital1030010
APA StyleKrassanakis, V. (2021). Aggregated Gaze Data Visualization Using Contiguous Irregular Cartograms. Digital, 1(3), 130-144. https://doi.org/10.3390/digital1030010





