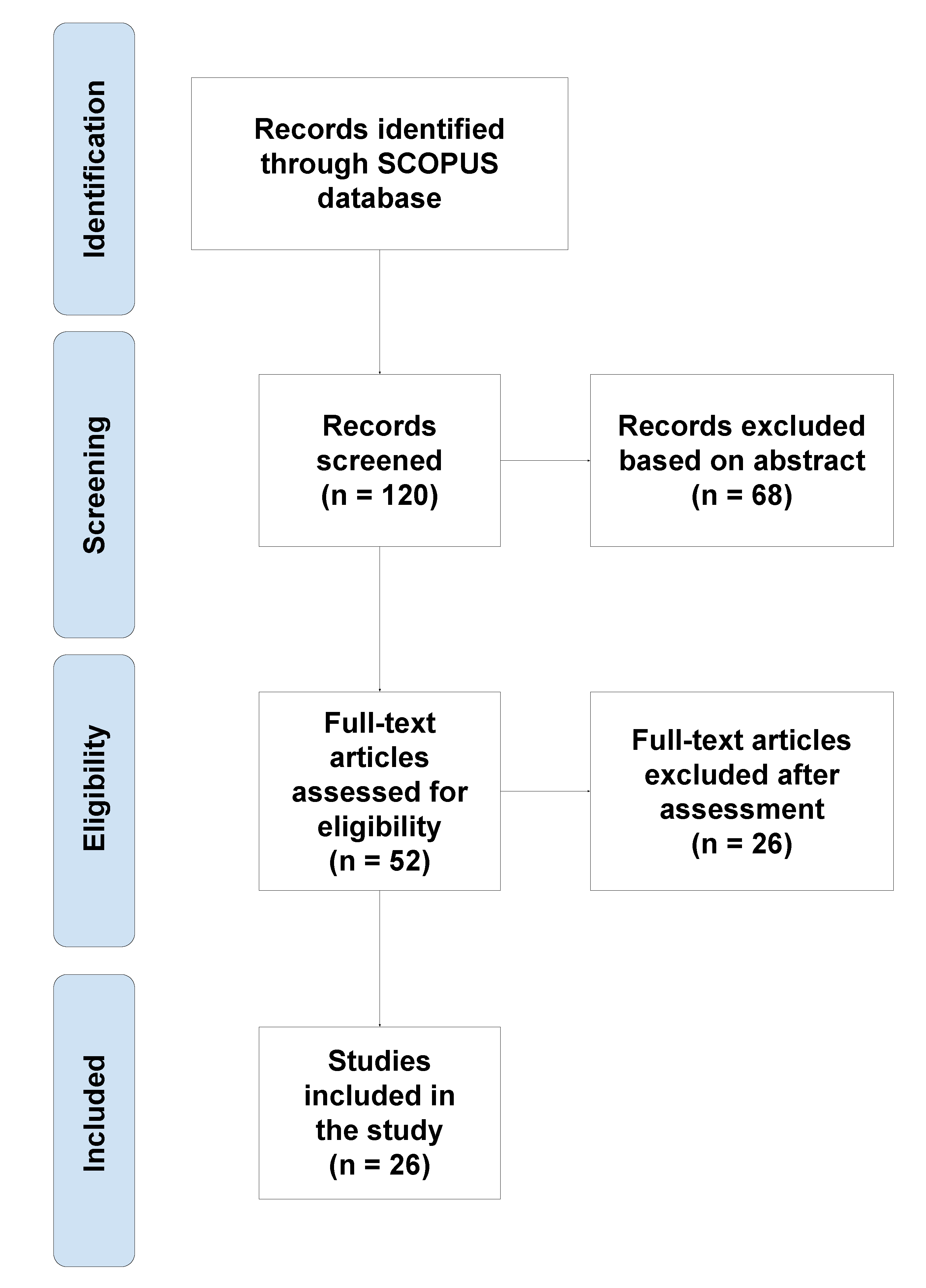
3.1. Category 1: Quantifying Space Similarity or Degree of Isomorphism
Zhang et al. [
10] proposed to view word embeddings as distributions and to minimize the divergence between them by minimizing their Earth Mover’s Distances (EMD). EMD measures the distance between two probability distributions. Their proposed method is unsupervised as they perform this minimization at the distribution level without any word level supervision. Two approaches are developed towards the fulfillment of their proposed idea: Wasserstein Generative Adversarial Network (WGAN) and EMD Minimization under Orthogonal Transformation (EMDOT). In the WGAN approach, a Generator transforms word embeddings in the source language into target space. The critic estimates the Wasserstein Distance between the transformed source embedding distributions and the target embedding distributions. This estimate is used by the Generator during training. The second approach, EMDOT, introduces an orthogonality constraint on the transformation matrix. It alternatingly optimizes a transport matrix and a transformation matrix while holding the other variables fixed. They also show correlation of Earth Mover’s Distance with typological and geographical dissimilarity between chosen languages and suggest it as a possible distance measure for quantifying linguistic differences. In comparing the two methods, the authors noted that EMDOT often converges to local minima while WGAN seems better at landing in the neighborhood of a good optimum. They report BLI results for five language pairs: Chinese–English, Spanish–English, Italian–English, Japanese–Chinese, and Turkish–English. They offer the low-resource setting of Turkish word embeddings as well as the morphological richness of Turkish as possible reasons for poor results in a Turkish–English BLI task.
Søgaard et al. [
7] introduced a metric in order to quantify similarity between word embeddings. They started out by establishing that word embeddings are, in fact, not isomorphic, even in the case of highly related languages such as English and German, in which the monolingual embeddings have been trained using the same hyperparameters. They do this by demonstrating the difference between the nearest neighbor graphs of the
k top words of both the English and German monolingual embedding spaces. The graphs built from the top
k English words and their German counterparts are not isomorphic as well. The same is true for the top
k nouns even though word embeddings are considerably adept at capturing relationship between nouns. For these reasons, the authors propose to measure the potential for unsupervised bilingual dictionary induction by capturing the degrees to which graphs are similar. They base their metric in Laplacian Eigenvalues. First, they build adjacency matrices from the nearest neighbor graphs of two monolingual embedding spaces. They then compute the eigensimilarity of the Laplacians by summing up the squared differences of the
k largest eigenvalues. They show strong correlation between BLI performance and their proposed graph similarity metric (0.89). They also propose utilizing identically spelled words present in both languages as a form of inexpensive supervision. They include Estonian, Finnish, Greek, Hungarian, Polish, and Turkish in addition to high-resource European languages in their experimental setup. The language choices were made in order to test whether BLI performance is affected by morphological complexities of the agglutinative languages with mixed or double markings. They investigated the impact of language similarity, among other factors, on BLI performance and reported poor performance for English–Finnish and English–Estonian pairs. To ensure that the results do not reflect the difference in training data size, they conducted another experiment using a large corpus for Finnish, which does not improve performance. Further experiments enabled the authors to opine that unsupervised learning between similar, mixed marking languages such as Finnish and Estonian are possible even though they fail when paired with English.
Sharoff et al. [
14] sought to extend the resources of a better resourced language to a lesser resourced one by translation matrix orthogonalization and generalized correction of hubness with Weighted Levenshtein Distance (WLD), which the authors propose as a measure of morphological structure. They proposed collecting a seed bilingual dictionary for lower resourced languages from interlinked Wikipedia article titles. To filter out aligned titles that are not necessarily cognates, the authors first used the estimated probabilities for characters present in the words in the seed dictionary to assess a rough WLD between the words. The translation suggestions were scored by a combination of cosine similarity and WLD. To incorporate weight adjustment resulting from the similarity between cognates into the cross lingual emebdding space, they selected the most similar words from the entire lexicons. This longer lexicon was produced from the cross-lingual embedding space using their WLD scores and then used to realign the existing alignment. This re-alignment process helps minimize the distance between known cognates and to preserve the orthogonality of the weight matrix. They reported BLI performance for the English–Italian pair. They also extracted a full set of possible cognates from a Panslavonic embedding space made up of Balto–Slavonic languages: Belorussian, Czech, Croatian, Lithuanian, Polish, Slovak, Slovene, and Ukrainian. Additionally, they reported Named Entity Recognition (NER) results for languages in the Panslavonic space.
Melis and Jaakkola [
15] cast the cross-lingual correspondence problem as an Optimal Transport problem. They built on the idea that metric recovery algorithms give rise to word embeddings and exploit Gromov–Wasserstein (GW) distance [
16] to measure the way similarities between word pairs reflect across languages. The GW distance measures how pairwise distances computed within different domains compare to each other. First, the pairwise distances on both the source and target sides were computed. Then, from the results of the first step, GW was computed, making it a quadratic problem. The authors also showed that the GW distance can be a measure of semantic discrepancy between languages. This notion of linguistic distance was based on the relational characterization of vector representation of words in different languages. The pairwise GW distances for word embedding similarity matrices of seven languages confirmed their intuition, where the cluster of Romance languages has the shortest distances among themselves while sharing a large distance to classical Chinese. Their approach has two optimization choices, the first of which is required only in large settings. Running their algorithms on full sets of embeddings is not feasible due to memory constraints. For their experiments, they chose to utilize 20,000 embeddings, which is the largest possible size for the personal computer they used. The other optimization choice is the entropy regularization parameter used in the Sinkhorn iteration of their algorithm. Larger values of this parameter,
, lead to smoother improvements with faster per-iteration runtime at a small decline in performance. Additionally, convergence is faster for calculation of GW distances between closer languages.
Xu et al. [
17] proposed to optimize a bidirectional transformation function between languages. To this end, they calculated the Sinkhorn distance [
18] as a measure of distributional similarity and minimized the back-translation losses. Their model takes the monolingual embedding spaces as inputs. Word embeddings are translated from one space to another by transfer functions, which are parameterized by neural networks. The Sinkhorn distance is calculated to measure the distributional similarity between the target space embeddings and the translated source space embeddings. This is performed for both embedding spaces. Similarly, back-translation loss is calculated for both spaces as well. The mapping functions were found to be sensitive to the initial parameter choices since the approach is completely unsupervised. The authors chose to minimize the optimal transport distance through adversarial training, using Wasserstein GAN. This first phase of adversarial training limits the search space for model parameters. The authors found that it boosts the training of their model despite being potentially unstable. They attributed the good results for their English–Spanish BLI task to the similarity between the languages and their training corpora being better aligned than any other language pairs. They also observed a performance difference between the two directions of the English–Italian language pair where Italian to English BLI performance is better than English to Italian. They attributed this discrepancy to there being more unique English words in the evaluation set. They also opined that translating from any other language to English would be easier because of there being multiple valid English equivalents for any word in the other language.
Chen and Cardie [
19] commented on the failure of unsupervised multilingual word embedding methods in leveraging the cross-lingual interdependencies and proposed a method that leverages the relation that exists between every language pair. Their two stage algorithm includes training multilingual word embeddings using the adversarial approach and then refining them with pseudo-supervision. For the first stage of their method, Multilingual Adversarial Training (MAT), they applied a series of language discriminators for each language in consideration. They learned the mappings by converting vectors from a random language space to another. The multilingual objective of these mappings leverages the relation between every language pair by confusing a language discriminator between its own vectors and those converted from other language spaces. For the refinement also, the authors proposed a generalized approach. Their proposed Multilingual Pseudo-Supervised Refinement (MPSR) induces a dictionary containing high-confidence translation pairs for all language pairs and uses it as weak-supervision to refine the initial mappings. They observed from their experimental results that pivoting through a third distant language when translating between similar languages degrades the performance. This observation is supported by the BLI task performances between Romance language pairs when they pivot through English. On the other hand, when the source and target languages are distant, a well-chosen pivot can improve the performance. Translation between German and Romance languages improves when English is utilized as the pivot language.
Artetxe et al. [
9] based their method on a fully unsupervised initialization that allows them to leverage the structural similarity between embeddings. Then, the solution is improved iteratively using a robust self-learning algorithm. Learning a fully unsupervised mapping between two independently trained monolingual embedding is especially challenging since the embedding matrices are unaligned along both dimensions. To solve this problem, they constructed similarity matrices of both the spaces. The matrix dimensions corresponded to words, thereby reducing the mismatch between the embedding spaces. Instead of trying to achieve matrix similarities in an approximate isometry, they sort the matrices and applied the nearest neighbor retrieval to find the translation pairs. Building the initial dictionary in this method lets them leverage the structural similarity between the monolingual embedding spaces. Their stochastic approach because of its dynamic convergence criterion is able to adapt to the difficulty of the task. One downside to this is that it takes longer to converge for difficult language pairs such as English–Turkish and English–Finnish. They reported a correlation between linguistic distance and execution time.
Zhang et al. [
20] observed that orthogonal mapping is effective for language pairs in which word embeddings are naturally isomorphic. They proposed a method called iterative normalization to facilitate orthogonal mapping for non-isomorphic language pairs. They noted that two embedding spaces are easily aligned if the word embeddings in those spaces are both length and center invariant. Length invariance serves the dual purpose of maintaining consistency of monolingual word embeddings and the objectives of the cross-lingual mapping, making alignment with translation pairs easier. The authors also proved that center invariance is a prerequisite for orthogonal alignment. In other words, the mean vectors of different languages should be of the same length for an orthogonal mapping to exist between them. Their proposed approach—Iterative Normalization—transforms monolingual word embeddings to be both length and center invariant. To do this, the vectors are mapped into unit vectors, and the collection of vectors is centered about their mean. From their experiments, they found that length and center invariance also help in learning linear non-orthogonal methods of learning cross lingual word embeddings.
Using the Gromov–Hausdorff (GH) distance, Patra et al. [
21] empirically demonstrated that the isometric assumption does not hold between embedding spaces, especially for language pairs that are etymologically distant. The Hausdorff distance measures the diametric distance between two metric spaces. Intuitively, this is the measure of the distance between nearest neighbors that are the furthest apart. Gromov–Hausdorff distance provides an estimate of isometry of two spaces by minimizing the Hausdorff distance over the possible isometric transforms between the two spaces. The authors proposed Bilingual Lexicon Induction with Semi-Supervision (BLISS), which optimizes for the weak orthogonality constraint as well as unsupervised matching of distribution and supervised alignment of embedding spaces. The unsupervised loss component of their proposed method aims to match the distributions of the source and target embedding distributions. They learned a transformation matrix to fool a discriminator trained to distinguish between mapped source embeddings and target embeddings. The supervised loss component of their method is computed by minimizing a similarity function that maximizes the similarity between given aligned bilingual word embeddings. BLISS also incorporates a weak orthogonality constraint in the form of a back-translation loss, which is particularly useful in cases of violation of the orthogonality constraint. Their semi-supervised method shows improvement over both the purely supervised and unsupervised baselines, especially for distant language pairs such as English and Chinese. They further reported observations of the small supervision contributing to the stabilization of the training process.
Zhou et al. [
22] proposed expressing the monolingual embedding spaces as probability densities. They matched these densities, defined by a Gaussian mixture model, using a method they call normalizing flow. In this method, they took samples from the Gaussian space at every step of training. By doing this, they moved away from training on fixed training samples. Apart from this idea, their approach consists of the following: the model was allowed to learn in both directions by allowing a back-translation loss along with weak supervision using identical strings and Gaussian mixture weights based on frequency matching. The weak orthogonality constraint introduced via back-translation encourages the mappings in both direction to be orthogonal to each other, which results in improved performance for the distant languages. They reported their empirical finding that Gaussian variance needs to be set higher for a language that is morphologically richer than the other in a language pair.
Grave et al. [
23] proposed Procustes in the Wassterstein distance, which is based on the estimation of an orthogonal matrix as well as a permutation matrix. The orthogonal matrix maps the points in the source space, while the permutation matrix helps infer the one-to-one correspondence of the mapped points with the target space points. The Wasserstein distance was chosen as a measure of distance between the two sets of points. They initialized the optimization algorithm with a convex relaxation traditionally used for the graph-isomorphism or graph-matching problem. The authors reported that the refinement procedure also helps improve performance for supervised approaches. They offered the noisy and small supervision lexicons as possible reasons for that. Another observation from their results is the impact of batch size on performance. A larger batch size results in better approximation of squared Wasserstein distance and the real loss function.
Beinborn and Choenni [
24] defined the correlation of distances between language families with the variation in the semantic organization of concepts across languages as semantic drift and proposed a method for quantifying it. Instead of relying on the availability of lexicon resources, they extracted translation pairs by taking the nearest semantic neighbor. First, they computed a similarity matrix for every word in the English space known as the representational similarity matrix. This symmetric matrix contains the cosine similarity between every pair of words. They then obtained translations of these English words in other languages by finding their nearest neighbor in the semantic space. Then, the representation similarity matrix was computed for the translated words in different languages. The Spearman correlation of the similarity vectors of these translation pairs expresses the similarity between them. The generalization of this measure was used to express similarity between language pairs. A second-order similarity matrix containing the similarity values between all the pairs of languages under consideration was then used to reconstruct a Phylogenatic tree. This tree was then evaluated against a “gold” tree to confirm its validity. The language clusters from word-based representational similarity are able to distinguish between Western and Eastern European languages as well as Germanic and Latin ones with the exception of English. The authors report that Indonesian, Hebrew, and Turkish are languages that do not fit well to the rest of the languages in the experimental setup. The authors observed that language contact is more crucial to semantic drift than a common ancestor language.
Zhang et al. [
25] sought to exploit the target side information while training an unsupervised multilingual word embedding space and proposed a novel Wasserstein GAN. This is based on an autoencoder that enables back-translations with the target side. A weak orthogonality constraint is imposed to learn the initial mappings in both directions. The initial mappings are learned by a Wasserstein GAN-based autoencoder where a generator tries generating fake target samples from source samples. A decoder tries to recover the original source sample while a discriminator fits the Wasserstein distance between the generated and target distributions. This choice sets their work in contrast to other similar works and enables learning a cross-lingual embedding space where the languages are etymologically distant from each other. The back-translation network takes the target side embeddings as input. The initial target-source and source-target mappings learned with weak orthogonality constraints are used as initializing weights between the input and the hidden layer and between the hidden layer and output layer of this back-translation network, respectively. The authors attributed the effectiveness of back-translation with target-side to the two-direction mapping preserving the target-side information for both sides, which cannot be achieved by one transformation matrix and its transpose. It also reuses the target-side samples and improves the quality of the cross lingual word embeddings by utilizing the underlying information. In analyzing the errors made by their system, they found that low-frequency words often obtain wrong translations. They opined that low-frequency words with poor semantic can appear as an outlier in the vector space, which would explain the phenomenon.
3.2. Category 2: Varying Hub Space or Pivot Language
Nakashole and Flauger [
26] proposed a knowledge distillation training objective that exploits translation paths for low-resource languages through higher resourced ones. Given that the target language is English, they utilized relatively larger seed dictionaries that a related language shares with both the source language and English to learn a transformation. For example, Spanish, which shares a larger seed dictionary with English and is highly related to Portuguese can be utilized to learn an improved mapping from Portuguese to English compared to using the small seed dictionary between Portuguese and English. Their approach makes the direct mapping from source to target language mimic the predictions made through the trilingual path as well as minimizes a loss function. They defined an additional objective that mimics the predictions through multiple trilingual paths. They reported BLI performances for their proposed trilingual paths where Portuguese, Afrikaans, and Danish distill from better-resourced Spanish, Dutch, and Swedish, respectively. They noted that multiple distillation paths require the model to optimize a more difficult function, which may influence the performance. They lost some of the performance gains when they add French and German to the distillation path opposed to when there was only one distillation path through Spanish from Portuguese to English. However, the path weights reflect the linguistic relations with the path through Spanish having the highest weight followed by French and German.
Doval et al. [
27] proposed applying a second transformation to refine the already aligned word embeddings in order to integrate them better with each other. The authors empirically demonstrated that there are significant gaps in the cross-lingual space between words and their translated equivalents. They credited this phenomenon to the constraints imposed upon the initial linear mapping that preserves the structure of the monolingual embeddings. Due to language and training corpora differences, this preservation of structure does not translate into optimal performance in downstream tasks. The authors proposed a method that brings each word pair closer together and makes them meet in the middle. The second mapping is learned from the same bilingual dictionary used to learn the initial mapping. The source word embeddings are now approximated to a point that is defined by the average of the source word embeddings and their respective translation embeddings in the cross-lingual space. While analyzing the source of errors in their BLI results, they found that some of the translated words are related to the gold reference word in the target language. They also observed that, after applying their additional transformation, the performance of the baselines improves and there are multiple instances of a translation changing from a closely related word in the target language to the gold reference itself.
Kementchedjhieva et al. [
28] proposed using Generalized Procustes Analysis (GPA) to map two languages onto a third latent space instead of onto each other. This approach makes approximating an alignment easier while yielding better performances in low-resource settings by incorporating supporting languages in the alignment process. The latent space captures properties of each of the embedding spaces as well as the ones that emerge as a result of the combination of the spaces. It is an average of the embedding spaces, which means it is more similar to these embedding spaces than they are to each other. As a result, it is easier to find a good mapping from the individual embedding spaces to the latent space than directly mapping one language space to another. According to the authors, GPA learns an alignment robust to morphologically and semantically related neighboring words as well as antonyms of the correct translations. They attributed the loss of precision to a suboptimal method that learns the alignment and a ceiling effect determining the best alignment that can be learned under the orthogonal constraint. To determine the latter, the authors performed a Procustes fit where they learn alignments in a completely supervised manner where the setup should ensure a 100% precision. The experiments confirmed a ceiling effect since Procustes fit is below 100% for all the language pairs in their experimental setup. The authors also observed a correlation between Procustes fit and precision scores for their weakly supervised GPA and attributed this to linguistic differences between source and target language as well as differences in respective training contents. GPA allows for the simultaneous alignment of three or four languages with the additional languages potentially providing support and boosting performance. They reported the BLI performance of this Multi-support GPA (MGPA) where Afrikaans, Bosnian, Estonian, Hebrew, and Occitan leverage the support of German, Russian, Finnish, Arabic, and Spanish, respectively, which are related languages with richer resources. The performance for Hebrew and Occitan improves in this setting.
Alaux et al. [
29] proposed to solve the degradation of translation quality for language pairs that do not involve the hub or the pivot language by mapping all vector sets to a common space. Instead of constraining the mappings directly, their formulation constrains every pair of vectors so that they are aligned well. Regarding the choice of alignment weights, they debated whether it is useful to constrain similar languages with higher weights as they already share similarities and whether increasing weights for distant languages might lead to difficulties in learning an alignment. They found simple weighting schemes to work best without making assumptions about linguistic similarities. They trained their models on 6 and 11 languages. The 11 languages were Czech, Danish, Dutch, English, French, German, Italian, Polish, Portuguese, Russian, and Spanish. The authors reported that adding new, distant languages does not affect the performance.
Heyman et al. [
30] pointed out the instability associated with fully unsupervised methods for inducing multilingual word embeddings and proposed a robust framework aimed at mitigating that. They proposed a regularization mechanism in order to find a more robust mapping for languages that are distant to the hub language. This mechanism leverages the structural similarity such a language shares with the rest of the languages in the embedding space. To that effect, they learned a shared space by adding new languages incrementally. They demonstrated that, by gradually adding languages, their method is able to leverage the interdependencies that exist between the languages already in the multilingual space and the new language. From their results, they deduced that adding distant languages later leads to better performance in such an iterative process. In comparing their two approaches, Single Hub Space (SHS) and Incremental Hub Space (IHS), they found that, for IHS, where the matrix growth is linear to the number of languages in the space, computation of SVD becomes more expensive. Value dropping [
9], which is a technique of avoiding suboptimal local minima by randomly dropping values from the matrix, also slows down the algorithms. The authors found that incrementally adding languages to a multilingual embedding space serves as a regularization process which, if coupled with adding distant languages later in the iteration, can make value dropping irrelevant for IHS. SHS with value dropping and IHS without it have similar training times.
Bai et al. [
31] proposed using a third, latent space for capturing cross-lingual features shared between monolingual word embeddings. They implemented their proposed method with a bilingual adversarial autoencoder. This architecture jointly transforms the source and target monolingual embedding space into the proposed latent space. The adversarial mechanism, along with a distance based objective function ensures that the transformed word embeddings are similar. They claimed that their proposed method is better suited to capture cross-lingual features. They also claimed that their proposed linear mapping with autoencoder constraint is an improvement over existing orthogonal mapping methods citing the weakness of the orthogonal assumption.
Lian et al. [
32] proposed to use the Wasserstein barycenter as a “mean” language to enforce the transitive relations between all language pairs in the multilingual embedding space. They reasoned that such a choice has more chances of capturing information related to all the languages than when English is chosen as a pivot language. In contrast to Alaux et al. [
29], who learn an arithmetic “mean”, which according to these authors, fails to preserve the distributional properties of different languages, a Wasserstein barycenter was learned. This Wasserstein metric captures the geometry of the distributions of different languages, and the barycenter can be considered a virtual universal language and, consequently, a pivot space. They report results from experiments they carried out to test whether including distant languages improve the BLI task accuracy. Their smaller experimental set included Indo-European languages: Croatian, English, French, German, and Italian. The larger experiment setup included two distant languages Finnish and Turkish. The reported accuracies for both the experimental setup show that translating through the barycenter of all the languages significantly improves the accuracies for several language pairs including German–Russian, English–Italian, English–Russian, English–Croatian, and Croatian–Russian. In cases where the latter setup sees decrease in accuracy, the performance is still comparable.
3.3. Category 3: Local Linear Maps or Non-Linear Global Map
Bai et al. [
33] noted that semantically similar words in distant language pairs need not be related by a linear relationship. They built on the idea of Faruqui and Dyer [
34] of using canonical correlation analysis to map the word embeddings of two languages in a shared vector space but aimed to instead capture a non-linear relationship using kernel canonical correlation analysis. By demonstrating performance improvements in evaluation tasks, they argued that the relationship between semantically equivalent words in different language can be captured better using non-linear relationships, especially in the cases of typologically distant languages.
Huang et al. [
35] went beyond word alignment and proposed alignment on a cluster level so that clusters of words have similar distribution across multiple languages. First, they augmented the monolingual word embeddings with their respective cluster of neighborhood words using an extension of the correlational neural network, CorrNet [
36], which were then aligned to form the common semantic space. CorrNet is an autoencoder-based approach of Common representation learning (CRL) that embeds different descriptions of the same data in a common subspace. Intuitively, this means that neighborhood of words are distributed consistently across languages so that mapping between the monolingual embedding spaces and the common semantic space is locally smooth. Language-independent character-level representations of words are also achieved using convolutional neural networks. These character-level representations are also concatenated with the word-level representations in the common space. Clusters are also built based on linguistic properties, which are once again aligned in the shared semantic space. Their approach is able to maintain performance even with a seed dictionary made up of 250 word pairs. They use low-resource name tagging to evaluate the quality of multilingual word embeddings. This task identifies named entities from text and classifies them into types such as Person (PER), Location (LOC), Organization (ORG), etc. They experimented on two sets of languages. The first one consists of Amharic and Tigrinya, languages that share the script (Ge’ez) and language family (proto-Semitic). The second one has English, Turkish, and Uighur, which are high-, medium-, and low-resource languages, respectively, and written in two scripts: Latin for English and Turkish, and Arabic for Uighur.
Nakashole [
37] proposed to capture the structural similarity of different languages by learning neighborhood sensitive maps. Instead of the original source language embedding space, they learned their mapping from its neighborhood sensitive representation. To this end, they first learned a dictionary of neighborhoods for the source language embeddings. The distinction of neighborhoods was encouraged by imposing an orthogonality constraint. This dictionary of neighborhoods was multiplied to the source language embeddings to obtain a representation factorized by the neighborhoods. Next, an intermediate representation was achieved by concatenating the factorized representation with the original embeddings. Finally, this intermediate representation was projected into a lower dimension equal to the original embeddings to obtain the final representation on which the transformation was learned. They stressed the significance for learning a neighborhood sensitive map for distant languages since a global linear map may not sufficiently capture the difference in underlying structures for such language embeddings. They noted that nouns and verbs constitute much of the test data and reported higher accuracy in translating nouns than verbs. They also interpreted the discovered neighborhoods. The top word neighborhoods obtained from training the English–German space seem to represent topics. The authors reported variation in the granularity of neighborhoods and their specificity. They report BLI performance on a new English–Portuguese dictionary containing rare words.
Nakashole and Faluger [
38] non-linearly mapped one language space to another. They asked whether a single linear map exists that produces comparable performance irrespective of where the translation embeddings fall in the target space. They also pondered over the possible relationship between neighborhood specific maps and the respective neighborhood distances. The experimental results showed that, in small enough neighborhoods, the transformation can be approximated by linear maps and that the amount by which local linear approximations vary correlate with the training neighborhood distances.
Moshtaghi et al. [
39] introduced noise tolerance to Generalized Procustes. Their method is fixed for rotational differences between a pair of embedding spaces and accounts for geometrical translation and dilation. In Euclidean geometry, translation denotes a change in location, whereas dilation denotes change in the size of a shape without the shape undergoing a change. Their model LLmap also allows for differences in linear mapping functions in different subspaces. This enables them to perform corrections specific to the regions in the embedding space. They achieved these two objectives by incorporating a noise-tolerant version of Generalized Procustes mapping, which they call Robust Generalized Procustes (RGP), into their Locally Linear Model. RGP enables them to add translation and dilation to the general Procustes. Additionally, they introduced a piece-wise linear mapping between two language spaces. This is based on a Locally Linear Neural Model (LLNF). By increasing the flexibility of the models in tackling the various levels of structural similarities encoded in the embbedding spaces, this model solves the undesired artifacts that may result from a global distance minimization. The computational complexity of the proposed mapping linearly increases with respect to the number of neurons. They dealt with this issue by limiting the number of neurons to four. On the other hand, finding the best dimension to split is the most expensive training step. The authors noted that this was performed as a preprocessing step.
Fan et al. [
40] proposed learning multiple mapping matrices with orthogonal constraint since, according to them, a single matrix may not be able to capture the complex linguistic regularities reflected in the semantics of words across different topics and domains. Each of these matrices capture the translation knowledge between two monolingual embedding spaces over distributed latent topics. To discover latent topics, they clustered the words in the source embedding space, resulting in a training set where each translation pair gets distributed across all the latent topics. Learning a single matrix for each of these latent topics harms the performance for low-resource languages. Instead of hard clustering, they introduced a soft piecewise mapping that determines a degree of membership of each translation pair to a number of latent topics predetermined through fine-tuning over the validation set. They reported BLI performance for English to and from Spanish, French, German, Italian, Chinese, and Vietnamese for general domain words. Additionally, they reported English–German and Chinese–English BLI performance for medical words and e-product words, respectively. From the reported results, the authors concluded that their proposed multiple mapping matrices improved BLI performance for low-frequency domain words.