A Neuro-Fuzzy Technique for the Modeling of β-Glucosidase Activity from Agaricus bisporus
Abstract
:1. Introduction
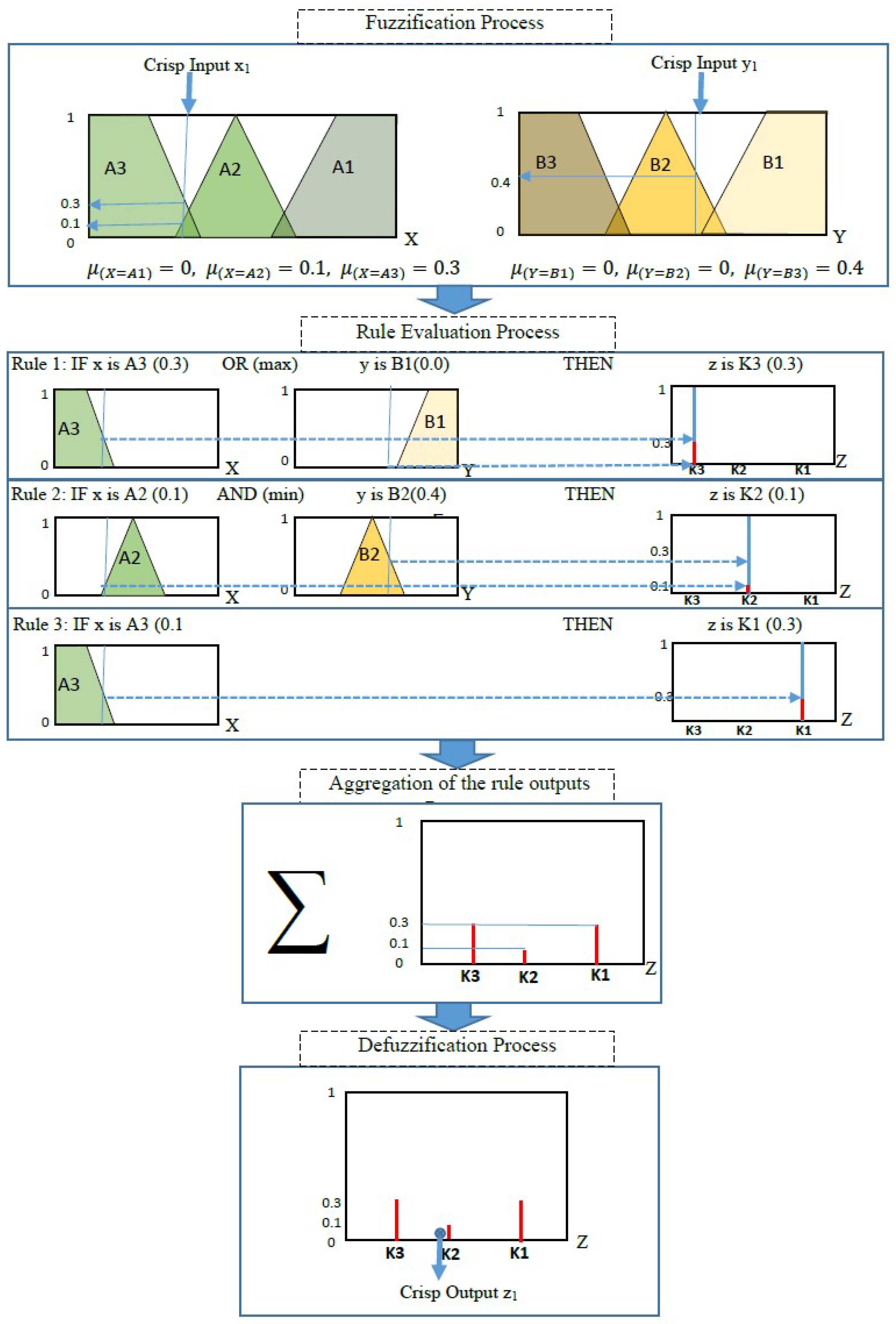
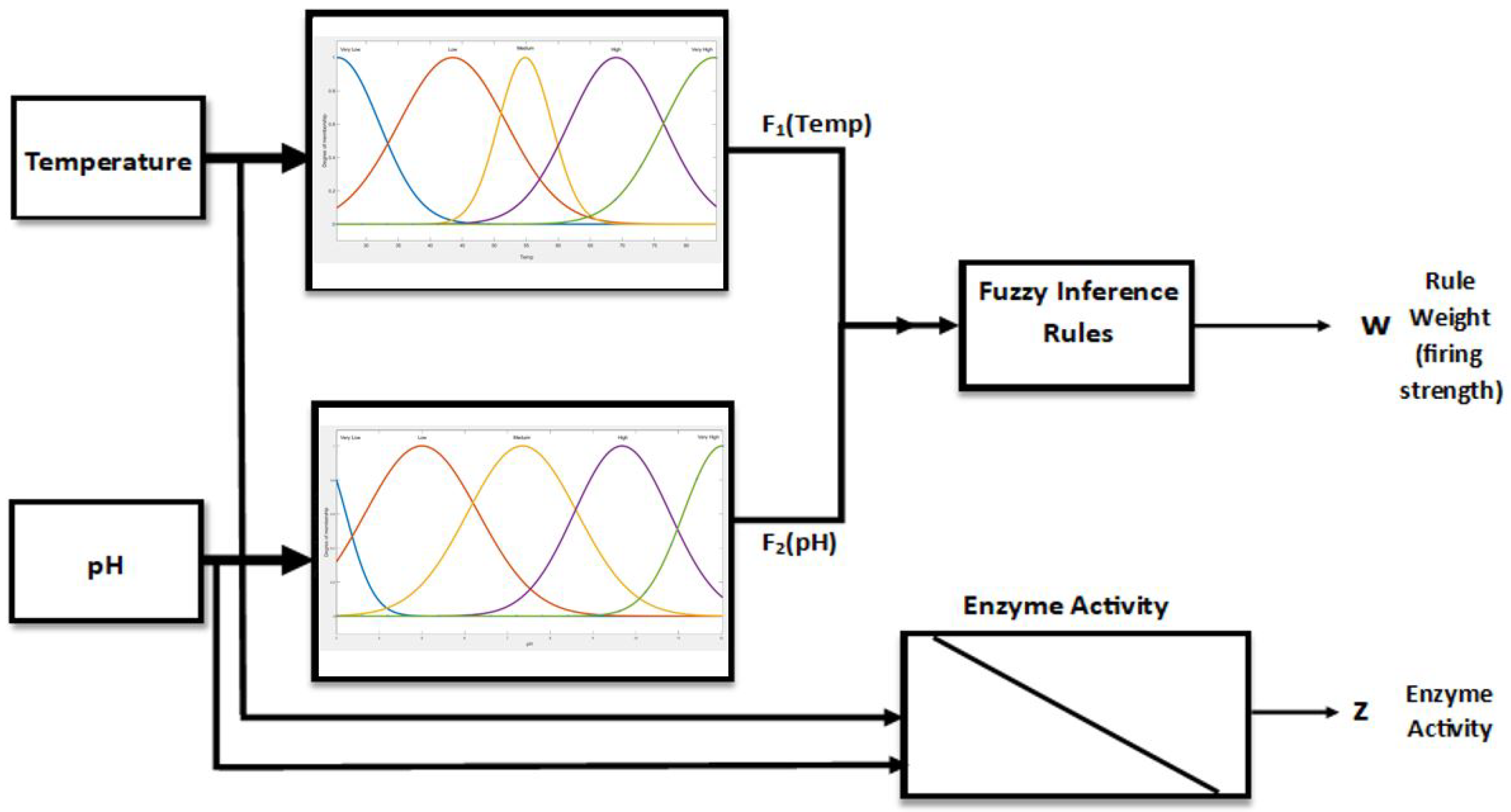
2. Neuro-Fuzzy Inference System
- The process of determining the degree to which the input variable belongs to each of the suitable fuzzy sets through membership functions, also known as the fuzzification process. The membership function (MF) designates a mapped membership value between 0 and 1 for each point (input value). This method creates fuzzy sets.
- Application of the fuzzy operator in the antecedent using logical operations (AND = min, OR = max, and NOT = additive complement).
- The implication from the antecedent to the consequent using if–then rules, where fuzzy sets and fuzzy operators are the subjects and verbs of fuzzy logic. Every rule has conjugated a weight that is applied to the value given by the antecedent. The weight value is within the range [0–1].
- The aggregation process of the consequent across the rules. The fuzzy sets representing the strength of each rule’s output are amalgamated into a single fuzzy set in a process called aggregation.
- The defuzzification process can be used to obtain a single output value from the output set using one of the following methods: centroid method, bisector method, middle of maxima method, largest of maximum, and smallest of maxima method.
3. Enzyme Activity Modeling Using ANFIS
3.1. Sugeno Fuzzy Inference Systems
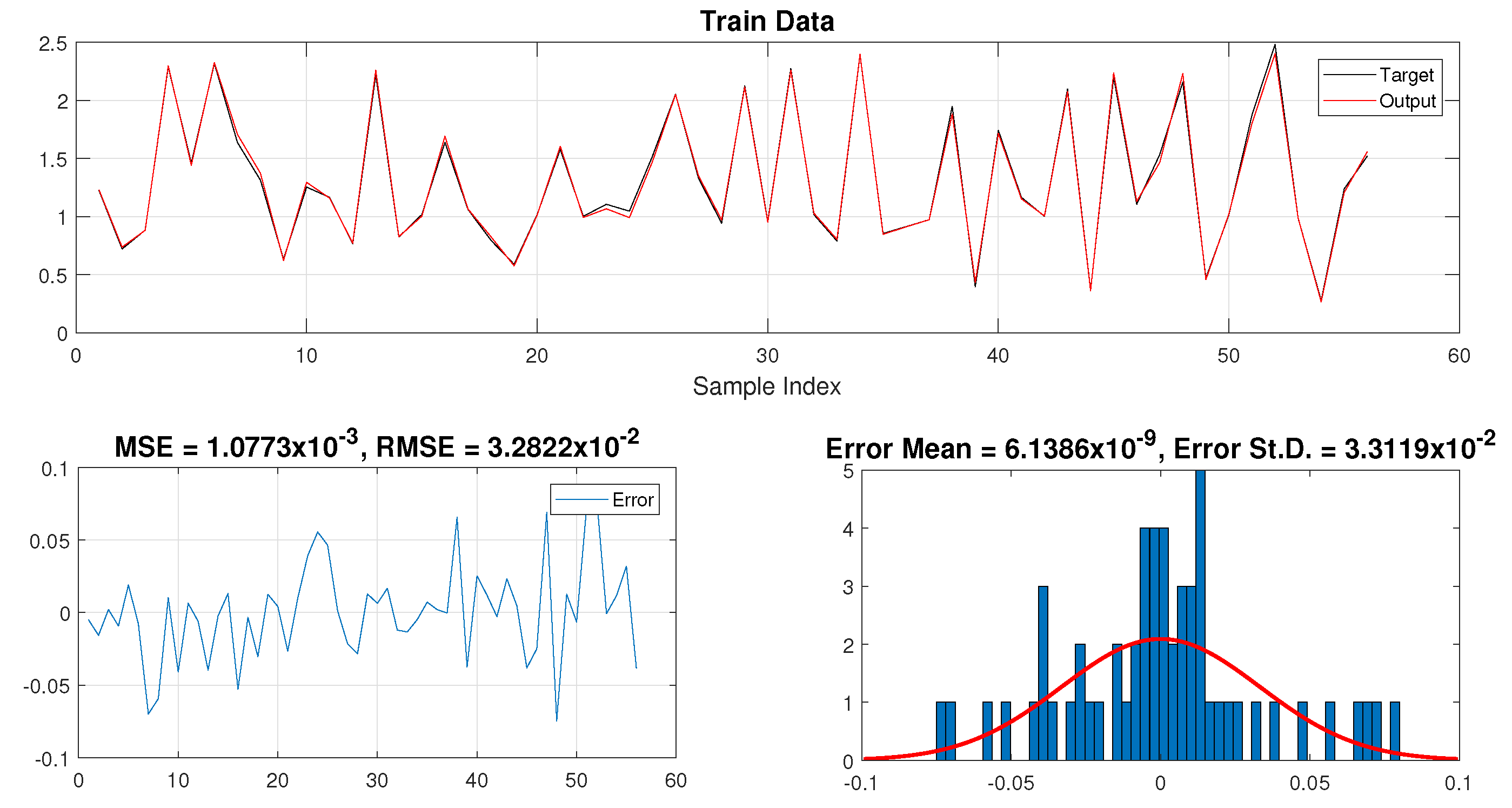
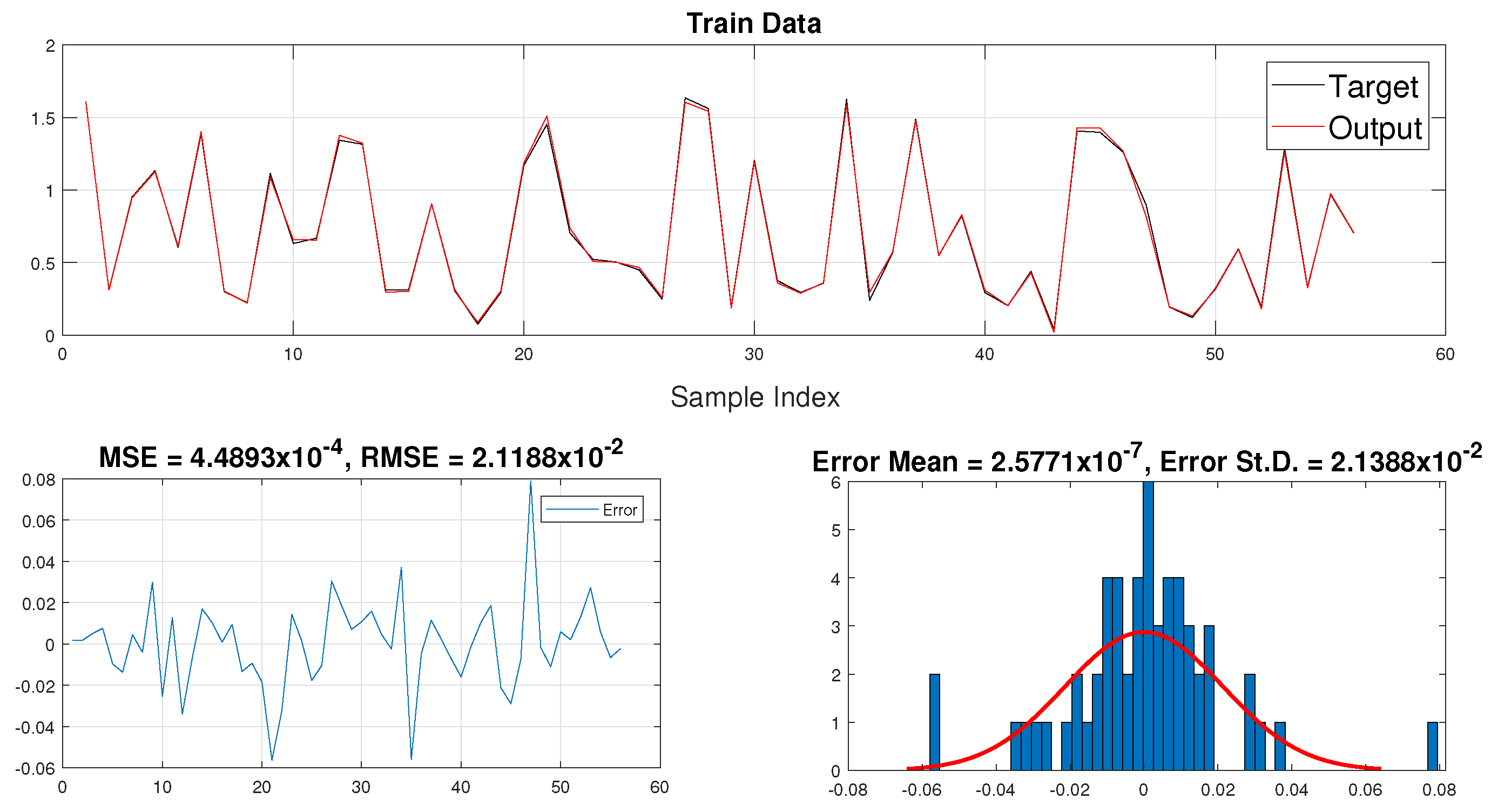
3.2. Training Data
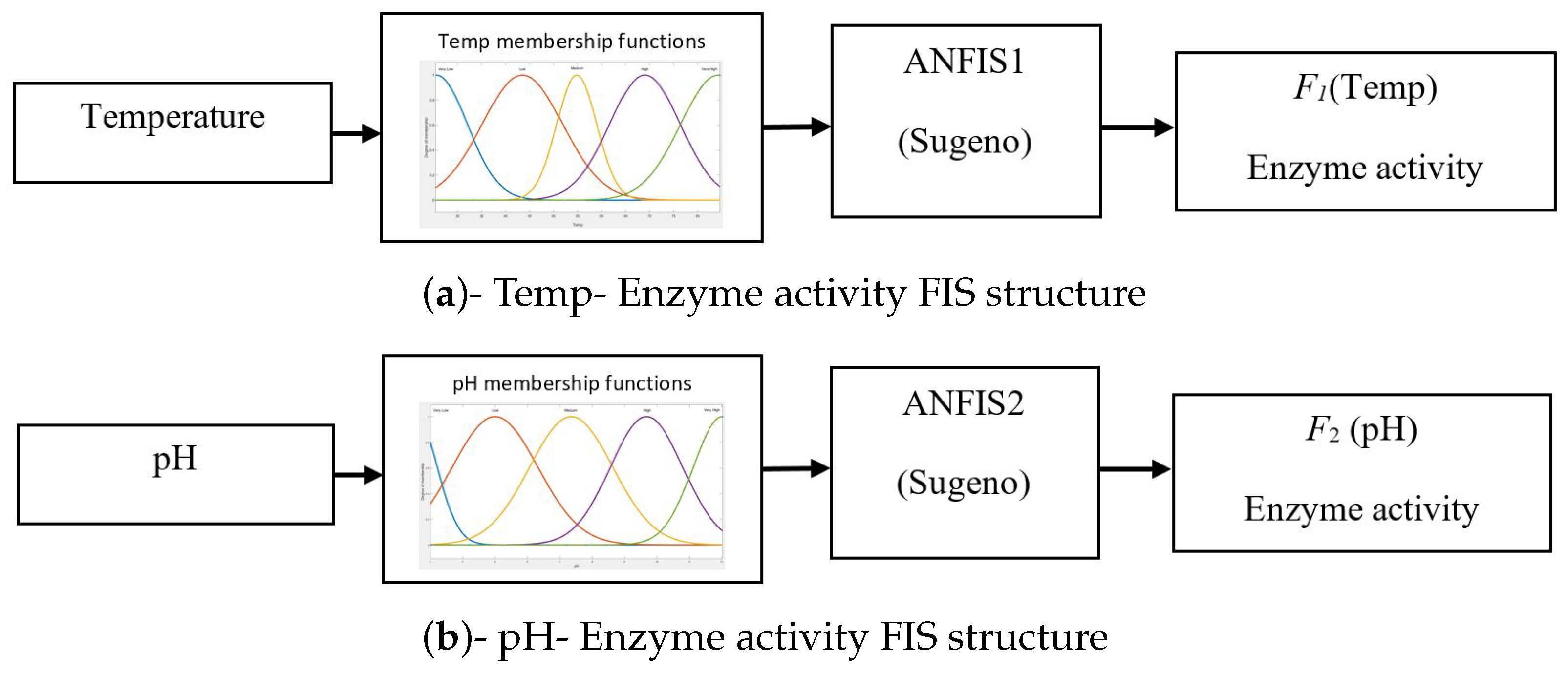
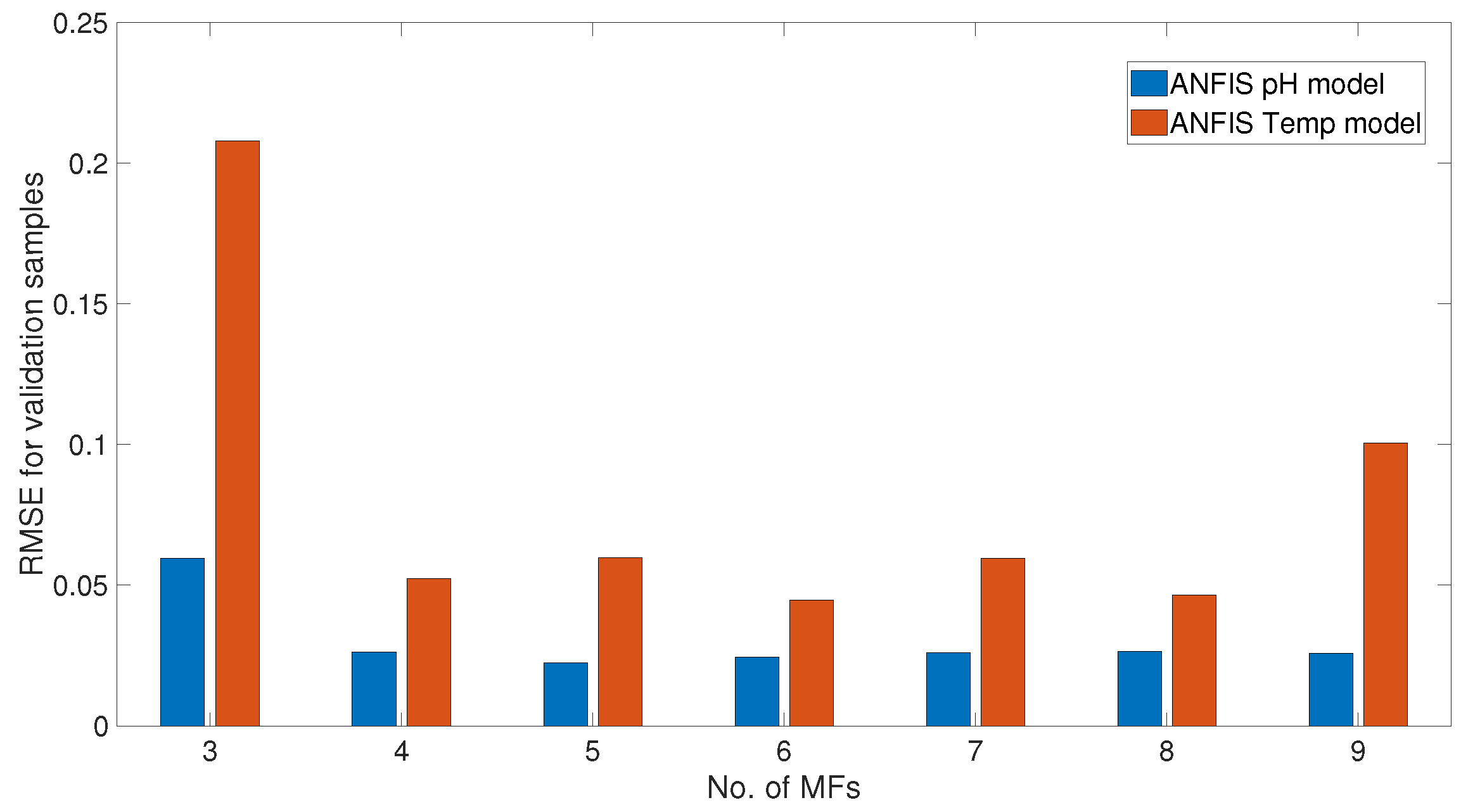
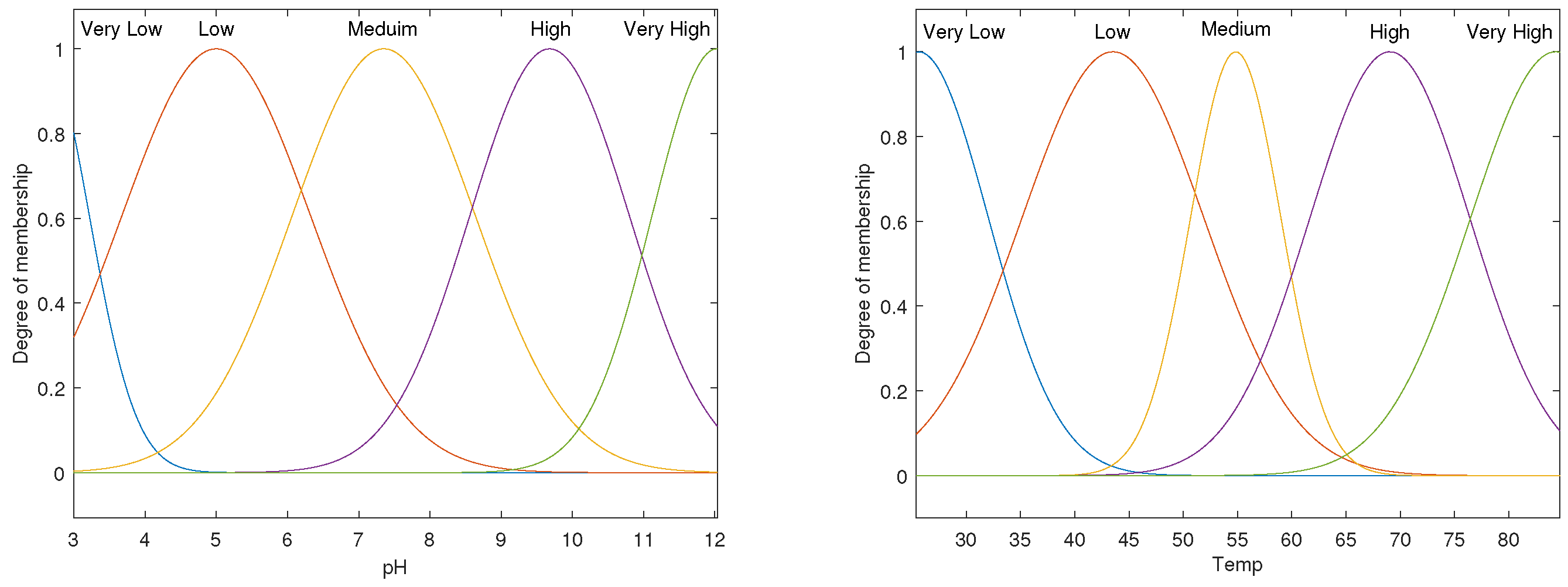
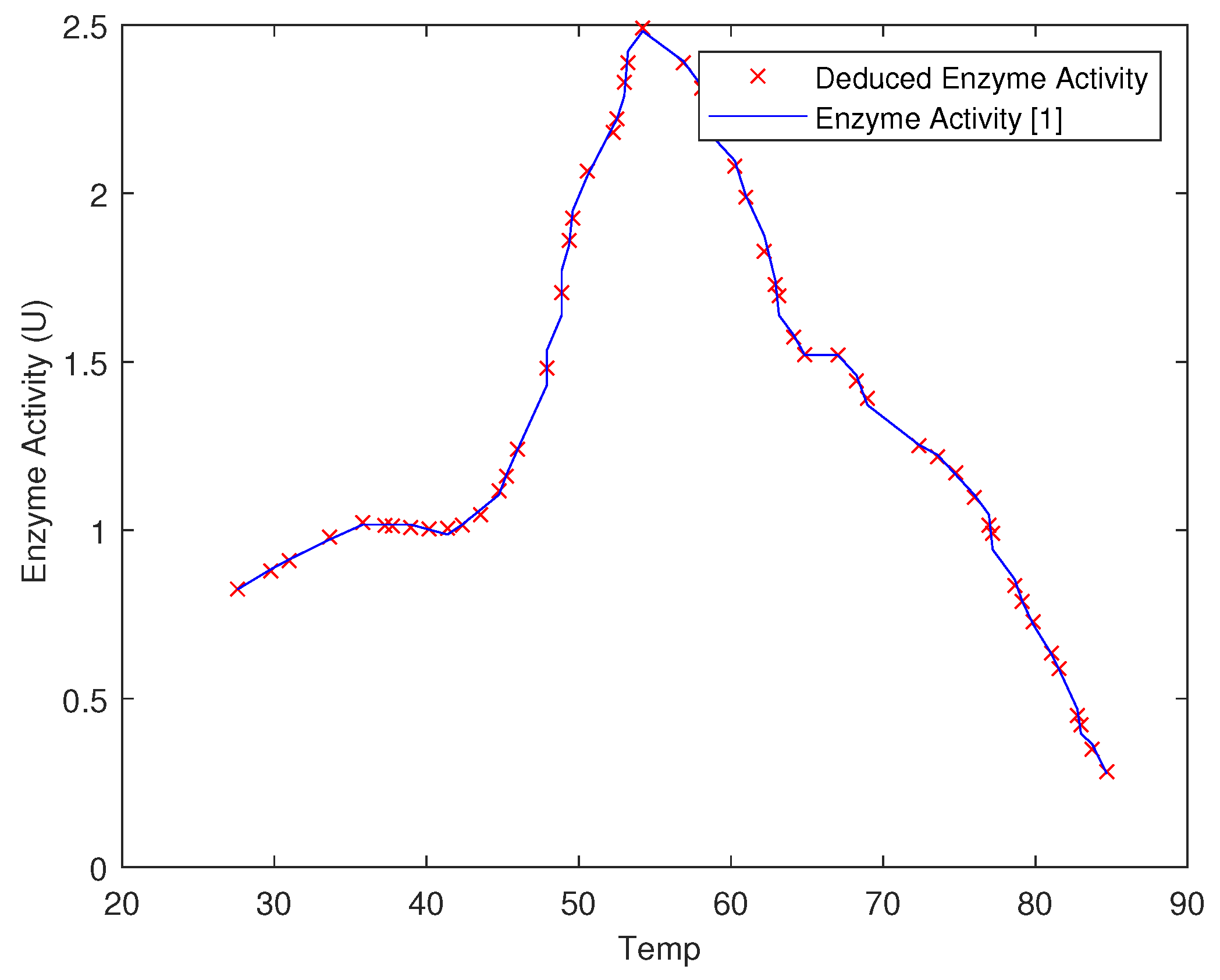
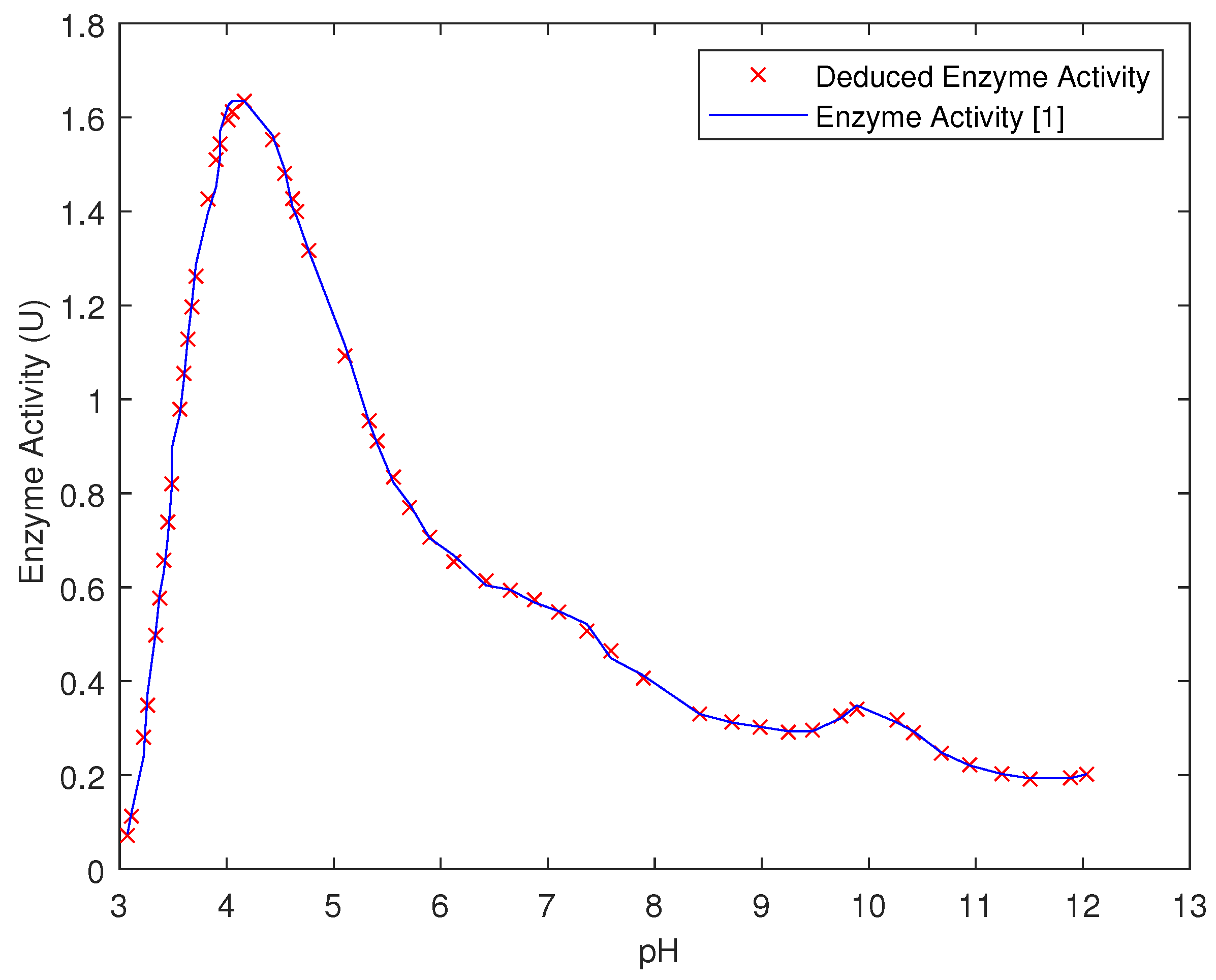
3.3. ANFIS Models for pH–Enzyme Activity and Temp–Enzyme Activity
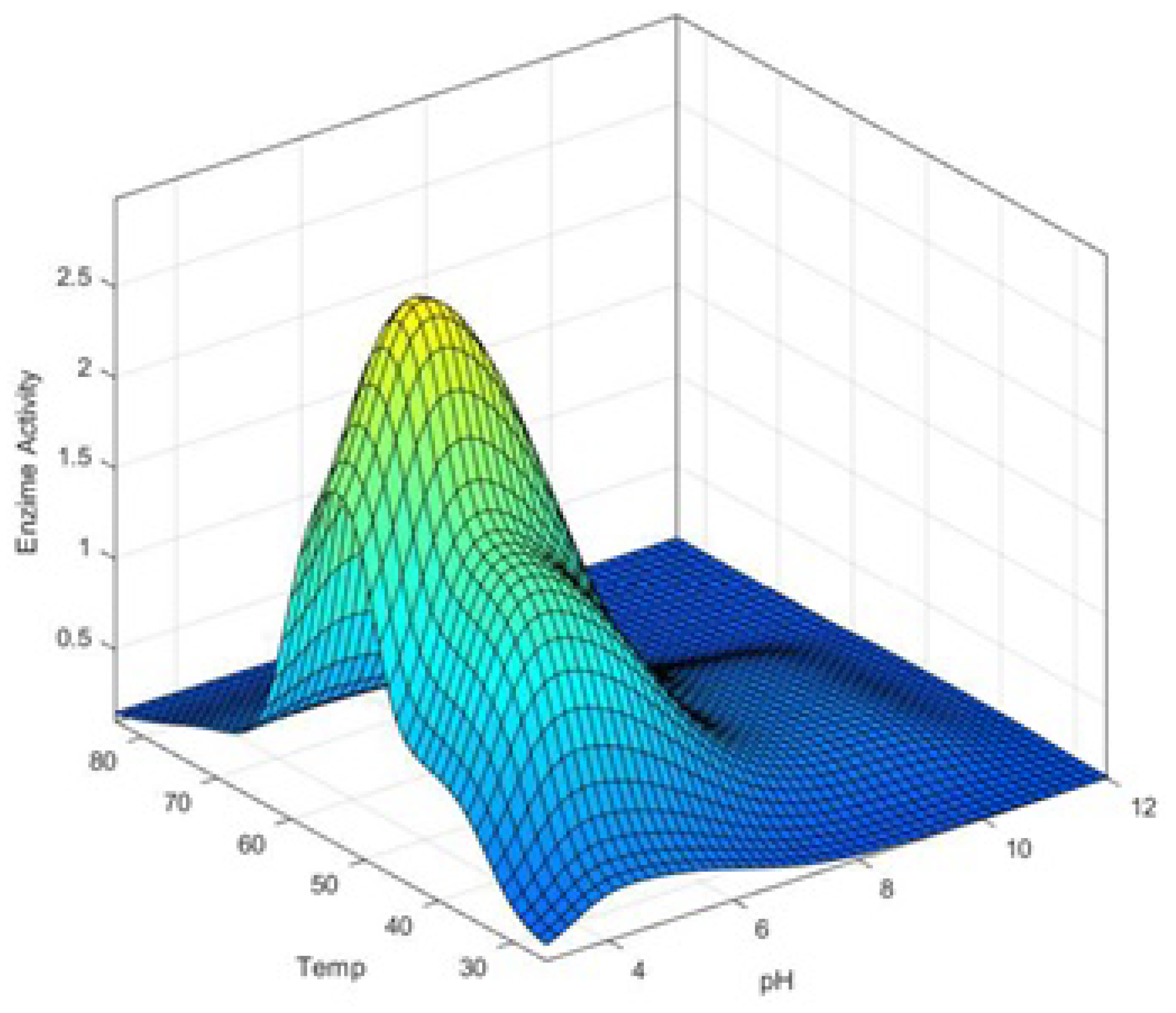
4. FIS Model for pH–Temp–Enzyme Activity
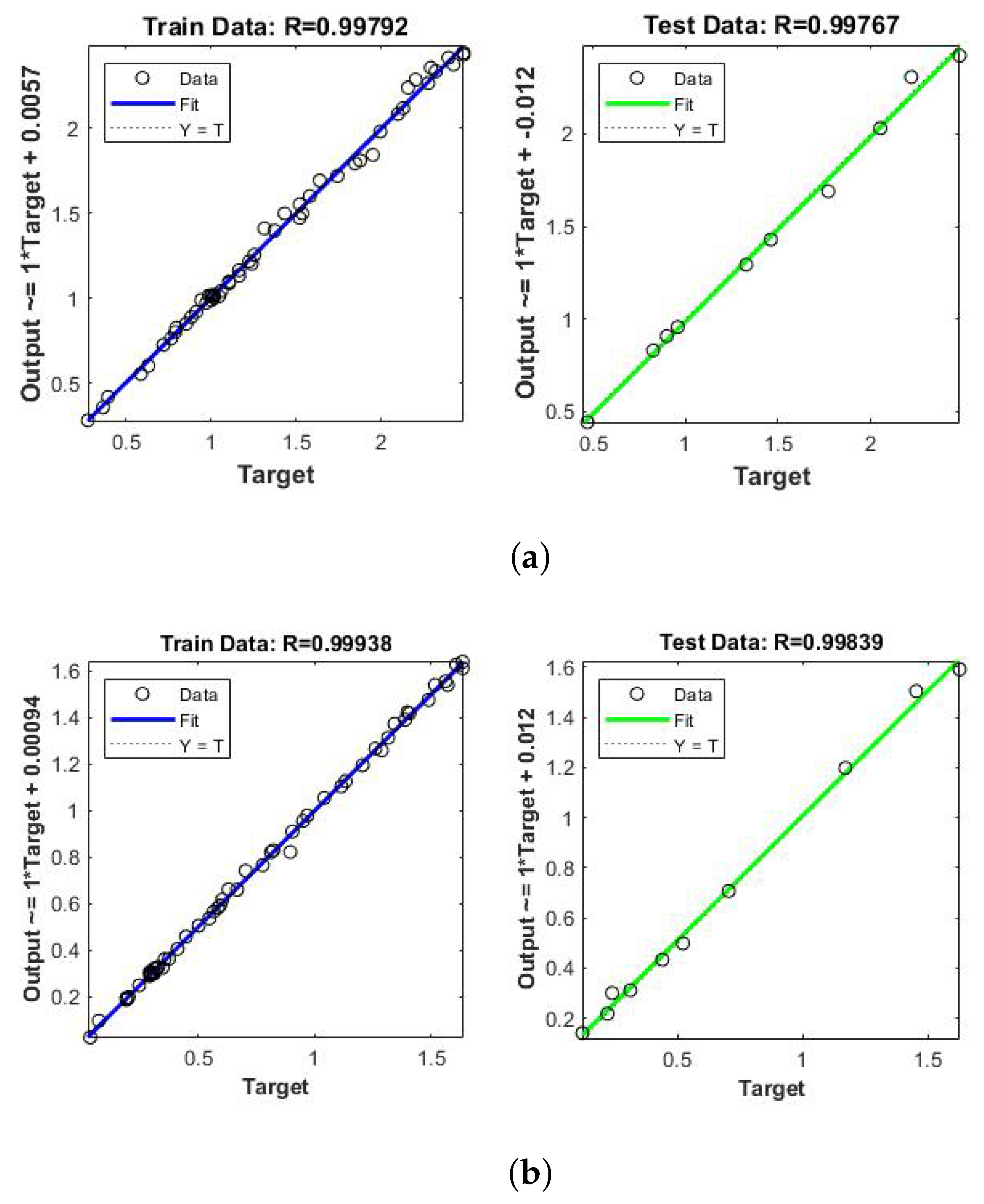
5. Results and Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ašić, A.; Bešić, L.; Muhović, I.; Dogan, S.; Turan, Y. Purification and Characterization of β-Glucosidase from Agaricus bisporus (White Button Mushroom). Protein J. 2015, 34, 453–461. [Google Scholar] [CrossRef] [PubMed]
- Singh, G.; Verma, A.K.; Kumar, V. Catalytic properties, functional attributes and industrial applications of β-glucosidases. Biotech 2016, 6, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Butters, T.D. Gaucher disease. Curr. Opin. Chem. Biol. 2007, 11, 412–418. [Google Scholar] [CrossRef]
- Hussein, A.A.; Al-Baer, A.S. Characterization and Cytotoxic Activity of Cytosine Deaminase Enzyme Purified from Locally Isolated Escherichia coli. Baghdad Sci. J. 2018, 15, 262–269. [Google Scholar] [CrossRef]
- Bhat, M.K.; Bhat, S. Cellulose degrading enzymes and their potential industrial applications. Biotechnol. Adv. 1997, 15, 583–620. [Google Scholar] [CrossRef]
- Abdellatif, F.H.H.; Babin, J.; Arnal-Herault, C.; David, L.; Jonquieres, A. Grafting cellulose acetate with ionic liquids for biofuel purification membranes: Influence of the anion. Carbohydr. Polym. 2018, 196, 176–186. [Google Scholar] [CrossRef]
- Godoy, M.G.; Amorim, G.M.; Barreto, M.S.; Freire, D.M.G. Agricultural Residues as Animal Feed: Protein Enrichment and Detoxification Using Solid-State Fermentation. In Current Developments in Biotechnology and Bioengineering; Elsevier: Amsterdam, The Netherlands, 2007; pp. 235–256. [Google Scholar] [CrossRef]
- Singhania, R.R.; Patel, A.K.; Sukumaran, R.K.; Larroche, C.; Pandey, A. Role and significance of beta-glucosidases in the hydrolysis of cellulose for bioethanol production. Bioresour. Technol. 2013, 127, 500–507. [Google Scholar] [CrossRef]
- Ahmed, A.; Nasim, F.U.-H.; Batool, K.; Bibi, A. Microbial β-Glucosidase: Sources, Production and Applications. J. Appl. Environ. Microbiol. 2017, 5, 31–46. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, N.; Rathour, R.; Jha, S.; Pandey, K.; Srivastava, M.; Thakur, V.K.; Sengar, R.S.; Gupta, V.K.; Mazumder, P.B.; Khan, A.F.; et al. Microbial Beta Glucosidase Enzymes: Recent Advances in Biomass Conversation for Biofuels Application. Biomolecules 2019, 9, 220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gueguen, Y.; Chemardin, P.; Janbon, G.; Arnaud, A.; Galzy, P. Investigation of the β-glucosidases potentialities of yeast strains and application to bound aromatic terpenols liberation. Stud. Org. Chem. 1998, 53, 149–157. [Google Scholar] [CrossRef]
- Gupta, A.; Kumar, V.; Dubey, A.; Verma, A.K. Kinetic Characterization and Effect of Immobilized Thermostable β -Glucosidase in Alginate Gel Beads on Sugarcane Juice. ISRN Biochem. 2014, 2014, 178498. [Google Scholar] [CrossRef] [Green Version]
- Jurado, E.; Camacho, F.; Luzón, G.; Vicaria, J.M. Kinetic models of activity for β-galactosidases: Influence of pH, ionic concentration and temperature. Enzym. Microb. Technol. 2004, 34, 33–40. [Google Scholar] [CrossRef]
- Joshi, A.; Palsson, B.O. Metabolic dynamics in the human red cell. Part III-Metabolic reaction rates. J. Theor. Biol. 1990, 142, 41–68. [Google Scholar] [CrossRef]
- Peskov, K.; Mogilevskaya, E.; Demin, O. Kinetic modelling of central carbon metabolism in Escherichia coli. FEBS J. 2012, 279, 3374–3385. [Google Scholar] [CrossRef] [PubMed]
- Smallbone, K.; Messiha, H.L.; Carroll, K.M.; Winder, C.L.; Malys, N.; Dunn, W.B.; Murabito, E.; Swainston, N.; Dada, J.O.; Khan, F.; et al. A model of yeast glycolysis based on a consistent kinetic characterisation of all its enzymes. FEBS Lett. 2013, 587, 2832–2841. [Google Scholar] [CrossRef]
- Saa, P.; Nielsen, L. Construction of feasible and accurate kinetic models of metabolism: A Bayesian approach. Sci. Rep. 2016, 6, 29635. [Google Scholar] [CrossRef] [PubMed]
- Hatzimanikatis, V.; Bailey, J.E. Effects of spatiotemporal variations on metabolic control: Approximate analysis using (log)linear kinetic models. Biotechnol. Bioeng. 1997, 54, 91–104. [Google Scholar] [CrossRef]
- Savageau, M.A. Biochemical systems analysis: I. Some mathematical properties of the rate law for the component enzymatic reactions. J. Theor. Biol. 1969, 25, 365–369. [Google Scholar] [CrossRef]
- Steuer, R.; Gross, T.; Selbig, J.; Blasius, B. Structural kinetic modeling of metabolic networks. Proc. Natl. Acad. Sci. USA 2006, 103, 11868–11873. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, S.; Cluett, W.R.; Mahadevan, R. Constructing kinetic models of metabolism at genome-scales: A review. Biotechnol. J. 2015, 10, 1345–1359. [Google Scholar] [CrossRef]
- Wojtusik, M.; Yepes, C.M.; Villar, J.C.; Cordes, A.; Arroyo, M.; Garcia-Ochoa, F.; Ladero, M. Kinetic modeling of cellobiose by a β-glucosidase from Aspergillus fumigatus. Carbohydr. Polym. 2018, 136, 502–512. [Google Scholar] [CrossRef]
- HHong, J.; Ladisch, M.R.; Gong, C.-S.; Wankat, P.C.; Tsao, G.T. Combined product and substrate inhibition equation for cellobiase. Biotechnol. Bioeng. 1981, 23, 2779–2788. [Google Scholar] [CrossRef]
- Bravo, V.; Páez, M.P.; Aoulad, M.; Reyes, A.; García, A.I. The influence of pH upon the kinetic parameters of the enzymatic hydrolysis of cellobiose with novozym 188. Biotechnol. Prog. 2001, 17, 104–109. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Yen, J.; Yang, L.; Liao, J.C. Incorporating qualitative knowledge in enzyme kinetic models using fuzzy logic. Biotechnol. Bioeng. 1999, 62, 722–729. [Google Scholar] [CrossRef]
- Nayak, P.C.; Sudheer, K.P.; Rangan, D.M.; Ramasastri, K.S. A neuro-fuzzy computing technique for modeling hydrological time series. J. Hydrol. 2004, 291, 52–66. [Google Scholar] [CrossRef]
- Ekici, L.; Simsek, Z.; Ozturk, I.; Sagdic, O.; Yetim, H. Effects of Temperature, Time, and pH on the Stability of Anthocyanin Extracts: Prediction of Total Anthocyanin Content Using Nonlinear Models. Food Anal. Methods 2014, 17, 1328–1336. [Google Scholar] [CrossRef]
- Zhu, X.L.; Jiang, Z.Y.; Wang, B.; He, Y.J. Decoupling control based on fuzzy neural-network inverse system in marine biological enzyme fermentation process. IEEE Access 2018, 6, 36168–36175. [Google Scholar] [CrossRef]
- Furlong, V.B.; Corrêa, L.J.; Giordano, R.C.; Ribeiro, M.P.A. Fuzzy-enhanced modeling of lignocellulosic biomass enzymatic saccharification. Energies 2019, 12, 2110. [Google Scholar] [CrossRef] [Green Version]
- Do, Q.H.; Chen, J.F. A neuro-fuzzy approach in the classification of students’ academic performance. Comput. Intell. Neurosci. 2013, 2013, 176–186. [Google Scholar] [CrossRef] [PubMed]
- Negnevitsky, M. Artificial Intelligence: A Guide to Intelligent Systems, 2nd ed.; Addison-Wesley: Boston, MA, USA, 2011. [Google Scholar]
- Fullér, R. Fuzzy neural networks. In Introduction to Neuro-Fuzzy Systems; Physica-Verlag HD; Springer: Berlin/Heidelberg, Germany, 2000; pp. 171–254. [Google Scholar] [CrossRef] [Green Version]
- Uzuner, S.; Çekmecelioğlu, D. Comparison of Artificial Neural Networks (ANN) and Adaptive Neuro-Fuzzy System (ANFIS) Models in Simulating Polygalacturonase Production. Enzym. Model. Bioresour. 2016, 11, 8676–8685. [Google Scholar] [CrossRef] [Green Version]
- Karaman, S.; Ozturk, I.; Yalcin, H.; Kayacier, A.; Sagdic, O. Comparison of adaptive neuro-fuzzy inference system and artificial neural networks for estimation of oxidation parameters of sunflower oil added with some natural byproduct extracts. J. Sci. Food Agric. 2012, 92, 49–58. [Google Scholar] [CrossRef] [PubMed]
- Sreekumar, S.; Kallingal, A.; Mundakkal Lakshmanan, V. Adaptive neuro-fuzzy approach to sodium chlorate cell modeling to predict cell pH for energy-efficient chlorate production. Chem. Eng. Commun. 2020, 208, 256–270. [Google Scholar] [CrossRef]
- Fullér, R. Fuzzy systems. In Introduction to Neuro-Fuzzy Systems; Physica-Verlag HD; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–131. [Google Scholar] [CrossRef] [Green Version]
- The MathWorks I. ANFIS: Adaptive-Network-Based Fuzzy Inference Systems. Mamdani Sugeno Fuzzy Inference Syst. 2020. Available online: https://www.mathworks.com/help/fuzzy/types-of-fuzzy-inference-systems.html (accessed on 18 December 2020).
- Cartwright, H. Using Artificial Intelligence in Chemistry and Biology, 1st ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: Adaptive-Network-based Fuzzy Inference Systems. IEEE Trans. Syst. Man Cybermetics 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Non-Linear Regression GUI-File Exchange-MATLAB Central. 2020. Available online: https://www.mathworks.com/matlabcentral/fileexchange/52968-nonlinear-regression-using-anfis-in-matlab (accessed on 18 December 2020).
| Temp | pH | Very Low | Low | Medium | High | Very High |
|---|---|---|---|---|---|---|
| Very Low | 2 | 3 | 1 | 1 | 1 | |
| Low | 3 | 4 | 2 | 2 | 1 | |
| Medium | 4 | 5 | 2 | 2 | 2 | |
| High | 3 | 4 | 2 | 1 | 1 | |
| Very High | 2 | 3 | 1 | 1 | 1 |
| Test # | pH | Temp | Deduced Enzyme Activity (U) | Enzyme Activity (U) | Error % |
|---|---|---|---|---|---|
| °C | MISO Model | Ref [1] | |||
| 1 | 3.5 | 37 | 0.89 | 0.829 | 6.853933 |
| 2 | 4.5 | 37 | 1.48 | 1.51 | 2.027027 |
| 3 | 5.5 | 37 | 0.822 | 0.8 | 2.676399 |
| 4 | 6.5 | 37 | 0.603 | 0.6 | 0.497512 |
| 5 | 7.5 | 37 | 0.448 | 0.42 | 6.25 |
| 6 | 5.5 | 30 | 0.898 | 0.83 | 7.572383 |
| 7 | 5.5 | 40 | 1.0019 | 0.99 | 1.187743 |
| 8 | 5.5 | 50 | 2.1 | 2.15 | 2.380952 |
| 9 | 5.5 | 60 | 2.05 | 2.1 | 2.439024 |
| 10 | 5.5 | 70 | 1.4 | 1.29 | 7.857143 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ansaf, H.; Ansaf, B.K.; Al Samahi, S.S. A Neuro-Fuzzy Technique for the Modeling of β-Glucosidase Activity from Agaricus bisporus. BioChem 2021, 1, 159-173. https://doi.org/10.3390/biochem1030013
Ansaf H, Ansaf BK, Al Samahi SS. A Neuro-Fuzzy Technique for the Modeling of β-Glucosidase Activity from Agaricus bisporus. BioChem. 2021; 1(3):159-173. https://doi.org/10.3390/biochem1030013
Chicago/Turabian StyleAnsaf, Huda, Bahaa Kazem Ansaf, and Sanaa S. Al Samahi. 2021. "A Neuro-Fuzzy Technique for the Modeling of β-Glucosidase Activity from Agaricus bisporus" BioChem 1, no. 3: 159-173. https://doi.org/10.3390/biochem1030013
APA StyleAnsaf, H., Ansaf, B. K., & Al Samahi, S. S. (2021). A Neuro-Fuzzy Technique for the Modeling of β-Glucosidase Activity from Agaricus bisporus. BioChem, 1(3), 159-173. https://doi.org/10.3390/biochem1030013






