RAMPA Therapy: Impact of Suture Stiffness on the Anterosuperior Protraction of Maxillae; Finite Element Analysis
Abstract
1. Introduction
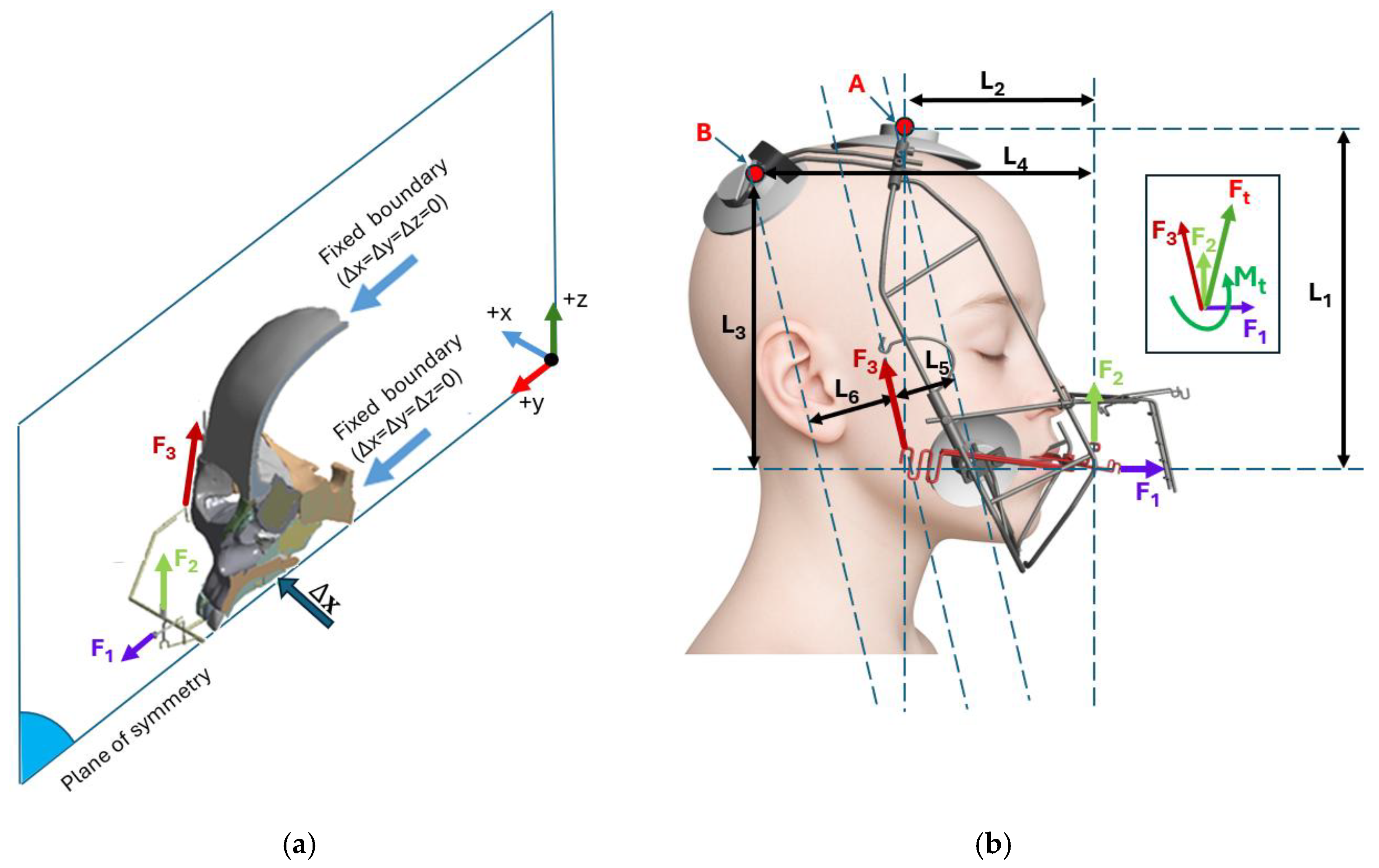
2. Materials and Methods
2.1. Skull Model Generation
2.2. Meshing and Finite Element Analysis
2.3. Orthodontic Appliances: RAMPA and gHu-1
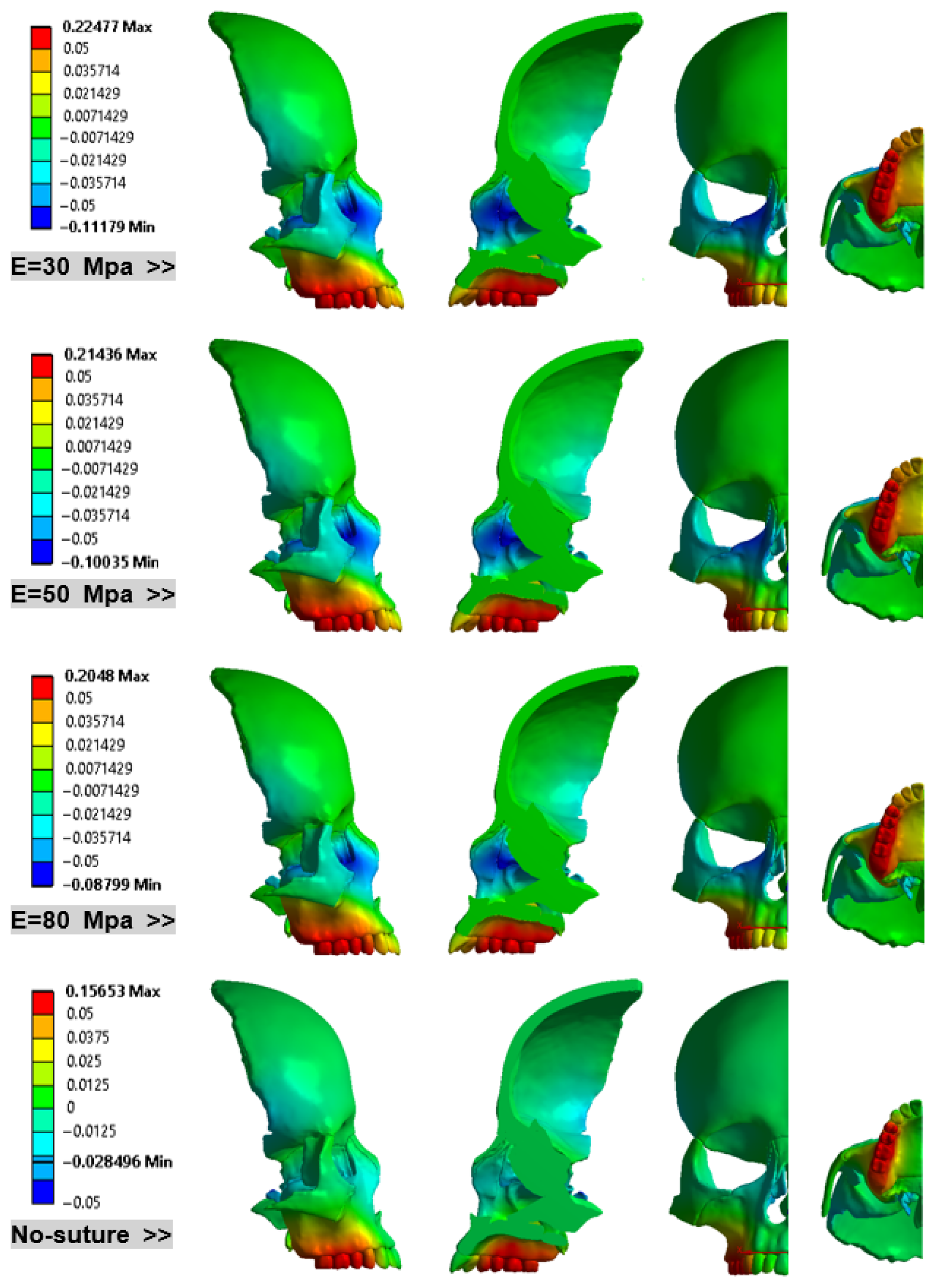
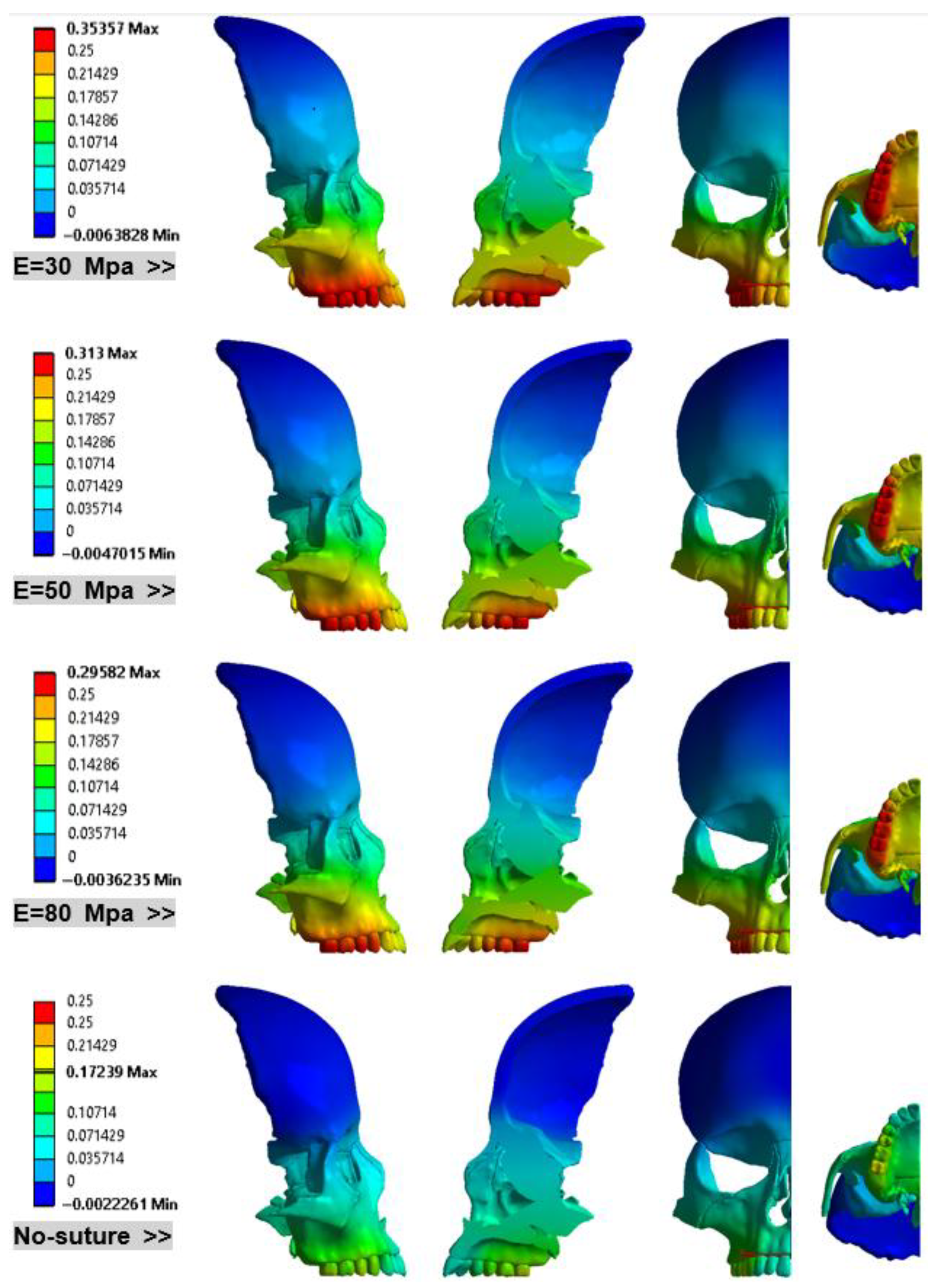
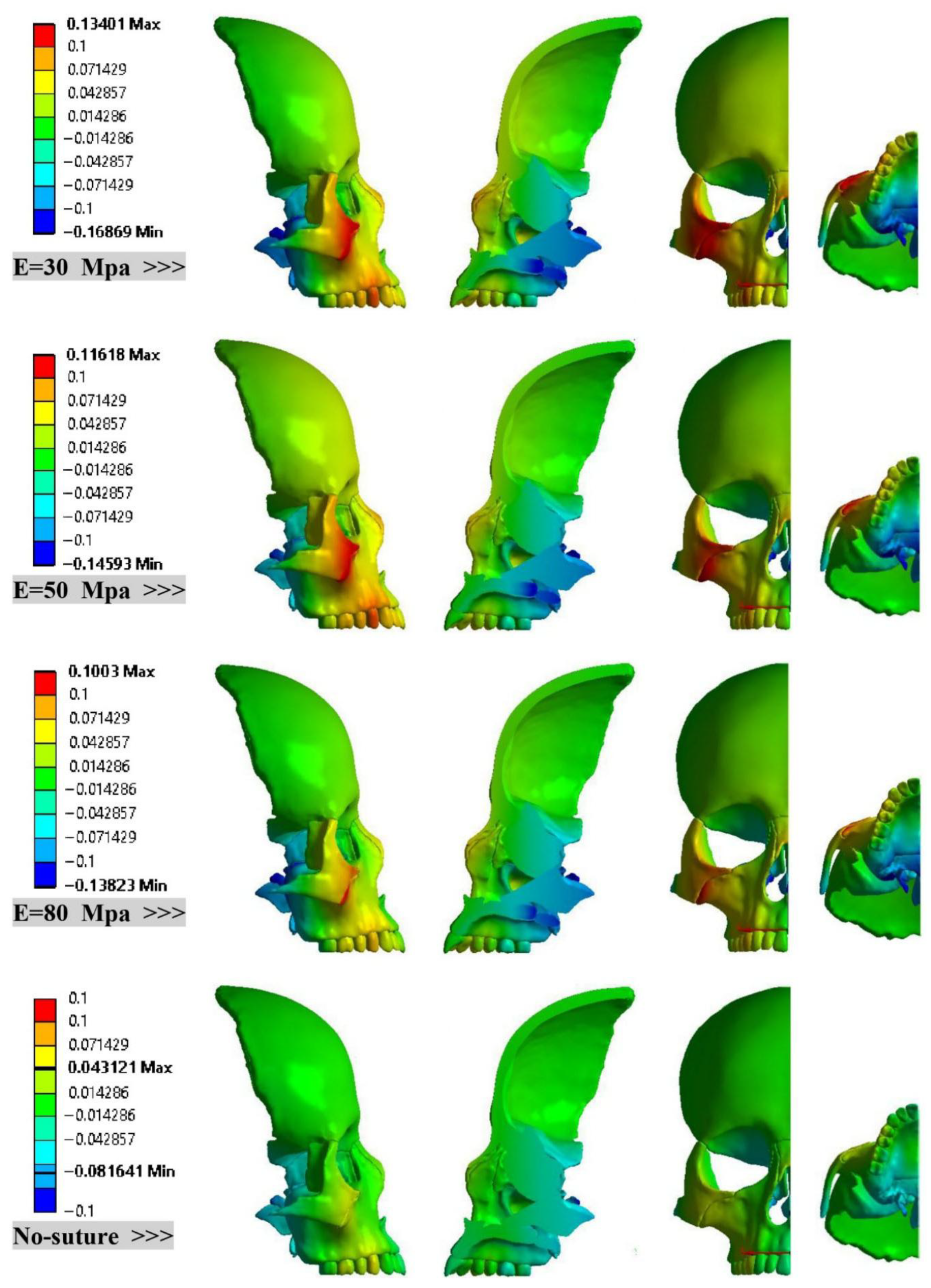
3. Results
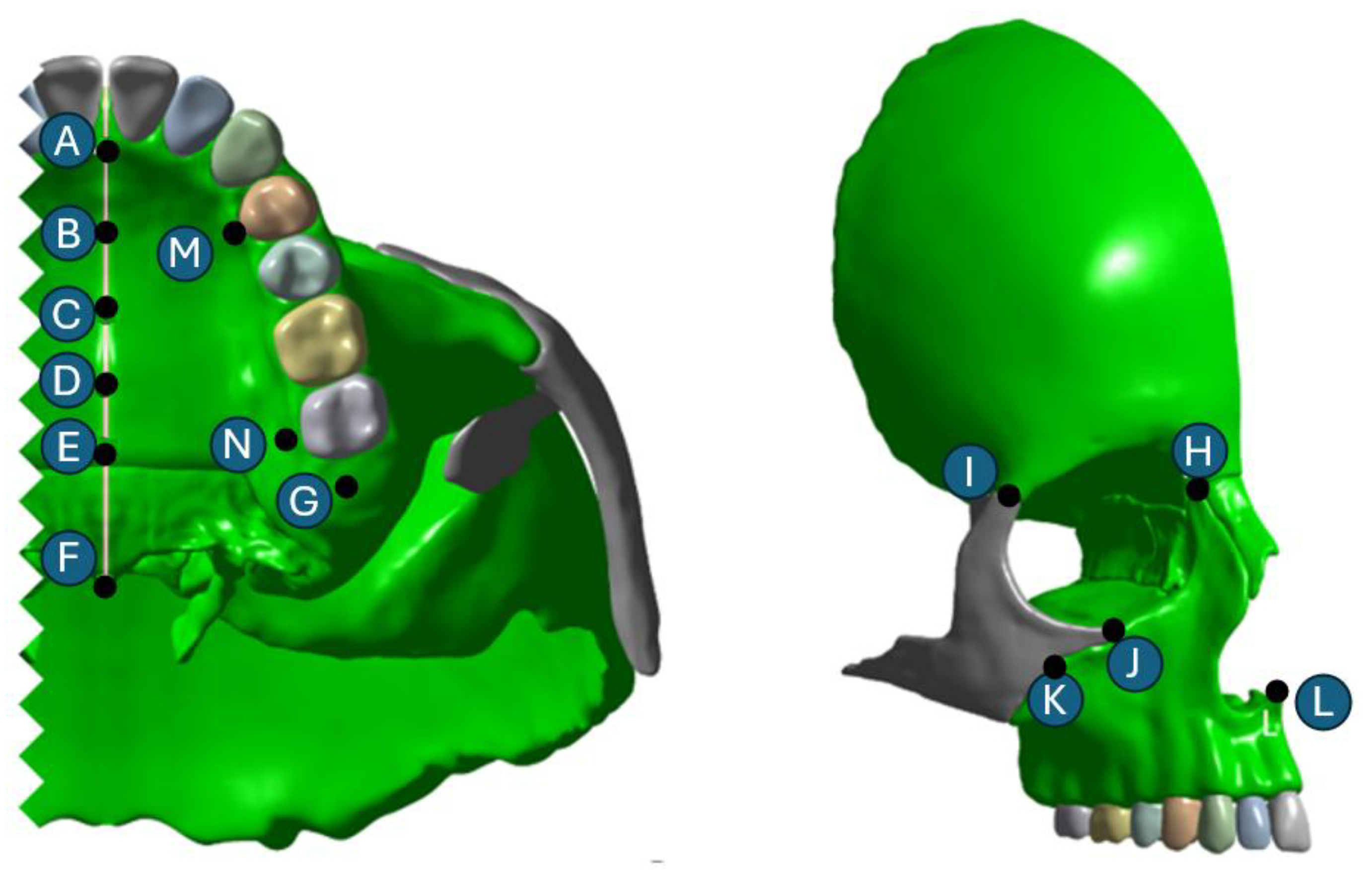
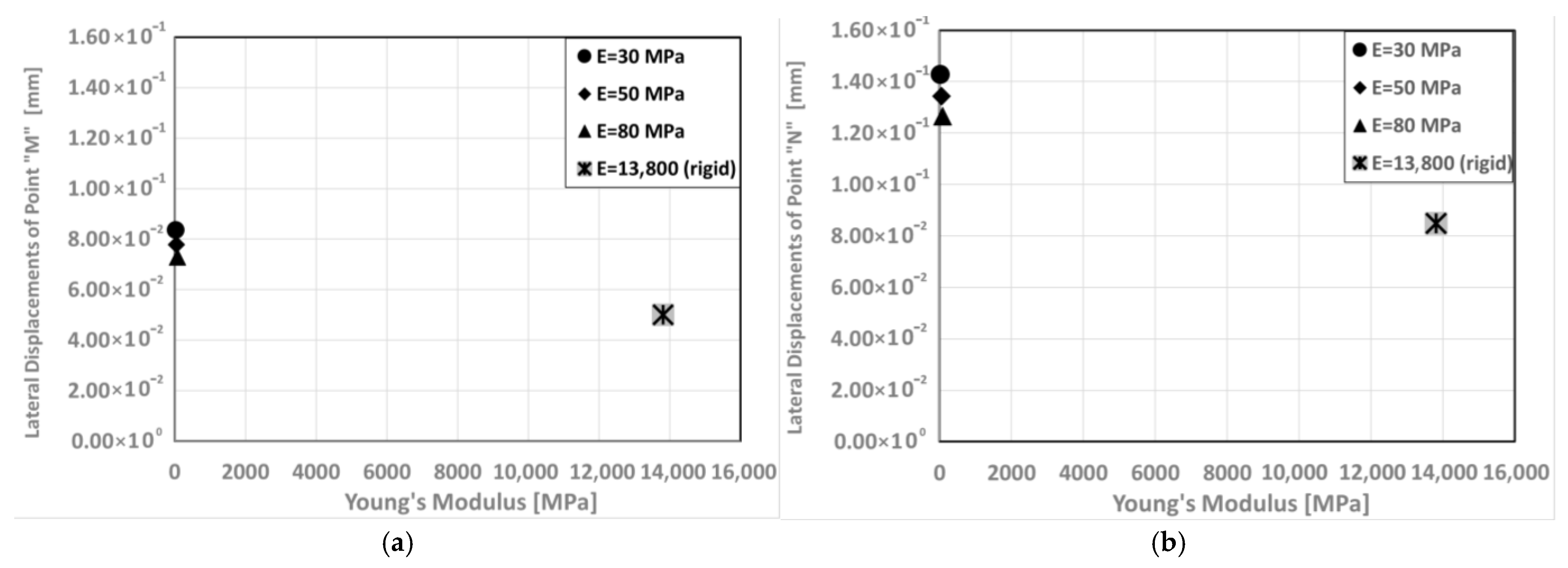
- Lateral Expansion of Maxillary bone: Figure 11 investigates the displacements of point M and N in the lateral direction in models with different Young’s modulus.
- Tabular Summaries of Key Data:
4. Discussion
5. Conclusions
- Maxillary Rotation: Regardless of the suture material properties, RAMPA consistently rotates the maxilla around the X-axis, resulting in an upward rotation.
- Consistent Linear Displacement Slopes: Models incorporating sutures demonstrate consistent linear displacement slopes (approximately 15%) in the X, Y, and Z directions. The locations of minimum and maximum displacements remain unchanged across these sutured models. However, the rigid (no-suture) model predicts significantly different patterns and values for both minimum and maximum displacements.
- Directional Rigidity of the Skull: The skull is mechanically more rigid in the Y direction (anterior) than in the X (lateral) direction. Furthermore, this rigidity increases as suture stiffness increases.
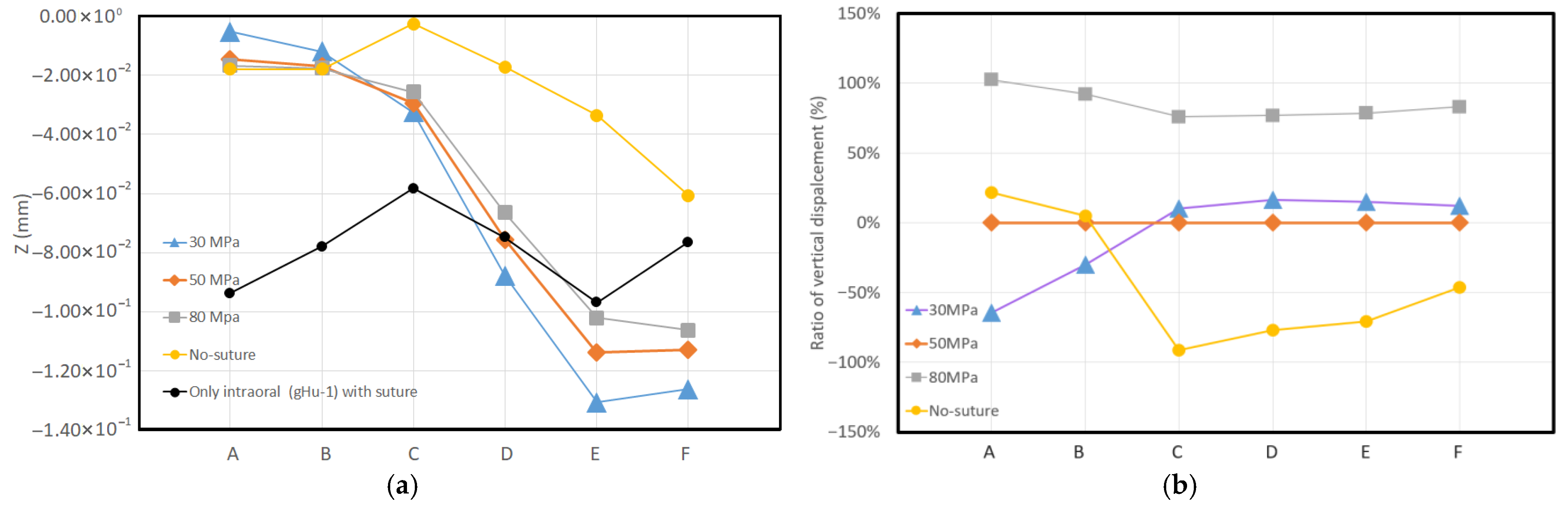
- Mitigation of Downward Displacement: RAMPA significantly mitigates the downward displacements caused by the intraoral device on the midpalatal suture.
- MPS Deformation Patterns: Sutured models treated with RAMPA exhibit a consistent downward displacement trend in the MPS from the front to the back. In sharp contrast, the no-suture (rigid) model shows a completely different deformation pattern.
6. Disclosure
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Romanyk, D.L.; Collins, C.R.; Lagravere, M.O.; Toogood, R.W.; Major, P.W.; Carey, J.P. Role of the midpalatal suture in FEA simulations of maxillary expansion treatment for adolescents: A review. Int. Orthod. 2013, 11, 119–138. [Google Scholar] [CrossRef]
- Moazen, M.; Curtis, N.; O’Higgins, P.; Jones, M.E.H.; Evans, S.E.; Fagan, M.J. Assessment of the role of sutures in a lizard skull: A computer modelling study. Proc. R. Soc. B 2008, 276, 39–46. [Google Scholar] [CrossRef]
- Jasinoski, S.C.; Reddy, B.D. Mechanics of cranial sutures during simulated cyclic loading. J. Biomech. 2012, 45, 2050–2054. [Google Scholar] [CrossRef]
- Popowics, T.E.; Herring, S.W. Load transmission in the nasofrontal suture of the pig, Sus scrofa. J. Biomech. 2007, 40, 837–844. [Google Scholar] [CrossRef]
- Eom, J.; Bayome, M.; Park, J.H.; Lim, H.J.; Kook, Y.A.; Han, S.H. Displacement and stress distribution of the maxillofacial complex during maxillary protraction using palatal plates: A three-dimensional finite element analysis. Korean J. Orthod. 2018, 48, 304–315. [Google Scholar] [CrossRef]
- Jasinoski, S.C.; Reddy, B.D.; Louw, K.K.; Chinsamy, A. Mechanics of cranial sutures using the finite element method. J. Biomech. 2010, 43, 3104–3111. [Google Scholar] [CrossRef] [PubMed]
- Mitani, Y.; Banabilh, S.M.; Singh, G.D. Craniofacial changes in patients with Class III malocclusion treated with the RAMPA system. Int. J. Orthod. Milwaukee 2010, 21, 19–25. [Google Scholar] [PubMed]
- Mitani, Y.; Choi, B.; Choi, J. Anterosuperior protraction of maxillae using the extraoral device, RAMPA; finite element method. Comput. Methods Biomech. Biomed. Eng. 2018, 21, 722–729. [Google Scholar] [CrossRef]
- Moshfeghi, M.; Mitani, Y.; Choi, B.; Emamy, P. Finite element simulations of the effects of an extraoral device, RAMPA, on anterosuperior protraction of maxillae and comparison with gHu-1 intraoral device. ANGEL Orthod. 2021, 91, 804–814. [Google Scholar] [CrossRef] [PubMed]
- Mitani, Y.; Moshfeghi, M.; Kumamoto, N.; Choi, B. Finite element and clinical analyses of effects of a new intraoral device (VomPress) combined with extraoral RAMPA on improving the overjet of craniofacial complex. Comput. Methods Biomech. Biomed. Eng. 2021, 25, 1099–1110. [Google Scholar] [CrossRef]
- Choi, J.W.; Kim, N. Clinical application of three-dimensional printing technology in craniofacial plastic surgery. Arch. Plast. Surg. 2015, 42, 267–277. [Google Scholar] [CrossRef] [PubMed]
- Van Hevele, J.; Nout, E.; Claeys, T.; Meyns, J.; Scheerlinck, J.; Politis, C. Bone-anchored maxillary protraction to correct a class III skeletal relationship: A multicenter retrospective analysis of 218 patients. J. Cranio-Maxillofac. Surg. 2018, 46, 1800–1806. [Google Scholar] [CrossRef]
- Andreucci, C.A.; Fonseca, E.M.M.; Jorge, R.N. Biomechanics of a Novel 3D Mandibular Osteotomy Design. Designs 2024, 8, 57. [Google Scholar] [CrossRef]
- Savoldi, F.; Tsoi, J.; Paganelli, C.; Matinlinna, J.P. Biomechanical behaviour of craniofacial sutures during distraction: An evaluation all over the entire craniofacial skeleton. Dent. Mater. 2017, 33, e290–e300. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Ortiz, C.; Boyce, M.C. Stiffness and strength of suture joints in nature. Phys. Rev. E 2011, 84, 062904. [Google Scholar] [CrossRef]
- Rees, J.S.; Jacobsen, P.H. Elastic modulus of the periodontal ligament. Biomaterials 1997, 18, 995–999. [Google Scholar] [CrossRef]
- Lee, S.C.; Park, J.H.; Bayome, M.; Kim, K.B.; Araujo, E.A.; Kook, Y.A. Effect of bone-borne rapid maxillary expanders with and without surgical assistance on the craniofacial structures using finite element analysis. Am. J. Orthod. Dentofac. Orthop. 2014, 145, 638–648. [Google Scholar] [CrossRef]
- Lillie, E.M.; Urban, J.E.; Weaver, A.A.; Powers, A.K.; Stitzel, J.D. Estimation of skull table thickness with clinical CT and validation with microCT. J. Anat. 2015, 226, 73–80. [Google Scholar] [CrossRef]
- Lillie, E.M.; Urban, J.E.; Lynch, S.K.; Weaver, A.A.; Stitzel, J.D. Evaluation of Skull Cortical Thickness Changes with Age and Sex from Computed Tomography Scans. J. Bone Miner. Res. 2016, 31, 299–307. [Google Scholar] [CrossRef]
- Qian, H.; Chen, J.; Katona, T.R. The influence of PDL principal fibers in a 3-dimensional analysis of orthodontic tooth movement. Am. J. Orthod. Dentofac. Orthop. 2001, 120, 272–279. [Google Scholar] [CrossRef]
- Cattaneo, P.M.; Dalstra, M.; Melsen, B. The finite element method: A tool to study orthodontic tooth movement. J. Dent. Res. 2005, 84, 428–433. [Google Scholar] [CrossRef]
- Fricke-Zech, S.; Gruber, R.M.; Dullin, C.; Zapf, A.; Kramer, F.J.; Kubein-Meesenburg, D.; Hahn, W. Measurement of the midpalatal suture width. Angle Orthod. 2012, 82, 145–150. [Google Scholar] [CrossRef] [PubMed]
- Fill, T.S.; Toogood, R.W.; Major, P.W.; Carey, J.P. Analytically determined mechanical properties of, and models for the periodontal ligament: Critical review of literature. J. Biomech. 2012, 45, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Serpe, L.C.T.; Las Casas, E.B.; Toyofuku, A.C.M.M.; González-Torres, L.A. A bilinear elastic constitutive model applied for midpalatal suture behavior during rapid maxillary expansion. Res. Biomed. Eng. 2015, 31, 319–327. [Google Scholar] [CrossRef][Green Version]
- Lee, H.; Ting, K.; Nelson, M.; Sun, N.; Sung, S.J. Maxillary expansion in customized finite element method models. Am. J. Orthod. Dentofac. Orthop. 2009, 136, 367–374. [Google Scholar] [CrossRef]




| Item | Young’s Modulus [MPa] | Poisson’s Ratio |
|---|---|---|
| Cortical bone | 13,800 MPa | 0.26 |
| Cancellous bone | 1370 MPa | 0.3 |
| Stainless steel (AISI 316) | 193,000 MPa | 0.31 |
| Teeth | 18,600 MPa | 0.31 |
| Periodontal ligament | 50 MPa | 0.49 |
| Midpalatal suture (MPS) | 50 MPa | 50 |
| Acrylic Resin (Orthocryl® from DENTAURUM, Ispringen, Germany) | 3543 MPa | 0.3 |
| Sutures | 30 MPa (Case 1) | - |
| 50 MPa (Case 2) | 0.49 | |
| 80 MPa (Case 3) | 0.49 | |
| 13,800 MPa (rigid; Case 4) | 0.49 |
| X Direction | Y Direction | Z Direction | |
|---|---|---|---|
| Variation in maximum ratio | 69.6%~76.1% | 34.9%~61.1% | 32.1–43.1% |
| Variation in minimum ratio | 25.1%~31.8% | 48.7%~58.1% | 49.0–59% |
| Point | Case 1 (30 MPa) | Case 2 (50 MPa) | Case 3 (80 MPa) | Case 4 (No-Suture) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X [mm] | Y [mm] | Z [mm] | X [mm] | Y [mm] | Z [mm] | X [mm] | Y [mm] | Z [mm] | X [mm] | Y [mm] | Z [mm] | |
| A | 3.155 × 10 −2 | 0.195 | −5.228 × 10 −3 | 2.590 × 10 −2 | 0.163 | −1.470 × 10 −2 | 2.141 × 10 −2 | 0.152 | −1.670 × 10 −2 | 1.96 × 10 −3 | 7.2728 × 10 −2 | −1.785 × 10 −2 |
| B | 2.215 × 10 −2 | 0.195 | −1.189 × 10 −2 | 1.853 × 10 −2 | 0.168 | −1.704 × 10 −2 | 1.521 × 10 −2 | 0.159 | −1.761 × 10 −2 | 1.233 × 10 −3 | 8.496 × 10 −2 | −1.786 × 10 −2 |
| C | 2.714 × 10 −2 | 0.207 | −3.244 × 10 −2 | 2.283 × 10 −2 | 0.181 | −2.945 × 10 −2 | 1.95 × 10 −2 | 0.172 | −2.564 × 10 −2 | 2.655 × 10 −3 | 9.727 × 10 −2 | −2.516 × 10 −3 |
| D | 3.546 × 10 −2 | 0.225 | −8.773 × 10 −2 | 2.868 × 10 −2 | 0.197 | −7.551 × 10 −2 | 2.355 × 10 −2 | 0.187 | −6.640 × 10 −2 | 1.936 × 10 −3 | 0.109 | −1.723 × 10 −2 |
| E | 4.107 × 10 −2 | 0.228 | −0.131 | 3.342 × 10 −2 | 0.200 | −0.114 | 2.759 × 10 −2 | 0.190 | −0.102 | 1.624 × 10 −3 | 0.112 | −3.348 × 10 −2 |
| F | −8.089 × 10 −2 | 0.238 | −0.126 | −1.432 × 10 −4 | 0.209 | −0.113 | −1.822 × 10 −4 | 0.200 | −0.106 | 5.904e−6 | 0.122 | −6.072 × 10 −2 |
| Point | Case 1 (30 MPa) | Case 2 (50 MPa) | Case 3 (80 MPa) | Case 4 (No-Suture) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X [mm] | Y [mm] | Z [mm] | X [mm] | Y [mm] | Z [mm] | X [mm] | Y [mm] | Z [mm] | X [mm] | Y [mm] | Z [mm] | |
| G | 0.154 | 0.308 | −0.059 | 0.144 | 0.271 | −0.05 | 0.134 | 0.256 | −0.055 | 0.076 | 0.143 | −0.034 |
| H | 0.002 | 0.076 | 0.026 | 0.002 | 0.065 | 0.018 | 0.002 | 0.060 | 0.012 | 0.001 | 0.035 | 0.000 |
| I | 0.000 | 0.045 | 0.030 | 0.001 | 0.034 | 0.023 | 0.001 | 0.028 | 0.019 | 0.005 | 0.014 | 0.012 |
| J | −0.041 | 0.121 | 0.109 | −0.036 | 0.107 | 0.093 | −0.029 | 0.104 | 0.079 | −0.004 | 0.067 | 0.027 |
| K | −0.027 | 0.169 | 0.115 | −0.025 | 0.150 | 0.101 | −0.020 | 0.143 | 0.089 | 0.002 | 0.077 | 0.036 |
| L | −0.005 | 0.173 | 0.019 | −0.003 | 0.153 | 0.009 | −0.002 | 0.147 | 0.005 | 0.000 | 0.092 | −0.012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moshfeghi, M.; Mitani, Y.; Okai-Kojima, Y.; Choi, B.; Emamy, P. RAMPA Therapy: Impact of Suture Stiffness on the Anterosuperior Protraction of Maxillae; Finite Element Analysis. Oral 2025, 5, 74. https://doi.org/10.3390/oral5040074
Moshfeghi M, Mitani Y, Okai-Kojima Y, Choi B, Emamy P. RAMPA Therapy: Impact of Suture Stiffness on the Anterosuperior Protraction of Maxillae; Finite Element Analysis. Oral. 2025; 5(4):74. https://doi.org/10.3390/oral5040074
Chicago/Turabian StyleMoshfeghi, Mohammad, Yasushi Mitani, Yuko Okai-Kojima, Bumkyoo Choi, and Peiman Emamy. 2025. "RAMPA Therapy: Impact of Suture Stiffness on the Anterosuperior Protraction of Maxillae; Finite Element Analysis" Oral 5, no. 4: 74. https://doi.org/10.3390/oral5040074
APA StyleMoshfeghi, M., Mitani, Y., Okai-Kojima, Y., Choi, B., & Emamy, P. (2025). RAMPA Therapy: Impact of Suture Stiffness on the Anterosuperior Protraction of Maxillae; Finite Element Analysis. Oral, 5(4), 74. https://doi.org/10.3390/oral5040074






