X-Ray Interaction and the Electronic, Atomic Cross-Sections and Compton Mass-Attenuation Coefficients of Human Blood, Breasts, Eye Lens, Ovaries, and Testis
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
3. Effective Z and Effective A of Tissues
4. Results
4.1. Radiation Energy and Tissue Effective Charge Number
4.2. Radiation Energy and Klein–Nishina Electronic and Atomic Cross-Sections
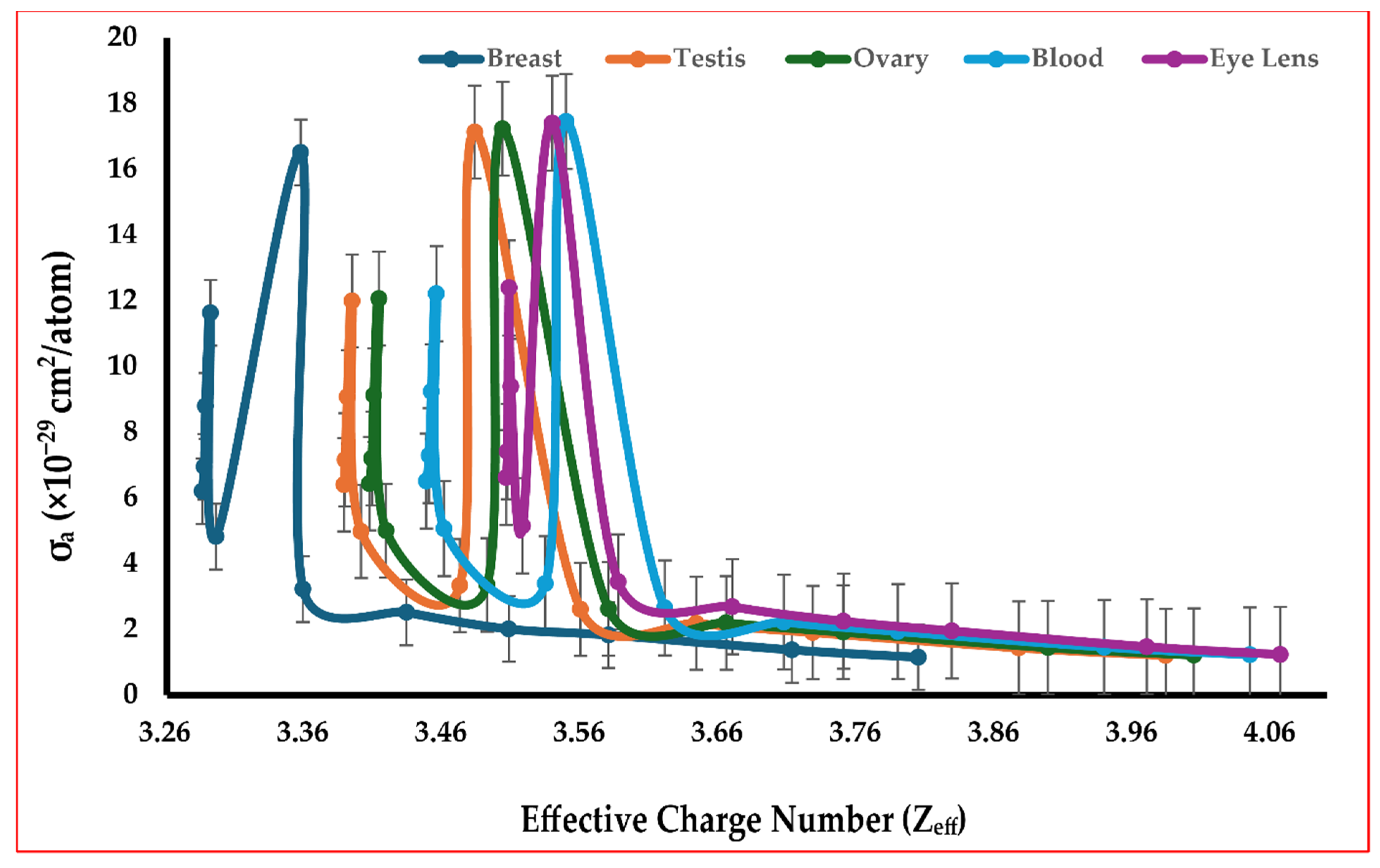
4.3. Tissue Effective Charge Number Zeff and Klein–Nishina Atomic Cross-Section
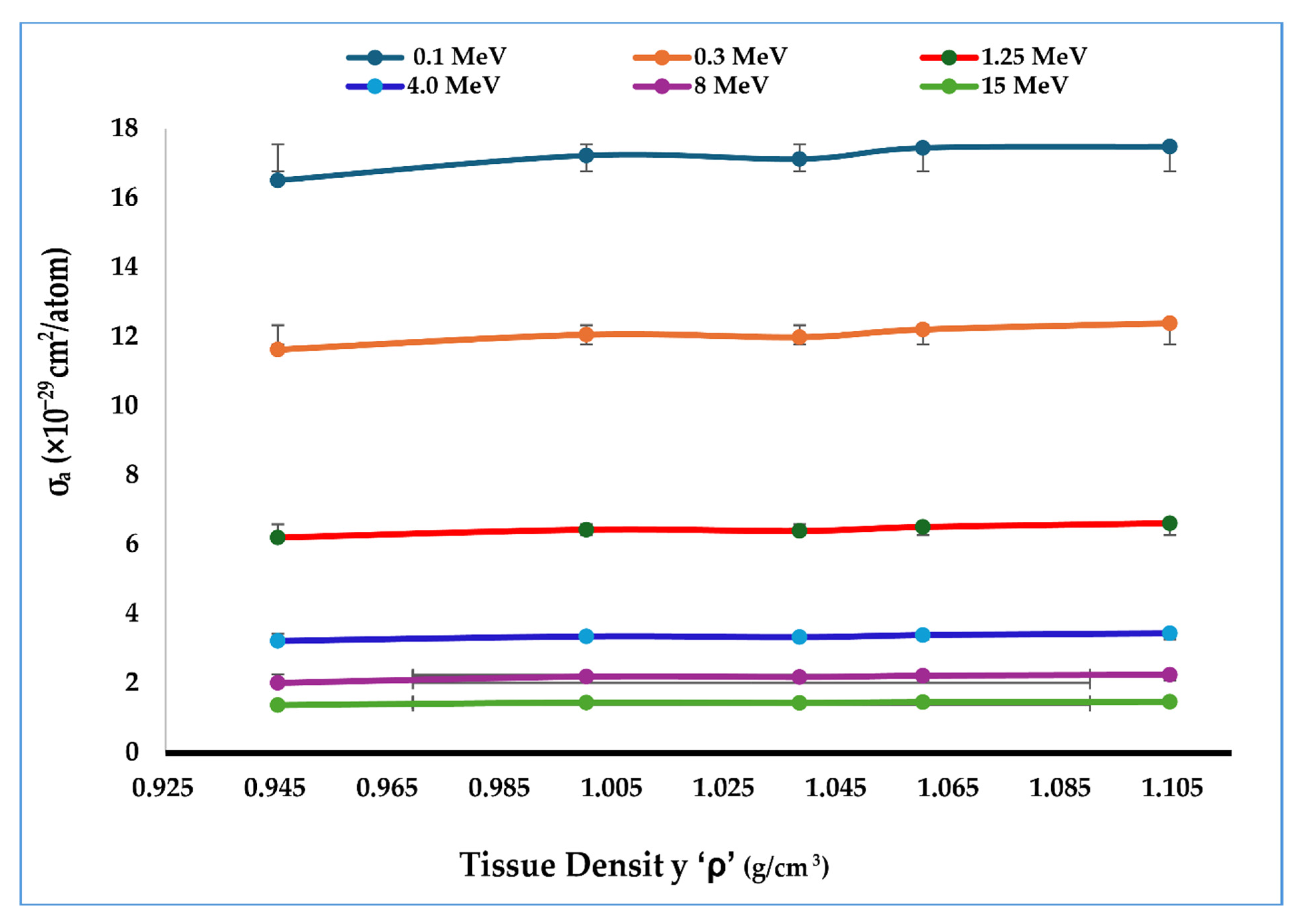
4.4. Tissue Density and Klein–Nishina Atomic Cross-Section
4.5. Tissue Electron Density ρe and Klein–Nishina Atomic Cross-Section
4.6. Compton Mass-Attenuation Coefficient σ/ρ
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pereira, G.C.; Traughber, M.; Muzic, R., Jr. The Role of Imaging in Radiation Therapy Planning: Past, Present, and Future. BioMed Res. Int. 2014, 2014, 231090. [Google Scholar] [CrossRef]
- Fatima, Z.; Ali, N.; Williams, M.; Dhar, S.; Maqbool, M. X-ray scattering and attenuation cross-sections and coefficients of bone, brain, lung, fat, and soft tissue for applications in dosimetry, cancer detection, and treatment. Radiat. Phys. Chem. 2023, 208, 110908. [Google Scholar] [CrossRef]
- Huh, H.D.; Kim, S. History of radiation therapy technology. Prog. Med. Phys. 2020, 31, 124–134. [Google Scholar] [CrossRef]
- Baskar, R.; Lee, K.; Yeo, R.; Yeoh, K.W. Cancer and Radiation Therapy: Current Advances and Future Directions. Int. J. Med. Sci. 2012, 9, 193–199. [Google Scholar] [CrossRef]
- Okunieff, P.; Morgan, D.; Niemierko, A.; Suit, H.D. Radiation Dose-Response of Human Tumors. Int. J. Radiat. Oncol. Biol. Phys. 1995, 32, 1227–1237. [Google Scholar] [CrossRef]
- Breitkreutz, D.; Weil, M.; Bazalova-Carter, M. External beam radiation therapy with kilovoltage x-rays. Phys. Medica 2020, 79, 103–112. [Google Scholar] [CrossRef]
- Fisher, D.R. Radiation Dosimetry for Radioimmunotherapy. An Overview of Current Capabilities and Limitations. Cancer 1994, 73 (Suppl. S3), 905–911. [Google Scholar] [CrossRef] [PubMed]
- Hellevik, T.; Martinez-Zubiaurre, I. Radiotherapy and the Tumor Stroma: The Importance of Dose and Fractionation. Front. Oncol. 2014, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Desrosiers, M.; DeWerd, L.; Deye, J.; Lindsay, P.; Murphy, M.K.; Mitch, M.; Macchiarini, F.; Stojadinovic, S.; Stone, H. The Importance of Dosimetry Standardization in Radiobiology. J. Res. Natl. Inst. Stand. Technol. 2013, 118, 403–418. [Google Scholar] [CrossRef] [PubMed]
- Alenezi, M.; Stinson, K.; Maqbool, M.; Bolus, N. Klein-Nishina electronic cross-section, Compton cross sections, and buildup factor of wax, for radiation shielding and protection. J. Radiol. Prot. 2018, 38, 372–381. [Google Scholar] [CrossRef]
- Pratt, R. Photon absorption and photon scattering—What we do not know and why it matters. Radiat. Phys. Chem. 2014, 95, 4–13. [Google Scholar] [CrossRef]
- Massillon-JL, G. Future directions on low-energy radiation dosimetry. Sci. Rep. 2021, 11, 10569. [Google Scholar] [CrossRef] [PubMed]
- Ming, C.; Ma, C.; Chetty, I.; Deng, J.; Faddegon, B.; Jiang, S.; Li, J.; Seuntjens, J.; Siebers, J.; Traneus, E. Beam modeling and beam model commissioning for Monte Carlo dose calculation-based radiation therapy treatment planning: Report of AAPM Task Group 157. Med. Phys. 2020, 47, e1–e18. [Google Scholar]
- Deloch, L.; Derer, A.; Hartmann, J.; Frey, B.; Fietkau, R.; Gaipl, U.S. Modern Radiotherapy Concepts and the Impact of Radiation on Immune Activation. Front. Oncol. 2016, 6, 141. [Google Scholar] [CrossRef]
- Donya, M.; Radford, M.; Elguindy, A.; Firmin, E.; Yacoub, M.H. Radiation in medicine: Origins, risks, and aspirations. Glob. Cardiol. Sci. Pract. 2014, 2014, 57. [Google Scholar] [CrossRef]
- Barnett, G.C.; West, C.M.L.; Dunning, A.M.; Elliott, R.M.; Coles, C.E.; Pharoah, P.D.P.; Burnet, N.G. Normal tissue reactions to radiotherapy: Towards tailoring treatment dose by genotype. Nat. Rev. Cancer 2009, 9, 134–142. [Google Scholar] [CrossRef] [PubMed]
- Stone, H.B.; Coleman, C.N.; Anscher, M.S.; McBride, W.H. Effects of radiation on normal tissue: Consequences and mechanisms. Lancet Oncol. 2003, 4, 529–536. [Google Scholar] [CrossRef] [PubMed]
- Attix, F.H. Introduction to Radiological Physics and Radiation Dosimetry; Wiley: New York, NY, USA, 2004; pp. 124–157. [Google Scholar]
- Maqbool, M. An Introduction to Medical Physics; Springer: New York, NY, USA, 2017; pp. 43–67. [Google Scholar]
- Ottolenghi, A.; Smyth, V.; Trott, K.R. The risks to healthy tissues from the use of existing and emerging techniques for radiation therapy. Radiat. Prot. Dosim. 2011, 143, 533–535. [Google Scholar] [CrossRef]
- Lapierre, A.; Bourillon, L.; Larroque, M.; Gouveia, T.; Bourgier, C.; Mahmut Ozsahin, M.; Pèlegrin, A.; Azria, D.; Brengues, M. Improving Patients’ Life Quality after Radiotherapy Treatment by Predicting Late Toxicities. Cancers 2022, 14, 2097. [Google Scholar] [CrossRef]
- Cleland, M.R.; Stichelbaut, F. Radiation processing with high-energy X-rays. Radiat. Phys. Chem. 2013, 84, 91–99. [Google Scholar] [CrossRef]
- Momose, A. X-ray phase imaging reaching clinical uses. Phys. Medica 2020, 79, 93–102. [Google Scholar] [CrossRef] [PubMed]
- Ha, D.; Lee, S.; Ghergherehchi, M.; Choi, H.; Namgoong, H.; Lee, J.; Chai, J. 6 MV X-band linear accelerator for stereotactic body radiation therapy. Nucl. Eng. Technol. 2024, 56, 4502–4511. [Google Scholar] [CrossRef]
- Esien-Umo, E.; Obu, J.; Chiaghanam, N.; Ugbem, T.; Egbe, N. Photon interaction coefficients for the colorectal cancer tissue. J. Med. Phys. 2023, 47, 381–386. [Google Scholar] [CrossRef]
- Alexander, R.; Thiele, K.; Maqbool, M. Electronic cross-sections and Compton attenuation and transfer coefficients of 82Pb208, 29Cu64, 27Co59, 20Ca40, and 13Al27 for applications in radiation shielding and dosimetry. Phys. Scr. 2020, 95, 085006. [Google Scholar] [CrossRef]
- Kurudirek, M. Effective atomic numbers and electron densities of some human tissues and dosimetric materials for mean energies of various radiation sources relevant to radiotherapy and medical applications. Radiat. Phys. Chem. 2014, 102, 139–146. [Google Scholar] [CrossRef]
- Jayachandran, C. Calculated effective atomic number and kerma values for tissue-equivalent and dosimetry materials. Phys. Med. Biol. 1971, 16, 617–623. [Google Scholar] [CrossRef]
- Perrigin, M.; Williams, K.; Wright, B.; Maqbool, M.; Caffrey, E.; George, R.; Ali, G.; Maqbool, M. Low melting point MCP-69, MCP-96, MCP-137, and MCP-200 alloys for radiation protection in radiological and therapeutic processes. Radiat. Med. Prot. 2022, 3, 175–182. [Google Scholar] [CrossRef]
- De Souza, A.; Aristone, F.; Gouvea, A.; Fernandes, H. Characterization and measurement of gamma radiation shielding of a new tungsten-lignin composite. J. Compos. Mater. 2021, 55, 3579–3588. [Google Scholar] [CrossRef]
- Pons, D.; Pons, A.; Pons, A. Nuclear polymer explains the stability, instability, and nonexistence of nuclides. Physiother. Res. Int. 2015, 2015, 651361. [Google Scholar] [CrossRef]
- Salehi, D.; Sardari, D.; Jozani, M. Investigation of some radiation shielding parameters in soft tissue. J. Radiat. Res. Appl. Sci. 2015, 8, 439–445. [Google Scholar] [CrossRef]
- Kalyani, I.; Altowyan, A.; Edukondalu, A.; Pujari, N.; Reddy, M.; Alrowaili, Z.; Olarinoye, I.; Al-Buriahi, M. Synthesis, Thermal, Optical, and Radiation-Absorbing Properties of Bi2O3-Li2O-As2O3-B2O3 Glasses. J. Electron. Mater. 2023, 52, 569–582. [Google Scholar] [CrossRef]

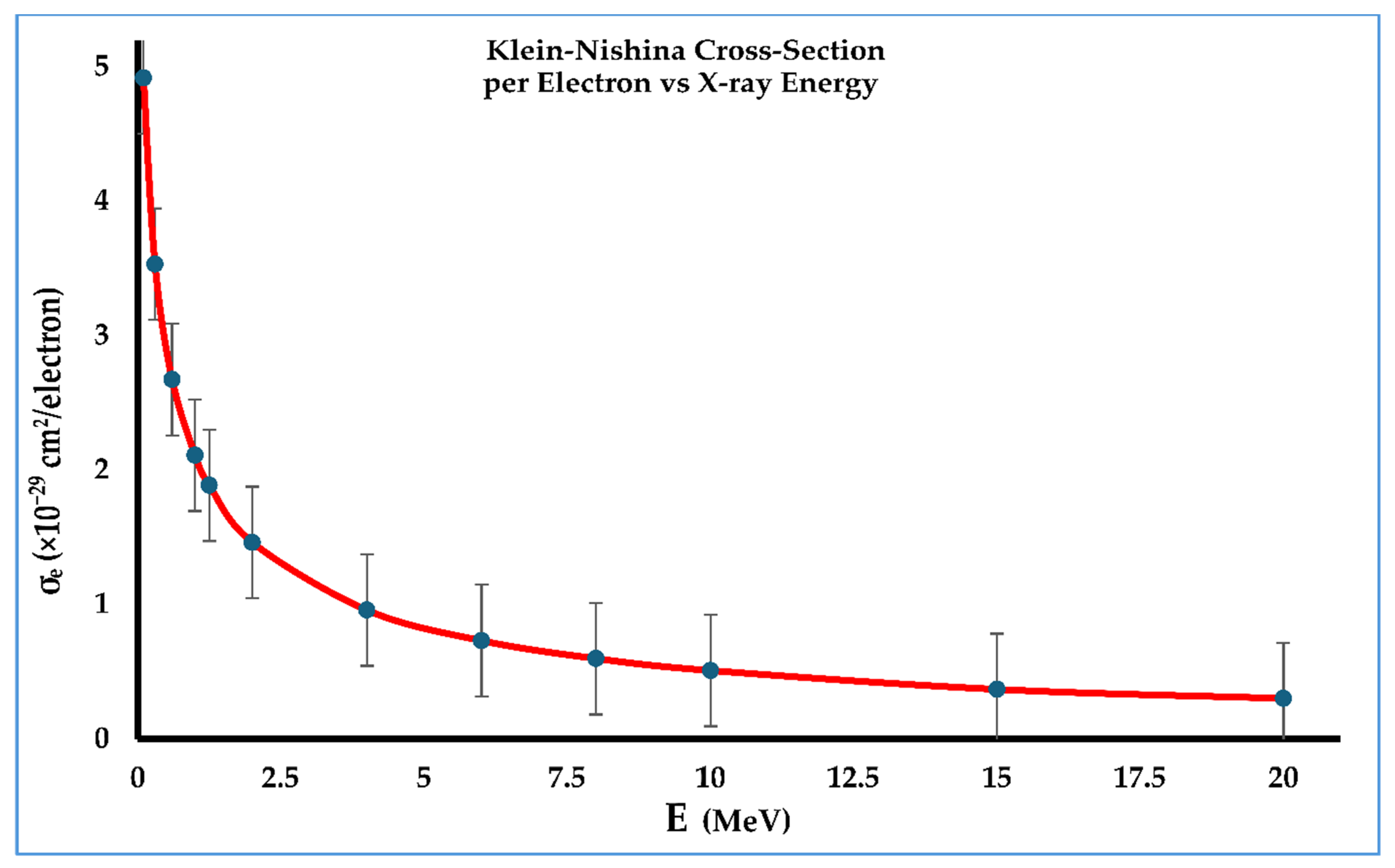



| Energy (MeV) | Coupling Constant α | Klein–Nishina Cross-Section per Electron σe (cm2/Electron) |
|---|---|---|
| 0.1 | 0.19569 | 4.918 |
| 0.3 | 0.58708 | 3.533 |
| 0.6 | 1.1742 | 2.675 |
| 1.0 | 1.9569 | 2.112 |
| 1.25 | 2.4462 | 1.888 |
| 2.0 | 3.9139 | 1.463 |
| 4.0 | 7.8278 | 0.9596 |
| 6.0 | 11.742 | 0.7323 |
| 8.0 | 15.656 | 0.5987 |
| 10.0 | 19.569 | 0.5098 |
| 15.0 | 29.354 | 0.3696 |
| 20.0 | 39.139 | 0.3024 |
| Energy (MeV) | Zeff | σa (×10−29 cm−2) (Breast) |
|---|---|---|
| 0.1 | 3.2856 | 16.51 |
| 0.3 | 3.287 | 11.63 |
| 0.6 | 3.2879 | 8.795 |
| 1.0 | 3.2916 | 6.942 |
| 1.25 | 3.2956 | 6.203 |
| 2.0 | 3.3568 | 4.821 |
| 4.0 | 3.3585 | 3.223 |
| 6.0 | 3.4335 | 2.514 |
| 8.0 | 3.5075 | 2.01 |
| 10.0 | 3.5797 | 1.825 |
| 15.0 | 3.7125 | 1.372 |
| 20.0 | 3.804 | 1.15 |
| Energy (MeV) | Zeff | σa (×10−29 cm−2) (Testis) |
|---|---|---|
| 0.1 | 3.3882 | 17.13 |
| 0.3 | 3.389 | 11.99 |
| 0.6 | 3.3906 | 9.07 |
| 1.0 | 3.3941 | 7.158 |
| 1.25 | 3.4005 | 6.397 |
| 2.0 | 3.472 | 4.975 |
| 4.0 | 3.4829 | 3.332 |
| 6.0 | 3.5594 | 2.607 |
| 8.0 | 3.6432 | 2.181 |
| 10.0 | 3.7276 | 1.9 |
| 15.0 | 3.8767 | 1.433 |
| 20.0 | 3.9831 | 1.204 |
| Energy (MeV) | Zeff | σa (×10−29 cm−2) (Ovary) |
|---|---|---|
| 0.1 | 3.4067 | 17.23 |
| 0.3 | 3.4084 | 12.06 |
| 0.6 | 3.4098 | 9.121 |
| 1.0 | 3.4135 | 7.199 |
| 1.25 | 3.4187 | 6.432 |
| 2.0 | 3.4918 | 5.002 |
| 4.0 | 3.503 | 3.351 |
| 6.0 | 3.5797 | 2.621 |
| 8.0 | 3.6649 | 2.194 |
| 10.0 | 3.7496 | 1.912 |
| 15.0 | 3.8979 | 1.441 |
| 20.0 | 4.0034 | 1.211 |
| Energy (MeV) | Zeff | σa (×10−29 cm−2) (Blood) |
|---|---|---|
| 0.1 | 3.4479 | 17.45 |
| 0.3 | 3.4499 | 12.21 |
| 0.6 | 3.4514 | 9.232 |
| 1.0 | 3.4551 | 7.286 |
| 1.25 | 3.4607 | 6.51 |
| 2.0 | 3.534 | 5.063 |
| 4.0 | 3.549 | 3.391 |
| 6.0 | 3.6204 | 2.651 |
| 8.0 | 3.7067 | 2.219 |
| 10.0 | 3.7892 | 1.932 |
| 15.0 | 3.9385 | 1.456 |
| 20.0 | 4.044 | 1.223 |
| Energy (MeV) | Zeff | σa (×10−29 cm−2) (Eye Lens) |
|---|---|---|
| 0.1 | 3.5056 | 17.4 |
| 0.3 | 3.5065 | 12.39 |
| 0.6 | 3.5077 | 9.387 |
| 1.0 | 3.5091 | 7.406 |
| 1.25 | 3.5175 | 6.619 |
| 2.0 | 3.539 | 5.146 |
| 4.0 | 3.5868 | 3.442 |
| 6.0 | 3.6693 | 2.687 |
| 8.0 | 3.7498 | 2.245 |
| 10.0 | 3.8282 | 1.952 |
| 15.0 | 3.9693 | 1.467 |
| 20.0 | 4.066 | 1.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banks, D.; Kapshtica, E.; Ali, J.; Raja, S.; Raja, M.; Ali, M.; Maqbool, M. X-Ray Interaction and the Electronic, Atomic Cross-Sections and Compton Mass-Attenuation Coefficients of Human Blood, Breasts, Eye Lens, Ovaries, and Testis. Radiation 2025, 5, 24. https://doi.org/10.3390/radiation5030024
Banks D, Kapshtica E, Ali J, Raja S, Raja M, Ali M, Maqbool M. X-Ray Interaction and the Electronic, Atomic Cross-Sections and Compton Mass-Attenuation Coefficients of Human Blood, Breasts, Eye Lens, Ovaries, and Testis. Radiation. 2025; 5(3):24. https://doi.org/10.3390/radiation5030024
Chicago/Turabian StyleBanks, Daniel, Elise Kapshtica, Jia Ali, Sami Raja, Madhesh Raja, Mishka Ali, and Muhammad Maqbool. 2025. "X-Ray Interaction and the Electronic, Atomic Cross-Sections and Compton Mass-Attenuation Coefficients of Human Blood, Breasts, Eye Lens, Ovaries, and Testis" Radiation 5, no. 3: 24. https://doi.org/10.3390/radiation5030024
APA StyleBanks, D., Kapshtica, E., Ali, J., Raja, S., Raja, M., Ali, M., & Maqbool, M. (2025). X-Ray Interaction and the Electronic, Atomic Cross-Sections and Compton Mass-Attenuation Coefficients of Human Blood, Breasts, Eye Lens, Ovaries, and Testis. Radiation, 5(3), 24. https://doi.org/10.3390/radiation5030024







