Energy Efficiency Enhancement in Pressurized Irrigation Networks through Optimal Location of Pumps-as-Turbines: A Case Study in Spain ^†

Abstract

One of the hardest challenges in irrigation systems is to reduce the use of water resources. The goal “more crop per drop“ has fostered the improvement of hydraulic infrastructure by replacing old open channel networks with pressurized systems (e.g., drip and sprinkler irrigation). This has resulted in reduced water losses, as well as the possibility for farmers to benefit from on-demand water. On the other hand, this improvement in water efficiency has controversially resulted in a large increase in energy consumption, since pressurized systems demand large flows with high pressures. The high energy requirements, along with the investment and operational costs, may compromise the viability of such irrigation systems. Several strategies to save both water and energy resources have, therefore, been proposed in the recent literature. Among these, the exploitation of excess pressure to produce energy by means of energy production devices (EPDs) has been proven to be a very effective strategy. Pumps-as-turbines (PATs) are, by far, preferred over traditional EPDs, such as pico- or micro-turbines, being very cost-effective solutions. In this study, the optimal location of PATs within an irrigation system is investigated with reference to a whole irrigation season. A case study network, the Zújar Canal irrigation district, is considered, for which accurate records of hourly water demands are available due to a diffuse telemetry system over the irrigation area. The aim of the optimization is to search for the best number and location of PATs within the irrigation network in order to maximize the energy production and minimize the investment costs. The hydraulic resolution of the network is coupled with the optimal location problem in one single mathematical model and the optimization procedure is performed via the use of a global optimization solver. The promising results in terms of the hydropower potential prove the effectiveness of the PAT installation within the case study network.

1. Introduction

“On-demand” pressurized networks in irrigation districts are vast hydraulic structures, which are very demanding in terms of their energy requirements [1,2] and distribute large flows at high pressures [3]. The layout of such a structure covers an extensive surface area, usually thousands of hectares, and consists of tens or hundreds of kilometers of pipes [4]. Hydro energy recovery from irrigation networks through the implementation of pumps-as-turbines (PATs) is a topic that has deeply investigated in the recent literature [5,6]. PATs are cost-effective solutions for green electricity generation in those points of the network characterized by pressures greater than the required service value [7,8,9,10]. In a recent study at real scale in Southern Spain, a 4 kW PAT replaced an existing diesel generator that supplied electricity for the irrigation practice at a farm [11]. However, the optimal and automatic location of such energy recovery devices within irrigation networks has not been addressed in detail. Therefore, the potential of this technology should be explored throughout this infrastructure, either for self-consumption within the community or even for injection into the grid [12]. A detailed study of possible optimal sites or locations is necessary [13,14], considering the entire hydraulic network and evaluating different optimization criteria. Once the possible locations are identified, it is essential to correctly select [15,16,17] a turbomachine by studying in detail the variations in terms of flow rates and pressures, as well as the characteristic curves of the devices.

In this study, a global optimization solver is used to search for the optimal number and location of PATs within a real irrigation network, with the aim of maximizing the energy savings and minimizing the investment costs. The hydraulic behavior of the network is simulated along with the optimization procedure within one single mathematical model. The robustness of the performed procedure is proved by the analysis of the solution quality, which is possible when the optimization procedure is undertaken using global optimization solvers.

2. The Case Study

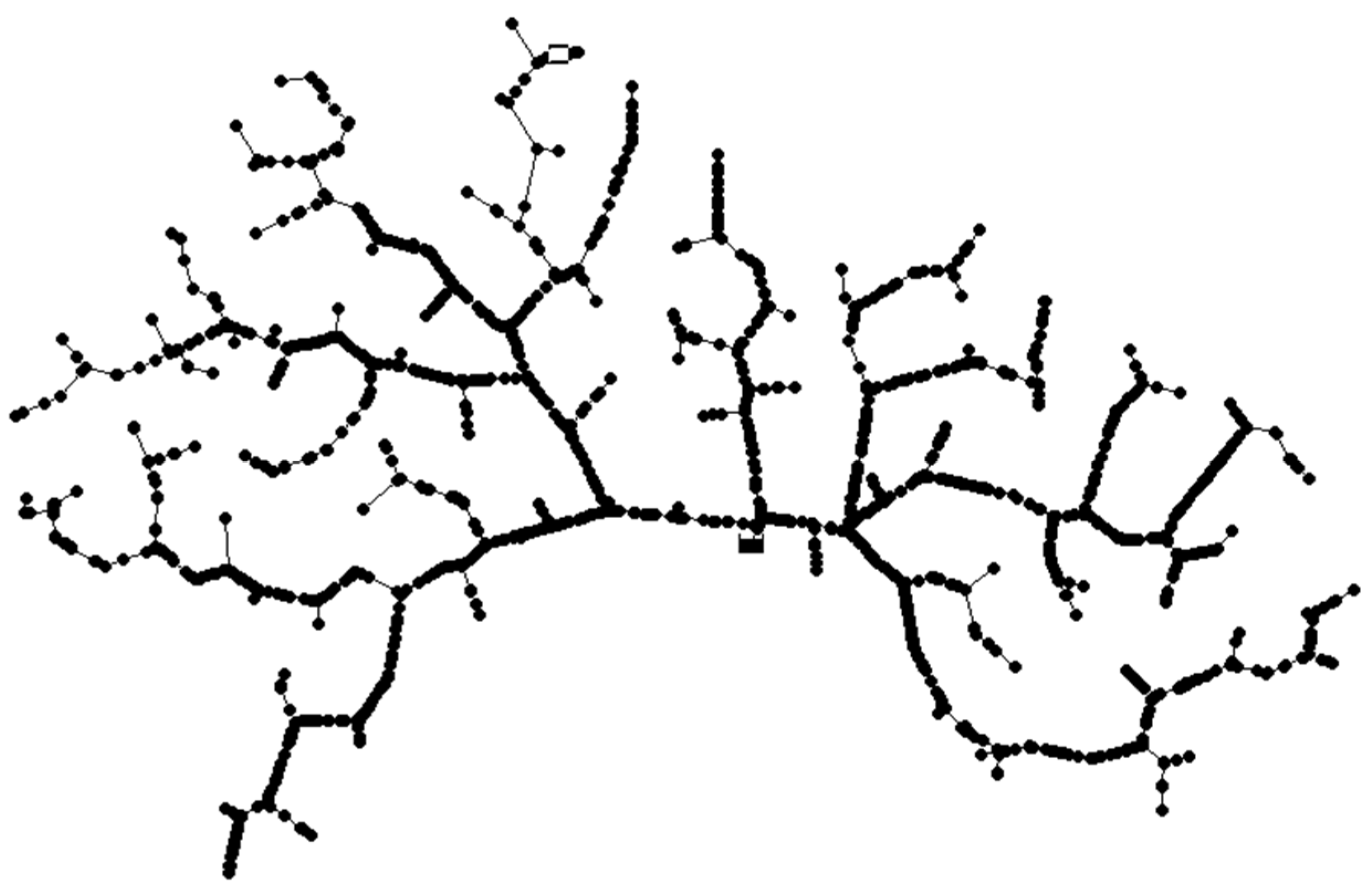
A case study network, the Zújar Canal irrigation district, was considered, which covers a surface of 20,870 ha divided into 10 pressurized irrigation sectors. In this study, irrigation sector II was investigated and the network layout is presented in Figure 1.

The network consists of 1790 pipes with diameters ranging between 80 and 1000 mm, suppling water to 196 hydrants, whose levels range between 250 m.a.s.l. and 285 m.a.s.l. The total number of nodes is 1791. The network was designed to supply 1.2 l/(s ha) on demand (i.e., 24 h per day), under the hypothesis of 100% of simultaneity (i.e., all hydrants simultaneously open). The service pressure required at the hydrant level is 35 m.

A telemetry system was installed within the irrigation district to record the hourly water demands through flow meters located at the 196 hydrants. In this study, the optimization procedure was implemented based on the daily average demand values at each hydrant for the whole 2020 irrigation season (i.e., from April 2020 to September 2020), which resulted in 168 average values. Hence, the optimization procedure was performed on 168 time intervals (${\mathrm{n}}_{\mathrm{d}}$), each one presenting a duration of 24 h.

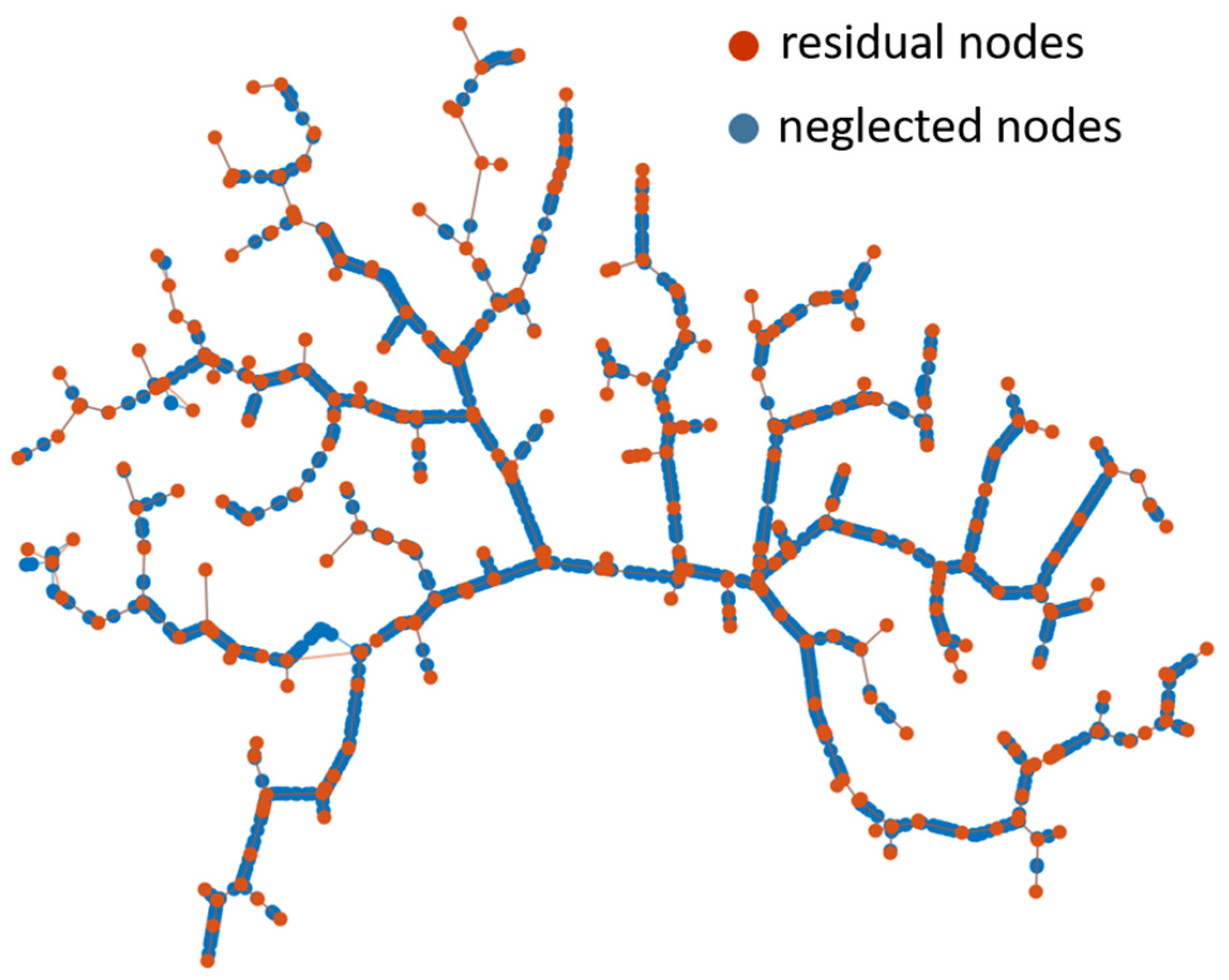
It is worth considering that the greater the number of time intervals and geometric elements (i.e., nodes and links), the more challenging the optimization. In order to deal with the large size of the network, skeletoning was performed. According to the implemented skeletoning procedure, a node $\mathrm{i}$ can be neglected if it demands a null flow, while the pipes approaching the $\mathrm{i}$-th node have same diameter and roughness. Figure 2 shows both the residual (orange dots) and neglected (blue dots) nodes within the network once the skeletoning is performed.

As shown in Figure 2, the network resulting from the skeletoning procedure is significantly simplified, with the number of nodes decreased from 1791 to 336.

3. The Optimization Procedure

3.1. Variables

The aim of the optimization procedure is to determine the best number and location of PATs within the network in order to maximize the energy production and minimize the investment cost. The presence of a turbine within a branch $\mathrm{k}$ of the network is modeled as a binary variable (${\mathrm{I}}_{\mathrm{k}}^{\mathrm{T}}$), which is equal to one if the device is installed and zero otherwise. The proposed optimization procedure does not interact with any external hydraulic solvers (e.g., EPANET); thus, the computation of flow through links (${\mathrm{Q}}_{\mathrm{k}}$) and the head nodes (${\mathrm{H}}_{\mathrm{i}}$) is carried out along with the optimization procedure by integrating the momentum balance and continuity equations within the optimization model as mathematical constraints. Moreover, with reference to the reservoir, its head is known and assumed to be constant during the whole simulation, whereas the unknown variable is the flowrate supplying the network (${\mathrm{q}}_{\mathrm{r}}$) at each time interval. The hydraulic resolution of the network, and in particular the need for modeling the flow direction within links, requires the use of non-differentiable functions (e.g., the absolute value, if function, etc.), which are not easily handled by global optimization solvers. To develop a mathematical model consisting of as many differentiable functions as possible, a further binary variable (${\mathsf{\zeta }}_{\mathrm{k}}$) is introduced, which splits the flow through links (${\mathrm{Q}}_{\mathrm{k}}$) into its positive and negative components (i.e., ${\mathrm{q}}_{\mathrm{k}}^{+}$ and ${\mathrm{q}}_{\mathrm{k}}^{-}$, respectively) [18], depending on the flow direction:

$$0\le {\mathrm{q}}_{\mathrm{k}}^{+}\le {\mathrm{Q}}_{\max }{\mathsf{\zeta }}_{\mathrm{k}}$$

(1)

$$0\le {\mathrm{q}}_{\mathrm{k}}^{-}\le {\mathrm{Q}}_{\max }\left(1-{\mathsf{\zeta }}_{\mathrm{k}}\right)$$

(2)

where ${\mathrm{Q}}_{\max }$ represents the bound of the variable.

As for the flow ${\mathrm{Q}}_{\mathrm{k}}$, the head drop within the PATs is also split by the use of the variable ${\mathsf{\zeta }}_{\mathrm{k}}$, resulting in (${\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}+}$, ${\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}-}$), bounded by the use of a maximum head loss, ${\mathrm{H}}_{{\mathrm{k}}_{\max }}$.

The independent variables can be accounted for as summarized in

Table 1. Summary of the binary (B) and continuous (C) independent variables of the proposed optimization problem.

Variable	${\mathrm{I}}_{\mathrm{k}}^{\mathrm{T}}$	${\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}+}\left(\mathsf{\theta }\right)$	${\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}-}\left(\mathsf{\theta }\right)$	${\mathsf{\zeta }}_{\mathrm{k}}\left(\mathsf{\theta }\right)$	${\mathrm{q}}_{\mathrm{k}}^{+}\left(\mathsf{\theta }\right)$	${\mathrm{q}}_{\mathrm{k}}^{-}\left(\mathsf{\theta }\right)$	${\mathrm{H}}_{\mathrm{i}}\left(\mathsf{\theta }\right)$	${\mathrm{q}}_{\mathrm{r}}\left(\mathsf{\theta }\right)$
Number	$\mathrm{l}$	$\mathrm{l}·{\mathrm{n}}_{\mathrm{d}}$	$\mathrm{l}·{\mathrm{n}}_{\mathrm{d}}$	$\mathrm{l}·{\mathrm{n}}_{\mathrm{d}}$	$\mathrm{l}·{\mathrm{n}}_{\mathrm{d}}$	$\mathrm{l}·{\mathrm{n}}_{\mathrm{d}}$	$\mathrm{n}·{\mathrm{n}}_{\mathrm{d}}$	$\mathsf{\varsigma }·{\mathrm{n}}_{\mathrm{d}}$
Type	B	C	C	B	C	C	C	C

, where $\mathsf{\theta }(\mathsf{\theta }=1\dots {\mathrm{n}}_{\mathrm{d}}$) represents the time interval. With reference to Table 1, the variables are classified as binary (B) or continuous (C).

3.2. Objective Function

As the objective function of the optimization procedure, the net present value (NPV) of the investment is assumed. Multi-objective functions would be not suitable for such a global optimization procedure. However, the maximization of the NPV maximizes the energy savings and minimizes the investment costs simultaneously.

$$\mathrm{NPV}={\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{l}}}\left(-{\mathrm{c}}_{\mathrm{k}}^{\mathrm{T}}{\mathrm{I}}_{\mathrm{k}}^{\mathrm{T}}\right)+{\displaystyle \sum _{\mathrm{y}=1}^{\mathrm{Y}}}\frac{{\mathrm{E}}_{\mathrm{y}}^{\mathrm{p}}}{{\left(1+\mathsf{\epsilon }\right)}^{\mathrm{y}}}$$

(3)

With reference to Equation (3), ${\mathrm{c}}_{\mathrm{k}}^{\mathrm{T}}{\mathrm{I}}_{\mathrm{k}}^{\mathrm{T}}$ represents the outflow cash due to the investment and is expressed as a negative quantity. Moreover, ${\mathrm{E}}_{\mathrm{y}}^{\mathrm{p}}$ is the energy revenue for the y-th irrigation season, $\mathsf{\epsilon }$ is the discount rate (fixed as 5%), and Y is the total number of irrigation seasons, set as 10. With regard to the investment cost, this is evaluated according to the cost model defined by Novara et al. [19]. With reference to the income resulting from the energy production, this is evaluated from the produced power (Equation (4)), assuming an energy unit selling price equal to 0.1 €/kWh.

$${\mathrm{P}}_{\mathrm{T}}=\mathsf{\gamma }\left({\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}+}+{\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}-}\right)\left({\mathrm{q}}_{\mathrm{k}}^{+}+{\mathrm{q}}_{\mathrm{k}}^{-}\right){\mathsf{\eta }}^{\mathrm{T}}$$

(4)

In Equation (4), $\mathsf{\gamma }$ is the specific weight of water and ${\mathsf{\eta }}^{\mathrm{T}}$ is the PAT efficiency, which is set as 0.65. It is worth underlining that in this study the devices are modeled as head losses within pipes, since the aim of this work is to search for the optimal location for the devices, as well as to evaluate the energy potential of the case study network. However, the design could be carried out in a second phase, once the optimal location is found.

Finally, to reduce the research space and push the solver to find a good quality solution, a minimum value of the maximum producible power (${\mathrm{P}}_{\mathrm{k},\max }$) during the irrigation season is introduced:

$${\mathrm{P}}_{\mathrm{k},\max }>={\mathrm{P}}_{\min }{\mathrm{I}}_{\mathrm{k}}^{\mathrm{T}}$$

(5)

where ${\mathrm{P}}_{\min }$ is set as equal to 1 kW.

3.3. Global Optimization Solver

In the analyzed problem, since the variables are both integers and continuous, and the constraints are both linear and non-linear and the resulting model involves mixed-integer non-linear programming (MINLP) [20].

MINLP problems are the most challenging optimization problems in the field of operational research. Many deterministic solvers for MINLPs exist, but most of these achieve the global optimum only in convex problems, otherwise they retrieve heuristic solutions. Since the study of problem convexity is not straightforward, in this study an SCIP (solving constraint integer program) solver [21] is selected, being a global optimal solver suitable for both convex ad non-convex MINLP problems. Implementing a spatial branch and bound, the SCIP potentially finds the global optima. Despite this, the time required by the solver to reach convergence may even be infinite. For this reason, SCIP solvers are frequently used to also find the local optima. The power of using a global optimization solver to find the local optima lies in the possibility for the user to evaluate the effectiveness of the found solution as compared to heuristic methods, which do not even give a general idea about the quality of the found solutions. In particular, SCIP provides the user with the relative gap between the found solution and the upper bound (or lower bound if minimizing) of the problem, obtained by means of a relaxation of the problem. During the computation, the solver reduces the upper bound (or increases the lower bound if minimizing) and improves the solution; thus, the relative gap is progressively reduced. When a global optimum is found, the upper bound and the solution value are the same; that is, the relative gap is zero. Despite the enormous power, the drawback of using such a global optimization solver lies in the mathematical requirements (i.e., a mathematical model mainly consisting of differentiable functions), as well as in the strong computational effort.

3.4. The Mathematical Model

The optimization procedure, along with the hydraulic resolution of the network, is integrated in one single mathematical model, as presented in Equation (5). It is worth clarifying that for the sake of brevity in the notation, in this model the dependence on the time interval is omitted.

The total number of variables amounts to 313,077 (i.e., 670 binary and 312,407 continuous variables), whereas the total number of mathematical constraints is equal to 749,099.

With reference to the momentum balance equation (see model in Equation (6)), the resistance term (${\mathrm{r}}_{\mathrm{k}}$) within each pipe k is evaluated using the Darcy–Weisbach formula, where the friction factor is computed according to Swamee–Jain correlation [22]. This correlation approximates the implicit Colebrook–White equation and is one of the main expressions used to directly solve the Darcy–Weisbach friction factor for a full-flowing circular pipe [23].

Finally, as shown in Equation (6), once the node elevation (${\mathrm{z}}_{\mathrm{i}}$) is known, the pressure at the nodes (i.e., ${\mathrm{H}}_{\mathrm{i}}-{\mathrm{z}}_{\mathrm{i}}$) is bounded between two fixed minimum and maximum values, set at 35 m and 100 m, respectively.

$$\{\begin{array}{c}\begin{array}{cc}\begin{array}{c}\mathrm{maximize}\\ {\mathrm{I}}_{\mathrm{k}}^{\mathrm{T}},{\mathsf{\zeta }}_{\mathrm{k}}\\ {\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}+},{\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}-}\\ {\mathrm{q}}_{\mathrm{k}}^{+},{\mathrm{q}}_{\mathrm{k}}^{-},{\mathrm{H}}_{\mathrm{i}},{\mathrm{q}}_{\mathrm{i}}^{\mathrm{d}}\end{array}& \mathrm{NPV}={\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{l}}}\left(-{\mathrm{c}}_{\mathrm{k}}^{\mathrm{T}}{\mathrm{I}}_{\mathrm{k}}^{\mathrm{T}}\right)+{\displaystyle \sum _{\mathrm{y}=1}^{\mathrm{Y}}}\frac{{\mathrm{E}}_{\mathrm{y}}^{\mathrm{p}}}{{\left(1+\mathsf{\epsilon }\right)}^{\mathrm{y}}}\\ \mathrm{subject}\mathrm{to}& \begin{array}{c}0\le {\mathrm{q}}_{\mathrm{k}}^{+}\le {\mathrm{Q}}_{\max }{\mathsf{\zeta }}_{\mathrm{k}}\\ 0\le {\mathrm{q}}_{\mathrm{k}}^{-}\le {\mathrm{Q}}_{\max }\left(1-{\mathsf{\zeta }}_{\mathrm{k}}\right)\\ 0\le {\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}+}\le {\mathrm{H}}_{{\mathrm{k}}_{\max }}{\mathsf{\zeta }}_{\mathrm{k}}\\ 0\le {\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}-}\le {\mathrm{H}}_{{\mathrm{k}}_{\max }}\left(1-{\mathsf{\zeta }}_{\mathrm{k}}\right)\\ {\displaystyle \sum _{\mathrm{k}\in {\mathrm{K}}_{\mathrm{i}}}}{\left({\mathrm{q}}_{\mathrm{k}}^{+}+{\mathrm{q}}_{\mathrm{k}}^{-}\right)}^{\mathrm{in}}-{\displaystyle \sum _{\mathrm{k}\in {\mathrm{K}}_{\mathrm{i}}}}{\left({\mathrm{q}}_{\mathrm{k}}^{+}+{\mathrm{q}}_{\mathrm{k}}^{-}\right)}^{\mathrm{out}}-{\mathrm{q}}_{\mathrm{i}}^{\mathrm{d}}=0\\ {\mathrm{H}}_{\mathrm{i}}-{\mathrm{H}}_{\mathrm{j}}-{\mathrm{r}}_{\mathrm{k}}{\mathrm{L}}_{\mathrm{k}}-({\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}+}-{\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}-})=0\\ {\mathrm{P}}_{\mathrm{k}}=\mathsf{\gamma }\left({\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}+}+{\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}-}\right)\left({\mathrm{q}}_{\mathrm{k}}^{+}+{\mathrm{q}}_{\mathrm{k}}^{-}\right){\mathsf{\eta }}^{\mathrm{T}}\\ {\mathrm{P}}_{\mathrm{k},\max }>={\mathrm{P}}_{\min }{\mathrm{I}}_{\mathrm{k}}^{\mathrm{T}}\\ \frac{{\mathrm{p}}_{\min }}{\mathsf{\gamma }}\le \left({\mathrm{H}}_{\mathrm{i}}-{\mathrm{z}}_{\mathrm{i}}\right)\le \frac{{\mathrm{p}}_{\max }}{\mathsf{\gamma }}\\ {\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}}\le {\mathrm{H}}_{{\mathrm{k}}_{\max }}{\mathrm{I}}_{\mathrm{k}}^{\mathrm{T}}\\ 0\le {\mathrm{I}}_{\mathrm{k}}^{\mathrm{T}}\le 1\\ 0\le {\mathsf{\zeta }}_{\mathrm{k}}\le 1\\ ({\mathrm{I}}_{\mathrm{k}}^{\mathrm{T}})\in \mathbb{Z},\hspace{1em}\hspace{1em}\left({\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}+},{\mathrm{H}}_{\mathrm{k}}^{\mathrm{T}-},{\mathrm{H}}_{\mathrm{i}},{\mathrm{P}}_{\mathrm{k}}\right)\in ℝ,\\ \left({\mathrm{q}}_{\mathrm{k}}^{+},{\mathrm{q}}_{\mathrm{k}}^{-}\right)\in ℝ,\hspace{1em}\hspace{1em}⩝\mathrm{i},\mathrm{j}=1\dots \mathrm{n},\hspace{1em}\hspace{1em}⩝\mathrm{k}=1\dots {\mathrm{n}}_{\mathrm{l}}\end{array}\end{array}\end{array}$$

(6)

The code was developed using A Mathematical Programming Language (AMPL) [24], which is an algebraic modeling language supporting many optimization solvers. Finally, the optimization was performed on an Intel @ Xeon(R) CPU E5-2620 v4 @ 2.10 GHz x 16 with 64 GB RAM.

4. Results

The results of the optimization procedure are shown in

Table 2. Solution of the optimization procedure—the global optimum.

	NPV (€)	No of PATs (-)	Energy Production (kWh/Season)	Investment Cost (€)
Global optimization	304,661	7	462,447	52,430

. The time required by the solver to achieve the solution was 1000 s. Nevertheless, it is worth underlining that the computation was protracted by up to 900 min in order to let the solver properly reduce the bound of the problem and provide reasonable information about the solution quality. At the end of the optimization, the solver provided a gap value equal to 0%; thus, the solution was definitely a global optimum.

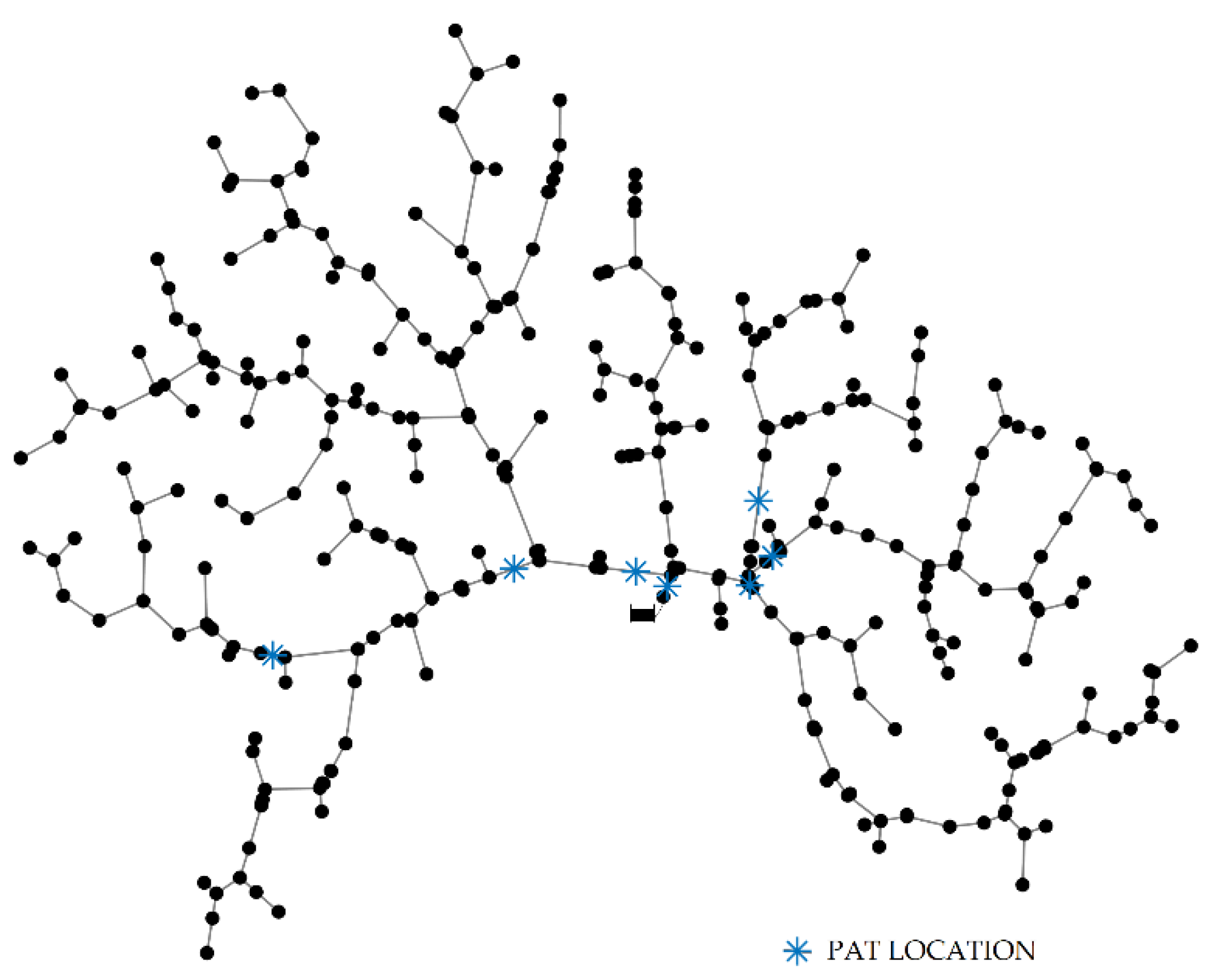
With reference to Table 1, the optimal solution consists of an NPV value equal to 304,661 €. The total number of installed devices is equal to 7, whose location is presented in Figure 3, and the corresponding investment cost amounts to 52,430 €.

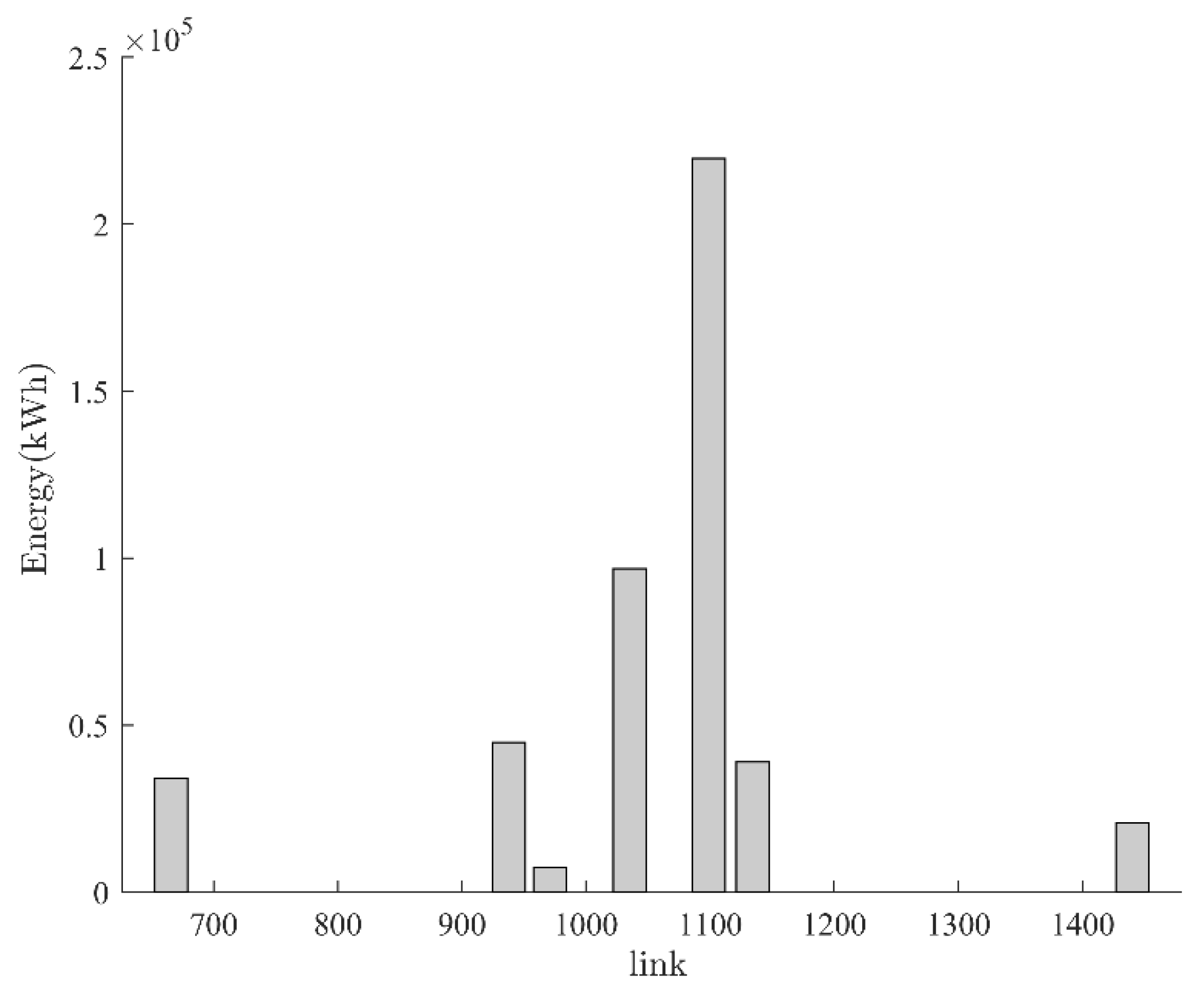
With regard to the inflow cash, this was accounted for as 46,245 € per year, with energy production equal to 462,447 kWh for the whole irrigation season. The total energy production within the links selected for PAT installation is presented in Figure 4.

5. Conclusions

In this study, the optimal location of PATs within an irrigation network has been investigated with the aim of maximizing the energy recovery and minimizing the investment costs. A case study, the Zújar Canal irrigation district, was considered, where accurate records of hourly water demands were available for the whole 2020 irrigation season. The hydraulic resolution of the network along with the optimization procedure were integrated in one single mathematical model, which was then solved using a global optimization solver. Despite the size of the optimization problem, consisting of 313,077 variables (both binary and continuous) and 749,099 constraints, the solution was achieved in a very reasonable time (i.e., 1000 s). Since the gap value provided by the solver is equal to zero, the found solution is the global optimum of the problem. According to the found solution, considering a useful life of 10 years and a discount rate equal to 5%, the NPV is 304,661 €, of which the investment cost for the installation of the 7 selected PATs is equal to 52,430 €. The resulting amount of produced energy was evaluated as 462,447 kWh for the whole six-month irrigation season.

Future studies will be focused on the design of the selected PATs in order to develop a more comprehensive and realistic optimization procedure. This could be achieved by either implementing a two-step procedure (i.e., in the first step searching for the optimal location and in the second step dealing with the optimal design) or by attempting to develop a one-step procedure to seek out the optimal location and design simultaneously. Despite being more reliable, the one-step procedure would result in strong computational complexities, which could be tackled via the use of new relaxation and decomposition techniques.