Abstract
In this work, we present the application of an alternative numerical model for fluid dynamic analyses of structural systems within the Smoothed Particle Hydrodynamics (SPH) framework of DualSPHysics coupled to the Project Chrono library. The Discrete Elements Method-based (DEM) structure model relies on the Euler–Bernoulli theory and utilizes lumped elasticity and rigid body dynamics to reproduce the flexural behavior of two-dimensional beams. The structure and fluid domain are both discretized with SPH particles: the fluid dynamics obey a Weakly Compressible SPH (WCSPH) formulation, whereas the structure particles are assembled into DEM rigid elements, moving according to physically-based, properly developed rotational dynamics. The presented model is of interest for studying complex soil–, solid–, fluid–structure interactions, involving a system that includes all the aforementioned phases in a unitary context—very useful for studying engineered structures under the threat of hazardous natural events. Test cases are presented to validate the SPH-DEM coupled model in both accuracy and stability, starting from an equilibrium test, to the dynamic response, and ending with fluid–structure interaction simulations. This work proves that the developed theory can be used within a Lagrangian framework, using the features provided by a DEM solver, overtaking the intrinsic limitations, and hence applying the results of static theory to complex dynamic problems.
1. Introduction
With the development of powerful computational tools, fluid–structure interaction (FSI) simulations are becoming standard in many application fields [1], as the reliability and flexibility of numerical models give the opportunity to enhance several engineering endeavors where the coupled effects are non-negligible.
The traditional approach to FSI considered mesh-based methods with a partitioned approach, where the Finite Element Method (FEM) treated the structure separately. However, computational costs due to re-meshing processes and convergence issues, led to alternative meshless approaches being considered. The Lagrangian methods are naturally structured to avoid the common drawbacks of grid-based methods, providing a robust computational tool to enhance the fluid phase simulation in FSI problems. Among this methods, the Meshfree Particle Methods (MPMs) gained much interest in many research fields and engineering applications. The MPMs employ a set of a finite number of discrete particles to represent the state of a system and to record its movement: each particle can either be directly associated with one discrete physical object, or be generated to represent a part of the continuum problem domain [2]. These methods provide a robust computational tool to handle fluid phases characterized by relevant deformations, as moving boundaries and complex interfaces are easily tracked by assigning particular physical quantities to each computational point (particle). One of the most used Lagrangian approaches in recent years has been the Smoothed Particle Hydrodynamics (SPH) method [3], especially regarding coastal engineering applications, but, in general, in all water-related fields [4,5].
Fully Lagrangian approaches have been used for the FSI application, where both fluids and solids are modeled within the same SPH framework: for example, the ISPH-SPH framework by Khayyer et al. (2022) [6] or the SPH-total Lagrangian SPH solver by Sun et al. (2019) [7]. Other coupled solutions pair an SPH fluid phase with a structural solver [8] to exploit the strengths of both numerical schemes. Along this path, the proposed work showcases the reliability of an alternative coupled framework, developed in Capasso et al. (2022) [9], composed of a Discrete Elements Method (DEM) structure solver within a homogeneous SPH environment. The DEM model, suitable for breakage, rupture and large deformations phenomena [10], is developed starting from the Euler–Bernoulli beam theory [11] by a lumped elasticity approach. It follows a set of rigid elements connected by relative constraints implemented in the DualSPHysics framework that allows the simulation of a wide range of flexible elements.
DualSPHysics is an open-source software based on the SPH method [12]. Its highly parallelized structure harnesses the computing power of graphics processing unit (GPU) cards [13]. The capability of DualSPHysics to address complex multiphysics applications has been enhanced by its coupling with other numerical models [13,14,15]. In particular, thanks to the coupling to the Project Chrono multiphysics library [16], it can simulate complex mechanical systems and multibody problems. The effectiveness of the DualSPHysics-Chrono framework, including multibody dynamics simulations and mechanical constraints, has been extensively proved [14,15,17,18]. Within the field of renewable energy, many successful applications have been presented over the last years [19,20,21,22].
Two FSI test cases for the SPH-DEM model are presented here to showcase the applicability of the proposed scheme. The theoretical fundamentals of the SPH-DEM scheme are briefly introduced in Section 2, while the benchmark tests are shown in Section 3. Final considerations and further possible developments can be found in Section 4.
2. SPH-DEM Fundamentals
2.1. Fluid Phase
The strategy in SPH is to discretize the physical domain (fluid and/or solid objects) into a set of particles, where the physical quantities are obtained as an interpolation of the corresponding quantities of the surrounding particles. The contribution of those particles is weighted using a kernel function, with an area of influence that is defined using a characteristic smoothing length [2].
The integral representation of a generic spatial function within an integral volume Ω, is given by
where is the smoothing kernel function or kernel, whereas is the position vector. In the smoothing function, is the smoothing length defining the influence area of .
Within a discrete space, the function is approximated by summing up the values of the nearest neighbor particles that possess fixed mass and finite volume . The discrete form of Equation (1) for a particle , being part of its support domain
The kernel function, hence, plays a fundamental role in the SPH method. In DualSPHysics the Wendland quintic kernel function [23] has been utilized.
2.1.1. Governing Equations
The fluid domain behaves according to the Navier–Stokes (NS) equations
where is the density, is the velocity vector, the gravitational acceleration vector, is the pressure and is the deviatoric stress tensor. An extensive treatise of the Weakly Compressible SPH (WCSPH) discretization of the NS equations can be found in [9].
2.1.2. Boundary Treatment
Dynamic Boundary Conditions (DBC) [24] for solid surfaces are standard in DualSPHysics [25]. Solids are represented by fixed particles whose pressure is dependent on the same state equation as the fluid particles.
To enhance the DBC formulation, the modified Dynamic Boundary Conditions (mDBC) [26] has been developed and validated [27,28]. The particle arrangement remains the same as in the DBC, while a mirroring technique [29] helps compute smoother pressure fields by using ghost nodes located in the fluid domain, where the properties are found through a first-order consistent SPH spatial interpolation [30] over the surrounding fluid particles only. In this way the fixed boundaries are presented as a part of a fluid mass, avoiding any non-physical separation between particles.
2.1.3. Rigid Body Dynamics and Coupling Strategy
The rigid bodies in the DualSPHysics environment are discretized with a different set of particles, which obey Newton’s law for the rigid body dynamics [14,31]. The force per unit of mass experienced by a boundary particle is
where is the unitary force exerted by the fluid particle on the boundary particle .
The interaction between bodies is handled by the Project Chrono module embedded in the original framework of DualSPHysics: arbitrarily defined structures with dynamic- and kinematic-type restrictions can be simulated by the Chrono library integrating active and reactive forces. DualSPHysics calculates the forces exerted on the bodies by the fluid particles, while Project Chrono updates their position , angular and linear velocities [9].
2.2. Structure Model
The DEM model formulation presented in Capasso et al. (2022) [9,32] relies on the assumptions of the Euler–Bernoulli (EB) beam theory, which lead to ordinary differential equations able to describe the static beam deformation through linear elasticity relations called constitutive bonds. If the flexural behavior is considered, as a matter of course in many engineering applications, the bending moment, , governs the deflection of the beam with a rotation rate per cross-section defined by
with being the Young’s modulus, and the second moment of inertia of the cross-section.
Considering the rotation finite () costs an error proportional to the dimension of the interval (). The rotational stiffness of the whole trunk, hence, is lumped in a single point, namely the rotational hinge: in this way, the deformation function is represented by a physical set of linear interpolating polynomials (trunks) that rotate according to the geometrical and mechanic characteristics of the beam. If the beam is divided in trunks of dimension , then the element rotation with respect to the hinge is given by
where is the local rotation, and is the total reactive moment. The constant quantities in Equation (7) are referred to as rotational stiffness
As a matter of fact, this numerical solution allows a straightforward implementation within the DualSPHysics + Chrono framework: each trunk is modeled as a rigid floating object, while the rotational constraint reactions that reproduce the elasticity of the beam are computed by the Chrono library. Being governed by the rigid body dynamics, the co-rotating elements, modeled upon static hypotheses, can reproduce the flexural behavior of thin beams in complex dynamics and multiphysics phenomena.
3. Applications
3.1. A Breaking Water-Column with an Elastic Gate
This FSI benchmark was first presented in Antoci et al. (2007) [33], in which the experimental setup and results in a two-dimensional fashion are provided; a schematic of the setup is given in Figure 1. The water-column, kg/m3, is confined between two rigid walls, one of these with an elastic gate at its end. The latter is modeled with the proposed SPH-DEM scheme to reproduce the elastic deformation induced by the fluid pressure. The experimental reference given in [33] is compared to the displacement of the free-end of the gate in the first instants of the simulation.
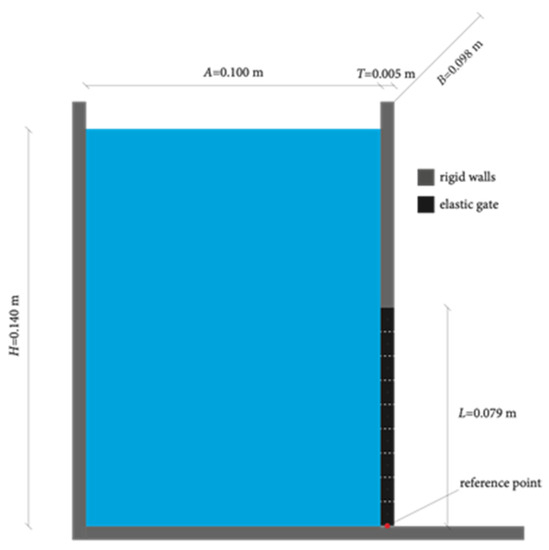
Figure 1.
Setup of the benchmark after Antoci et al. (2007) [33] in DualSPHysics.
The results displayed in Figure 2, together with the snapshot comparison in Figure 3, describe an overall acceptable agreement, especially between the presented model and the iSPH-SPH model proposed by Khayyer et al. (2018) [6]. The latter solver is based on a coupled model in which the fluid is treated as incompressible, thus ensuring great stability by the way of a semi-implicit projection-based particle method (iSPH), and an SPH-based structure model. Differently from the explicit WCSPH implementation available in DualSPHysics, the iSPH solver admits larger time-steps and globally solves the fluid–structure interaction, as the computation of pressure follows from the Poisson’s equation instead of the very stiff Tate’s equation [9].
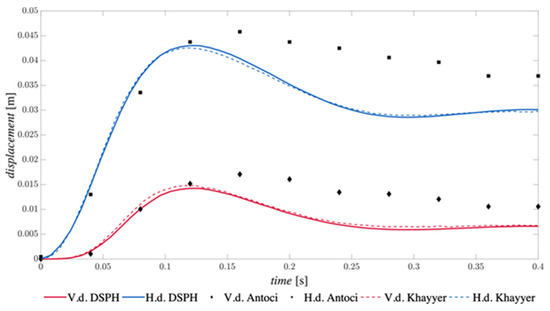
Figure 2.
Horizontal and vertical free-end displacements time history with , paired with experimental results from [33] and iSPH simulations from [6].
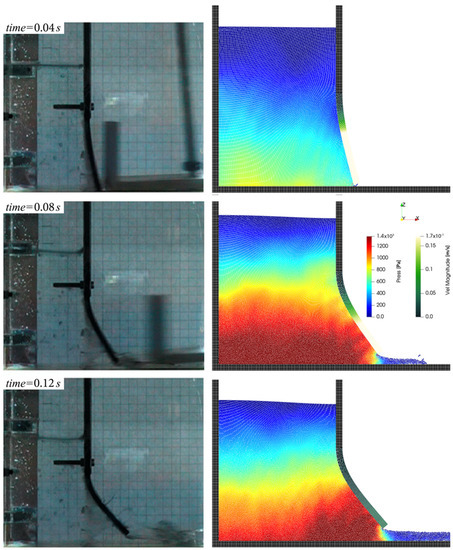
Figure 3.
Breaking water-column numerical test: comparison between photos from experiment [33] (left) and SPH-DEM results (right) at different time instants.
In the first instance of the simulation, the SPH-DEM scheme properly follows the experimental data, while, after the peak of deformation, it appears to be excessively rigid. This behavior is probably due to the absence of damping in the beam, which will require further investigation. The visual comparison (Figure 3) highlights a smooth pressure field, and confirms the good reproduction of the first instance of the simulation. At time s, the velocity magnitude of the elastic gate is approximately null, in correspondence with the peak of deformation, when the resistance of the structure equalizes the dynamic fluid load.
3.2. Hydroelastic Slamming of an Aluminium Wedge
The following benchmark consists of a high-speed impact of a deformable aluminum beam with the undisturbed water surface. A semi-analytic solution was made available by [34], while numerical simulations are performed in [6]; both of the references were obtained under incompressible fluid hypothesis. The wedge is composed of two symmetrical wings of length m and thickness m, tilted at an angle of with respect to the water surface. The Young’s modulus of the beam is GPa, while the Poisson’s coefficient is . The elastic structure impacts the water at a fixed velocity m/s, with the central section, as well as the extremities, restrained to a vertical motion without any other degree of freedom. Consistently with this hypothesis formulated by [34], the DualSPHysics setup is built according to Figure 4, with the rigid trunks disposed perpendicularly to the slope and fitted at the far ends.
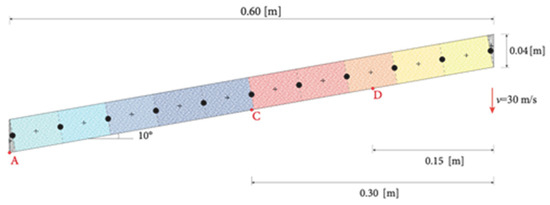
Figure 4.
Wedge wing Chrono scheme, with the trunks’ (in different colors) and hinges’ disposition visible; in red the reference points for pressure and displacement computation.
In the following chart an SPH resolution of , with being the initial interparticle distance, is used.
The numerical speed of sound for the fluid phase is set at m/s to properly simulate the highly dynamics phenomenon, and therefore very small time-steps are required.
In Figure 5 the displacement of the point C is presented: results with two different DEM resolutions, depending on the parameter , are paired with the semi-analytical and numerical references, showing good agreement. As the number of trunks increases, the behavior of the SPH-DEM model tends to resemble the semi-analytical one: the inflection point, around s, when the elastic response of the structure begins to counter the fluid action, is better reproduced as expected.
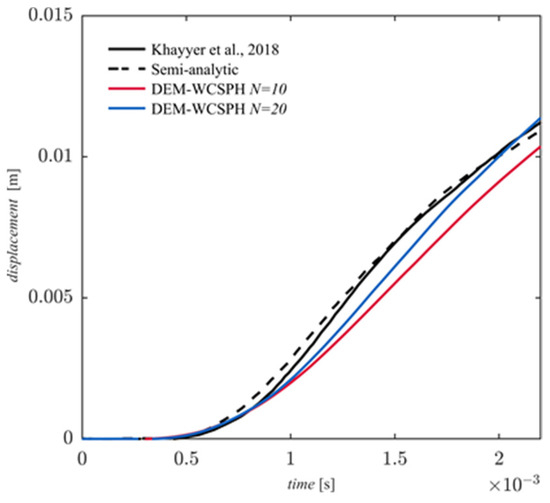
Figure 5.
Time history of the deflection at point C, with two different DEM resolutions .
4. Outlook
The proposed approach makes the most out of the fluid–solid interaction computation capability of the DualSPHysics solver, exploiting the potentiality of the solid body motion solver of the embedded Chrono module to handle complex hydroelastic phenomena, in which the mutual exchange of forces, pressure and viscous stress between the fluid and structure plays a fundamental role.
The presented model relies on the EB hypotheses, but has a broader application field: the validations proposed account for deformations clearly out of the limits imposed by the beam theory but are, anyway, properly reproduced. Furthermore, the inherent nature of the SPH environment where the model is developed allows the direct tracking of interfaces, efficient body force computation and extreme displacements reproduction.
The straightforward implementation procedure of the SPH-DEM model provides a reliable tool, which relies on the well-known capabilities of Smoothed Particle Hydrodynamics, to approach the study of the elastic response of structures through a Discrete Element model. The presented model, hence, can be applied to several real-world engineering problems, for example:
- flow–structure interactions involving coastal vegetation, i.e., bioshields;
- swinging of wind turbine columns subject to waves or seismic action;
- modeling of vibrations of one-dimensional structures interacting with Newtonian or non-Newtonian fluids.
All these fields involve non-negligible coupled effects that need similar numerical frameworks to be correctly assessed, as the optimization of the resources, especially among the emerging renewable technologies, is probably the cornerstone to fully exploit the energy potential stored in our environment. Advanced numerical models, such as the one proposed, indeed, are developed to further enhance the design of systems that require an in-depth analysis of wave– and, in general, fluid–structure interaction.
Further improvements could enhance the performances and widen the application possibilities: including the deformation effects due to the shear and normal stress, or even model elasto-plastic behavior.
Author Contributions
Conceptualization, S.C., B.T. and G.V.; methodology, S.C., B.T., G.V.; software, S.C. and B.T.; validation, S.C. and B.T.; formal analysis, S.C.; investigation, S.C. and B.T.; resources, G.V.; writing—original draft preparation, S.C.; writing—review and editing, B.T., S.C. and G.V.; visualization, S.C.; supervision, G.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shadloo, M.; Oger, G.; Le Touzé, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Liu, G.; Liu, M. Smoothed Particle Hydrodynamics; World Scientific: Singapore, 2003. [Google Scholar] [CrossRef]
- Violeau, D.; Rogers, B. Smoothed particle hydrodynamics (SPH) for free-surface flows: Past, present and future. J. Hydraul. Res. 2016, 54, 1–26. [Google Scholar] [CrossRef]
- Gotoh, H.; Khayyer, A. On the state-of-the-art of particle methods for coastal and ocean engineering. Coast. Eng. J. 2018, 60, 79–103. [Google Scholar] [CrossRef]
- Manenti, S.; Wang, D.; Domínguez, J.; Li, S.; Amicarelli, A.; Albano, R. SPH Modeling of Water-Related Natural Hazards. Water 2019, 11, 1875. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Falahaty, H.; Shimizu, Y. An enhanced ISPH-SPH coupled method for simulation of incompressible fluid-elastic structure interactions. Comput. Phys. Commun. 2018, 232, 139–164. [Google Scholar] [CrossRef]
- Sun, P.; Le Touzé, D.; Zhang, A.M. Study of a complex fluid-structure dam-breaking benchmark problem using a multi-phase SPH method with APR. Eng. Anal. Bound. Elem. 2019, 104, 240–258. [Google Scholar] [CrossRef]
- Fourey, G.; Hermange, C.; Le Touzé, D.; Oger, G. An efficient FSI coupling strategy between Smoothed Particle Hydrodynamics and Finite Element methods. Comput. Phys. Commun. 2017, 217, 66–81. [Google Scholar] [CrossRef]
- Capasso, S.; Tagliafierro, B.; Martínez-Estévez, I.; Domínguez, J.M.; Crespo, A.J.C.; Viccione, G. A DEM approach for simulating flexible beam elements with the Project Chrono core module in DualSPHysics. Comput. Part. Mech. 2022, 9, 969–985. [Google Scholar] [CrossRef]
- Fleissner, F.; Gaugele, T.; Eberhard, P. Applications of the discrete element method in mechanical engineering. Multibody Syst. Dyn. 2007, 18, 81–94. [Google Scholar] [CrossRef]
- Bauchau, O.A.; Craig, J.I. Euler-Bernoulli Beam Theory. In Structural Analysis; Bauchau, O.A., Craig, J.I., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 173–221. [Google Scholar] [CrossRef]
- Domínguez, J.; Fourtakas, G.; Altomare, C.; Canelas, R.; Tafuni, A.; García Feal, O.; Martínez-Estévez, I.; Mokos, A.; Vacondio, R.; Crespo, A.; et al. DualSPHysics: From fluid dynamics to multiphysics problems. Comput. Part. Mech. 2021, 9, 867–895. [Google Scholar] [CrossRef]
- Altomare, C.; Viccione, G.; Tagliafierro, B.; Bovolin, V.; Domínguez, J.; Crespo, A. Free-Surface Flow Simulation with Smoothed Particle Hydrodynamics Method using High-Performance Computing. In Computational Fluid Dynamics: Basic Instruments and Applications in Science; IntechOpen: London, UK, 2018; pp. 73–100. [Google Scholar] [CrossRef][Green Version]
- Domínguez, J.; Crespo, A.; Hall, M.; Altomare, C.; Wu, M.; Stratigaki, V.; Troch, P.; Cappietti, L.; Gómez-Gesteira, M. SPH simulation of floating structures with moorings. Coast. Eng. 2019, 153, 103560. [Google Scholar] [CrossRef]
- Canelas, R.; Brito, M.; Feal, O.; Domínguez, J.; Crespo, A. Extending DualSPHysics with a Differential Variational Inequality: Modeling fluid-mechanism interaction. Appl. Ocean Res. 2018, 76, 88–97. [Google Scholar] [CrossRef]
- Tasora, A.; Serban, R.; Mazhar, H.; Pazouki, A.; Melanz, D.; Fleischmann, J.; Taylor, M.; Sugiyama, H.; Negrut, D. Chrono: An Open Source Multi-physics Dynamics Engine. In High Performance Computing in Science and Engineering; Kozubek, T., Blaheta, R., Šístek, J., Rozložník, M., Čermák, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 19–49. [Google Scholar] [CrossRef]
- Ruffini, G.; Briganti, R.; De Girolamo, P.; Stolle, J.; Ghiassi, B.; Castellino, M. Numerical Modelling of Flow-Debris Interaction during Extreme Hydrodynamic Events with DualSPHysics-CHRONO. Appl. Sci. 2021, 11, 3618. [Google Scholar] [CrossRef]
- Brito, M.; Canelas, R.; García-Feal, O.; Domínguez, J.; Crespo, A.; Ferreira, R.; Neves, M.; Teixeira, L. A numerical tool for modelling oscillating wave surge converter with nonlinear mechanical constraints. Renew. Energy 2020, 146, 2024–2043. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.; Tagliafierro, B.; Altomare, C.; Domínguez, J.; Gómez-Gesteira, M.; Viccione, G. Efficiency and survivability analysis of a point-absorber wave energy converter using DualSPHysics. Renew. Energy 2020, 162, 1763–1776. [Google Scholar] [CrossRef]
- Tagliafierro, B.; Montuori, R.; Vayas, I.; Ropero-Giralda, P.; Crespo, A.; Domìnguez, J.; Altomare, C.; Viccione, G.; Gòmez-Gesteira, M. A new open-source solver for modelling fluid-structure interaction: Case study of a point-absorber wave energy converter with a power take-off unit. In Proceedings of the 11th International Conference on Structural Dynamics, Athens, Greece, 23–26 November 2020. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.; Coe, R.; Tagliafierro, B.; Domínguez, J.; Bacelli, G.; Gómez-Gesteira, M. Modelling a Heaving Point-Absorber with a Closed-Loop Control System Using the DualSPHysics Code. Energies 2021, 14, 760. [Google Scholar] [CrossRef]
- Tagliafierro, B.; Martínez-Estévez, I.; Domínguez, J.M.; Crespo, A.J.; Göteman, M.; Engström, J.; Gómez-Gesteira, M. A numerical study of a taut-moored point-absorber wave energy converter with a linear power take-off system under extreme wave conditions. Appl. Energy 2022, 311, 118629. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial basis functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Knio, O. SPH Modelling of Water Waves. In Proceedings of the Fourth Conference on Coastal Dynamics, Lund, Sweden, 11–15 June 2001; pp. 779–787. [Google Scholar] [CrossRef]
- Crespo, A.J.; Gómez-Gesteira, M.; Dalrymple, R.A. Boundary Conditions Generated by Dynamic Particles in SPH Methods. Comput. Mater. Contin. 2007, 5, 173–184. [Google Scholar] [CrossRef]
- English, A.; Domínguez, J.; Vacondio, R.; Crespo, A.; Stansby, P.; Lind, S.; Chiapponi, L.; Gómez-Gesteira, M. Modified dynamic boundary conditions (mDBC) for general purpose smoothed particle hydrodynamics (SPH): Application to tank sloshing, dam break and fish pass problems. Comput. Part. Mech. 2021, 9, 1–15. [Google Scholar] [CrossRef]
- Capasso, S.; Tagliafierro, B.; Güzel, H.; Yilmaz, A.; Dal, K.; Kocaman, S.; Viccione, G.; Evangelista, S. A Numerical Validation of 3D Experimental Dam-Break Wave Interaction with a Sharp Obstacle Using DualSPHysics. Water 2021, 13, 2133. [Google Scholar] [CrossRef]
- González-Cao, J.; Domínguez, J.; Crespo, A.; Gesteira, M.; Wang, S.; Islam, H.; Guedes-Soares, C. FSI problems with DualSPHysics: Analysis of the Modified Dynamic Boundary Conditions. In Proceedings of the 5th DualSPHysics Users Workshop, online, 5–17 March 2021. [Google Scholar]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touzé, D.; Graziani, G. δ-SPH model for simulating violent impact flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Liu, M.; Liu, G. Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 2006, 56, 19–36. [Google Scholar] [CrossRef]
- Monaghan, J.; Kos, A.; Issa, N. Fluid Motion Generated by Impact. J. Waterw. Port Coast. Ocean. Eng. 2003, 129, 250–259. [Google Scholar] [CrossRef]
- Capasso, S.; Tagliafierro, B.; Martínez-Estévez, I.; Domínguez, J.M.; Rahi, J.E.; Stratigaki, V.; Crespo, A.J.C.; Montuori, R.; Troch, P.; Gómez-Gesteira, M.; et al. On the development of a novel approach for simulating elastic beams in dualsphysics with the use of the project Chrono library. In Proceedings of the 8th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2021), Athens, Greece, 28–30 June 2021; pp. 4385–4399. [Google Scholar] [CrossRef]
- Antoci, C.; Gallati, M.; Sibilla, S. Numerical simulation of fluid–structure interaction by SPH. Comput. Struct. 2007, 85, 879–890. [Google Scholar] [CrossRef]
- Scolan, Y.M. Hydroelastic behaviour of a conical shell impacting on a quiescent-free surface of an incompressible liquid. J. Sound Vib. 2004, 277, 163–203. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).