A New Preliminary Model to Optimize PATs Location in a Water Distribution Network †
Abstract
:1. Introduction
2. Optimization Procedure
2.1. The Objective Function
2.2. The Mathematical Model
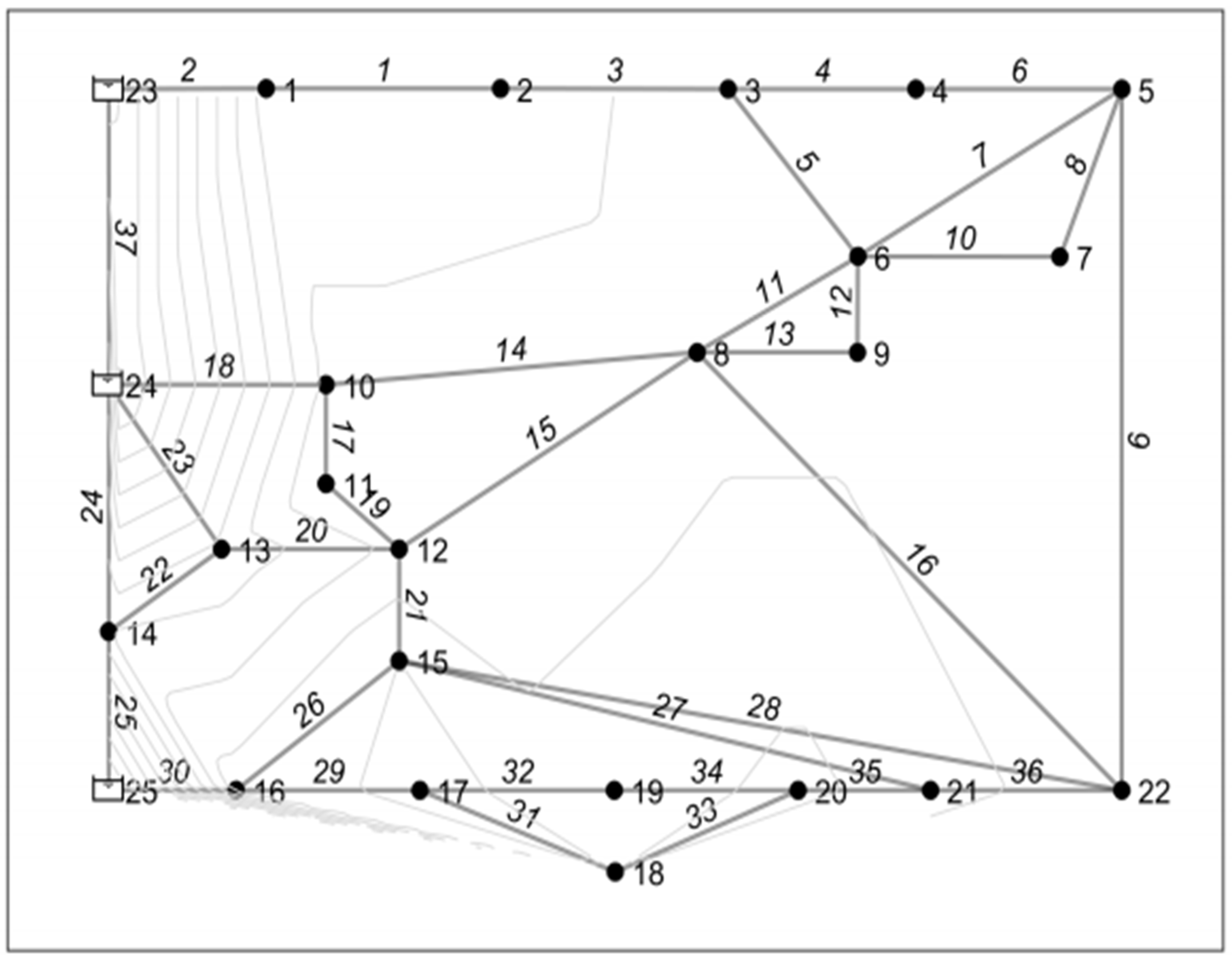
3. Preliminary Results
3.1. Preliminary Results in Average Condition
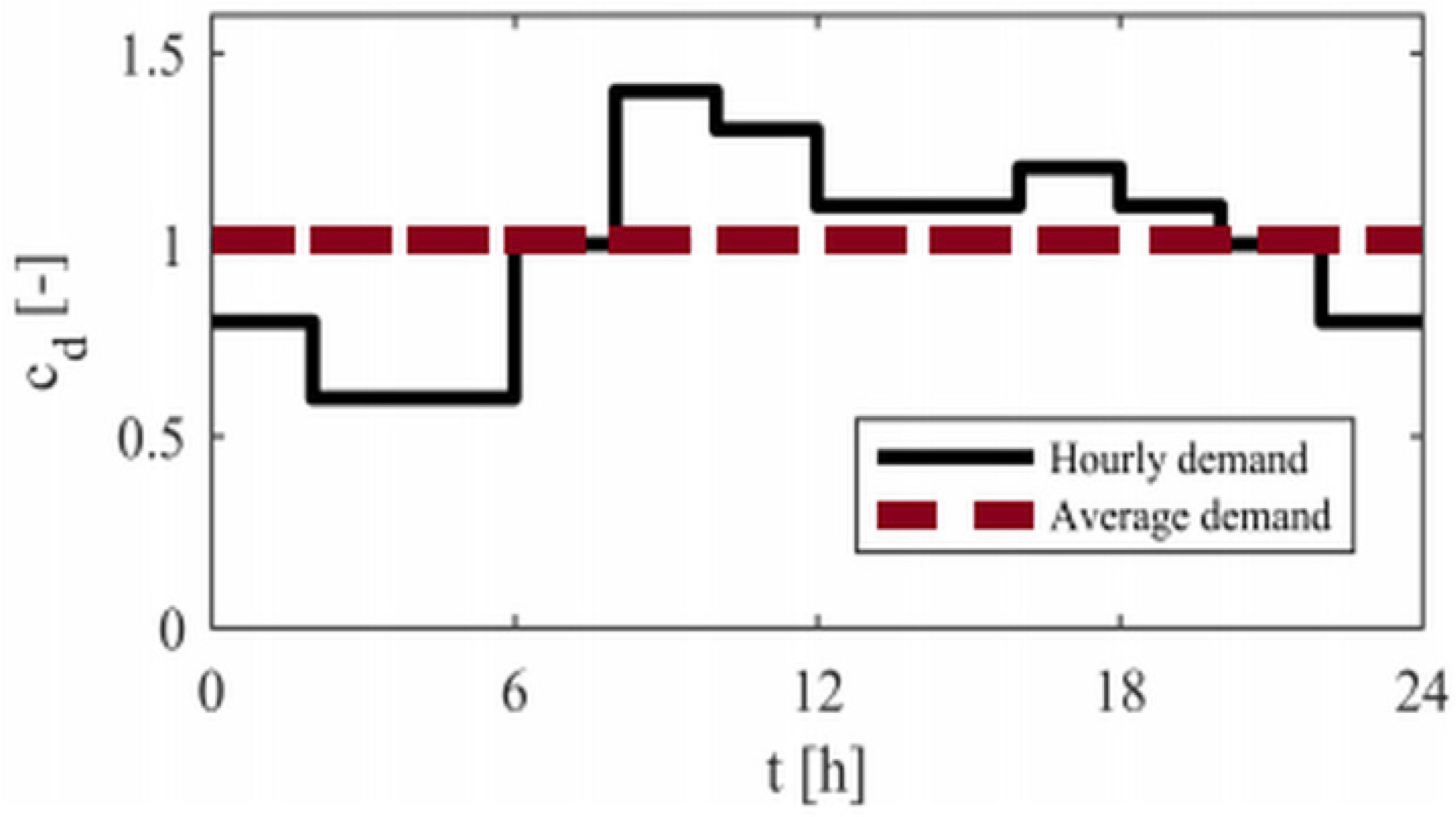
3.2. Preliminary Results in Daily Pattern Condition
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Energy recovery in existing water networks: Towards greater sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef]
- Colombo, A.F.; Karney, B.W. Energy and Costs of Leaky Pipes: Toward Comprehensive Picture. J. Water Resour. Plan. Manag. 2002, 128, 441–450. [Google Scholar] [CrossRef]
- Campisano, A.; Modica, C.; Vetrano, L. Calibration of Proportional Controllers for the RTC of Pressures to Reduce Leakage in Water Distribution Networks. J. Water Resour. Plan. Manag. 2012, 138, 377–384. [Google Scholar] [CrossRef]
- Schwaller, J.; van Zyl, J.E. Modeling the Pressure-Leakage Response of Water Distribution Systems Based on Individual Leak Behavior. J. Hydraul. Eng. 2014, 141, 1–8. [Google Scholar] [CrossRef]
- Fiuzat, A.A.; Akerkar, B.P. Power outputs of two stages of cross-flow turbine. J. Energy Eng. 1991, 117, 57–70. [Google Scholar] [CrossRef]
- Sammartano, V.; Sinagra, M.; Filianoti, P.; Tucciarelli, T. A Banki–Michell turbine for in-line water supply systems. J. Hydraul. Res. 2017, 55, 686–694. [Google Scholar] [CrossRef]
- Carravetta, A.; Derakhshan Houreh, S.; Ramos, H.M. Pumps as Turbines: Fundamentals and Applications; Springer: Cham, Switzerland, 2018; pp. 3–26. ISBN 978-3-319-67506-0. [Google Scholar]
- Gómez, E.; Cabrera, E.; Balaguer, M.; Soriano, J. Direct and indirect water supply: An energy assessment. Procedia Eng. 2015, 119, 1088–1097. [Google Scholar] [CrossRef]
- Carravetta, A.; Conte, M.C.; Antipodi, L. Energy efficiency index for water supply systems. In Proceedings of the 2015 AEIT International Annual Conference (AEIT), Naples, Italy, 14–16 October 2015; pp. 1–4. [Google Scholar]
- Giugni, M.; Fontana, N.; Ranucci, A. Optimal Location of PRVs and Turbines in Water Distribution Systems. J. Water Resour. Plan. Manag. 2014, 140, 6014004. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Ramos, H.M. A new low-cost installation scheme of PATs for pico-hydropower to recover energy in residential areas. Renew. Energy 2018, 125, 1003–1014. [Google Scholar] [CrossRef]
- Morani, M.C.; Carravetta, A.; Del Giudice, G.; McNabola, A.; Fecarotta, O. A Comparison of Energy Recovery by PATs against Direct Variable Speed Pumping in Water Distribution Networks. Fluids 2018, 3, 41. [Google Scholar] [CrossRef]
- Fecarotta, O.; Aricò, C.; Carravetta, A.; Martino, R.; Ramos, H.M. Hydropower Potential in Water Distribution Networks: Pressure Control by PATs. Water Resour. Manag. 2015, 29, 699–714. [Google Scholar] [CrossRef]
- Pugliese, F.; De Paola, F.; Fontana, N.; Giugni, M.; Marini, G. Experimental characterization of two Pumps As Turbines for hydropower generation. Renew. Energy 2016, 99, 180–187. [Google Scholar] [CrossRef]
- Pugliese, F.; De Paola, F.; Fontana, N.; Giugni, M.; Marini, G. Performance of vertical-axis pumps as turbines. J. Hydraul. Res. 2018, 56, 482–493. [Google Scholar] [CrossRef]
- Fecarotta, O.; Ramos, H.M.; Derakhshan, S.; Del Giudice, G.; Carravetta, A. Fine Tuning a PAT Hydropower Plant in a Water Supply Network to Improve System Effectiveness. J. Water Resour. Plan. Manag. 2018, 144, 04018038. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. Pump as turbine (PAT) design in water distribution network by system effectiveness. Water 2013, 5, 1211–1225. [Google Scholar] [CrossRef]
- Samora, I.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Simulated Annealing in Optimization of Energy Production in a Water Supply Network. Water Resour. Manag. 2016, 30, 1533–1547. [Google Scholar] [CrossRef]
- Tricarico, C.; Morley, M.S.; Gargano, R.; Kapelan, Z.; Savić, D.; Santopietro, S.; Granata, F.; de Marinis, G. Optimal energy recovery by means of pumps as turbines (PATs) for improved WDS management. Water Sci. Technol. Water Supply 2018, 18, 1365–1374. [Google Scholar] [CrossRef]
- Fecarotta, O.; McNabola, A. Optimal Location of Pump as Turbines (PATs) in Water Distribution Networks to Recover Energy and Reduce Leakage. Water Resour. Manag. 2017, 31, 5043–5059. [Google Scholar] [CrossRef]
- Jowitt, P.W.; Xu, C. Optimal Valve Control in Water Distribution Networks. J. Water Resour. Plan. Manag. 1990, 116, 455–472. [Google Scholar] [CrossRef]
- Araujo, L.S.; Ramos, H.M.; Coelho, S.T. Pressure Control for Leakage Minimisation inWater Distribution Systems Management. Water Resour. Manag. 2006, 20, 133–149. [Google Scholar] [CrossRef]
- Belotti, P.; Kirches, C.; Leyffer, S.; Linderoth, J.; Luedtke, J.; Mahajan, A. Mixed-integer nonlinear optimization. Acta Numer. 2013, 22, 1–131. [Google Scholar] [CrossRef]
| NPV [€] | No of PATs [-] | Average Power [kW] | Investment Cost [€] | Water Saving [m3/day] | DPPe [years] | |
|---|---|---|---|---|---|---|
| Proposed optimization | 778,495 | 9 | 12.04 | 29,199 | 859 | 3 |
| Fecarotta & McNabola (2017) | 833,740/ 830,679 | 16/6 | 14.53/14.06 | 50,396/50,293 | 929 | 4.7 |
| NPV [€] | No of PATs [-] | Average Power [kW] | Investment Cost [€] | Water Saving [m3/day] | DPPe [years] | |
|---|---|---|---|---|---|---|
| Proposed optimization | 781,891 | 6 | 10 | 20,647 | 797 | 2.3 |
| Fecarotta & McNabola (2017) | 790,320/ 783,992 | 20/6 | 13.43/12.63 | 62,556/62,256 | 901 | 6.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morani, M.C.; Carravetta, A.; D’Ambrosio, C.; Fecarotta, O. A New Preliminary Model to Optimize PATs Location in a Water Distribution Network. Environ. Sci. Proc. 2020, 2, 57. https://doi.org/10.3390/environsciproc2020002057
Morani MC, Carravetta A, D’Ambrosio C, Fecarotta O. A New Preliminary Model to Optimize PATs Location in a Water Distribution Network. Environmental Sciences Proceedings. 2020; 2(1):57. https://doi.org/10.3390/environsciproc2020002057
Chicago/Turabian StyleMorani, Maria Cristina, Armando Carravetta, Claudia D’Ambrosio, and Oreste Fecarotta. 2020. "A New Preliminary Model to Optimize PATs Location in a Water Distribution Network" Environmental Sciences Proceedings 2, no. 1: 57. https://doi.org/10.3390/environsciproc2020002057
APA StyleMorani, M. C., Carravetta, A., D’Ambrosio, C., & Fecarotta, O. (2020). A New Preliminary Model to Optimize PATs Location in a Water Distribution Network. Environmental Sciences Proceedings, 2(1), 57. https://doi.org/10.3390/environsciproc2020002057







