Total and Specific THMs’ Prediction Models in Drinking Water Pipe Networks ^†

Abstract

Although disinfection is a crucial process for the safety of drinking water, it is responsible for the formation of disinfection by-products (DBPs) being accused of severe health problems. The present study presents the development of models predicting trihalomethanes (THMs) in a drinking water supply system in Greece. Although some of the developed models can be used for the prediction of THMs, they are site-specific and cannot be used extensively.

1. Introduction

Disinfection is considered a particularly important process for drinking water safety, as it inactivates pathogenic micro-organisms protecting human health. Several outbreaks have been recorded in the past, due to many chemical and biological hazards in the drinking water supply chain. As disinfection is introduced in the drinking water process, waterborne diseases have been dramatically declined [1,2]. However, during the disinfection process, several disinfection by-products (DBPs) are formed. Two main groups of DBPs are known: trihalomethanes (THMs) and haloacetic acids (HAAs). THMs include chloroform (CM), bromodichloromethane (DCBM), dibromochloromethane (DBCM), and bromoform (BM) [3]. The first studies on DBPs appeared in the 1970s when Rook and others identified CM and other THMs in drinking water [3,4,5]. There are more than 600 DBPs reported and some of them are regulated while others are considered as emerging ones due to their lower occurrence level and effects [3,6]. THMs are formed mainly due to the reactions of chlorine with natural organic or inorganic matter. While DBPs formed are accused to be toxic and carcinogenic organic compounds, residual chlorine is crucial for the drinking water supply systems. Disinfection takes place normally in water reservoirs at the water supply network’s head and pathogens contaminate water as it travels along with the network and arrive at the consumers’ taps. Thus, the presence of residual chlorine is crucial. The present study presents the development of models predicting THMs (total, CM, BM, DCBM, DBCM) in a drinking water supply system in Greece. The models are data-driven, based on data gathered from the normal sampling procedures elaborated by the water utility. THMs predictive models are helpful to the water utility managers for decision making and can be used as a tool for the optimal selection of boosters to minimize DBPs formation and at the same time maintain the right disinfectant residual.

2. Literature Review on DBPs Predictive Models

DBPs predictive models’ development is a methodology increasingly recognized as it can be used by the water utility managers as a decision-making tool. For example, they can be used for setting the disinfection dose, the contact time, pH adjustment, etc. They are important because the aim is to reduce DBPs concentrations and at the same time maintain the required disinfectant residual [1]. The existence of such models in regions and water distribution networks (WDNs) with the same characteristics could be useful, as they provide sufficient estimations of DBP concentrations that could minimize the need for complicated and expensive analysis of such compounds. Boosters’ optimal locations and sampling optimal locations can be identified using such models.

The factors affecting the existence of DBPs are pH, chlorine dose, residual chlorine, temperature, contact time, the existence of organic materials, and seasonal variability [7,8]. While pH and temperature seem to be proportional to THMs concentrations, pH effects vary for different DBPs [9]. THMs concentrations vary throughout the water supply system, as higher concentrations are found in the network compared to the tanks [10]. This is probably due to the existence of biofilm formatted in pipes’ walls which reacts with the residual chlorine forming THMs.

Data-driven statistical models and process-based ones are found in the literature to predict DBPs formation. Data-driven models are mainly based on the statistical relationships of dependent and independent variables [11]. Process-based models are based on the actual processes taking place in the WDN [11]. Process-based models are more difficult to be developed as parameter estimation within a process-based model is imprecise or difficult to obtain [12] or the data required for the development of process-based models are not available [11] and the laws of chemistry and mathematics for the formation of DBPs should be known in advance [11,13]. Data availability is a crucial issue for the data-driven models but as more data become available, the statistical models are used more and more.

In previous studies, many DBPs prediction models have been developed and many of them are derived from linear and non-linear regression analysis. However, these models are site-specific and cannot be used widely. Some of these models have used laboratory data and other real field data. In Greece, only a few models have been developed for the Athens water supply system and water treatment plants [14,15,16], for river water in Lesvos island [17] and two water supply systems [1].

3. Materials and Methods

The present study uses real field data to develop models predicting total THMs and each of the four THMs, namely CM, BM, DCBM, DBCM. The data are taken from a water utility serving a city of about 55.000 people. The data are gathered during sampling processes followed by the water utility according to the Greek institutional framework. The samplings are taken from different points of the water distribution network. Chlorination takes place in the reservoirs, using sodium hypochlorite and the dose is determined by the water utility. The sampling frequency is based on the water quantity abstracted and the number of consumers served, according to the national legislation. The data gathered are variables measured by the water utility during check and audit monitoring processes. As the frequency of audit monitoring is lower than the check one, the number of available data is limited.

Statistical analysis is elaborated to develop the necessary models. Initially, the variables are tested for normality using the Kolmogorov–Smirnov (K–S) test to check the goodness-of-fit to the normal distribution [18] at significance level 0.05. The variables not following normal distribution are transformed. Then, the Pearson correlation matrix is used to examine the relationships between the variables. To perform a linear regression, the total trihalomethanes (TTHMs (or each one of THMs)) concentration (Y), is assumed to be a linear function of the inputs, X. The unknown parameters to be determined, a_i are the coefficients, as given in (1):

Y = a₀ + a₁ X₁ + a₂X₂ + … + a_nX_n

(1)

where n is the number of inputs used. The coefficients are chosen to minimize the sum of the squared differences between the predicted and actual values of Y. Multiple regression analysis is used to evaluate the statistically significant variables at a level of significance α. The models are tested using ANOVA tests to check if the residuals of the models follow the normal distribution [19], and the mean value of the residuals is zero. The residuals should be evenly attributed above and below zero, otherwise, it should be suspected a calculation error or that an additional variable should be added to the regression model [18]. To check autocorrelation, the Durbin Watson estimate is calculated. R² values are also gathered to check how well the model fits the data. Finally, the developed models are used for the validation of the results, comparing observed and predicted data.

4. Results and Discussion

The data gathered include pH, total organic carbon concentration TOC (mg/L), conductivity (µS/cm), residual chlorine (mg/L), turbidity (NTU), total THMs (µg/L) and the concentrations of the four THMs (chloroform—CM, bromoform—BM, bromodichloromethane—DCBM, and dibromochloromethane—DBCM) in µg/L. Water is abstracted from 27 different water boreholes. Data refer to a period of 5 years (2014–2018). TOC values range from 0.31 to 39.5 mg/L and TTHMs range from 0.48 to 68.35 µg/L, lower than the threshold. BM is 49.8% of the total TTHMs concentration, followed by DBCM (27.5%), while CM is only 6.27% of the total TTHMs concentration (Figure 1). Organic substances are not present in high concentrations in water as groundwater is abstracted. However, the existence of BM concentrations may indicate the presence of inorganic compounds such as Br⁻ mainly due to anthropogenic factors and of seawater intrusion.

Table 1. Total number, average, standard deviation, minimum and maximum values of the parameters.

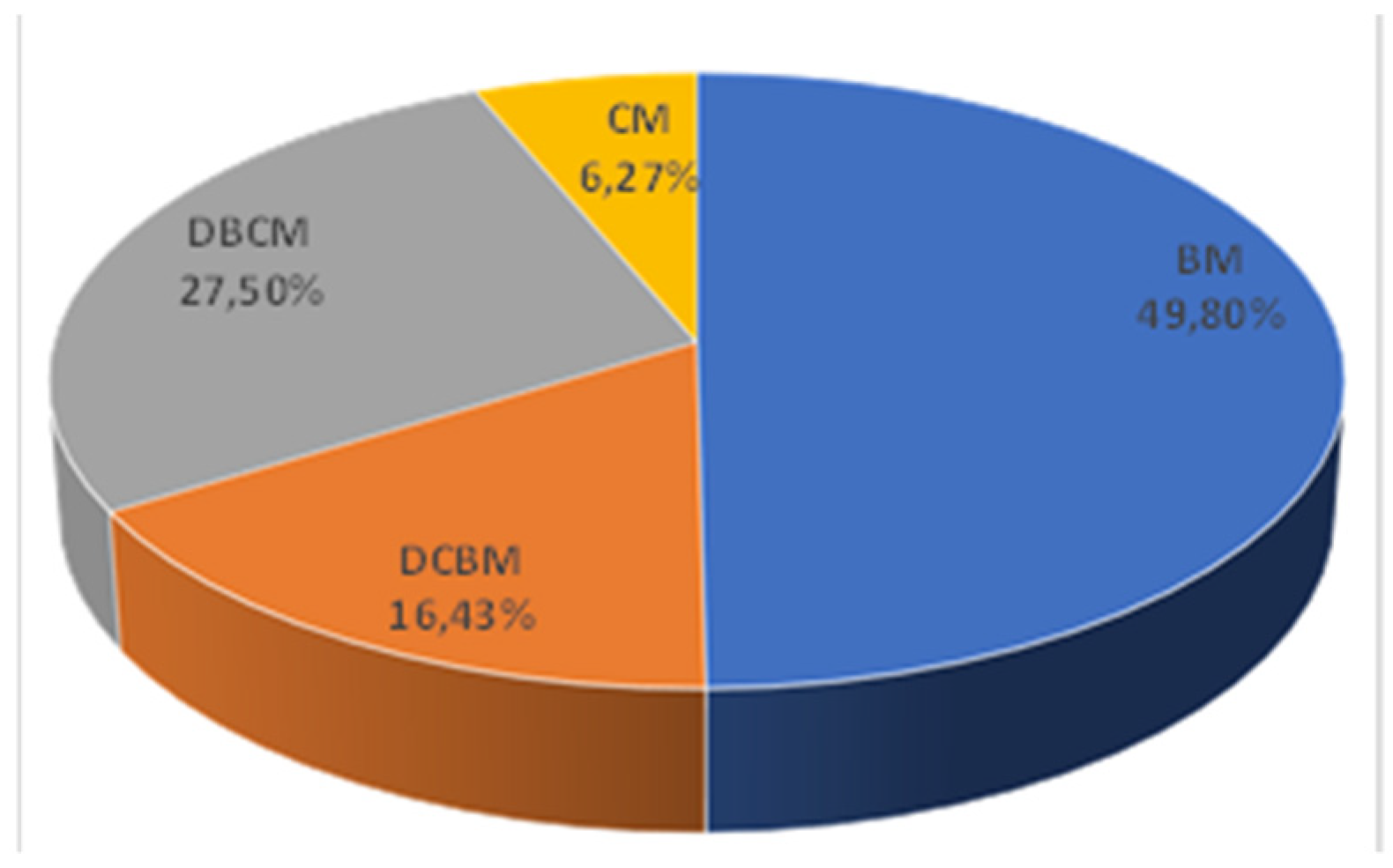
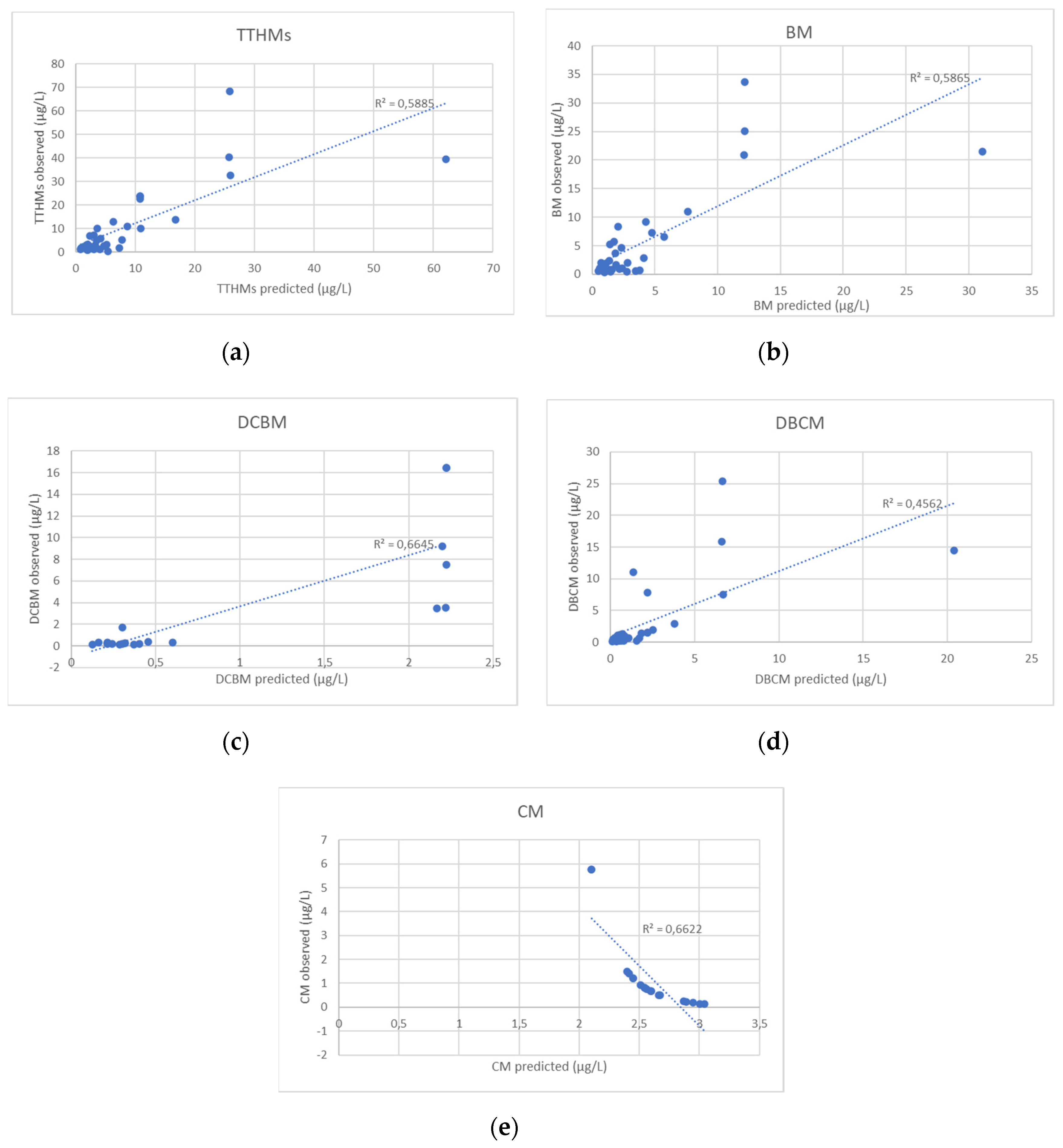
Parameter	N	AV	SD	MIN	MAX
pH	35	7.9314	0.3306	7.3	8.9
Conductivity	35	690.0	171.7	419.0	1141.0
Turbidity	35	0.2897	0.3964	0.10	2.45
TOC	35	5.01	9.94	0.31	39.5
Residual Chlorine	35	0.3417	0.1245	0.16	0.80
TTHMs	35	10.67	14.86	0.48	68.35
BM	33	5.64	8.14	0.35	33.73
DCBM	20	3.07	5.23	0.14	16.43
DBCM	33	3.115	5.735	0.12	25.43
CM	19	1.233	1.649	0.13	5.76

presents the total number of values (N), average (AV), standard deviation (SD), minimum (MIN), and maximum (MAX) values of the parameters studied.

The results of the K–S tests for the estimation of goodness-of-fit of the dependent variables of the model to the normal distribution showed that all dependent variables followed the normal distribution at significance level 0.05 except after log-transformation steps [17] and DCBM (

Table 2. Kolmogorov–Smirnov (K–S) values for the dependent and independent variables.

Parameter	K–S	Parameter	K–S	Parameter	K–S	Parameter	K–S
pH	0.104	Turbidity	0.364	DBCM	0.372	(DCBM)−0.6	0.179
Conductivity	0.150	TTHMs	0.249	CM	0.330	logDBCM	0.133
TOC	0.442	BM	0.258	logTTHMs	0.134	logCM	0.130
Residual Chlorine	0.178	DCBM	0.344	logBM	0.153	logturbidity	0.151
						(TOC)−2	0.160

). DCBM values were transformed using the Box-Cox transformation in Minitab. It was found that (DCBM)^−0.6 follows normal distribution at significance level 0.05. Independent variables were also tested for normality using the K–S test. Only pH, conductivity, and residual chlorine follow normal distribution at the 0.05 significance level. Thus, log-transformation for turbidity took place (Table 2). Regarding TOC another transformation took place using Box-Cox transformation. It was found that (TOC)⁻² follows normal distribution at significance level 0.05.

The relationships between the variables were examined by Pearson correlation matrix. Pearson correlation values show a strong positive correlation between TTHMs and BM, DCBM, DBCM, and CM concentrations which is logical as the 4 THMs form the total TTHMs (

Table 3. Pearson correlation values for the variables.

Parameter	TTHMs	pH	Cond.	TOC	Res. Chlor.	Turb.	BM	DCBM	DBCM
pH	0.497
Cond.	−0.446	−0.397
TOC	0.587	0.171	−0.338
Res. Chlor.	0.05	0.216	0.044	0.106
Turb.	0.249	−0.032	−0.023	0.570	−0.031
BM	0.958	0.580	−0.380	0.622	0.024	0.204
DCBM	0.566	−0.169	−0.416	0.857	0.023	0.229	0.759
DBCM	0.921	0.546	−0.456	0.349	−0.018	0.212	0.852	0.284
CM	0.906	−0.075	−0.327	0.968	0.120	0.200	−0.010	0.979	0.573

). TTHMs have a moderate positive correlation with TOC (r = 0.587), water pH (r = 0.497) and a moderate negative one with conductivity (r = −0.446) (Table 3). These findings are in accordance with previous studies. TOC values show a moderate positive correlation with turbidity (r = 0.570). BM values show a positive moderate correlation with water pH (r = 0.580) and TOC (r = 0.622). DCBM and CM values show strong positive correlations with TOC (r = 0.857 and r = 0.968) while DBCM values show a moderate one (r = 0.349). All four THMs show negative moderate correlations with conductivity (r ranging from −0.456 to −0.327) as shown in Table 3. Like BM, DCBM shows a moderate positive correlation with pH (r = 0.546) while DCBM and DBCM show a very low negative correlation.

Based on the data, multiple regression analysis was applied at significance level α = 0.05 for TTHMs, BM, DCBM, DBCM, and CM. Throughout the process of models’ development, several linear and non-linear regression analyses were performed. The inclusion of each variable in the proposed model was based on the t-criterion [20]. Methodological details about the model development are extensively discussed in past studies [1,15,21].

The first model predicts the TTHMs’ concentrations. All variables are initially used as independent variables (inputs). As the independent variables are not statistically significant (p > 0.05), they are excluded one-by-one from the model development process (

Table 4. Initial data from the multiple regression analysis for all models.

Term	Coef	t-Value	p-Value	Term	Coef	t-Value	p-Value	Term	Coef	t-Value	p-Value
logTTHMs model				logBM model				DCBM−0.6 model
Constant	−4.42	−2.42	0.022	Constant	−6.54	−3.29	0.003	Constant	1.42	0.32	0.754
pH	0.702	3.26	0.003	pH	0.913	3.88	0.001	pH	−0.171	−0.33	0.750
Conductivity	0.000281	0.67	0.507	Conductivity	0.000772	1.80	0.084	Conductivity	0.00132	0.96	0.353
TOC−2	−0.1026	−4.21	0.000	TOC−2	−0.0725	−2.60	0.015	TOC−2	0.2085	2.98	0.010
Res. Chl.	−0.212	−0.41	0.688	Res. Chl.	−0.429	−0.91	0.370	Res. Chl.	−2.12	−0.89	0.390
logTurbidity	0.152	0.57	0.576	logTurbidity	0.496	1.76	0.090	logTurbidity	−0.971	−1.46	0.167
logDBCM model				logCM model
Constant	−6.48	−3.27	0.003	Constant	0.11	0.04	0.968
pH	0.884	3.74	0.001	pH	0.182	0.57	0.580
Conductivity	0.00035	0.75	0.462	Conductivity	−0.00152	−1.69	0.115
TOC−2	−0.1112	−4.03	0.000	TOC−2	−0.08	−2.37	0.034
Res. Chl.	−0.240	−0.40	0.692	Res. Chl.	0.039	0.06	0.955
logTurbidity	0.296	1.02	0.318	logTurbidity	0.338	0.53	0.602

). Finally, only pH and TOC⁻² are found to be statistically significant (p < 0.05) (

Table 5. Statistical analysis data for the models developed.

Term	Coef	t-Value	p-Value	Model	R2	Durbin Watson
Constant	−3.84	−2.51	0.018	logTTHMs = −3.84 + 0.633 pH − 0.1056 TOC−2	61.61%	1.70419
pH	0.633	3.34	0.002
(TOC)−2	−0.1056	−5.30	0.000
Constant	−4.55	−2.49	0.019	logBM = −4.55 + 0.679 pH − 0.0923 TOC−2	53.64%	1.38332
pH	0.679	3.03	0.005
(TOC)−2	−0.0923	−3.69	0.001
Constant	0.619	2.49	0.023	DCBM−0.6 = 0.619 + 0.2749 TOC−2	64.27%	2.34693
(TOC)−2	0.2749	5.69	0.000
Constant	−5.89	−3.42	0.002	logDBCM = −5.89 + 0.809 pH − 0.118 TOC−2	65.95%	2.06195
pH	0.809	3.81	0.001
(TOC)−2	−0.118	−5.17	0.000
Constant	0.397	2.05	0.056	logCM = 0.397 − 0.0974 TOC−2	37.62%	2.16963
(TOC)−2	−0.0974	−3.20	0.005

). R² value is 61.61% for this model, which shows that it can be used in a satisfactory way for the prediction of TTHMs. All statistical analysis data are given in Table 5. Durbin Watson estimate provided in Table 5, is used to check autocorrelation. The values of the Durbin–Watson statistic were found to be 1.70419, showing that there is no autocorrelation. The model is

logTTHMs = −3.84 + 0.633 pH − 0.1056 TOC⁻²

(2)

The second model predicts BM concentrations. The independent variables found to be statistically significant (p < 0.05), after excluding the not statistically significant ones, are pH and TOC⁻² (Table 4 and Table 5). The value of R² is 53.64%, showing that the model provides a relatively good estimation for the prediction of BM concentrations (Table 5). Durbin Watson estimate is found to be 1.38332 and no autocorrelation exists. The model predicting BMs developed is

logBM = −4.55 + 0.679 pH − 0.0923 TOC⁻²

(3)

DCBM concentrations’ prediction model is then developed. Only TOC⁻² was found to be statistically significant (p < 0.05) (Table 4). The same methodology as before was used. The model provides a good estimation for the prediction of DCBM concentrations, as R² value is 64.27% (Table 5). No autocorrelation exists as Durbin Water estimate is found to be 2.3469. The model to predict DBCM concentrations is developed following the same methodology. The independent variables being statistically significant are pH and TOC⁻² (Table 4 and Table 5). The model can be used for the prediction of DBCM concentrations as it provides a very good estimation (R² = 65.95%). No autocorrelation exists as Durbin Water estimate is found to be 2.06195. The last model developed is the one predicting CM concentrations following the same methodology. Only TOC⁻² is found to be statistically significant (p < 0.05). As the R² value is 37.62%, the model does not provide a good model for the prediction of CM. The Durbin Watson estimate is 2.16963 showing that there is autocorrelation. The models developed are

DCBM^−0.6 = 0.619 + 0.2749 TOC⁻²

(4)

logDBCM = −5.89 + 0.809 pH − 0.1180 TOC⁻²

(5)

logCM = 0.397 − 0.0974 TOC⁻²

(6)

ANOVA tests are elaborated for all models. Statistical examination showed that the residuals of the models follow the normal distribution [19], and the mean value of the residuals is zero. In all cases, the analysis showed that the residuals are approaching normal distribution and the models are deemed valid to describe the experimental data (Figure 2a–e).

The developed models are used for the validation of the results. A comparison between predicted and observed values for all proposed models is presented in Figure 3a–e. For the model predicting total THMs, it can be observed that it does not provide a satisfactory estimation of the THMs concentrations formed, as only 8.57% of the predicted values range in the ±20% of observed values. For the models predicting BM, DCBM, and DBCM, only 12.12%, 25.0%, and 9.09% of the predicted values range in the ±20% of observed values. Finally, none of the predicted values with the model predicting CM range in the ±20% of observed values, showing that the model is not reliable. The regression coefficients (R²) are ranging from 0.4562 to 0.6622 (Figure 3a–e), which is a moderate satisfactory level of explanation of the observed variability.

All models can be used for the prediction of total THMs, BM, DCBM, DBCM concentrations, except for the one predicting CM concentration. This model is weaker than the others as the dataset used contains a smaller amount of variables’ values (19 compared to 33 for BM, DBCM, and 35 to TTHMs). Although the number of variables’ values used for the prediction of DCBM are also a small number (20), it seems that the model is adequately reliable. An important factor affecting the reliability of the developed models is that THMs concentrations are low as the sampling takes place in the reservoirs before the entrance of the water into the water distribution network, where possible reactions with the biofilm found in the pipes’ walls take place.

Comparing the models developed in this study with the models developed in other studies, it can be concluded that as pH increases, TTHMs, BM, DBCM concentrations increase. The data studied did not show a relationship between the concentrations of DCBM and CM with pH, probably because the dataset contains a small number of data. However, there are studies in the literature showing that the effect of pH varies on TTHMs formation [9]. The models developed show that as TOC concentrations increase, THMs values increase for all models. Such findings are in accordance with the findings from the literature [9].

Other explanatory variables such as disinfectant dose, reaction time, temperature, and others are not available in this study. The availability of reliable data is an issue mentioned in many studies affecting the choice of explanatory variables. All data are from samples taken in autumn. Studies have shown that higher THMs levels exist in the summer months. In the present study, it must be noted that the model is site-specific and cannot be used extensively. A limitation of the study is that the models are validated with the same dataset.

5. Conclusions

The present study uses real field data to develop total THMs models and models predicting each of the four THMs, namely CM, BM, DCBM, DBCM. The data are taken from a water utility serving a city of about 55.000 people. The data are gathered during sampling processes followed by the water utility according to the Greek institutional framework. The samplings are taken from different points of the water supply network. The paper: (a) investigates the formation of THMs during chlorination of groundwaters taking into consideration the available variables such as pH and TOC; (b) develops predictive models for the concentrations of total THMs, BM, DCBM, DBCM, and CM formed during chlorination of these groundwaters; and (c) statistically evaluates the developed models, in comparison to the models developed during previous studies for THMs [15,21] using the same modeling technique (multiple regression).

The study’s results showed that models developed to predict the formation of total THMs, BM, DCBM, and DBCM are reliable and can be used. However, the model developed for CM prediction is not reliable. Reasons for that include the lack of enough data and lack of data for explanatory variables affecting the formation of THMs. Finally, as all samplings are done in autumn, it is suggested that seasonal variation should be taken into consideration elaborating more samplings all over the year, to study the effect of the season in the formation of TTHMs, which is found to be related in other studies [15].

As the formation reactions of DBPs are complex, universally applicable models are difficult to be developed. The models developed can be used in regions and WDNs with the same characteristics. These models are useful for the water utility managers during the decision making for the disinfection dose, the pH adjustment, etc. Additionally, such models can be used to locate the optimal locations for chlorination boosters to achieve the desired chlorination and the right residual chlorine levels, without forming high THMs concentrations. Finally, these models in combination with the residual disinfectant ones can result in the optimal selection of sampling points for water quality control to be used for epidemiological studies and health risk assessment [9,22,23].