An Alternative Concentration Estimator for Backward Lagrangian Stochastic Dispersion Models
Abstract
1. Introduction
2. Methods and Materials
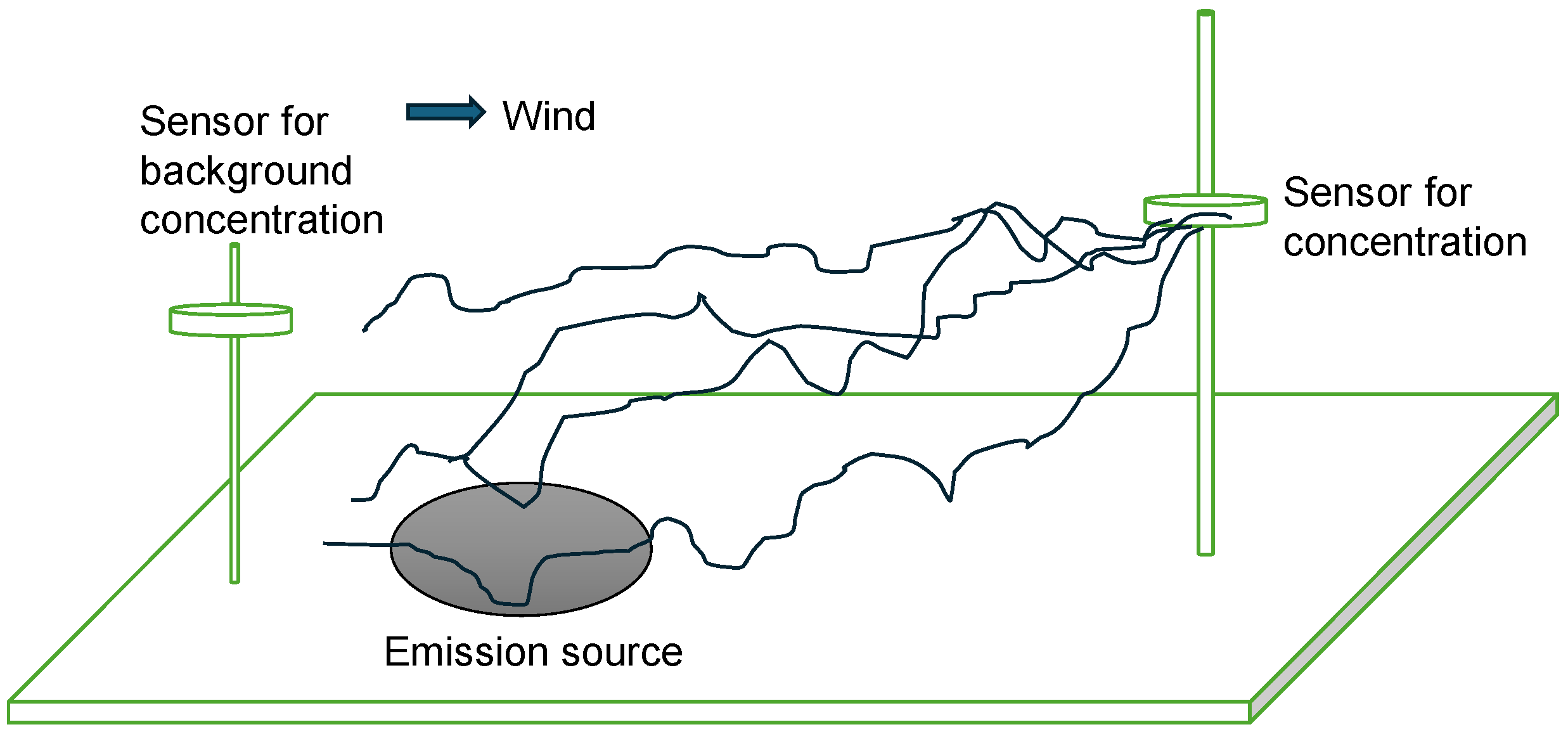
2.1. LS Models and the FWY Concentration Estimator
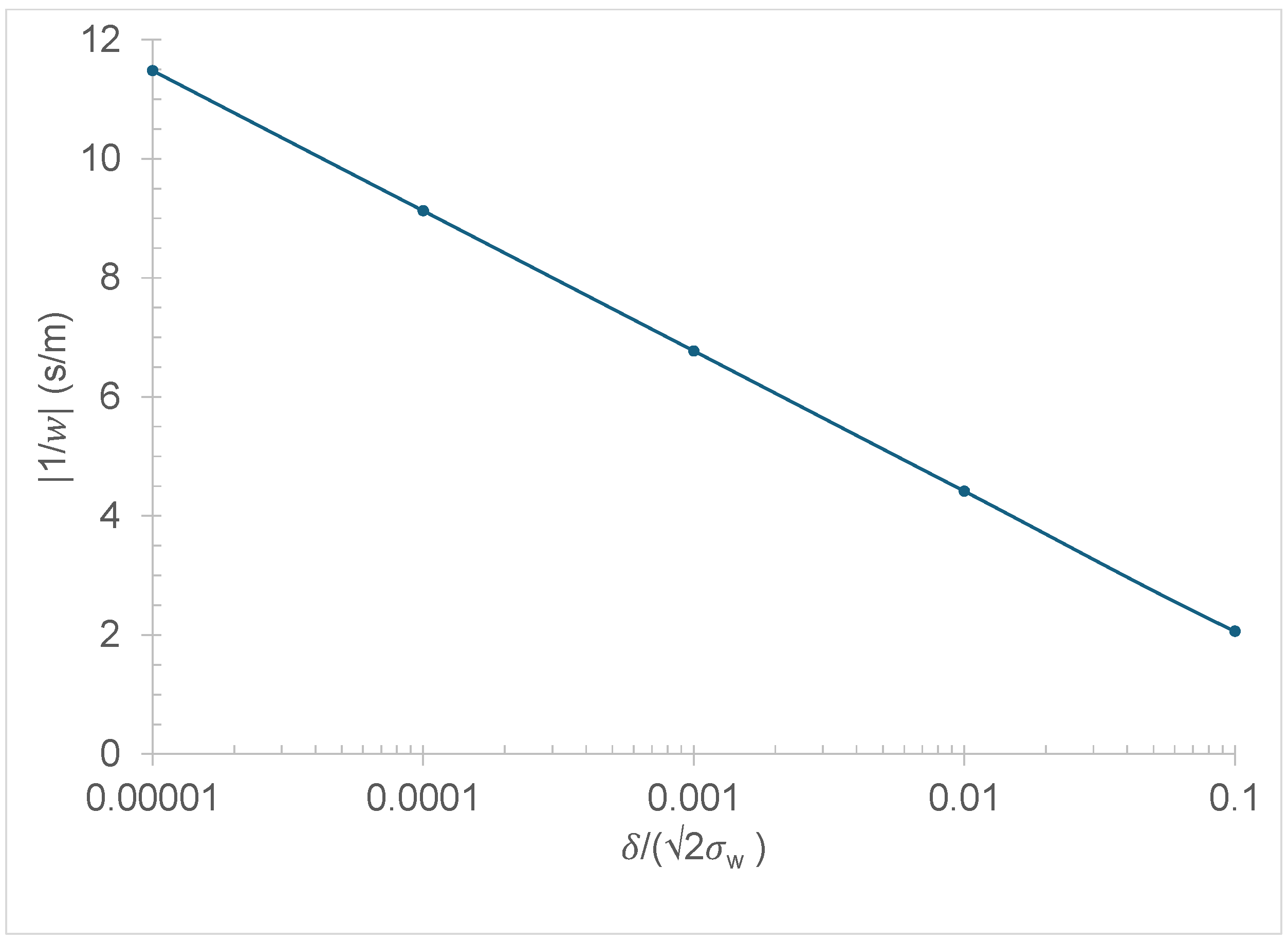
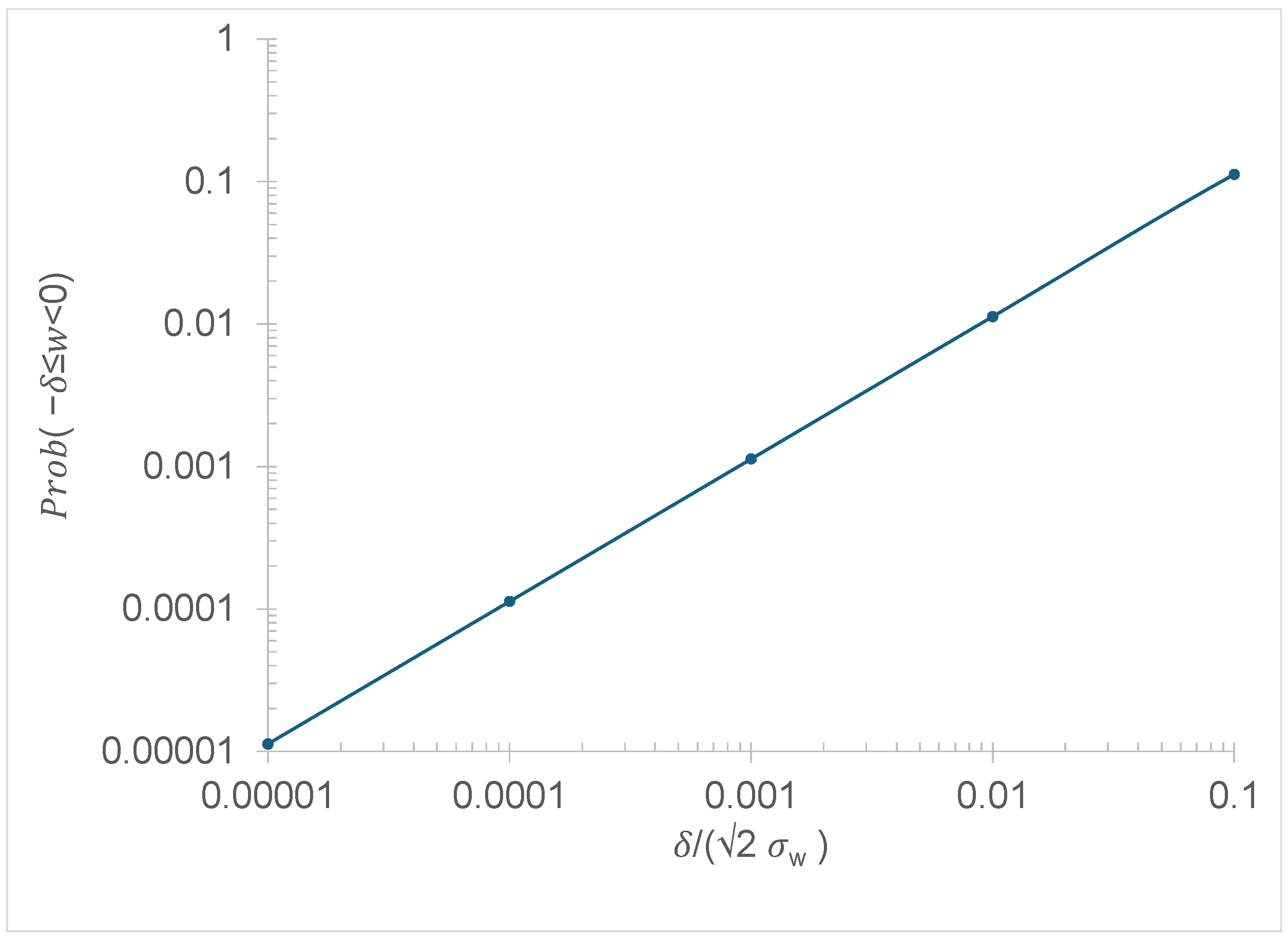
2.2. A Closer Examination of the FWY Concentration Estimator
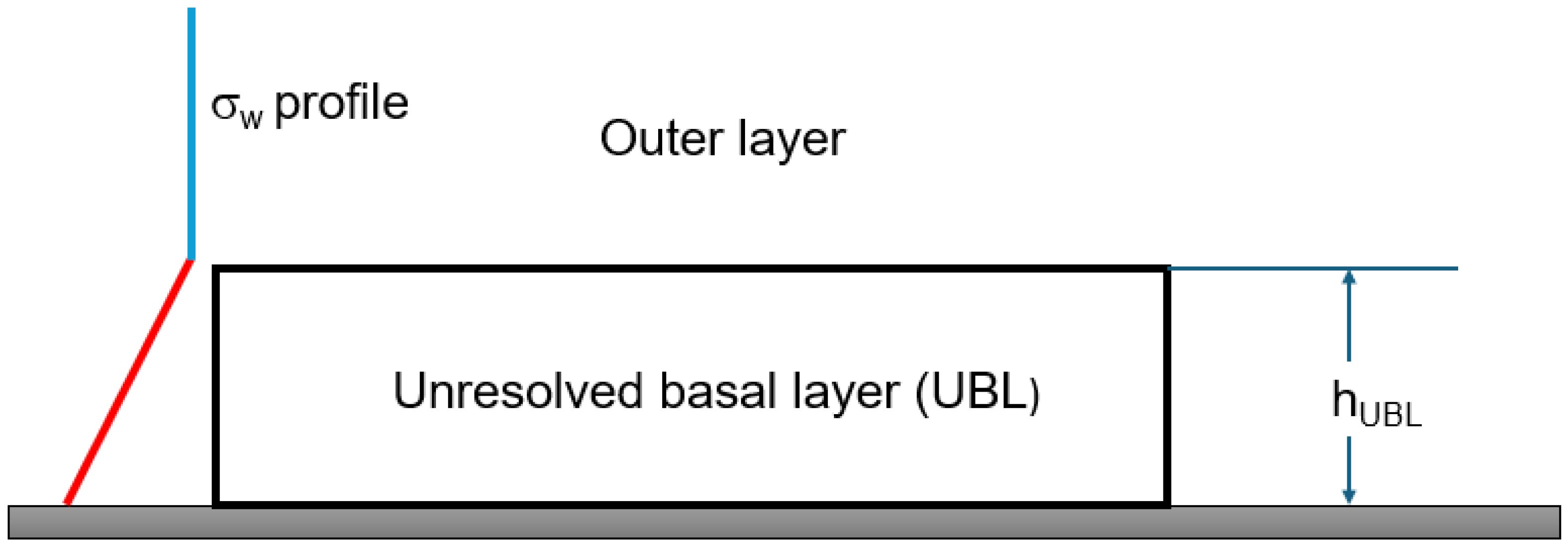
2.3. An Alternative Concentration Estimator
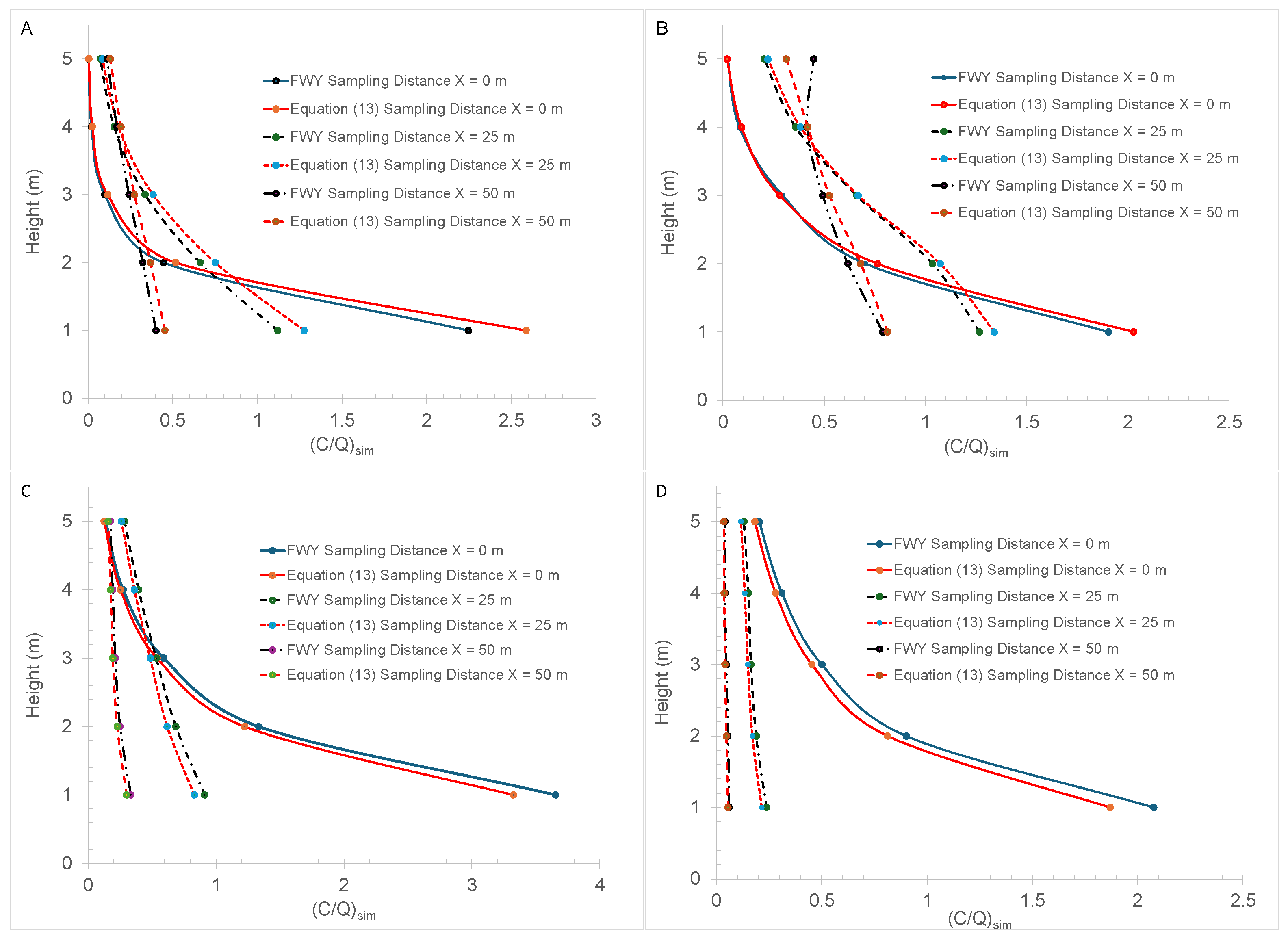
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description |
| A | relative frequency of occurrence of the updrafts (unitless) |
| B | relative frequency of occurrence of the downdrafts (unitless) |
| ck | concentration possessed by the kth particle hitting the emission source (in g/m3) |
| concentration obtained with the assumed emission rate, Qsim (in g m−3) | |
| C0 | Lagrangian velocity structure function constant (unitless) |
| E | emission rate from the entire area source (in g/s) |
| hUBL | height of the unresolved basal layer (in m) |
| L | Monin–Obukhov length (in m) |
| M | number of particles that hit the source in backward flights (dimensionless) |
| N | number of particles released at each receptor in a run (dimensionless) |
| p(w) | probability density function of vertical velocity (in m−1 s) |
| (w) | probability density function of vertical velocity in updrafts (in m−1 s) |
| (w) | probability density function of vertical velocity in downdrafts (in m−1 s) |
| emission rate from a ground-level source (in g m−2 s−1) | |
| assumed emission rate in Lagrangian modeling (in g m−2 s−1) | |
| S | area of the ground-level source (in m2) |
| u* | friction velocity (in m s−1) |
| U | average wind speed (in m s−1) |
| w* | convective velocity scale (in m s−1) |
| the mean vertical velocity in updrafts (in m s−1) | |
| the negative mean vertical velocity in downdrafts (in m s−1) | |
| the variance of vertical velocity (=) (in m2 s−2) | |
| the third-order moment of vertical velocity (in m3 s−3) | |
| w0 | touchdown velocity of tracer particle on the source area (in m s−1) |
| defined as (in m s−1) | |
| Zi | depth of mixed layer under convective conditions (in m) |
| the standard deviation of vertical velocity in updrafts (in m s−1) | |
| the standard deviation of vertical velocity in downdrafts (in m s−1) | |
| the standard deviation of streamwise turbulent velocity in downdrafts (in m s−1) | |
| the standard deviation of lateral turbulent velocity in downdrafts (in m s−1) | |
| the standard deviation of vertical turbulent velocity in downdrafts (in m s−1) | |
| ε | the average dissipation rate of turbulent kinetic energy (in m2 s−3) |
Appendix A. Equations of Lagrangian Stochastic Models
References
- Wilson, J.D.; Thurtell, G.W.; Kidd, G.E. Numerical simulation of particle trajectories in inhomogeneous turbulence, III: Comparison of predictions with experimental data for the atmospheric surface layer. Bound.-Layer Meteorol. 1981, 21, 443–463. [Google Scholar] [CrossRef]
- Legg, B.J.; Raupach, M.R. Markov-chain simulation of particle dispersion in inhomogeneous flows: The mean drift velocity induced by a gradient in Eulerian velocity variance. Bound.-Layer Meteorol. 1982, 24, 3–13. [Google Scholar] [CrossRef]
- Thomson, D.J. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 1987, 180, 529–556. [Google Scholar] [CrossRef]
- Pope, S.B. Consistency conditions for random-walk models of turbulent dispersion. Phys. Fluids 1987, 30, 2374–2379. [Google Scholar] [CrossRef]
- Wilson, J.D.; Sawford, B.L. Review of Lagrangian stochastic models for trajectories in the turbulent atmosphere. Bound.-Layer Meteorol. 1996, 78, 191–210. [Google Scholar] [CrossRef]
- Lin, J.; Brunner, D.; Gerbig, C.; Stohl, A.; Luhar, A.; Webley, P. (Eds.) Lagrangian Modeling of the Atmosphere; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Hurley, P.J.; Physick, W.L.; Luhar, A.K. TAPM: A practical approach to prognostic meteorological and air pollution modelling. Environ. Model. Softw. 2005, 20, 737–752. [Google Scholar] [CrossRef]
- Gariazzo, C.; Papaleo, V.; Pelliccioni, A.; Calori, G.; Radice, P.; Tinarelli, G. Application of a Lagrangian particle model to assess the impact of harbour, industrial and urban activities on air quality in the Taranto area, Italy. Atmos. Environ. 2007, 41, 6432–6444. [Google Scholar] [CrossRef]
- Yee, E. Theory for reconstruction of an unknown number of contaminant sources using probabilistic inference. Bound.-Layer Meteorol. 2008, 127, 359–394. [Google Scholar] [CrossRef]
- Stein, A.F.; Draxler, R.R.; Rolph, G.D.; Stunder, B.J.B.; Cohen, M.D.; Ngan, F. NOAA’s HYSPLIT atmospheric transport and dispersion modeling system. Bull. Am. Meteorol. Soc. 2015, 96, 2059–2077. [Google Scholar] [CrossRef]
- Flesch, T.K.; Wilson, J.D.; Harper, L.A.; Crenna, B.P.; Sharpe, R.R. Sharpe, Deducing Ground-to-Air Emissions from Observed Trace Gas Concentrations: A Field Trial. J. Appl. Meteorol. Climatol. 2004, 43, 487–502. [Google Scholar] [CrossRef]
- Flesch, T.; Wilson, J.; Harper, L.; Crenna, B. Estimating gas emission from a farm using an inverse-dispersion technique. Atmos. Environ. 2005, 39, 4863–4874. [Google Scholar] [CrossRef]
- Prajapati, P.; Santos, E.A. Comparing methane emissions estimated using a backward-Lagrangian stochastic model and the eddy covariance technique in a beef cattle feedlot. Agric. For. Meteorol. 2018, 256, 482–491. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Wilson, K.B. Modeling CO2 and water vapor exchange of a temperate broadleaved forest across hourly to decadal time scales. Ecol. Model. 2001, 142, 155–184. [Google Scholar] [CrossRef]
- Woodward, F.I.; Lomas, M.R. Vegetation dynamics–simulating responses to climatic change. Biol. Rev. 2004, 79, 643–670. [Google Scholar] [CrossRef]
- Wysocka-Czubaszek, A.; Czubaszek, R.; Roj-Rojewski, S.; Banaszuk, P. Methane and nitrous oxide emissions from agriculture on a regional scale. J. Ecol. Eng. 2018, 19, 206–217. [Google Scholar] [CrossRef]
- Mikkelsen, R. Ammonia emissions from agricultural operations: Fertilizer. Better Crops 2009, 93, 9–11. [Google Scholar]
- Flesch, T.K.; Wilson, J.D.; Yee, E. Backward-time Lagrangian stochastic dispersion models, and their application to estimate gaseous emissions. J. Appl. Meteorol. 1995, 34, 1320–1332. [Google Scholar] [CrossRef]
- Loubet, B.; Milford, C.; Sutton, M.A.; Cellier, P. Investigation of the interaction between sources and sinks of atmospheric ammonia in an upland landscape using a simplified dispersion-exchange model. J. Geophys. Res. Atmos. 2001, 106, 24183–24195. [Google Scholar] [CrossRef]
- McBain, M.; Desjardins, R. The evaluation of a backward Lagrangian stochastic (bLS) model to estimate greenhouse gas emissions from agricultural sources using a synthetic tracer source. Agric. For. Meteorol. 2005, 135, 61–72. [Google Scholar] [CrossRef]
- Denmead, O.T. Approaches to measuring fluxes of methane and nitrous oxide between landscapes and the atmosphere. Plant Soil 2008, 309, 5–24. [Google Scholar] [CrossRef]
- Ni, K.; Köster, J.R.; Seidel, A.; Pacholski, A. Field measurement of ammonia emissions after nitrogen fertilization—A comparison between micrometeorological and chamber methods. Eur. J. Agron. 2015, 71, 115–122. [Google Scholar] [CrossRef]
- Riva, C.; Orzi, V.; Carozzi, M.; Acutis, M.; Boccasile, G.; Lonati, S.; Tambone, F.; D’IMporzano, G.; Adani, F. Short-term experiments in using digestate products as substitutes for mineral (N) fertilizer: Agronomic performance, odours, and ammonia emission impacts. Sci. Total Environ. 2016, 547, 206–214. [Google Scholar] [CrossRef]
- Yang, W.; Zhu, A.; Zhang, J.; Zhang, X.; Che, W. Assessing the backward Lagrangian stochastic model for determining ammonia emissions using a synthetic source. Agric. For. Meteorol. 2016, 216, 13–19. [Google Scholar] [CrossRef]
- Lam, S.K.; Suter, H.; Davies, R.; Bai, M.; Mosier, A.R.; Sun, J.; Chen, D. Direct and indirect greenhouse gas emissions from two intensive vegetable farms applied with a nitrification inhibitor. Soil Biol. Biochem. 2018, 116, 48–51. [Google Scholar] [CrossRef]
- Shaw, J.T.; Allen, G.; Pitt, J.; Shah, A.; Wilde, S.; Stamford, L.; Fan, Z.; Ricketts, H.; Williams, P.I.; Bateson, P.; et al. Methane flux from flowback operations at a shale gas site. J. Air Waste Manag. Assoc. 2020, 70, 1324–1339. [Google Scholar] [CrossRef] [PubMed]
- Rodean, H.C. Stochastic Lagrangian Models of Turbulent Diffusion. Meteorol. Monogr. 1996, 26, 1–84. [Google Scholar] [CrossRef]
- Luhar, A.K.; Sawford, B.L. Lagrangian stochastic modeling of the coastal fumigation phenomenon. J. Appl. Meteorol. Climatol. 1995, 34, 2259–2277. [Google Scholar] [CrossRef]
- Wall, H.S. Analytic Theory of Continued Fractions; Chelsea Publishing Company: New York, NY, USA, 1948. [Google Scholar]
- Press, W.H.; Vetterling, W.T.; Teukolsky, S. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007; ISBN 978-0-521-88068-8. [Google Scholar]
- Wilson, J.D.; Flesch, T.K. Flow boundaries in random flight dispersion models: Enforcing the well-mixed condition. J. Appl. Meteorol. 1993, 32, 1695–1707. [Google Scholar] [CrossRef]
- Raupach, M.R.; Antonia, R.A.; Rajagopalan, S. Rough-Wall Turbulent Boundary Layers. Appl. Mech. Rev. 1991, 44, 1–25. [Google Scholar] [CrossRef]
- Bhaganagar, K.; Kim, J.; Coleman, G. Effect of roughness on wall-bounded turbulence. Flow Turbul. Combust. 2004, 72, 463–492. [Google Scholar] [CrossRef]
- Ismail, U.; Zaki, T.A.; Durbin, P.A. The effect of cube-roughened walls on the response of rough-to-smooth (RTS) turbulent channel flows. Int. J. Heat Fluid Flow 2018, 72, 174–185. [Google Scholar] [CrossRef]
- Ma, R.; Alamé, K.; Mahesh, K. Direct numerical simulation of turbulent channel flow over random rough surfaces. J. Fluid Mech. 2021, 908, A40. [Google Scholar] [CrossRef]
- Finnigan, J. Turbulence in plant canopies. Annu. Rev. Fluid Mech. 2000, 32, 519–571. [Google Scholar] [CrossRef]
- Nemitz, E.; Loubet, B.; Lehmann, B.E.; Cellier, P.; Neftel, A.; Jones, S.K.; Hensen, A.; Ihly, B.; Tarakanov, S.V.; Sutton, M.A. Turbulence characteristics in grassland canopies and implications for tracer transport. Biogeosciences 2009, 6, 1519–1537. [Google Scholar] [CrossRef]
- Baerentsen, J.H.; Berkowicz, R. Monte Carlo simulation of plume dispersion in the convective boundary layer. Atmos. Environ. 1984, 18, 701–712. [Google Scholar] [CrossRef]
- Luhar, A.K.; Britter, R.E. A random walk model for dispersion in inhomogeneous turbulence in a convective boundary layer. Atmos. Environ. 1989, 23, 1911–1924. [Google Scholar] [CrossRef]
- Du, S.; Wilson, J.D.; Yee, E. Probability density functions for velocity in the convective boundary layer, and implied trajectory models. Atmos. Environ. 1994, 28, 1211–1217. [Google Scholar] [CrossRef]
- Du, S. Universality of the Lagrangian velocity structure function constant (C0) across different kinds of turbulence. Bound.-Layer Meteorol. 1997, 83, 207–219. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Sun, C.; Wang, W.; Tu, X.; Du, S. An Alternative Concentration Estimator for Backward Lagrangian Stochastic Dispersion Models. Earth 2025, 6, 105. https://doi.org/10.3390/earth6030105
Wang B, Sun C, Wang W, Tu X, Du S. An Alternative Concentration Estimator for Backward Lagrangian Stochastic Dispersion Models. Earth. 2025; 6(3):105. https://doi.org/10.3390/earth6030105
Chicago/Turabian StyleWang, Biao, Caiping Sun, Wei Wang, Xingyue Tu, and Shuming Du. 2025. "An Alternative Concentration Estimator for Backward Lagrangian Stochastic Dispersion Models" Earth 6, no. 3: 105. https://doi.org/10.3390/earth6030105
APA StyleWang, B., Sun, C., Wang, W., Tu, X., & Du, S. (2025). An Alternative Concentration Estimator for Backward Lagrangian Stochastic Dispersion Models. Earth, 6(3), 105. https://doi.org/10.3390/earth6030105




