Abstract
The northern Yucatán Peninsula hosts a complex karstic environment shaped by carbonate platform development and the Chicxulub impact event, making subsurface characterization crucial for geological and hydrogeological studies. This work aimed to resolve the shallow crustal structure and identify major tectonic features that influence karst processes and groundwater dynamics. We applied a rapid 3D gravity inversion method, linear back projection (LBP), to Bouguer anomaly data, combined with Euler deconvolution to map shallow and deep fault systems. The inversion produced a high-resolution density model down to 12.8 km depth, revealing key geological structures. Multilevel thresholding delineated significant low-density basins, notably the Chicxulub crater, as well as buried sedimentary basins. Euler solutions identified fault networks that coincide with areas of intense karstification, particularly in the eastern peninsula. Results highlight the interplay between impact-related tectonics and karst evolution, influencing groundwater flow paths and recharge zones. This study demonstrates the effectiveness of gravity inversion and Euler deconvolution for regional crustal imaging in carbonate platforms and emphasizes the need for further local-scale surveys to investigate coastal aquifer vulnerability and saltwater intrusion processes.
1. Introduction
The Yucatán block was initially connected to the Louisiana–Texas block, but it was separated and displaced by the opening of the Gulf of Mexico. Eventually, it assumed its current position in the upper Triassic region, approximately 200 million years ago [1].
The Yucatán Peninsula, covering the states of Yucatán, Quintana Roo, and part of Campeche, is a large block-shaped landmass composed of a marine carbonate platform. It emerged above sea level around 26 million years ago during the Oligocene period. Physiographic features include the Sierrita de Ticul in the south, a range of hills with altitudes up to 250 m, dividing the region into hilly terrain to the south and a flat plain to the north. Surface drainage is minimal, with underground rivers that form a network of caves, cenotes, and flooded depressions called “aguadas”, with the Champoton River being an exception.
The shallow stratigraphy of the Yucatan Peninsula is composed of a sequence of marine calcareous rocks from the Cenozoic era. Quaternary rocks are visible along coastal areas [2,3,4,5]. The Peninsula exhibits limited outcrops of pre-Cenozoic sequences, posing a challenge for stratigraphic studies.
As mentioned earlier, the upper shelf, approximately 100 m thick, is composed of massive, recrystallized, cavernous limestones with high permeability. These layers overlay impermeable limestone formations with a thickness of several hundred meters in the northwestern part of the Peninsula [4,5]. Stratigraphic information has been derived primarily from the analysis and interpretation of drill-core and well-log data.
The Yucatán Peninsula is characterized by the absence of rivers and lakes, karstic development, shallow water tables, a peninsular aquifer system, and significant groundwater flow through dissolution structures [6].
Geophysical exploration surveys conducted by the PEMEX oil company documented notable gravity and magnetic anomalies in the northwestern portion of the peninsula, which were further investigated by drilling campaigns. These surveys initially revealed a large structure, corresponding to an impact crater formed approximately 66 million years ago [7,8]. The Chicxulub crater has a diameter of around 180 km and exhibits a complex multi-ring crater morphology. The crater was the result of the impact of an asteroid, approximately 10–15 km in diameter, on the marine platform in the southern Gulf of Mexico. This impact significantly disrupted life support systems, leading to the extinction of approximately 75 percent of Earth’s species.
Currently, the Chicxulub crater is found beneath a flat shelf of karstic origin, consisting of limestone, dolomites, and evaporites, with a thickness of approximately 300 to 1500 m [5,9,10]. In particular, there are no significant outcrops of impact-related units, including fragmented breccias or melted rocks. The relief and surface geology in the northwestern part of the peninsula reflect the impact structure’s influence, unveiling genetic links and correlations with the ring of cenotes, fracturing zones, and other semicircular depressions.
The main geomorphological and geological structures in the peninsula have been inferred from satellite and aerial images, as well as geophysical surveys and drilling programs. Various regional seismic surveys have been conducted offshore in the Yucatán shelf. However, the onshore portion has been primarily explored using potential field methods. This modeling technique has proven instrumental in visualizing topographic and morphological characteristics, identifying fault and fracturing patterns, and discerning karstic developments. These features are intricately linked to the subsidence/uplift and differential compaction of impact breccias and melted rocks, as well as other structural elements such as edges, rings, central uplift, and peak rings.
The origin and evolution of karst formations in the Yucatán Peninsula are not yet clearly established. It is likely that tectonic activity during the Neogene–Quaternary period and fluctuations in sea levels in the Quaternary are closely related to this geomorphological process [11,12,13,14].
The conclusion of the last global glaciation, marking the end of the Pleistocene, resulted in a sea level drop of approximately 110 m [15]. This glacial period ended around 18,000 years ago, and the subsequent rise in sea level led to flooding of broad coastal plains in the Atlantic Ocean, which is evident in the Florida and Yucatán platforms. Tectonic activity in the southern Yucatan Peninsula caused a tilting uplift, contributing to the formation of fracture systems oriented in north and northeast directions.
The geological record of the Yucatán Platform is intertwined with the opening of the Gulf of Mexico, which began in the Upper Triassic. During the Kimmeridgian, the Yucatan block shifted southeastward through a system of dextral faults that separated the Yucatan and Florida platforms. Clayey carbonate facies formed during the Tithonian. In the lower Cretaceous, limestone was deposited in shallow water over sand. A marine transgression occurred in Mexico between the middle and upper Cretaceous, resulting in the deposition of a thick carbonate layer. During the same time, a substantial evaporitic layer formed in the Yucatan block.
From the end of the Maastrichtian until the Early Eocene, the Laramide Orogeny took place. The Sierra Madre Oriental emerged on the continental margin of the Gulf of Mexico due to folding and faulting. Carbonates with minor amounts of evaporites were deposited on the Yucatán platform. Sea levels fluctuated several times from the Paleogene, giving rise to varying sedimentary facies.
The study area encompasses the Northern Yucatán Peninsula, using the Bouguer anomaly dataset presented in Figure 1, which is a slightly improved version of the map originally introduced by [16].
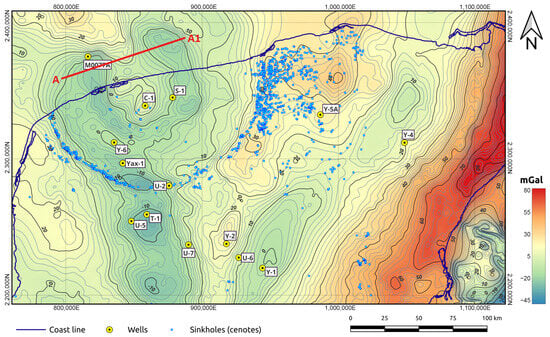
Figure 1.
Bouguer gravity map of the Yucatán Peninsula (after [16]) showing the seismic profile A–A1. Drilling sites are included and labeled with yellow circles. Major sinkholes (locally known as cenotes) are also included in blue circles. Yellow circles indicate the locations of exploratory boreholes.
To achieve these objectives, we used a combination of 3D gravity inversion using the linear back-projection (LBP) method and Euler deconvolution analysis applied to the Bouguer gravity anomaly data. These methodologies allow for the identification of subsurface density variations and fault systems, providing insights into the geological structure and tectonic evolution of the northern Yucatán Peninsula.
Several techniques have been developed to address inversion of potential field data, including iterative least-squares methods with Tikhonov regularization, Occam inversion strategies, stochastic optimization approaches such as genetic algorithms and simulated annealing, as well as joint inversion frameworks combining gravity and magnetic datasets. These methodologies offer detailed reconstructions of subsurface properties, but often require extensive computational resources, especially for large-scale regional studies. Given the extremely large size of the dataset analyzed in this work, we adopted the linear backprojection (LBP) method, which offers a computationally efficient alternative for rapid regional modeling, complemented by Euler deconvolution for fault system delineation.
The Yucatán Peninsula and the Chicxulub Crater
The Chicxulub crater, formed 66 million years ago by an impact of an asteroid on the Yucatán platform in the southern Gulf of Mexico [4,7,10,17,18,19,20,21], has a rim diameter of approximately 180 km, with its geometric center located at Chicxulub Puerto along the coastline. However, this area is covered by post-impact carbonate sediments, and there are no significant outcrops of impact lithologies. The continental portion of the crater rim exhibits a semicircular topographic depression and a fracture zone near the cenote ring.
The geomorphological and geological structures in the Yucatan Peninsula have undergone extensive study through satellite, aerial, geophysical, and geological investigations, as well as drilling programs. Various geophysical approaches, including seismic, magnetotelluric, ground-penetrating radar (GPR), and gravity surveys, have been employed to explore the Chicxulub crater. Drilling programs with continuous core recovery and geophysical well records have further contributed valuable insights. Core analyses have provided constraints on stratigraphy, petrophysical properties, mineralogy, geochemistry, and magnetic properties.
The main objective of this study is to improve the understanding of the shallow crustal structure of the northern Yucatán Peninsula, a region characterized by a complex interaction of impact-related tectonics, the development of the karst, and the evolution of the carbonate platform. Specifically, the study aims to (1) delineate sedimentary basins and tectonic discontinuities associated with the Chicxulub impact structure and regional fault systems, and (2) analyze the distribution of density contrasts that may reflect variations in lithology or structural uplift. By integrating 3D gravity inversion and Euler deconvolution techniques, we aim to construct a high-resolution model of the subsurface that highlights both vertical and lateral heterogeneities. The expected results include a geophysically constrained map of major fault trends and basin geometries, as well as a density model that may serve as a foundation for future hydrogeological or tectonic interpretations. Scientifically, this work contributes to a better understanding of how large-scale geological impacts and platform tectonics shape subsurface structures, particularly in karstified terrains with limited surface exposure. To further justify the use of gravity inversion and Euler deconvolution techniques in the present study, it is important to consider previous applications of these methods in similar geological contexts. Several studies have demonstrated the efficacy of these geophysical approaches in resolving buried structures such as impact craters, fault systems, and karst-related features beneath carbonate platforms. For instance, Reference [22] applied Euler deconvolution to image the subsurface geometry of the Serra da Cangalha impact structure in northeastern Brazil, revealing shallow circular faults and delineating the crater rim at depths consistent with other geophysical models. In the Yucatán Peninsula itself, Reference [16] employed gravity gradient analysis and cenote distribution mapping to constrain the size and structural expression of the Chicxulub impact crater, linking the cenote ring to a concentric fault system. A more recent and detailed 3D gravity inversion model of the Chicxulub crater by [23] integrated land and marine data, successfully reconstructing a multi-ring faulted structure and central uplift with high resolution. Furthermore, Reference [24] used modified Euler deconvolution and gravity data to investigate the Bangui anomaly in Central Africa, hypothesized to be a massive buried impact feature, thereby highlighting the value of these tools in contexts where direct geological observations are limited. These examples reinforce the methodological framework adopted in this study and underscore its potential to enhance our understanding of the buried tectonic and karstic systems of northern Yucatán.
In the initial stage, a fast single-step 3D inversion algorithm is applied to estimate a density distribution for the upper crustal region covering the entire northern Yucatán Peninsula. Linear back-projection (LBP) inversion, employed on Bouguer gravity data, is utilized to estimate a shallow crustal density model up to a depth of 12.8 km. Results demonstrate that LBP serves as an effective method for regional crustal imaging, offering a simple and efficient process with low computing costs. While LBP produces geologically meaningful density models, it is particularly advantageous for regional mapping, providing a faster alternative to more sophisticated inversion approaches.
Being a single-step inversion approach, LBP enables the modeling of large potential field datasets to obtain three-dimensional images of complex geological settings.
Additionally, Euler deconvolution in three dimensions is applied to the regional gravity data of the Yucatán Platform. The primary objective is to visualize both shallow and deep fault patterns in the study area. Euler deconvolution serves as a tool for processing and interpreting potential field data, allowing for the estimation of edges and depths of geologic features represented as anomalies in observed data.
Euler deconvolution in three dimensions facilitates imaging of the main gravity sources contributing to the Bouguer anomaly map in the study area. The spatial distribution of Euler solutions correlates with the primary faulting and fracturing patterns. To enhance interpretation, proper uncertainty bounds are introduced during the solution of Euler’s homogeneity equation. This approach yields a more interpretation-prone set of source locations with improved vertical resolution.
2. Materials and Methods
2.1. A Crustal Density Model of the Yucatán Peninsula
We consider the Bouguer anomaly dataset depicted in Figure 1 (adapted from [16]). We add some recently acquired gravity stations near the cenote ring to the original dataset. We have interpolated a regular grid comprising points from this map, resulting in the size of the observed gravity data, , being . Our objective is to estimate a crustal density model for the northern Yucatan Plateau, with the aim of imaging large-scale structural features related to significant geological processes in the area.
In addition to the general workflow shown in Figure 2, a complementary pseudocode is presented in Figure 3. This schematic representation condenses the core computational steps of the approach, including data pre-processing, gridding, inversion using LBP, and Euler deconvolution. It is intended to improve clarity and reproducibility by describing the algorithmic structure behind the proposed methodology.
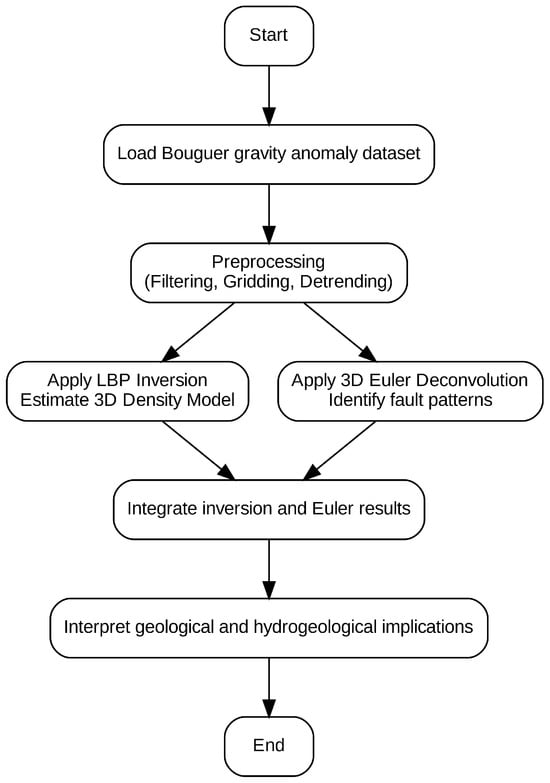
Figure 2.
Flowchart summarizing the methodology applied in this study, from data acquisition to geological interpretation.

Figure 3.
Pseudocode illustrating the general workflow for gravity data processing, inversion, and interpretation.
2.2. LBP Formulation
To introduce the formulation of the LBP method, we begin with a brief description of the linear inverse problem. Consider the relationship between the observed gravity data, , a linear model described by the sensitivity matrix, , and the model parameters, :
We aim to estimate a density model from the observed gravity data. To achieve this, we define an error function:
We find , which minimises . In this way, we find the least squares solution:
In the case of potential field data inversion, the term is ill-conditioned.
Following this straightforward strategy, we consider a first-degree approximation:
in which case we can estimate the model as follows:
The transposed matrix is the back-projection operator. In many fields of engineering, this method works qualitatively well. In order to minimize errors expressed in Equation (2), we introduce a scaling factor that allows us to minimize the mismatch between observed and computed data of the model. Use of a scaling factor is based on the assumption , where is a constant factor. We utilize this scaling factor to adjust the range of inverted densities and minimize the mismatch between theobserved and synthetic gravity data. In the case of large scale 3D gravity inversion, the term becomes a matrix of enormous dimensions and is generally ill-conditioned, as we mentioned before. The theoretical solution to the inverse problem is provided in (3).
However, directly computing is entirely infeasible in our case due to prohibitive memory and computational requirements. For our model, we discretize the subsurface into 701 × 401 × 128 = 35,980,928 prisms. With a Bouguer anomaly dataset comprising 281,101 measurements, the forward modeling matrix G would have dimensions 281,101 × 35,980,928, resulting in a matrix with more than 10 trillion elements. Direct computation of the inverse would involve the following:
- Memory required to store G: 40.44 TB.
- Memory required to store : 5.18 E (exabytes).
- Computational cost of forming : Approximately FLOPs (floating-point operations).
- Computational cost of inverting : On the order of FLOPs.
Even under optimistic conditions, using a high-end processor capable of 100 GFLOPs of sustained performance, the matrix inversion alone would take
In addition to time and memory bottlenecks, computing directly can introduce numerical instabilities if is rank-deficient or nearly singular, an issue often encountered in potential field inversions due to the undetermined nature of the problem. That is the reason we adopt the LBP approach to address these limitations and approximate the model solutions as shown in (5). This avoids the inversion of entirely and significantly reduces the following computational demands:
- Memory required for storing : 137.3 MB.
- Computational cost of : FLOPs.
- Estimated runtime for : ≈ 3.37 min on the same high-performance CPU.
Although LBP methods skips the term, we applied a scaling factor to compensate for the underestimation of the amplitude and to minimize the residuals between the observed and predicted gravity. This is a common strategy, where serves as a computationally inexpensive adjoint operator. From a practical standpoint, the LBP method offers multiple benefits including drastic reduction in memory footprint compared to storing , avoidance of numerical instability due to matrix singularity or rank deficiency, feasibility of real-time or high-resolution inversion using moderate computing resources, and the scability for very large 3D problems, as LBP scales linearly with the number of parameters and data points. While we acknowledge that LBP yields lower-resolution models and may introduce smoothing effects (i.e., “blurring”), it is a computationally viable strategy that allows the exploration of large-scale subsurface structures like those present in the Yucatán Peninsula. For these reasons, we intentionally did not pursue the explicit calculation of . The determination is grounded not in oversimplification, but in a careful evaluation of computational feasibility, numerical stability, and the size of the inversion domain. Thus, the adoption of LBP is justified not only by computational efficiency but also by its alignment with established practices for managing large-scale ill-conditioned inverse problems.
2.3. Synthetic Test LBP Inverse Model
To validate the reliability and resolution capability of the linear back-projection (LBP) method, we conducted a synthetic inversion test using a dense sphere embedded in a homogeneous background. The test model consisted of a 3D volume discretized into prisms. A spherical inclusion of radius 7 cells and density contrast of 1.0 was centered at coordinates (25, 25, and 10). Gravity data were simulated by vertically integrating the density model, adding Gaussian smoothing and a 5% noise level to mimic real-world acquisition conditions. The resulting gravity anomaly was inverted using the LBP operator (), and the recovered density model was compared to the original. The method successfully reproduced the primary features of the spherical body, demonstrating the ability of LBP to retrieve meaningful structural information despite the absence of full inverse computation. This confirms that, under suitable conditions, LBP can offer a computationally efficient approximation for large-scale gravity modeling. The test also supports the practical advantages of LBP, which were highlighted in previous sections, particularly in applications involving massive datasets where full inversion is computationally intractable. Figure 4 presents the true model, the simulated gravity anomaly, and the reconstructed density distribution obtained from the inversion.
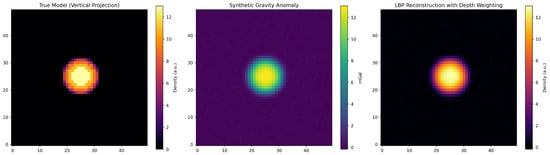
Figure 4.
Synthetic test illustrating the performance of the linear back-projection (LBP) method in gravity inversion. (Left) True 3D density model (vertical projection) of a high-density spherical anomaly embedded in a homogeneous medium. (Center) Synthetic Bouguer gravity anomaly generated from the model and smoothed using Gaussian filtering. (Right) LBP inversion result () with depth weighting. The recovered anomaly shows an expected degree of blurring, which is typical of LBP solutions when using low model discretization. However, increasing the number of prisms in the model grid enhances resolution and sharpness, confirming that LBP can provide geologically meaningful reconstructions under idealized conditions.
Given the approximate nature of the linear back-projection (LBP) method, which produces inherently blurred solutions by applying the adjoint operator to the data, finer discretization in the vertical direction was adopted to partially compensate for the loss of resolution. In this study, vertical prisms of 100 m were used, despite the coarser horizontal sampling dictated by the data spacing. This choice reflects a trade-off: while the inversion remains underdetermined, the enhanced vertical resolution allows for better delineation of structural trends and depth variations that would otherwise be smeared in the resulting model. The goal is not to obtain a precise quantitative reconstruction, but rather to generate a geologically meaningful image that captures the dominant features of the subsurface at the regional scale.
2.4. Euler Deconvolution of Gravity Data
We used Euler deconvolution [25,26,27] to estimate the depth to geologic sources that are expressed as anomalies in the observed gravity data. According to Euler’s theorem, is an homogeneous function of degree n, and t is a real number:
The degree of homogeneity, n, is directly related to the field associated with any specific type of source like point source, sphere, semi-infinite dike, contact, etc. [25]. The structural index is defined as .
According to Equation (7), the gravity field is caused by sources representing homogeneous functions in spatial coordinates [28]. Computing derivatives relative to the spatial coordinates in three dimensions, we have the following:
The unknowns are the coordinates of a point source from an observation point . corresponds to the observed anomaly within an estimated regional field, B, in addition to the rate of field decay with distance, . If observations are taken at , the system to be solved can be written as follows:
Equation (9) represents a system of linear algebraic equations, , where is a vector of unknown parameters. This overdetermined system can be solved by linear inversion, based on the procedure proposed by [25,29]: solving the system of equations formed by data in a moving window and accepting or rejecting solutions based on the quality of the estimates. In the Euler deconvolution analysis, a structural index (SI) value of 0 was selected. This choice corresponds to geological contacts or abrupt fault boundaries, which are consistent with the expected tectonic and karstic features in the study area. The SI = 0 setting allows for the detection of sharp lateral density contrasts associated with faulting and basin edges. Preliminary tests with higher values of the structural index (e.g., SI = 1, SI = 2) produced less coherent or overly diffuse source distributions, supporting the suitability of SI = 0 for this geological context. To evaluate the quality of the solutions, we considered the criteria of [25,29] related to vertical dispersion, accepting solutions whose standard deviation , in depth estimation , was less than or equal to a tolerance expressed as a percentage with respect to depth , as well as solutions whose depth was less than twice the window size. To account for lateral dispersion, solutions calculated outside a cone of influence centered on the moving window were rejected, as proposed by [28].
A drawback of this approach is the large number of remaining solutions, which can represent an issue in the context of non-uniqueness. For this work, we restricted solutions by involving a priori information, mainly on the structural index , employing the value corresponding with contacts and faults. Finally, the observation domain was scanned using overlapping square windows of 5 km and 20 km length per side, which allowed us to compute solutions with different maximum depths.
2.5. Synthetic Test of Euler Deconvolution
To evaluate the effectiveness of Euler deconvolution in resolving structural discontinuities, we constructed a synthetic 3D density model composed of two juxtaposed blocks with contrasting depths. This configuration mimics a normal fault system, providing a controlled scenario to test the spatial accuracy of the method. The dimensions of the model are km, discretized into uniform cells. A vertical fault offset of 5 km was introduced between the two density blocks, as can be seen in Figure 5, generating a gravity anomaly through forward modeling, subsequently processed via Euler deconvolution.
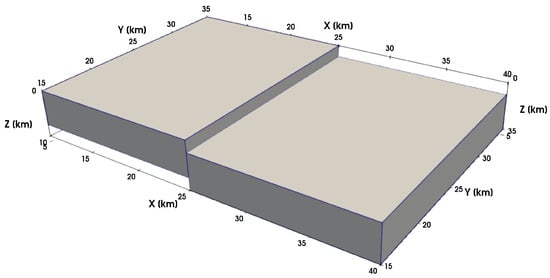
Figure 5.
Synthetic density model consisting of two blocks separated by a vertical fault with a 5 km throw. This configuration serves as a test case for evaluating Euler deconvolution performance in detecting sharp lateral density contrasts.
Euler solutions were computed using a structural index SI of 0, consistent with contacttype discontinuities, and filtered by vertical dispersion and solution quality. The recovered source locations show a well-constrained cluster of solutions along the fault plane, as shown in Figure 6, particularly at its lateral terminations and upper extents. Figure 7 shows the corresponding synthetic Bouguer anomaly map; this map displays a pair of gravity highs matching the denser block boundaries, which simulate abrupt lithological contrasts.
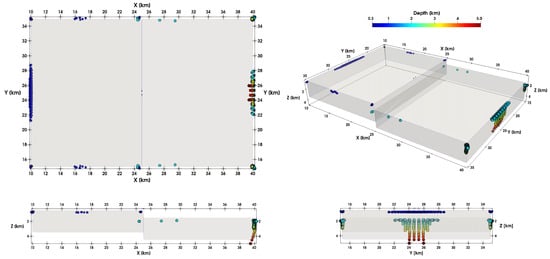
Figure 6.
Euler deconvolution solutions obtained from the synthetic anomaly. Solutions are colorcoded by depth and plotted in multiple views, showing strong clustering near the fault contact, with accurate vertical and lateral resolution.
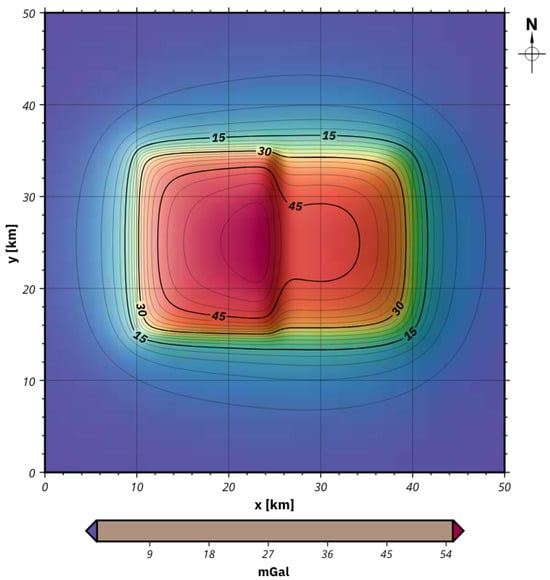
Figure 7.
Gravity anomaly produced by the faulted block model. The horizontal gradient of the field enhances the contrast near the contact, supporting the interpretability of Euler-derived solutions.
Visual inspection of the solution cloud in multiple perspectives (map view, 3D view, and cross-sections) confirms that Euler deconvolution effectively captures the geometry and depth of the causative structure. The highest-density clusters align with the edges of the block offset and reach depths of approximately 5 km, closely matching the true model configuration. This synthetic experiment demonstrates that, when properly tuned (e.g., structural index, window size, and quality thresholds), Euler deconvolution can reliably detect and estimate fault geometries and depths. Although the method is susceptible to noise and non-uniqueness in complex geological settings, its application to simplified models validates its use for identifying abrupt lateral density variations, such as those expected in the Yucatán Peninsula due to faulting and karst collapse. These results complement the 3D gravity inversion and reinforce the robustness of our joint interpretive framework.
3. Results
3.1. LBP Inversion
In Figure 8, we present the LBP inverted shallow crustal density model. Gravity imaging by LBP serves as a useful and efficient method for regional mapping, although it has limitations due to its relatively low spatial resolution compared to seismic methods, stemming from the natural ’soft field’ effect and ’ill-posed solution’ of potential field methods. Despite these limitations, three-dimensional LBP gravity imaging can generate extensive regional density models of geological significance.

Figure 8.
Three-dimensional shallow crustal density model of the Yucatán Peninsula, inverted using the linear back-projection (LBP) method applied to Bouguer gravity anomaly data. The model reveals major low-density basins and high-density structural features. Density values are expressed in g/cm3. Data are based on interpolated Bouguer anomaly maps with additional gravity stations near the cenote ring.
To address the wide range of density values produced by the LBP method, the density contrasts were linearly rescaled based on known density values from previous gravity models and measured samples [18,30,31,32,33]. The geological model reconstructed from applying LBP reveals significant structural features, with inflections indicating fault limits and small deviations associated with surface structures such as faults and cenotes, characteristic of the karstic topography of the region.
Multilevel thresholding was used to segment geobodies in the inverted density volume, successfully highlighting key structural features, including low-density basins, notably one associated with the Chicxulub crater. This basin is identifiable as a semicircular depression connected to the south by an enlarged ancient canyon-shaped valley, as illustrated in Figure 9.
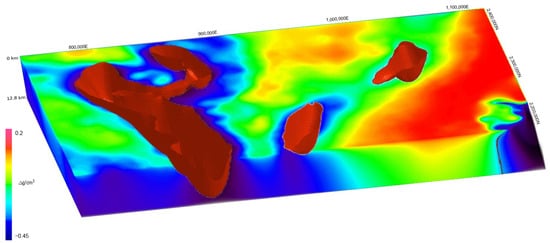
Figure 9.
Segmentation of low-density basins in the inverted density model using multilevel thresholding. The color scale represents density variations, with blue indicating lower densities and red indicating higher densities. This segmentation highlights major structural depressions, including the Chicxulub basin. Data are derived from the LBP-inverted shallow crustal density model.
Furthermore, the extraction of isosurfaces from the inverted shallow crustal density model using the LBP technique provides valuable information on the geological structure of the Yucatan Peninsula, particularly the Chicxulub crater, as depicted in Figure 10. By delineating the distribution of high-density materials within the crust, the LBP-derived model offers a detailed depiction of the subsurface landscape, shedding light on the formation mechanisms and evolutionary history of key geological features.
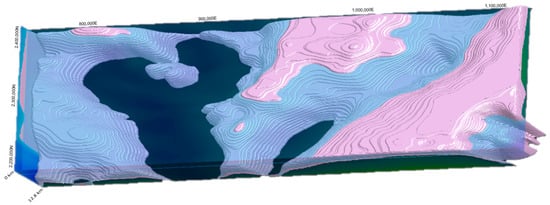
Figure 10.
Iso-surface configuration from the shallow crustal density model inverted by LBP. Highdensity rocks are preserved to enhance the geometry and location of three major basins, including the Chicxulub crater (see Figure 1).
To complement the gravity inversion results and provide further structural validation, we present a regional seismic profile crossing the Chicxulub crater, as shown in Figure 11. This profile illustrates significant crustal features, including central uplift, basin morphology, and post-impact stratigraphy, offering independent constraints on the shallow crustal model obtained from LBP gravity inversion. Specifically, the image corresponds to profile A–A1, a seismic transect located approximately 40 km from the center of the crater, running parallel to the coastline in the offshore region of the northwestern Yucatán Peninsula. The section was constructed using a full waveform inversion technique [33] and provides a high-resolution depiction of the crustal composition beneath the marine portion of the peninsula. In contrast, the crustal structure beneath the onshore area remains largely unknown, except at locations where deep boreholes have been drilled (see Figure 1). For this reason, gravity data are used in this study to investigate the crustal structure on land, acknowledging that the resolution of potential field methods is inherently lower than that of seismic reflection techniques.
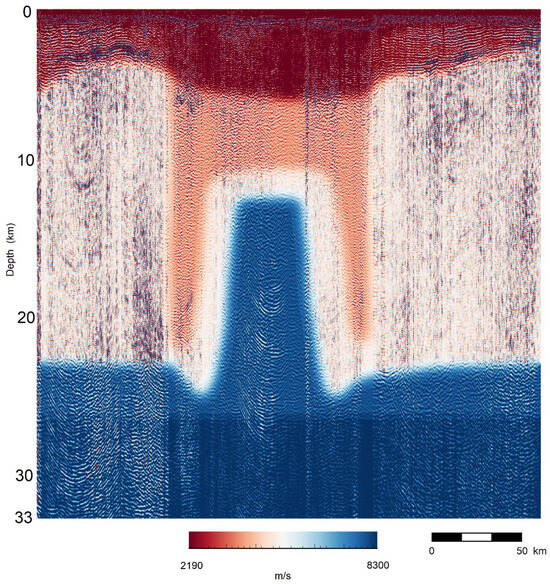
Figure 11.
A–A1 seismic profile across the Chicxulub crater area (modified from [33], see location in Figure 1) reveals the crustal structure down to 33 km depth. High-velocity contrasts delineate the central uplift and surrounding basins, showing good correlation in the upper region (dark red zone and below 12.8 km) with our gravity LBP inversion results.
3.2. Euler Deconvolution Solutions
Figure 12 presents the results of Euler deconvolution applied to the Bouguer gravity data set from the Yucatán Peninsula, integrating Euler solutions into a structural map depicting the distribution of geological faults and fractures. This map provides valuable information on the deformation styles and the tectonic stress regime of the area. Despite its tectonic stability, the Yucatán Peninsula has been subsiding since the mid-to-late-Eocene period. Euler deconvolution in three dimensions has been previously applied to magnetic data on the Chicxulub crater [34].
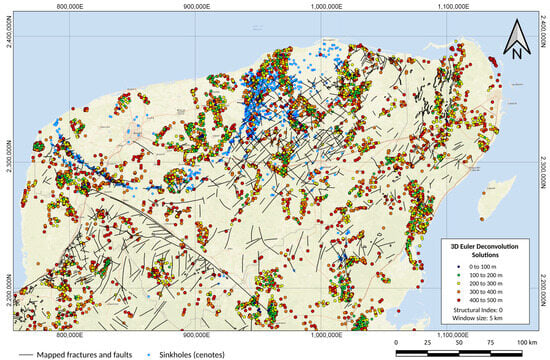
Figure 12.
Structural map derived from the application of Euler deconvolution on the Bouguer gravity map of the Yucatan Peninsula. Major sinkholes (locally known as cenotes) are included as blue circles. Black lines represent main faults mapped on the ground surface. Euler solutions associated to causative bodies (SI = 0) are plotted in colored circles ranging from 0 to 500 m.
In Figure 13, we present a regional structural map of the Yucatán Peninsula, incorporating Euler solutions ranging from 2.5 to 12.5 km in depth. This map highlights key geological features, including the ring of cenotes represented by dark blue circles, as well as primary fault patterns indicated by black lines on the surface and deeper sources denoted by blue, green, yellow, and red circles.
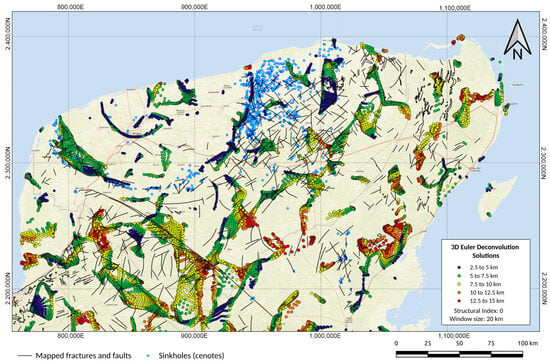
Figure 13.
Structural map derived from the application of Euler deconvolution on the Bouguer gravity map of the Yucatán Peninsula. Major sinkholes (locally known as cenotes) are included as blue circles. Black lines represent main faults mapped on the ground surface. Euler solutions associated to causative bodies (SI = 0) are plotted in colored circles ranging from 2.5 to 15 km.
The integration of deeper causative sources, estimated from Euler deconvolution within the range of 2.5 to 15 km, enhances our understanding of the structural framework of the Yucatán Peninsula. The map reveals significant regional faulting patterns spanning the entire area, with distinct rings associated with the Chicxulub impact crater clearly delineated as causative sources in dark blue circles, occurring at depths ranging from 2.5 to 5 km. Additionally, slopes of pre-existing sedimentary basins are delineated by Euler deconvolution solutions for sources within the 10–45 km depth range, identified by green and yellow colored circles.
4. Discussion
Regional analysis of the LBP model and Euler solutions in three dimensions revealed several zones with clearly differentiated geological characteristics. These zones include the Chicxulub impact basin, which was formed in the Paleogene period and covered by nearly 1 km of marine carbonate sediments; the Cenote ring, which is located on the outer edge of the Chicxulub basin, constituting a significant hydrogeological reservoir; so-called “Pockmarked Terrain”, which represents an extensive region in the north–central part of Yucatán and features a high density of faults, fractures, and karstic features; an ancient basin over the Ticul Fault manifesting as a NW-oriented structural feature.
The structural configuration revealed by gravity inversion and Euler solutions can be better understood when placed in the tectonic and geological evolution context of the Yucatán Peninsula. The formation of the Chicxulub impact crater on a heterogeneous target composed of pre-existing sedimentary basins and thick carbonate platforms significantly affected the regional tectonic architecture. The impact likely reactivated older fault systems and introduced new radial and concentric fracture patterns, which later served as conduits for karst development. The identified basins and faults may represent inherited structures that were accentuated by both the impact event and subsequent tectonic adjustments.
Tectonic subsidence associated with the post-impact relaxation of the crust, combined with carbonate sedimentation during the Paleogene–Neogene, contributed to the preservation of the basin morphology. The presence of evaporitic and dolomitic layers in the post-impact stratigraphy, as confirmed by core and well data from previous studies [5,10], suggests that differential compaction and diagenesis further enhanced the structural contrast. Additionally, geochemical data from cores and water samples [35,36] have documented variations in mineralogy and groundwater chemistry that correlate spatially with the structures identified in the inverted density models, supporting a genetic link between the tectonic architecture and hydrogeological behavior.
The formation of karst faults appears to be strongly controlled by these tectonic lineaments, particularly in zones of extensional stress or differential uplift. In this sense, the gravity-derived fault networks offer a first-order approximation of preferential flow paths and zones of enhanced permeability. Therefore, the integration of geophysical results with regional geological and geochemical knowledge provides a more comprehensive picture of how the Chicxulub event and ongoing tectonic processes have shaped the subsurface structure of northern Yucatán.
4.1. Implications for Groundwater Flow
The Yucatán Peninsula physiographic province consists of three subprovinces: Carso Yucateco, known for its limestone rocks abundant in sinkholes and cenotes, Carso and Lomeríos of Campeche, featuring undulating relief with karst limestones from the Paleocene and Eocene periods, and Costa Baja of Quintana Roo, bordering the Caribbean Sea, characterized by coastal lagoons, bays, and beaches with shallow, saline soils. Additionally, a portion of the Gulf Coastal Plain lies in the southwestern region, marked by floodplains with saturated, organically rich soils.
The continental shelf of the Yucatán Peninsula encompasses three large buried basins, including the one formed by the Chicxulub impact, with significant geohydrological implications [4,10,16,35,36]. Groundwater naturally flows into these basins due to hydraulic gradient disparities. The impact event induced extensive fracturing and heightened permeability in the limestone rocks, resulting in the formation of a vast groundwater reservoir within the Chicxulub’s ring of sinkholes [4,10,16,18,35,36]. Karst formations, prevalent on the surface of the Yucatán Peninsula, harbor significant groundwater reservoirs that are vulnerable to contamination. Interconnected underground conduits facilitate the long-distance flow of groundwater in various regions. The peninsula boasts Mexico’s most substantial karstic aquifer, punctuated by cenotes and notably forming the “ring of cenotes” in the northern part of the state of Yucatán. The high permeability of the rock enables rainwater to fully infiltrate the subsoil, eliminating significant surface currents.
This network of sinkholes constitutes an interconnected karst system, delineating the buried crater, as depicted in Figure 12. The porosity of the rock and permeability facilitate groundwater flow and substantial water storage, underscoring the importance of understanding these processes for sustainable water resource management [36,37]. Additionally, the formation of the cenote ring is linked to subsidence and faulting across the terrace zone and crater rim, resulting from groundwater percolation through the fracture zone and carbonate dissolution [5,38]. To complement the geological and hydrogeological context discussed above, Figure 14 presents a regional-scale synthesis of inferred groundwater flow directions across the Yucatán Peninsula [39]. This map integrates structural and lithological information to delineate preferential flow paths influenced by karst development and subsurface faulting patterns, highlighting the regional connectivity of the aquifer system.
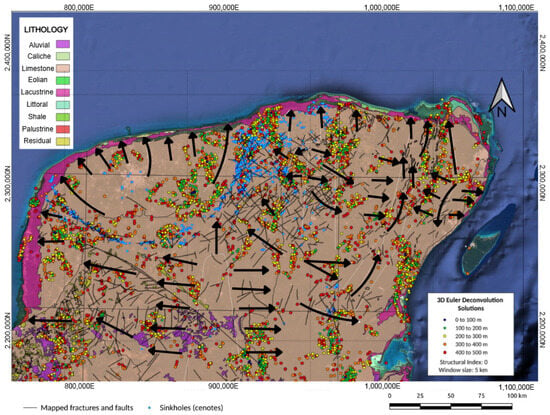
Figure 14.
Integrated geological map of the northern Yucatán Peninsula showing lithological units, mapped fractures, cenotes, and 3D Euler deconvolution solutions. The black arrows indicate interpreted fault directions and inferred preferential flow paths for groundwater. The spatial correspondence between Euler solutions, major fault alignments, and cenote distribution provides further evidence for a structurally controlled karst network along the Yucatán Peninsula.
4.2. Implications on Chicxulub Crater Morphology
The Chicxulub impact struck a massive carbonate rock layer [4,7,10,17,19,20,21,33] and an ancient valley, as illustrated in Figure 10. This ancient basin, extending beyond the 180 km diameter circular gravity anomaly, was significantly altered by the powerful impact wave. The basin’s structure now exhibits noticeable shortening and ripple patterns, with at least three distinct ripples discernible. These ripples led [17] to conclude that the Chicxulub crater spans 300 km in diameter, forming a multi-ringed basin.
However, these unique basin features are absent elsewhere on the Platform, suggesting that the asteroid impact on a heterogeneous target, comprising a compact carbonate platform and a sedimentary basin, left a distinctive mark on Earth’s surface. The diameter of a crater resulting from a meteorite impact can vary greatly due to factors such as impact speed, angle, mass, composition of the meteorite, and the nature of the impacted surface [32,40].
The formation dynamics of the Chicxulub crater were influenced by various factors, including the pre-existing geological structure of the Yucatan Peninsula, impact speed and angle, meteorite composition and energy, and other variables [41]. Consequently, the shape and formation of the crater were skewed by the specific target conditions, as previously suggested by some authors [41,42] for the case of the marine portion of the structure. When the meteorite partially struck a pre-existing sedimentary basin, the softer and less consolidated layers absorbed more impact energy, resulting in a rippled and enlarged shape in that region compared to the impact on the harder, competent limestone rocks in the surrounding platform. The ancient sedimentary basin, composed of looser materials, was more susceptible to deformation and excavation during the impact due to its deformable nature.
4.3. Geological Significance, Applications, Limitations, and Future Directions
The geological significance of the present study lies in its contribution to a better understanding of the buried structural framework of the northern Yucatán Peninsula, an area where surface geology provides limited information due to extensive carbonate cover and karst development. The identification of major sedimentary basins, fault systems, and impact-related structures provides key insights into the tectonic evolution of the region, the influence of the Chicxulub impact event, and the processes that have shaped the present-day karstic landscape. In terms of applications, the delineation of fault networks and basins has direct implications for groundwater resource management. Faults and fractures act as primary conduits for groundwater flow, and their mapping is essential for sustainable aquifer exploitation, recharge zone identification, and vulnerability assessments, particularly in karstic environments. Furthermore, the spatial correlation between gravityinferred structures and zones of intense sinkhole development suggests that these data can be used to support hazard mitigation strategies, helping to identify areas prone to subsidence, collapse, or contamination risks. Despite these contributions, several limitations must be acknowledged. The gravity inversion method (LBP) provides a regional-scale view with limited spatial resolution compared to seismic imaging. The nonuniqueness of potential field solutions, uncertainties in density contrasts, and assumptions made in the inversion and deconvolution processes introduce ambiguities that must be considered when interpreting the results. In addition, the integration of complementary datasets, such as borehole logs, hydrogeological measurements, and geochemical profiles, would further refine the interpretations. Future research directions include conducting higher-resolution geophysical surveys (e.g., seismic, resistivity, and electromagnetics) in key areas identified by this study, incorporating hydrogeological modeling constrained by geophysical data, and developing 3D hydrogeological models to predict groundwater flow paths and the extent of saltwater intrusion. Investigating the dynamic response of the karst system to climate variability and human activities also represents an important avenue for future studies aimed at ensuring the sustainability of groundwater resources in the Yucatán Peninsula.
5. Conclusions
The Yucatán Peninsula is known for its karstic carbonate terrain, lack of surface water bodies, shallow water levels, and the presence of the peninsular aquifer. In the northwest, the cenotes show a dense semicircular pattern along a topographic depression and fracture zone.
To characterize the structure and stratigraphy of the cenote ring spanning the terrace zone and the crater rim, we analyzed data from LBP gravity inversion and Euler deconvolution. These models unveiled three large buried basins, including the Chicxulub impact crater, along with its interconnected cenote ring through a karst network. Furthermore, Euler deconvolution highlights evidence of downfaulted blocks in the terrace zone along a radial fault system.
Throughout the Yucatan Platform, gravitational lows consistently mark sinkholes, cavities, and interconnected cave networks, overlaying anomalies associated with fractures and faults of various sizes.
In the eastern part of the peninsula, aquifers feature caves, sinkholes, and other geological formations resulting from extensive limestone dissolution near coastal areas. Recharge zones are widespread, as water permeates readily through cracks and fractures into the underground system.
The Yucatán Peninsula aquifer is mostly located within the homonymous physiographic province, with a small portion to the southwest in the state of Campeche within the Gulf Coastal Plain province.
In the karstic terrains of the Yucatán Platform, groundwater flow is primarily controlled by intricate networks of tunnels and fractures within limestone rocks, characterized by high secondary porosity and permeability. Existing regional geophysical datasets are insufficient for constructing geological models to simulate groundwater flow accurately. However, three-dimensional regional gravity modeling provides a glimpse into the gross structure of the upper crust up to 12.8 km thick. Further detailed geophysical surveys, combined with local hydrogeological constraints, are needed to understand flow direction patterns and the extent of saltwater intrusion near coastal zones. The main advantages of the proposed methodology are its computational efficiency, suitability for handling large regional datasets, and ability to provide a rapid first-order approximation of the shallow crustal structure. In particular, the linear back-projection (LBP) inversion offers a straightforward and low-cost alternative for imaging density variations, while the Euler deconvolution enables the identification of fault systems with minimal a priori geological information. However, some limitations should be acknowledged. The LBP method, by its nature, may produce blurred or smoothed density distributions, lacking the sharp resolution of more sophisticated inversion techniques. Moreover, Euler deconvolution results are sensitive to the choice of structural index and noise levels in the data. Future studies could benefit from integrating additional geophysical constraints or applying joint inversion strategies to refine the characterization of subsurface structures.
Author Contributions
All authors contributed to the study conceptualization and design. Material preparation, data collection, and analysis were performed by J.C.O.-A., M.N.-F., J.H.U.-F., S.O.-A., M.G.O.-d.-C., and S.L.-J. The first draft of the manuscript was written by J.C.O.-A. and all authors commented on the manuscript to update it. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the research project CONACyT-SENER number292637.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data used in this study were obtained from institutions, governmental agencies, and private companies that impose restrictions on their use and distribution. Therefore, access to the dataset is limited in accordance with the confidentiality agreements established by these entities.
Acknowledgments
The authors acknowledge the research project SENER-CONACYT 292637. Sebastian López acknowledges scholarship grant No. 2070474 from SECIHTI.
Conflicts of Interest
On behalf of all authors, the corresponding author states that there are no competing interests. The funder had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Beddows, P.A.; Smart, P.L.; Whitaker, F.F.; Smith, S.L. Decoupled fresh–saline groundwater circulation of a coastal carbonate aquifer: Spatial patterns of temperature and specific electrical conductivity. J. Hydrol. 2007, 346, 18–32. [Google Scholar] [CrossRef]
- Ramos, E.L. Geological summary of the Yucatan Peninsula. In The Gulf of Mexico and the Caribbean; Springer: Boston, MA, USA, 1975; pp. 257–282. [Google Scholar] [CrossRef]
- Weidie, A.E. Part I: Geology of Yucatan Platform; New Orleans Geological Society Special Publication; KIP Articles; New Orleans Geological Society: Mandeville, LA, USA, 1985; Volume 23, pp. 1–19. [Google Scholar]
- Perry, E.; Marin, L.; McClain, J.; Velazquez, G. Ring of cenotes (sinkholes), northwest Yucatan, Mexico: Its hydrogeologic characteristics and possible association with the Chicxulub impact crater. Geology 1995, 23, 17–20. [Google Scholar] [CrossRef]
- Monroy-Ríos, E. Advancements in our Understanding of the Yucatán Platform: Sedimentary Geology and Geochemistry, Speleogenesis, Chicxulub Ring of Cenotes, and Tectonic Stability. Ph.D. Thesis, Northwestern University, Evanston, IL, USA, 2020. [Google Scholar] [CrossRef]
- Chen, Z.; Auler, A.; Bakalowicz, M.; Drew, D.; Griger, F.; Hartmann, J.; Jiang, G.; Moosdorf, N.; Richts, A.; Stevanovic, Z.; et al. The World Karst Aquifer Mapping Project—Concept, Mapping Procedure and Map of Europe. Hydrogeol. J. 2017, 25, 771–785. [Google Scholar] [CrossRef]
- Hildebrand, A.R.; Penfield, G.T.; Kring, D.A.; Pilkington, M.; Camargo Z, A.; Jacobsen, S.B.; Boynton, W.V. Chicxulub crater: A possible Cretaceous/Tertiary boundary impact crater on the Yucatán Peninsula, Mexico. Geology 1991, 19, 867–871. [Google Scholar] [CrossRef]
- Klokočník, J.; Cílek, V.; Kostelecký, J.; Bezděk, A. Popigai and Chicxulub craters: Multiple impacts and their associated grabens. Solid Earth 2025, 16, 119–133. [Google Scholar] [CrossRef]
- Ward, W.C.; Weidie, A.E.; Back, W. Geology and Hydrogeology of the Yucatan and Quaternary Geology of Northeastern Yucatan Peninsula; New Orleans Geological Society: Mandeville, LA, USA, 1985; pp. 1–160. Available online: https://books.google.com.mx/books?id=ypdOAQAAIAAJ (accessed on 16 April 2025).
- Pope, K.O.; Ocampo, A.C.; Duller, C.E. Surficial geology of the Chicxulub impact crater, Yucatan, Mexico. Earth Moon Planets 1993, 63, 93–104. [Google Scholar] [CrossRef] [PubMed]
- Hubp, J.L.; Quesado, J.F.A.; Pereño, R.E. Rasgos geomorfológicos mayores de la Península de Yucatán. Rev. Mex. Cienc. Geol. 1992, 10, 143–150. [Google Scholar]
- Snedden, J.W.; Lowery, C.M.; Lawton, T.F. The end of the Cretaceous: Depositional palaeogeographical reconstruction of the Gulf of Mexico and adjacent areas just prior to the Chicxulub impact. Geol. Soc. Spec. Publ. 2025, 545, 739–769. [Google Scholar] [CrossRef]
- Scotese, C.R.; Vérard, C.; Burgener, L.; Elling, R.P.; Kocsis, A.T. The Cretaceous world: Plate tectonics, palaeogeography and palaeoclimate. Geol. Soc. Spec. Publ. 2025, 544, 31–202. [Google Scholar] [CrossRef]
- Ezersky, M.; Eppelbaum, L.V.; Legchenko, A. Applied Geophysics for Karst and Sinkhole Investigations: The Dead Sea and Other Regions; IOP Publishing: Bristol, UK, 2023; pp. 1–639. [Google Scholar]
- Emery, K.O. Structure and Stratigraphy of Divergent Continental Margins. In AAPG Special Volumes; American Association of Petroleum Geologists: Tulsa, OK, USA, 1977; Volume 5, pp. 1–100. [Google Scholar] [CrossRef]
- Connors, M.; Hildebrand, A.R.; Pilkington, M.; Ortiz-Aleman, C.; Chavez, R.E.; Urrutia-Fucugauchi, J.; Graniel-Castro, E.; Camara-Zi, A.; Vasquez, J.; Halpenny, J.F. Yucatán karst features and the size of Chicxulub crater. Geophys. J. Int. 1996, 127, F11–F14. [Google Scholar] [CrossRef]
- Sharpton, V.L.; Burke, K.; Camargo-Zanoguera, A.; Hall, S.A.; Lee, D.S.; Marin, L.E.; Suárez-Reynoso, G.; Quezada-Muñeton, J.M.; Spudis, P.D.; Urrutia-Fucugauchi, J. Chicxulub multiring impact basin: Size and other characteristics derived from gravity analysis. Science 1993, 261, 1564–1567. [Google Scholar] [CrossRef] [PubMed]
- Urrutia-Fucugauchi, J.; Marin, L.; Trejo-Garcia, A. UNAM scientific drilling program of Chicxulub impact structure—Evidence for a 300 kilometer crater diameter. Geophys. Res. Lett. 1996, 23, 1565–1568. [Google Scholar] [CrossRef]
- Morgan, J.; Warner, M.; Group, C.W.; Brittan, J.; Buffler, R.; Camargo, A.; Christeson, G.; Denton, P.; Hildebrand, A.; Hobbs, R.; et al. Size and morphology of the Chicxulub impact crater. Nature 1997, 390, 472–476. [Google Scholar] [CrossRef]
- Schulte, P.; Alegret, L.; Arenillas, I.; Arz, J.A.; Barton, P.J.; Bown, P.R.; Bralower, T.J.; Christeson, G.L.; Claeys, P.; Cockell, C.S.; et al. The Chicxulub asteroid impact and mass extinction at the Cretaceous–Paleogene boundary. Science 2010, 327, 1214–1218. [Google Scholar] [CrossRef]
- Gulick, S.P.S.; Christeson, G.L.; Barton, P.J.; Grieve, R.A.F.; Morgan, J.V.; Urrutia-Fucugauchi, J. Geophysical characterization of the Chicxulub impact crater. Rev. Geophys. 2013, 51, 31–52. [Google Scholar] [CrossRef]
- Adepelumi, A.A.; Flexor, J.M.; Fontes, S.L. An appraisal of the Serra da Cangalha impact structure using the Euler deconvolution method. Meteorit. Planet. Sci. 2005, 40, 1149–1157. [Google Scholar] [CrossRef]
- Batista-Rodríguez, J.A.; Pérez-Flores, M.A.; Urrutia-Fucugauchi, J. Three-dimensional gravity modeling of Chicxulub Crater structure, constrained with marine seismic data and land boreholes. Earth Planets Space 2013, 65, 973–983. [Google Scholar] [CrossRef]
- Ravat, D.; Hinze, W.J.; Hood, P.J.; Pierce, J.W.; Roest, W.R. Gradients in the interpretation of satellite-altitude magnetic data: An example from central Africa. J. Geodyn. 2002, 33, 131–142. [Google Scholar] [CrossRef]
- Reid, A.B.; Allsop, J.M.; Granser, H.; Millett, A.J.T.; Somerton, I.W. Magnetic interpretation in three dimensions using Euler deconvolution. Geophysics 1990, 55, 80–91. [Google Scholar] [CrossRef]
- Reid, A.B.; Ebbing, J.; Webb, S.J. Comment on ‘A crustal thickness map of Africa derived from a global gravity field model using Euler deconvolution’ by Getachew E. Tedla, M. van der Meijde, A. A. Nyblade and F. D. van der Meer. Geophys. J. Int. 2012, 189, 1217–1222. [Google Scholar] [CrossRef]
- Silva, J.B.C.; Barbosa, V.C.F. 3D Euler deconvolution: Theoretical basis for automatically selecting good solutions. Geophysics 2003, 68, 1962–1968. [Google Scholar] [CrossRef]
- Mikhailov, V.; Pajot, G.; Diament, M.; Price, A. Tensor deconvolution: A method to locate equivalent sources from full tensor gravity data. Geophysics 2007, 72, I61–I69. [Google Scholar] [CrossRef]
- Thompson, D.T. EULDPH: A new technique for making computer-assisted depth estimates from magnetic data. Geophysics 1982, 47, 31–37. [Google Scholar] [CrossRef]
- Pilkington, M.; Hildebrand, A.R.; Ortiz-Aleman, C. Gravity and magnetic field modeling and structure of the Chicxulub crater, Mexico. J. Geophys. Res. Planets 1994, 99, 13147–13162. [Google Scholar] [CrossRef]
- Hildebrand, A.R.; Pilkington, M.; Ortiz-Aleman, C.; Chavez, R.E.; Urrutia-Fucugauchi, J.; Connors, M.; Graniel-Castro, E.; Camara-Zi, A.; Halpenny, J.F.; Niehaus, D. Mapping Chicxulub crater structure with gravity and seismic reflection data. Geol. Soc. Lond. Spec. Publ. 1998, 140, 155–176. [Google Scholar] [CrossRef]
- Vermeesch, P.M.; Morgan, J.V. Chicxulub central crater structure: Initial results from physical property measurements and combined velocity and gravity modeling. Meteorit. Planet. Sci. 2004, 39, 1019–1034. [Google Scholar] [CrossRef]
- Ortiz-Aleman, C.; Martin, R.; Urrutia-Fucugauchi, J.; Orozco del Castillo, M.; Nava-Flores, M. Imaging the Chicxulub central crater zone from large-scale seismic acoustic wave propagation and gravity modeling. Pure Appl. Geophys. 2021, 178, 55–77. [Google Scholar] [CrossRef]
- Ortiz-Alemán, C.; Urrutia-Fucugauchi, J. Aeromagnetic anomaly modeling of central zone structure and magnetic sources in the Chicxulub crater. Phys. Earth Planet. Inter. 2010, 179, 127–138. [Google Scholar] [CrossRef]
- Kring, D.A.; Tikoo, S.M.; Schmieder, M.; Riller, U.; Rebolledo-Vieyra, M.; Simpson, S.L.; Osinski, G.R.; Gattacceca, J.; Wittmann, A.; Verhagen, C.M.; et al. Probing the hydrothermal system of the Chicxulub impact crater. Sci. Adv. 2020, 6, eaaz3053. [Google Scholar] [CrossRef]
- Pérez-Ceballos, R.; Canul-Macario, C.; Pacheco-Castro, R.; Pacheco-Ávila, J.; Euán-Ávila, J.; Merino-Ibarra, M. Regional hydrogeochemical evolution of groundwater in the ring of cenotes, Yucatán (Mexico): An Inverse Modelling Approach. Water 2021, 13, 614. [Google Scholar] [CrossRef]
- Montes-Ávila, I.; Góngora-Echeverría, V.R.; Giácoman-Vallejos, G.; Ponce-Caballero, C. Space-temporal analysis of groundwater quality in three areas of the state of Yucatán, México, and its relationship with existing anthropogenic activity. Environ. Sci. Pollut. Res. 2024, 31, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Riller, U.; Eisermann, J.O.; Kanzler, L. Causes for the formation of cenotes (sinkholes) in post-impact strata of the Chicxulub crater, Yucatán Peninsula, Mexico. In Proceedings of the EGU General Assembly 2024, Vienna, Austria, 14–19 April 2024. EGU24-3188. [Google Scholar] [CrossRef]
- Bauer-Gottwein, P.; Gondwe, B.R.N.; Charvet, G.; Marín, L.E.; Rebolledo-Vieyra, M.; Merediz-Alonso, G. Review: The Yucatán Peninsula karst aquifer, Mexico. Hydrogeol. J. 2011, 19, 507–524. [Google Scholar] [CrossRef]
- Collins, G.S.; Patel, N.; Davison, T.M.; Rae, A.S.P.; Morgan, J.V.; Gulick, S.P.S.; IODP-ICDP Expedition 364 Science Party; Third-Party Scientists. A steeplyinclined trajectory for the Chicxulub impact. Nat. Commun. 2020, 11, 1480. [Google Scholar] [CrossRef] [PubMed]
- Gulick, S.P.S.; Barton, P.J.; Christeson, G.L.; Morgan, J.V.; McDonald, M.; Mendoza-Cervantes, K.; Pearson, Z.F.; Surendra, A.; Urrutia-Fucugauchi, J.; Vermeesch, P.M.; et al. Importance of pre-impact crustal structure for the asymmetry of the Chicxulub impact crater. Nat. Geosci. 2008, 1, 131–135. [Google Scholar] [CrossRef]
- Guzmán-Hidalgo, E.; Grajales-Nishimura, J.M.; Eberli, G.P.; Aguayo-Camargo, J.E.; Urrutia-Fucugauchi, J.; Pérez-Cruz, L. Seismic stratigraphic evidence of a pre-impact basin in the Yucatán Platform: Morphology of the Chicxulub crater and K/Pg boundary deposits. Mar. Geol. 2021, 441, 106594. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).