Abstract
Understanding how climatic variables impact the reference evapotranspiration (ETo) is essential for water resource management, especially considering potential fluctuations due to climate change. Therefore, we used the Sobol’ method to analyze the spatiotemporal variations of Penman–Monteith ETo sensitivity to the climatic variables: downward solar radiation, relative humidity, maximum and minimum air temperature, and wind speed. The Sobol’ indices variances were estimated by Monte Carlo integration, with sample limits set to the 2.5th and 97.5th percentiles of the daily data of 33 automatic weather stations located in the state of Mato Grosso, Brazil. The results of the Sobol’ analysis indicate considerable spatiotemporal variations in the sensitivity of ETo to climatic variables and their interactions. The dominant climatic variable responsible for ETo fluctuations in Mato Grosso is incident solar radiation (53% to 93% of annual total sensitivity—Stot), which has a more significant impact in humid environments (70% to 90% of Stot), as observed in the areas of the Amazon biome in the state. Air relative humidity and wind speed have higher sensitivity indices during the dry season in the Cerrado biome (savanna) areas in Mato Grosso (20% and 30% of the Stot, respectively). Our findings show that changes in solar radiation, relative humidity, and wind speed are the main driving forces that impact the reference evapotranspiration.
1. Introduction
Reference evapotranspiration (ETo) is the potential evapotranspiration of a hypothetical well-watered and actively growing grass surface of uniform height [1]. Understanding the mechanism of ETo is crucial in agricultural and hydrological studies and projects at local, regional, or global scales [2,3,4,5,6,7,8], as it plays an essential role in the hydrological cycle.
Given the importance of ETo, different methods have been developed to model it, which, based on their fundamental factors, can be divided into three categories: mass transfer, radiation, and temperature equations [9,10,11,12,13,14]. The choice of the most suitable methodology typically depends on the availability of meteorological data and the required level of precision. However, it is crucial to highlight that selecting the appropriate methodology significantly and directly impacts estimating ETo and calculating hydro-climatological parameters, as stated by [15,16,17,18,19]. For instance, in [15], considerable uncertainties were observed in aridity index analysis when employing three different PET methods, potentially resulting in incorrect climatic classifications at different locations. And [16], when calculating standardized precipitation-evapotranspiration indices using the Thornthwaite model and the Hargreaves–Samani model, found that drought events appeared more severe when ETo was computed with the Thornthwaite approach.
Furthermore, choosing the right ETo methods can introduce additional uncertainties when evaluating hydro-climatological parameters, especially when considering the potential impacts of future climate changes. In many studies of climate change impacts on hydrological and water resources, only the changes in temperature and precipitation are investigated using temperature-based ETo estimation methods [20,21,22], which could lead to inaccuracies by not considering changes in solar radiation, wind speed, and relative humidity. For example, [23], in their analysis of annual ETo changes in Spain, found that relative humidity (RH), wind speed (WS), and maximum temperature (Tmax) exerted more significant influence on ETo than solar radiation (SRD) and minimum temperature (Tmin). Conversely, in Guangdong, a humid subtropical province in South China, ETo exhibited higher sensitivity to RH and temperature (T) compared to SRD and WS, as reported by [24]. In contrast, in the eastern Himalayan region of Sikkim, India [25], and the Qinghai–Tibet Plateau [26], the most influential parameter affecting ETo estimation was Tmax, followed by SRD, while WS, Tmin, and RH demonstrated varying effects on mean ETo.
In this regard, the Penman–Monteith equation, which is the standard ETo methodology recommended by the Food and Agriculture Organization (FAO), could provide better insights into how changes in climate variables can affect the ETo once it is a physical model that combines mass transfer and radiation methods, which is jointly determined by climatic variables such as downward solar radiation (SRD), relative humidity (RH), maximum and minimum temperature (Tmax and Tmin), and wind speed (WS) [1].
Currently, there is no consensus on each of the main variables causing ETo variation, especially because the Penman–Monteith ETo is influenced by a combination of changes in its climate variables, as well as the complex non-linear relationship between ETo and these parameters’ factors [27,28]. The use of sensitivity analysis can provide insight into the domain variables responsible for the fluctuations of ETo, and can provide valuable information about the response of the ETo to different climate change scenarios. Sensitivity analysis evaluates the relationships between a system’s input and output variables [29]. The methodology has been widely employed in environmental sciences, ecology, and hydrology [30]. In studies related to evapotranspiration, sensitivity analysis enables the inspection of the impact of climate variables on ETo fluctuation and the identification of its dominant variables [31,32,33].
The sensitivity analysis methodologies are commonly divided into local sensitivity analysis (LSA) and global sensitivity analysis (GSA). Although local sensitivity analysis has been widely used to identify the influence of climatic variables on ETo [34,35,36,37,38], the LSA method has no self-verification. It only reflects the local effects of individual variables [30]. On the other hand, global sensitivity analysis has the advantage of estimating the impact of all inputs and their combined effects on output changes [39,40]. The Sobol’ method is a GSA method based on variance decomposition analysis that provides a more robust performance than nonlinear models like the FAO–Penman–Monteith ETo [40,41]. Additionally, the Sobol’ method can assess the impact of uncertainties in the variables by encompassing their entire range of values, thus providing more information to quantify the influence of meteorological variables on ETo.
Amidst the Brazilian territory, the state of Mato Grosso stands out for its vast territorial area, which encompasses three biomes: the Pantanal wetlands, savanna formations (Cerrado), and the Amazon rainforest, as well as two climate types: Aw climate (tropical savanna climate) and Cwa (tropical climate) [42]. The main economic activity in the state is agricultural production, with Mato Grosso being the largest grain producer in Brazil [43]. However, despite the high demand for water resources and the potential for expanding irrigated agriculture systems, there is still a lack of research focused on the impacts that changes in climate variables have on the fluctuation of evapotranspiration in the state of Mato Grosso [44,45].
Therefore, as it is critical to identify the dominant climatic variables that control ETo in the region to better plan the use of water resources, this study has three objectives: (i) Analyzing the spatiotemporal variations in ETo and its related climatic variables (SRD, RH, Tmax, Tmin, and WS) in the state of Mato Grosso, Brazil; (ii) Determining and discussing the sensitivity of ETo to the climatic variables; (iii) Determining the dominant climatic variable attributed to ETo variability in the region.
2. Materials and Methods
2.1. Study Area and Data
The state of Mato Grosso is located between the coordinates 06°00′ S, 19°45′ S and 50°06′ W, 62°45′ W and has a large territorial extension, with an area of 903,202,446 km2, which represents 10.61% of the territory of Brazil. Climate-wise, the state has two well-defined seasons: the wet season, from October to April, and the dry season, from May to September. The total annual precipitation ranges from 1200 to 2000 mm, with higher levels in the north and east-north regions and in areas with altitudes close to 800 m. The predominant climate is classified as Aw (tropical savanna climate) and Cwa (tropical climate) according to the Köppen classification [42].
The study used daily time series data from 2008 to 2020 of the climatic variables: downward solar radiation (SRD in MJ m−2 day−1), relative air humidity (RH in %), maximum air temperature (Tmax in °C), minimum air temperature (Tmin in °C), and mean wind speed at 2 m (WS in m s−1). These data were collected from 33 automatic weather stations (AWSs) belonging to the National Institute of Meteorology (INMET), distributed throughout Mato Grosso, Brazil (Figure 1, Supplementary Table S1). Given that the wind speed variable in the INMET AWS is obtained at 10 m, the average wind speed at 2 m was calculated using Equation (1), as proposed by [1].
where WS2—is the wind speed at 2 m (m s−1), WS10—is the wind speed at 10 m (m s−1), and H—is the height at which the wind speed was obtained (m)—10 m.
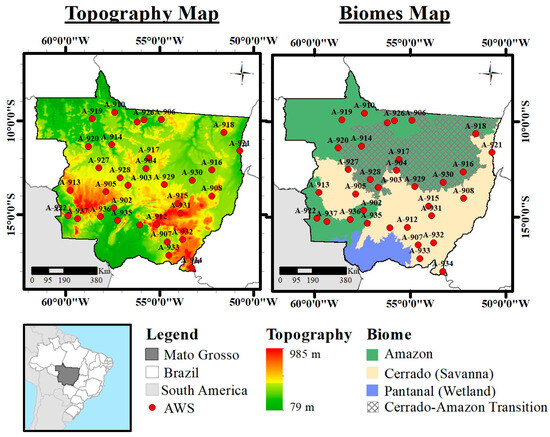
Figure 1.
Topographic and biomes maps, and location of INMET automatic weather stations (AWSs), in Mato Grosso, Brazil. Numerical identification according to Supplementary Table S1.
2.2. Data Quality Control and Homogeneity
A straightforward quality control check was conducted on the raw data by the procedures outlined by [46]. This involved removing any data that did not pass the following screening tests: (1) SRD values had to fall within the range of 3% to 100% of the radiation at the top of the atmosphere (Ra) (0.03 Ra ≤ SRD ≤ 1 Ra); (2) RH values had to range from 0% to 100% (0 ≤ RH ≤ 100); (3) Tmax had to be greater than Tmin, with both temperatures falling within the range of −30 °C to 50 °C (−30 ≤ Tmin ≤ Tmax ≤ 50); and (4) WS values had to be within the range of 0 m s−1 to 100 m s−1 (0 ≤ WS ≤ 100).
Additionally, a visual homogeneity check was conducted. This visual test involved plotting the time series data from the candidate station alongside the average data from several neighboring stations. We ensured we had a minimum of five surrounding datasets to calculate the average. No noticeable inhomogeneity was observed in the dataset, so no data was excluded.
After applying all the data treatment procedures, it was noted that there was an average of 18.6% missing values across all the datasets. Specifically, there were average missing values of 22.7% in the SRD variable, 16.4% in RH, 13.6% in Tmax, 17.9% in Tmin, and 22.5% in WS. To address these missing data points, we employed the simple linear gap-filling method provided by GapMET software, following the recommendation by [47] for AWSs in the Mato Grosso region.
2.3. Reference Evapotranspiration (ETo) Calculation
The FAO Penman–Monteith (FAO-PM) is a standardized method recognized by the Food and Agriculture Organization for estimating reference evapotranspiration (ETo). This method is based on physics and combines physiological and meteorological parameters (i.e., SRD, RH, Tmax, Tmin, and WS) to evaluate ETo at a hypothetical grass crop reference surface with an assumed crop height of 0.12 m, a fixed surface resistance of 70 s·m−1, and an albedo of 0.23 [1]. In this study, we employ the widely used FAO-56 Penman–Monteith method to calculate ETo [1], which is formulated as follows:
where ETo = reference evapotranspiration (mm d−1), Rn = net radiation at the crop surface (MJ·m−2·day−1), G = soil heat flux density at the soil surface (MJ·m−2·day−1), T = mean daily air temperature at 2 m height (mean value of Tmax and Tmin, °C), WS = wind speed at 2 m height (m·s−1), es = saturation vapor pressure (kPa), ea = actual vapor pressure (kPa), Δ = slope of saturation vapor pressure versus air temperature curve (kPa·°C−1), and γ = psychometric constant (kPa·°C−1). The detailed calculations of Rn, Δ, γ, and other parameters needed for computing ETo were obtained according to the procedure described in [1]. The G values were ignored for daily estimation (G = 0 MJ m−2 d−1).
2.4. Sobol’s Sensitivity Analysis Method
Sobol’s sensitivity analysis method [48] was utilized to evaluate the monthly sensitivity of ETo to the five meteorological variables (SRD, RH, Tmax, Tmin, WS). Sobol’s method was chosen based on its ability to perform variance decomposition analysis and its superior performance in sensitivity analysis of nonlinear and nonmonotonic models [40,41,49]. Moreover, this method allows for examining the individual variables, their interactions, and their impact on the model outputs [50]. The fundamental concept behind Sobol’s method is the decomposition of the output variance of the model (Var(Y)) (Equation (3)), allowing verification of the contribution that each variable (X1, X2,…, Xd) and their interaction has on the output.
where Vi is the contribution to Var(Y) due solely to the effect of Xi, and Vi,2,…,d is the contribution to Var(Y) due to the interaction of {X1, X2,…, Xd}. Subsequently, the method allows separating the contribution of each variable by estimating the Sobol’ first-order index (S1) (Equation (4)), as well as the variable interactions contribution by estimating the Sobol’ total-sensitivity index (Stot) (Equation (5)):
The detailed Sobol’ decomposition analyses can be found in [51]. This study calculated the Sobol’ decomposition and its indices using the Global Sensitivity Analysis Toolbox Version 1.57 of the program MATLAB [52]. To calculate the Sobol’ Index, we first needed to generate samples for each meteorological variable (SRD, RH, Tmax, Tmin, WS). This involved initially dividing the datasets of each variable from the AWSs into 12 subsets, each representing a month. From these subsets, we extracted the variables’ probability density function (PDF), along with their maximum and minimum ranges. The variable ranges were determined as the 2.5th and 97.5th percentiles of the daily observed data for each month and AWS (see Supplementary Tables S5 and S6). Subsequently, we used Monte Carlo quasi-random numerical integration to create 20,000 samples for each variable per month per AWS. These samples were then utilized to estimate ETo, and the Global Sensitivity Analysis Toolbox was applied to compute the Sobol’ Indices based on the variance of the estimated ETo.
Given that Tmin cannot exceed Tmax, we followed the approach recommended by [39,53] when generating samples for these variables using the Monte Carlo method. Initially, we calculated the mean and the difference between Tmax and Tmin. Subsequently, we generated samples for mean temperature and temperature differences using the Monte Carlo technique. Finally, we reconstructed the minimum and maximum temperatures from the generated samples.
2.5. Spatial Interpolation
The ESRI ArcGIS® 10.8 (Environmental Systems Research Institute, Redlands, CA, USA), ordinary kriging model was used to create interpolation maps for ETo and its variables and sensitivity results across the entire study area. The ArcGIS Geostatistical Analyst tools were employed to generate a nested variogram with multiple model fits automatically. Additionally, a cross-validation method was executed to compare predicted and observed values, enabling the assessment of the model’s performance and fine-tuning of variogram parameters.
3. Results
3.1. Climatic Variables and Penman–Monteith ETo Spatiotemporal Distribution
The monthly mean of solar radiation (SRD), relative humidity (RH), maximum and minimum air temperature (Tmax, Tmin), wind speed (WS), and reference evapotranspiration (ETo) at the 33 AWS in Mato Grosso, Brazil are represented by the boxplots in Figure 2. All variables follow a seasonal pattern between wet and dry seasons. Tmax and WS reach their highest mean at the end of the dry season (38.4 ± 1.3 °C and 1.3 ± 0.5 m s−1), whereas their lowest mean happens at the end of the wet season (33.8 ± 1.3 °C and 0.9 ± 0.3 m s−1). Tmin and RH means range from 14.6 ± 1.0 °C to 20.0 ± 1.0 °C, and 52.6 ± 7.1% to 83.0 ± 2.5%, with a maximum in the wet season and minimum in the dry season. The lowest mean SRD is during the beginning of the dry season (16.2 ± 2.2 MJ m−2 d−1) and gradually increases until the end of the dry season when it reaches its highest mean (19.1 ± 1.4 MJ m−2 d−1). The beginning of the dry season also exhibits the lowest ETo (3.5 ± 0.3 mm d−1). The evapotranspiration demand increases during the dry period, reaching its maximum in September (5.0 ± 0.6 mm d−1) and remaining relatively constant during the wet season (about 4.1 ± 0.3 mm d−1).
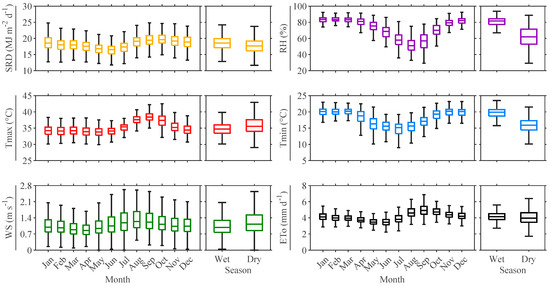
Figure 2.
Boxplot showing the monthly variation of Penman–Monteith reference evapotranspiration (ETo) and its climatic variables obtained on 33 weather stations (AWSs) of Mato Grosso, Brazil. (Data series from 2008–2020). Climatic variables: SRD—downward solar radiation; RH—relative humidity; Tmax—maximum air temperature; Tmin—minimum air temperature; WS—wind speed at 2 m. The top and bottom edges of the box represent the 75th and 25th percentiles. The top and bottom whiskers represent the nonoutlier maximum and minimum. The line inside each box is the median. The gray-shaded background represents the rainy season. Empty and full boxes also indicate monthly values in the rainy and dry seasons, respectively. The different colors represent the meteorological variables evaluated (yellow—SRD; purple—RH; red—Tmax; blue—Tmin; green—WS; black—ETo).
The spatial distribution of evapotranspiration and its climatic variables on an annual and seasonal scale is displayed in Figure 3. The results show a zonal variation that follows the distribution of biomes and topography in Mato Grosso. The Amazon region of the state exhibits the lowest values of SRD, Tmax, WS, and ETo, and the highest values of Tmin and RH. In the Cerrado region, the influence of topography can also be observed in higher-altitude areas (southeast part of the state), where there is a decrease in SRD, Tmax, Tmin, and ETo compared to the rest of the biome in the state. The spatial distribution of variables within the state is less noticeable during the wet season because there is a similar pattern in the average values of SRD, RH, and Tmin across both biomes in Mato Grosso.
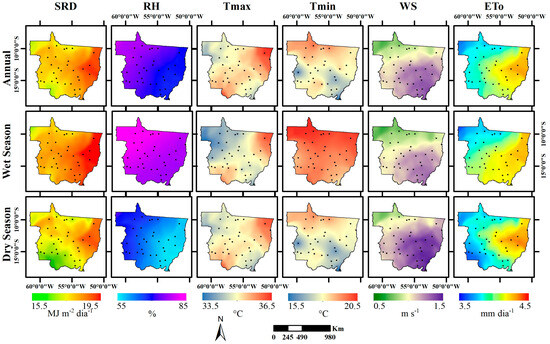
Figure 3.
Spatial distribution of Penman–Monteith reference evapotranspiration (ETo) and climatic variables in the 33 weather stations (AWSs) of Mato Grosso, Brazil. (Data series from 2008–2020). Climatic variables: SRD—downward solar radiation; RH—relative humidity; Tmax—maximum air temperature; Tmin—minimum air temperature; WS—wind speed at 2 m. Lines on the map represent the biome limits, and points represent the automatic weather stations (AWSs) of the state of Mato Grosso.
3.2. Sobol’ Sensitivity Coefficients Spatiotemporal Distribution
Figure 4 shows the variation of sensitivity indices for the meteorological variables of ETo obtained from the 33 AWSs on an annual and seasonal time scale. Figure 5 presents the monthly variation of these sensitivity indices. Based on the method proposed by [51], the sensitivity indices of the first order (S1) and total (Stot) can be classified into three levels of sensitivity: insensitive (S < 0.01), sensitive (S ≥ 0.01), and highly sensitive (S ≥ 0.1). Thus, among the five meteorological variables, ETo is highly sensitive to SRD, RH, and WS sensitive to Tmax; and insensitive to Tmin.
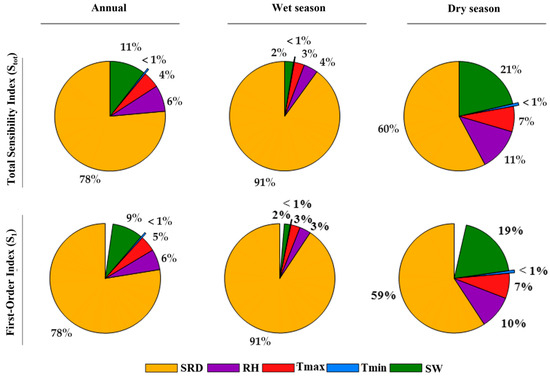
Figure 4.
Annual and seasonal of Sobol’s first-order and total sensitivity indices of the climatic variables used to estimate Penman–Monteith reference evapotranspiration (ETo) in Mato Grosso, Brazil. Climatic variables: SRD—downward solar radiation; RH—relative humidity; Tmax—maximum air temperature; Tmin—minimum air temperature; WS—wind speed at 2 m.
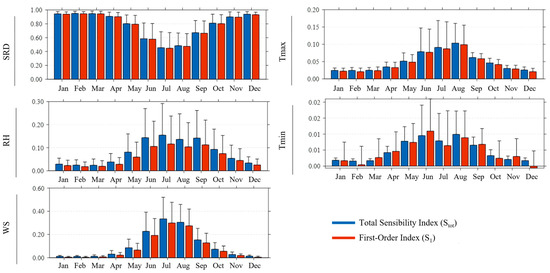
Figure 5.
Monthly variations of Sobol’s first-order and total sensitivity indices of the climatic variables used to estimate Penman–Monteith reference evapotranspiration (ETo) in Mato Grosso, Brazil. Climatic variables: SRD—downward solar radiation; RH—relative humidity; Tmax—maximum air temperature; Tmin—minimum air temperature; WS—wind speed at 2 m. The error bar represents the standard deviation of the indices across the 33 weather stations (AWSs) in the state of Mato Grosso, Brazil.
On the annual scale, the sensitivity indices of ETo for each variable generally followed the following order: SRD > WS > RH > Tmax > Tmin. Solar radiation (SRD) accounted for the largest variance, representing at least 59% of the total and first-order sensitivity indices during the dry period and reaching an average of 91% during the months of the rainy season. RH and WS explained approximately 8% and 11% of the Stot, and 6% and 9% of the S1 variation on an annual scale, respectively. RH and WS also alternated as the second most influential variable during the seasonal periods, with RH dominating during the rainy season and WS during the dry season. The temperature variables had a lesser influence on ETo in Mato Grosso. Throughout the year, the sensitivity indices of Tmax ranged from 3% to 10%, while Tmin reached a maximum value of approximately 1%.
The spatial distributions of the annual and seasonal averages of S1 and Stot are presented in Figure 6. The results indicate that, in addition to the seasonal behavior, the coefficients exhibit zonal characteristics that resemble the distribution of biomes in the state of Mato Grosso. Although SRD is the dominant variable in determining ETo in the state, the influence of radiation differs in the Amazon and Cerrado biomes. While in most of the Amazon region, the sensitivity indices of SRD are on average higher than 80%, in the Cerrado biome, the sensitivity of ETo to radiation ranges from 40% to 80%, indicating that RH, WS, and Tmax also influence ETo fluctuations in the Cerrado.
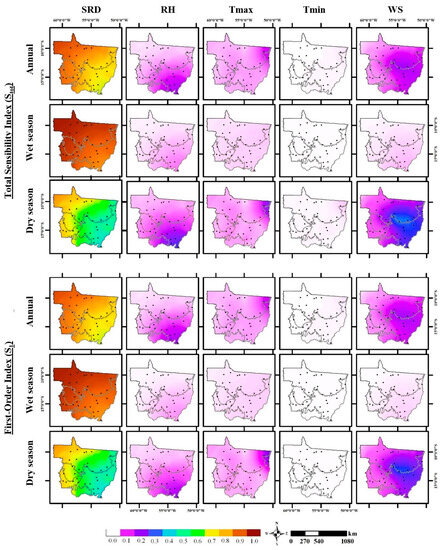
Figure 6.
Spatial distribution of Sobol’s first-order and total sensitivity indices of the climatic variables used in the estimation of Penman–Monteith reference evapotranspiration (ETo) in the state of Mato Grosso, Brazil, on an annual and seasonal scale. Climatic variables: SRD—downward solar radiation; RH—relative humidity; Tmax—maximum air temperature; Tmin—minimum air temperature; WS—wind speed at 2 m. Lines on the map represent the biome limits, and points represent the automatic weather stations (AWSs) in Mato Grosso.
During the dry season of the Cerrado biome, when the sensitivity indices of SRD are around 50%, it is possible to observe that the second dominant variable varies according to the spatial distribution. In the southeast of the Cerrado, RH becomes the second dominant variable, accounting for 20% to 30% of the ETo variation. In the northeastern region of the Cerrado, Tmax becomes the second dominant variable, with approximately 20% to 30% influence. In the central region of the Cerrado, the second dominant variable is WS, with sensitivity indices ranging from 30% to 40%.
4. Discussion
Understanding the causes of ETo variations is essential for water resources management and agriculture in Mato Grosso. The results of this study have highlighted the high sensitivity of Penman–Monteith ETo to solar radiation in the study area. Overall, the sensitivity of ETo to the five meteorological variables in the state can be ranked as follows: SRD > WS ≥ RH > Tmax > Tmin. Although SRD is the dominant climatic variable, explaining 60% to 90% of the ETo variability throughout the year, the sensitivity of ETo the climatic variables, similar to findings in the literature, showed strong indications of spatial variability (Figure 4 and Figure 6); [32,54,55], with RH playing an important role in determining the spatial and seasonal variations of ETo sensitivity indices in Mato Grosso.
In the Mato Grosso Amazon biome portion, higher and relatively constant relative humidity percentages are observed throughout the year, along with lower values and greater fluctuation of incident radiation measurements (Figure 3 and Figure 4). The main cause for this pattern is that the Amazon region is characterized as a humid tropical area where convective activity forces the upward movement of moisture, forming a thicker cloud cover than the Cerrado region of Mato Grosso [56]. Consequently, in this biome, not only is there a greater attenuation of solar radiation, but there is also a greater reduction in temperature amplitude. This combination of factors could explain why solar radiation is the limiting factor in the evapotranspiration process in the Amazon biome.
These results are consistent with those found in other humid subtropical and tropical areas, such as in the forests of China [55,57], where it is reported that changes in incident solar radiation are the main driving force for ETo variability. Similar behavior can also be observed in the Cerrado region of Mato Grosso during the wet season, when relative humidity generally exceeds 80%. During this season, maximum temperature and temperature amplitude are lower, and cloud cover increases due to the predominant circulation of the continental equatorial mass (mEc) and the South Atlantic Convergence Zone (ZCAS), which transport moisture from the Amazon to the Cerrado region (Figure 6) [56,58,59], impacting the solar radiation sensitivity indices.
During the dry season in the Cerrado biome region, the spatial distribution of sensitivity indices indicates three areas of influence analogous to the subdivision of the biome proposed by [58]: Cerrado Meridional (southeastern region of the Mato Grosso Cerrado), Cerrado Central, and Cerrado Setentrional (northeastern region of the Mato Grosso Cerrado). In the Cerrado Meridional region, the occasional incursion of air circulation masses from the polar mass (mP), combined with the topography, leads to increased cloudiness and lower average incident radiation (Figure 6) [59,60,61]. However, an increase in RH sensitivity indices is observed due to lower averages and greater fluctuations in relative humidity (RH) compared to the Amazon biome. In the Cerrado Central and Setentrional regions, the reduction in atmospheric humidity caused by the tropical Atlantic mass and the flat topography creates clearer sky conditions [56,58,59,61], thereby reducing fluctuations in incident solar radiation. In this scenario, the increase in sensitivity indices for the variables is linked to their ability to increase water retention in the atmosphere. Therefore, in the Cerrado Setentrional region, where Tmax reaches the highest values in the state, Tmax has greater sensitivity than RH and WS, as it allows for an increase in the saturation vapor pressure deficit. On the other hand, in the Cerrado Central region, where Tmax is lower and WS is higher, wind speed has a greater influence due to disturbances and movement in the atmospheric boundary layer.
These results are consistent with those found by [41,55,62,63], which indicate that atmospheric air circulation directly influences the spatial patterns of global ETo sensitivity. These authors also agree that high cloudiness and relative humidity conditions are the main factors that increase the sensitivity indices of radiation. In contrast, clear sky conditions and low relative humidity increase the sensitivity indices of wind speed. Thus, ETo is more sensitive to changes in SRD, WS, and RH variables in arid and semi-arid regions.
The temperature variables (Tmax and Tmin) generally accounted for less than 10% of ETo. Although higher temperatures, resulting in reduced RH and increased energy supply to the process, tend to increase ETo, the effects of Tmax and Tmin on ETo sensitivity, as observed in studies by [41,55,62,64], were almost insignificant compared to other factors.
The Sobol’ method has provided valuable insights for understanding the impact of climatic variables on ETo. Based on our results, caution should be exercised when making future ETo estimates in Mato Grosso State using formulations that do not account for changes in solar radiation, wind speed, and relative humidity. Please pay special attention to the estimation of Rs, as it is the dominant variable in Penman–Monteith ETo calculations. Furthermore, in the Mato Grosso Cerrado region, particularly during the dry period, the interactions between relative humidity and wind speed cannot be disregarded when determining evapotranspiration using the Penman–Monteith method.
5. Conclusions
The global sensitivity of ETo estimated by the Penman–Monteith method to meteorological variables (downward solar radiation—SRD, relative humidity—RH, maximum air temperature—Tmax, minimum air temperature—Tmin, and wind speed at 2 m—WS) exhibits seasonal and spatial distribution in Mato Grosso State.
Regardless of the period, the dominant variable for evapotranspiration in Mato Grosso is solar radiation (SRD), which has the greatest influence during the rainy season and in humid regions such as the Amazon. The other variables that have a secondary impact on sensitivity follow the ranking of WS > RH > Tmax > Tmin.
ETo estimated by the Penman–Monteith method is most sensitive to changes in WS, RH, and Tmax in arid and semi-arid environments, such as the Cerrado during the dry season. However, the sensitivity to RH and WS is higher in the Meridional and Central regions of the Cerrado biome. In contrast, in the Setentrional region, the secondary variable with the highest sensitivity is Tmax.
The meteorological variable Tmin does not significantly influence ETo estimated by the Penman–Monteith method in the Mato Grosso State.
The estimation of ETo using the Penman–Monteith method for Mato Grosso State needs more accurate and precise data on incident solar radiation (SRD), whether obtained from observed data series at meteorological stations or estimated through gap-filling methods.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/earth4030038/s1. Table S1: INMET automatic weather stations (AWSs) in Mato Grosso, Brazil. Table S2: Lower and upper sample limits (Inf—Sup), corresponding to the 2.5th and 97.5th percentiles, of the meteorological variable downward solar radiation (SRD—MJ m−2 day−1) observed in the 33 AWSs of Mato Grosso State, Brazil. Table S3: Lower and upper sample limits (Inf—Sup), corresponding to the 2.5th and 97.5th percentiles, of the meteorological variable relative humidity (RH—%) observed in the 33 AWSs of Mato Grosso State, Brazil. Table S4: Lower and upper sample limits (Inf—Sup), corresponding to the 2.5th and 97.5th percentiles, of the meteorological variable maximum air temperature (Tmax—°C) observed in the 33 AWSs of Mato Grosso State, Brazil. Table S5: Lower and upper sample limits (Inf—Sup), corresponding to the 2.5th and 97.5th percentiles, of the meteorological variable minimum air temperature (Tmin—°C) observed in the 33 AWSs of Mato Grosso State, Brazil. Table S6: Lower and upper sample limits (Inf—Sup), corresponding to the 2.5th and 97.5th percentiles, of the meteorological variable wind speed at 2 m. (WS—m s−1) observed in the 33 AWSs of Mato Grosso State, Brazil.
Author Contributions
Conceptualization, M.S. and A.P.d.S.; Methodology, M.S.; Software, M.S.; Validation, M.S.; Formal analysis, M.S.; Investigation, M.S. and A.P.d.S.; Resources, A.P.d.S.; Data curation, M.S. and A.P.d.S.; writing—original draft preparation, M.S.; writing—review and editing, M.S. and A.P.d.S.; Visualization, A.P.d.S.; Supervision, A.P.d.S.; Project administration, A.P.d.S.; funding acquisition, A.P.d.S. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financed in part by the Fundação de Amparo a Pesquisa do Estado de Mato Grosso (Process 082944/2017) and by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001. The authors wish to thank the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for their support with a productivity grant (Process 308784/2019-7).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The automatic weather stations (AWSs) data used in this study can be accessed by the Instituto Nacional de Meteorologia (INMET) databank website: https://bdmep.inmet.gov.br/# (accessed on 31 July 2023).
Acknowledgments
The authors also thank all the students and professors of the “Interações Ambiente e Planta” Research Group (http://dgp.cnpq.br/dgp/espelhogrupo/40759) (accessed on 31 July 2023).
Conflicts of Interest
The authors declare no conflict of interest. Supporting entities had no role in the study’s design; in the collection, analysis, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Liu, B.; Xu, M.; Henderson, M.; Gong, W. A spatial analysis of pan evaporation trends in China, 1955–2000. J. Geophys. Res. 2004, 109, D15102. [Google Scholar] [CrossRef]
- McVicar, T.R.; Van Niel, T.G.; LI, L.T.; Hutchinson, M.F.; Mu, X.M.; Liu, Z.H. Spatially distributing monthly reference evapotranspiration and pan evaporation considering topographic influences. J. Hydrol. 2007, 338, 196–220. [Google Scholar] [CrossRef]
- Gu, S.; Tang, Y.; Cui, X.; Du, M.; Zhao, L.; Li, Y.; Xu, S.; Zhou, H.; Kato, T.; Qi, P.; et al. Characterizing evapotranspiration over a meadow ecosystem on the Qinghai-Tibetan Plateau. J. Geophys. Res. 2008, 113, D08118. [Google Scholar] [CrossRef]
- Van der Velde, Y.; Lyon, S.W.; Destouni, G. Data-driven regionalization of river discharges and emergent land cover evapotranspiration relationships across Sweden. J. Geophys. Res. Atmos. 2013, 118, 2576–2587. [Google Scholar] [CrossRef]
- Araújo Neto, R.A.; dos Santos Nascimento, J.W.; de Oliveira, F.F.; Rebelo, G.R.P.; de Lima Silva, F.D.A.; de Carvalho, A.L. Models generated by multiple regression in filling meteorological data failures in an automatic meteorological station in Alagoas. Rev. Geama. 2020, 6, 4–10. [Google Scholar]
- Xiang, K.; Li, Y.; Horton, R.; Feng, H. Similarity and difference of potential evapotranspiration and reference crop evapotranspiration—A review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
- Sarnighausen, V.C.R.; Gomes, F.G.; Dal Pai, A.; Rodrigues, S.A. Estimativa da evapotranspiração de referência para Botucatu-SP por meio de modelos de regressão. RBCLima 2021, 28, 766–787. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. 1948, 193, 120–145. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Blaney, H.F.; Criddle, W.D. Determining water requirements in irrigated areas from climatological irrigation data. Tech. Pap. 1950, 96, 48. [Google Scholar]
- Harbeck, G.E. A Practical Field Technique for Measuring Reservoir Evaporation Utilizing Mass-Transfer Theory; USGS Professional Paper 272-E:101–105; US Geological Survey: Reston, VA, USA, 1962. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of the surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Guitjens, J.C. Models of Alfalfa Yield and Evapotranspiration. J. Irrig. Drain. Eng. 1982, 108, 212–222. [Google Scholar] [CrossRef]
- Tegos, A.; Stefanidis, S.; Cody, J.; Koutsoyiannis, D. On the Sensitivity of Standardized-Precipitation-Evapotranspiration and Aridity Indexes Using Alternative Potential Evapotranspiration Models. Hydrology 2023, 10, 64. [Google Scholar] [CrossRef]
- Ortiz-Gómez, R.; Flowers-Cano, R.S.; Medina-García, G. Sensitivity of the RDI and SPEI Drought Indices to Different Models for Estimating Evapotranspiration Potential in Semiarid Regions. Water Resour. Manag. 2022, 36, 2471–2492. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, W.; Li, Y.; Hu, M.; Cheng, L.; Wang, X. Variation in evapotranspiration due to climate change and its impact on hydrological processes in the Yellow River Basin, China. Hydrol. Process. 2022, 36, 546–556. [Google Scholar]
- Li, X.; Hao, Z.; Liu, Y.; Guo, T.; Zhang, Y.; Cheng, L. Comparison of three potential evapotranspiration models in different climate zones in China. J. Hydrol. 2021, 606, 127770. [Google Scholar]
- Liu, L.; Zhang, H.; Guo, S. Application of artificial neural network in forecasting rainfall and flood in Shenzhen. J. Phys. Conf. Ser. 2020, 1639, 012051. [Google Scholar]
- Jha, M.; Pan, Z.; Takle, E.S.; Gu, R. Impacts of climate change on streamflow in the Upper Mississippi River Basin: A regional climate model perspective. J. Geophys. Res. 2004, 109, D09105. [Google Scholar] [CrossRef]
- Wang, G.Q.; Zhang, J.Y.; Jin, J.L.; Pagano, T.C.; Calow, R.; Bao, Z.X.; Liu, C.S.; Liu, Y.L.; Yan, X.L. Assessing water resources in China using PRECIS projections and a VIC model. Hydrol. Earth Syst. Sci. 2012, 16, 231–240. [Google Scholar] [CrossRef]
- Xu, Y.P.; Pan, S.L.; Fu, G.T.; Tian, Y.; Zhang, X.J. Future potential evapotranspiration changes and contribution analysis in Zhejiang Province, East China. J. Geophys. Res.-Atmos. 2014, 119, 2174–2192. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Azorin-Molina, C.; Sanchez-Lorenzo, A.; Revuelto, J.; Morán-Tejeda, E.; López-Moreno, J.; Espejo, F. Sensitivity of Reference Evapotranspiration to Changes in Meteorological Parameters in Spain (1961–2011); John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Zhao, B.; An, D.; Yan, C.; Yan, H.; Kong, R.; Su, J. Spatiotemporal Variations of Reference Evapotranspiration and Its Climatic Driving Factors in Guangdong, a Humid Subtropical Province of South China. Agronomy 2023, 13, 1446. [Google Scholar] [CrossRef]
- Patle, G.T. Trends in major climatic parameters and sensitivity of evapotranspiration to climatic parameters in the eastern Himalayan region of Sikkim, India. J. Water Clim. Chang. 2019, 11, 491–502. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.; Yao, X.; Jiang, W. Variation in Reference Evapotranspiration over the Tibetan Plateau during 1961–2017: Spatiotemporal Variations, Future Trends and Links to Other Climatic Factors. Water 2020, 12, 3178. [Google Scholar] [CrossRef]
- Liu, T.; Li, L.; Lai, J.; Liu, C.; Zhuang, W. Reference evapotranspiration change and its sensitivity to climate variables in southwest China. Theor. Appl. Climatol. 2016, 125, 499–508. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Gang, C.; Dai, E. Attribution analyses of potential evapotranspiration changes in China since the 1960s. Theor. Appl. Climatol. 2010, 101, 19–28. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Sushan, L.; Qiongli, W. Why so many published sensitivity analyses are false: A systematic review of sensitivity analysis practices. Environ. Model Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- Irmak, S.; Payero, J.O.; Martin, D.L.; Irmak, A.; Howell, T.A. Sensitivity Analyses and Sensitivity Coefficients of Standardized Daily ASCE-Penman-Monteith Equation. J. Irrig. Drain. Eng. 2006, 6, 564–578. [Google Scholar] [CrossRef]
- Gong, L.; Xu, C.Y.; Chen, D.; Halldin, S.; Chen, Y.D. Sensitivity of the Penman-Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) basin. J. Hydrol. 2006, 329, 620–629. [Google Scholar] [CrossRef]
- Mosaedi, A.; Ghabaei, M.; Sadeghi, S.H.; Mooshakhian, Y.; Bannayon, M. Sensitivity Analysis of Monthly Reference Crop Evapotranspiration Trends in Iran: A Qualitative Approach. Theor. Appl. Climatol. 2015, 128, 857–873. [Google Scholar] [CrossRef]
- Yang, H.B.; Yang, D.W. Climatic factors influencing changing pan evaporation across China from 1961 to 2001. J. Hydrol. 2012, 414, 184–193. [Google Scholar] [CrossRef]
- Liu, Q.; Yan, C.; Ju, H.; Garré, S. Impact of climate change on potential evapotranspiration under a historical and future climate scenario in the Huang-HuaiHai Plain, China. Theor. Appl. Climatol. 2017, 132, 387–401. [Google Scholar] [CrossRef]
- Lin, P.F.; He, Z.B.; Du, J.; Chen, L.F.; Zhu, X.; Li, J. Impacts of climate change on reference evapotranspiration in the Qilian Mountains of China: Historical trends and projected changes. Int. J. Climatol. 2018, 38, 2980–2993. [Google Scholar] [CrossRef]
- Jerszurki, D.; De Souza, J.L.M.; Silva, L.D.C.R. Sensitivity of ASCE-Penman–Monteith reference evapotranspiration under different climate types in Brazil. Clim. Dyn. 2019, 53, 943–956. [Google Scholar] [CrossRef]
- Zhao, J.; Xia, H.; Yue, Q.; Wang, Z. Spatiotemporal variation in reference evapotranspiration and its contributing climatic factors in China under future scenarios. Int. J. Climatol. 2020, 40, 3813–3831. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, W.; Wang, Y.; Wang, Y.; Kang, M.; Wang, H.; Huang, Y. Sensitivity analysis of potential evapotranspiration to key climatic factors in the Shiyang River Basin. J. Water Clim. Chang. 2021, 12, 2875–2884. [Google Scholar] [CrossRef]
- Souza, A.P.; Mota, L.L.; Zamadei, T.; Martim, C.C.; Almeida, F.T.; Paulino, J. Classificação climática e balanço hídrico climatológico no estado de Mato Grosso. Nativa 2013, 1, 34–43. [Google Scholar] [CrossRef]
- Dentz, E.V. Produção agrícola no estado do Mato Grosso e a relação entre o agronegócio e as cidades: O caso de Lucas do Rio Verde e Sorriso. Atelie Geogr. 2019, 13, 165–186. [Google Scholar] [CrossRef]
- Souza, A.P.; Tanaka, A.A.; Silva, A.C.; Uliana, E.M.; Almeida, F.T.; Gomes, A.W.A.; Klar, A.E. Reference evapotranspiration by Penman-Monteith FAO 56 with missing data of global radiation. Rev. Bras. Eng. Biossistemas 2016, 10, 217–233. [Google Scholar] [CrossRef][Green Version]
- Tanaka, A.A.; Souza, A.P.; Klar, A.E.; Silva, A.C.; Gomes, A.W.A. Evapotranspiração de referência estimada por modelos simplificados para o Estado do Mato Grosso. Pesqui. Agropecu. Bras. 2016, 51, 91–104. [Google Scholar] [CrossRef]
- Xavier, A.C.; Scanlon, B.R.; King, C.W.; Alves, A.I. New improved Brazilian daily weather gridded data (1961–2020). Int. J. Climatol. 2022, 42, 8390–8404. [Google Scholar] [CrossRef]
- Sabino, M.; Souza, A.P.D. Gap-filling meteorological data series using the GapMET software in the state of Mato Grosso, Brazil. Rev. Bras. Eng. Agricola Ambient. 2022, 27, 149–156. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity Estimates for Nonlinear Mathematical Models. Math. Model. Comput. Exp. 1993, 4, 407–414. [Google Scholar]
- Yang, J. Convergence and uncertainty analyses in Monte-Carlo based sensitivity analysis. Environ. Modell. Softw. 2011, 26, 444–457. [Google Scholar] [CrossRef]
- Zhang, K.; Zhu, G.; Ma, J.; Yang, Y.; Shang, S.; Gu, C. Parameter analysis and estimates for the MODIS evapotranspiration algorithm and multiscale verification. Water Resour. Res. 2019, 55, 2211–2231. [Google Scholar] [CrossRef]
- Tang, Y.; Reed, P.; Wagener, T.; Van Werkhoven, K. Comparing sensitivity analysis methods to advance lumped watershed model identification and evaluation. Hydrol. Earth Syst. Sci. 2007, 11, 793–817. [Google Scholar] [CrossRef]
- Flax, M. Global Sensitivity Analysis Toolbox. MATLAB Central File Exchange. 2023. Available online: https://www.mathworks.com/matlabcentral/fileexchange/40759-global-sensitivity-analysis-toolbox (accessed on 3 September 2023).
- Pan, S.; Fu, G.; Chiang, Y.M.; Ran, Q.; Xu, Y. A two-step sensitivity analysis for hydrological signatures in Jinhua River Basin, East China. Hydrol. Sci. J. 2017, 62, 2511–2530. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, S.; Mo, X.; Shu, C.; Sun, Y.; Zhang, C. Assessing the impact of climate change on potential evapotranspiration in Aksu River Basin. J. Geogr. Sci. 2011, 21, 609–620. [Google Scholar] [CrossRef]
- Fan, Z.X.; Thomas, A. Decadal changes of reference crop evapotranspiration attribution: Spatial and temporal variability over China 1960–2011. J. Hydrol. 2018, 560, 461–470. [Google Scholar] [CrossRef]
- Arias, P.A.; Fu, R.; Hoyos, C.D.; Li, W.; Zhou, L. Changes in cloudiness over the Amazon rainforests during the last two decades: Diagnostic and potential causes. Clim. Dyn. 2011, 37, 1151–1164. [Google Scholar] [CrossRef][Green Version]
- Stanhill, G.; Cohen, S. Global dimming: A review of the evidence for a widespread and significant reduction in global radiation with discussion of its probable causes and possible agricultural consequences. Agr. Forest Meteorol. 2001, 107, 255–278. [Google Scholar] [CrossRef]
- Nascimento, D.T.F.; Novais, G.T. Clima do Cerrado: Dinâmica atmosférica e características, variabilidades e tipologias climáticas. Élisée 2020, 9, e922021. [Google Scholar]
- Diniz, F.D.A.; Ramos, A.M.; Rebello, E.R.G. Brazilian climate normals for 1981–2010. Pesqui. Agropecu. Bras. 2018, 53, 131–143. [Google Scholar] [CrossRef]
- Garreaud, R. Cold air incursions over subtropical and tropical South America: A numerical case study. Mon. Weather Rev. 1999, 127, 2823–2853. [Google Scholar] [CrossRef]
- Sette, D.M. Os climas do cerrado do Centro-Oeste. RBCLima 2005, 1, 29–42. [Google Scholar] [CrossRef]
- Taban, H.; Talaee, P.H. Sensitivity of evapotranspiration to climate change in different climates. Glob. Planet. Chang. 2014, 115, 16–23. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, Z.X.; Zuo, D.P.; Wang, X.M. Temporal variations of reference evapotranspiration and its sensitivity to meteorological factors in Heihe River Basin, China. Water Sci. Eng. 2015, 8, 1–8. [Google Scholar] [CrossRef][Green Version]
- Zhao, Y.F.; Zou, X.Q.; Zhang, J.X.; Cao, L.; Xu, X.; Zhang, K.; Chen, Y. Spatio-temporal variation of reference evapotranspiration and aridity index in the Loess Plateau Region of China, during 1961–2012. Quat. Int. 2014, 349, 196–206. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).