Optimal Coordinated Control of DC Microgrid Based on Hybrid PSO–GWO Algorithm †
Abstract
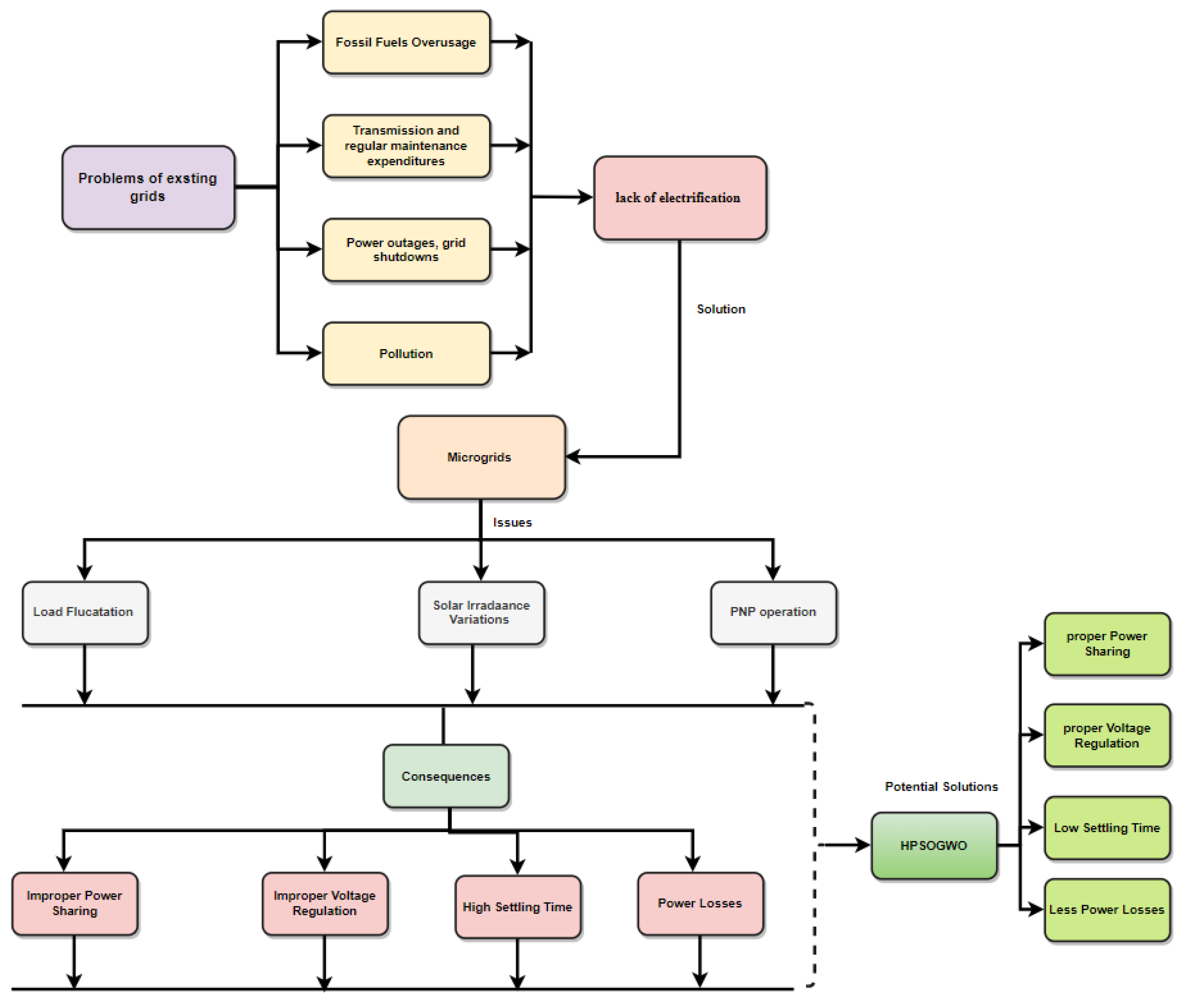
:1. Introduction
2. Modeling of the Local Control Layer in DCMG
2.1. DC MG Control
2.2. PV Side Control Strategy
2.3. Hybrid Battery/SC Side Control Strategy
3. Design Considerations of the DC–DC Power Converters
3.1. Boost Converter
3.2. Buck-Boost Converter
4. Proposed Control Method
4.1. HPSO–GWO Algorithm
4.2. Problem Formulation
- Initialize the grey wolf’s populations, X1, X2, X3, etc., which indicates that each wolf (X) represents Kp and Ki.
- Initialize parameters , and , as their capabilities for exploration and development may be leveraged to achieve a better balance in the GWO algorithm.
- Compute the fitness value of each agent (grey wolf) to determine the best three wolves.
- The placements of the best three wolves regarding targeted prey can be determined, based on Equations (11)–(17).
- The locations and velocities of the best wolves are updated, based on Equations (18) and (19), respectively.
- In case the current iteration is less than the maximum iterations limit, based on step 3, all other wolves (ω) will update the positions. Otherwise, the optimal values of X agents (Kp and Ki) will be obtained to be applied in the system.
- Based on the first condition in step 4, , and will be updated accordingly. Then, the value of each search agent (wolf) is recalculated.
- Based on the previous updates, the best position is updated. This process continues until the best values of Kp and Ki are obtained.
- Figure 4 depicts all these steps.
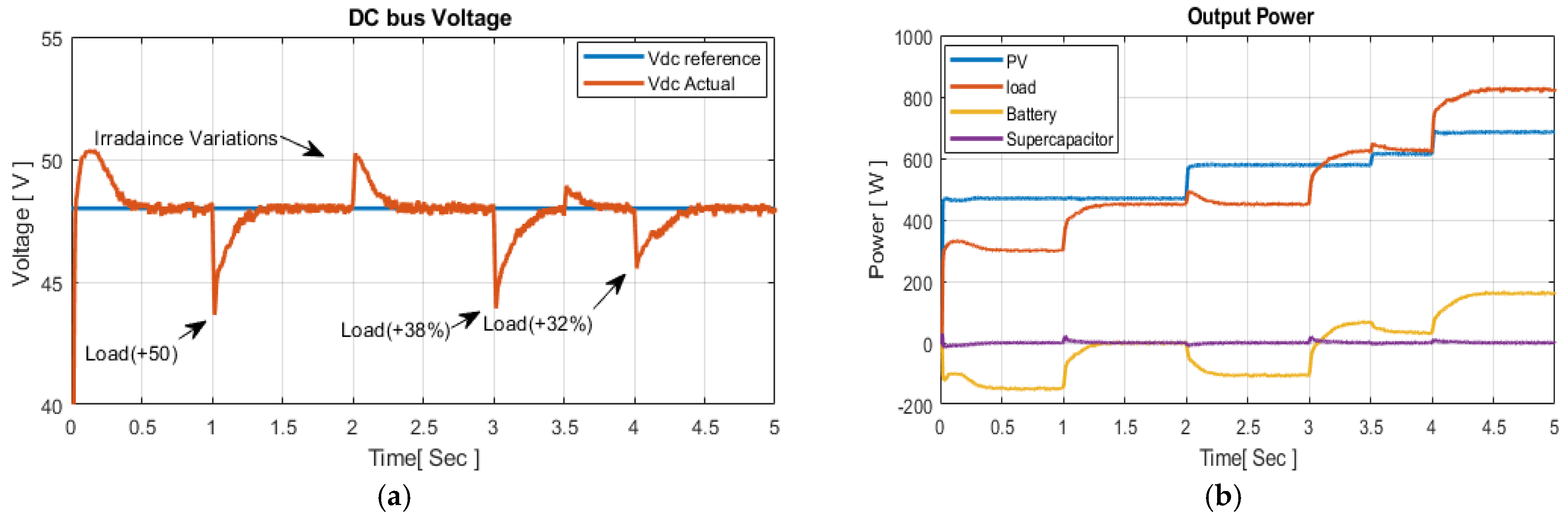
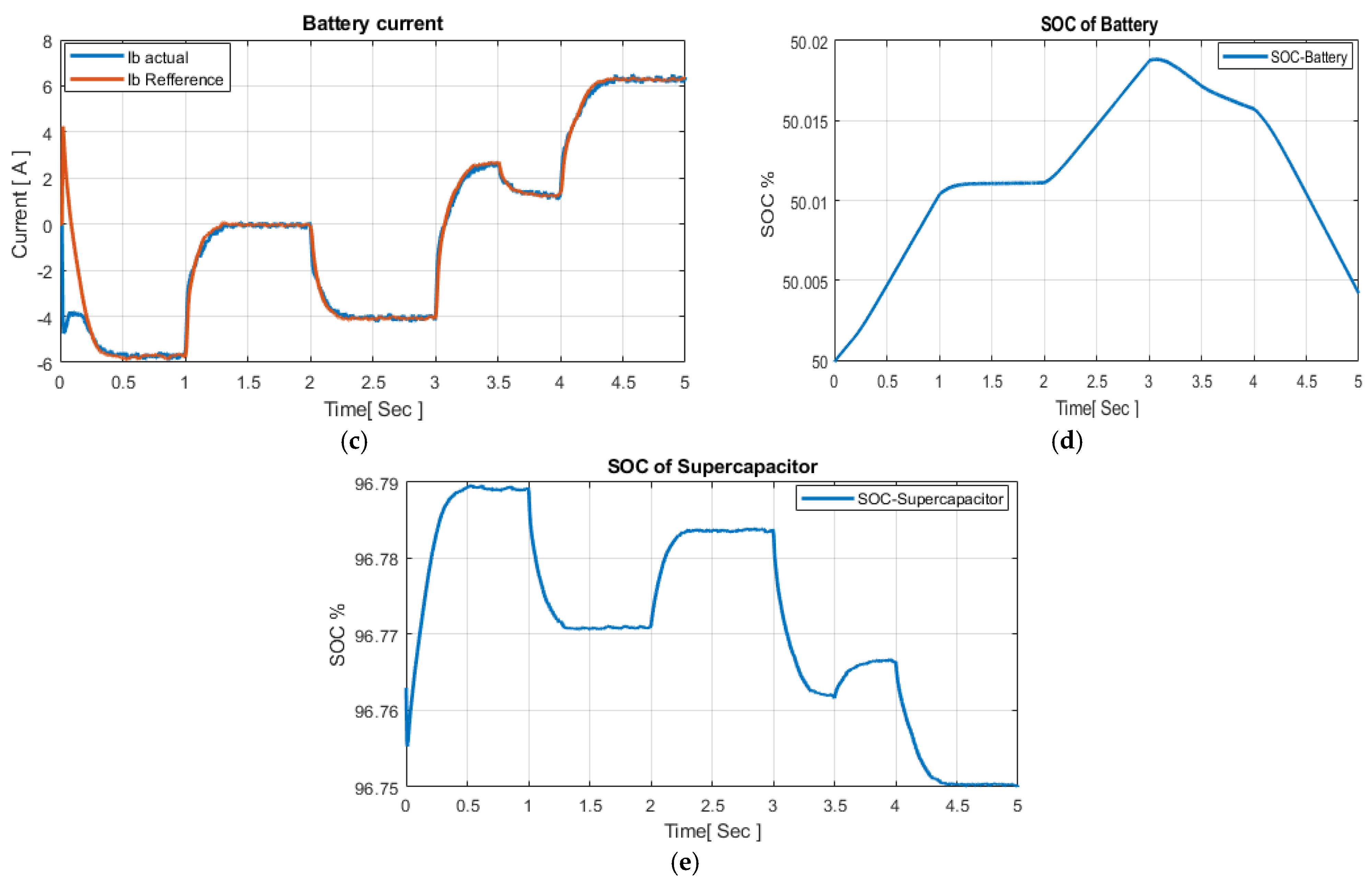
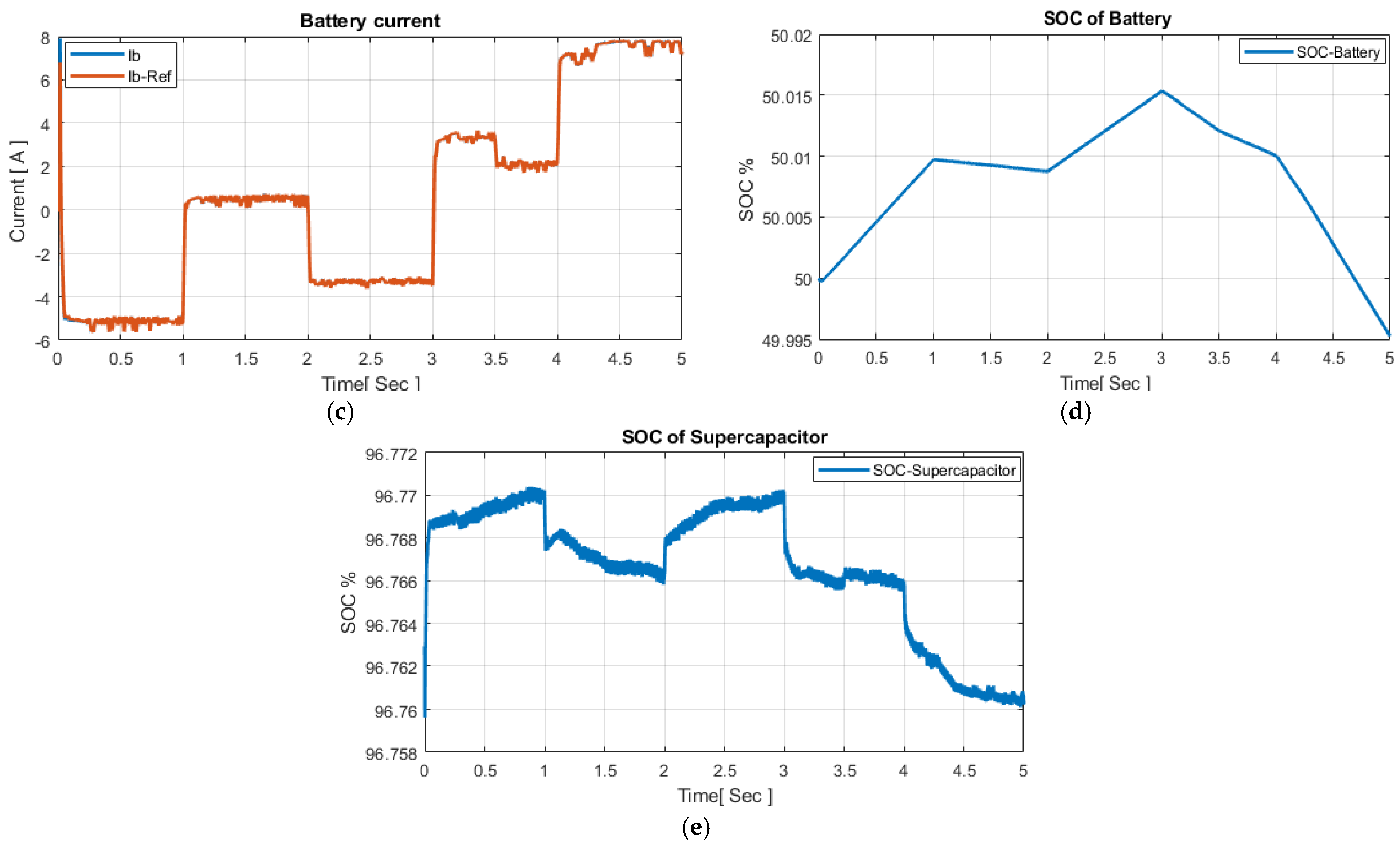
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sanjeev, P.; Padhy, N.P.; Agarwal, P. Autonomous Power Control and Management between Standalone DC Microgrids. IEEE Trans. Ind. Inform. 2018, 14, 2941–2950. [Google Scholar] [CrossRef]
- Abhishek, A.; Ranjan, A.; Devassy, S.; Verma, B.K.; Ram, S.K.; Dhakar, A.K. Review of hierarchical control strategies for DC microgrid. IET Renew. Power Gener. 2020, 14, 1631–1640. [Google Scholar] [CrossRef]
- Gholami, M.; Pisano, A. Model Predictive Operation Control of Islanded Microgrids under Nonlinear Conversion Losses of Storage Units. Electricity 2022, 3, 33–50. [Google Scholar] [CrossRef]
- Ali, S.; Shengxue, T.; Jianyu, Z.; Ali, A.; Nawaz, A. An Implementation of parallel buck converters for common load sharing in DC microgrid. Information 2019, 10, 91. [Google Scholar] [CrossRef] [Green Version]
- Rezaei, O.; Mirzapour, O.; Panahazari, M.; Gholami, H. Hybrid AC/DC Provisional Microgrid Planning Model Considering Converter Aging. Electricity 2022, 3, 236–250. [Google Scholar] [CrossRef]
- Al-Ismail, F.S. DC Microgrid Planning, Operation, and Control: A Comprehensive Review. IEEE Access 2021, 9, 36154–36172. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Sinha, A.K.; Kishore, N.K. Control Techniques in AC, DC, and Hybrid AC–DC Microgrid: A Review. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 738–759. [Google Scholar] [CrossRef]
- Al-Tameemi, Z.H.A.; Lie, T.T.; Foo, G.; Blaabjerg, F. Control Strategies of DC Microgrids Cluster: A Comprehensive Review. Energies 2021, 14, 7569. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, W.; Zeng, F.; Yang, X. A Review of Control Strategies in DC Microgrid. J. Phys. Conf. Ser. 2018, 1087, 042035. [Google Scholar] [CrossRef]
- Dahale, S.; Das, A.; Pindoriya, N.M.; Rajendran, S. An overview of DC-DC converter topologies and controls in DC microgrid. In Proceedings of the 2017 7th International Conference on Power Systems (ICPS), Pune, India, 21–23 December 2017; pp. 410–415. [Google Scholar] [CrossRef]
- Li, M.; Zhang, D.; Lu, S.; Tang, X.; Phung, T. Differential evolution-based overcurrent protection for DC microgrids. Energies 2021, 14, 5026. [Google Scholar] [CrossRef]
- Augustine, S.; Quiroz, J.E.; Reno, M.J.; Brahma, S. DC Microgrid Protection: Review and Challenges; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2018.
- Dragicevic, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids—Part II: A Review of Power Architectures, Applications, and Standardization Issues. IEEE Trans. Power Electron. 2016, 31, 3528–3549. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Guerrero, J.M.; Sun, K.; Vasquez, J.C.; Teodorescu, R.; Huang, L. Hierarchical control of parallel AC-DC converter interfaces for hybrid microgrids. IEEE Trans. Smart Grid 2014, 5, 683–692. [Google Scholar] [CrossRef] [Green Version]
- Bharath, K.R.; Krishnan Mithun, M.; Kanakasabapathy, P. A review on DC microgrid control techniques, applications and trends. Int. J. Renew. Energy Res. 2019, 9, 1328–1338. [Google Scholar]
- Elavarasan, R.M.; Ghosh, A.; Mallick, T.K.; Krishnamurthy, A.; Saravanan, M. Investigations on performance enhancement measures of the bidirectional converter in PV–wind interconnected microgrid system. Energies 2019, 12, 2672. [Google Scholar] [CrossRef] [Green Version]
- Yaqub, R. Phasor Measurement Unit Assisted Inverter—A Novel Approach for DC Microgrids Performance Enhancement. Electricity 2021, 2, 330–341. [Google Scholar] [CrossRef]
- Sahoo, S.; Mishra, S.; Fazeli, S.M.; Li, F.; Dragicevic, T. A Distributed fixed-Time secondary controller for DC microgrid clusters. IEEE Trans. Energy Convers. 2019, 34, 1997–2007. [Google Scholar] [CrossRef]
- Sechilariu, M.; Wang, B.C.; Locment, F.; Jouglet, A. DC microgrid power flow optimization by multi-layer supervision control. Design and experimental validation. Energy Convers. Manag. 2014, 82, 1–10. [Google Scholar] [CrossRef]
- Karimi, Y.; Oraee, H.; Golsorkhi, M.S.; Guerrero, J.M. Decentralized Method for Load Sharing and Power Management in a PV/Battery Hybrid Source Islanded Microgrid. IEEE Trans. Power Electron. 2017, 32, 3525–3535. [Google Scholar] [CrossRef] [Green Version]
- Sun, K.; Zhang, L.; Xing, Y.; Guerrero, J.M. A distributed control strategy based on DC bus signaling for modular photovoltaic generation systems with battery energy storage. IEEE Trans. Power Electron. 2011, 26, 3032–3045. [Google Scholar] [CrossRef] [Green Version]
- Mingsheng, Z.; Peilei, F.; Hesong, W.; Wenkui, W.; Pengcheng, C. Hierarchical Control Strategy for Microgrid. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018; pp. 1528–1532. [Google Scholar] [CrossRef]
- Shuai, Z.; Fang, J.; Ning, F.; Shen, Z.J. Hierarchical structure and bus voltage control of DC microgrid. Renew. Sustain. Energy Rev. 2018, 82, 3670–3682. [Google Scholar] [CrossRef]
- Meng, L.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M.; Perez, J.R. Modeling and sensitivity analysis of consensus algorithm based distributed hierarchical control for DC microgrids. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 342–349. [Google Scholar] [CrossRef] [Green Version]
- Shafiee, Q.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Hierarchical control for multiple DC-microgrids clusters. In Proceedings of the 2014 IEEE 11th International Multi-Conference on Systems, Signals & Devices (SSD14), Barcelona, Spain, 11–14 February 2014; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Yoshimoto, K.; Nanahara, T.; Koshimizu, G.; Uchida, T. New control method for regulating State-of-Charge of a battery in hybrid wind power/battery energy storage system. In Proceedings of the 2006 IEEE PES Power Systems Conference & Exposition, Atlanta, GA, USA, 29 October–1 November 2006; pp. 1244–1251. [Google Scholar]
- Zhou, Y.; Obeid, H.; Laghrouche, S.; Hilairet, M.; Djerdir, A. Disturbance rejection control strategy of hybrid battery/super capacitors power system based on a single converter. In Proceedings of the 2019 8th International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, 3–6 November 2019; pp. 534–539. [Google Scholar] [CrossRef]
- Faria, J.; Pombo, J.; Calado, M.D.R.; Mariano, S. Power Management Control Strategy Based on Artificial Neural Networks for Standalone PV Applications with a Hybrid Energy Storage System. Energies 2019, 12, 902. [Google Scholar] [CrossRef] [Green Version]
- Sathishkumar, R.; Kollimalla, S.K.; Mishra, M.K. Dynamic energy management of micro grids using battery super capacitor combined storage. In Proceedings of the 2012 Annual IEEE India Conference (INDICON), Kochi, India, 7–9 December 2012; pp. 1078–1083. [Google Scholar] [CrossRef]
- Kollimalla, S.K.; Mishra, M.K.; Narasamma, N.L. Design and analysis of novel control strategy for battery and supercapacitor storage system. IEEE Trans. Sustain. Energy 2014, 5, 1137–1144. [Google Scholar] [CrossRef]
- Cabrane, Z.; Kim, J.; Yoo, K.; Ouassaid, M. HESS-based photovoltaic/batteries/supercapacitors: Energy management strategy and DC bus voltage stabilization. Sol. Energy 2021, 216, 551–563. [Google Scholar] [CrossRef]
- Dong, B.; Li, Y.; Zheng, Z.; Xu, L. Control strategies of microgrid with hybrid DC and AC buses. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011. [Google Scholar]
- Gao, F.; Kang, R.; Cao, J.; Yang, T. Primary and secondary control in DC microgrids: A review. J. Mod. Power Syst. Clean Energy 2019, 7, 227–242. [Google Scholar] [CrossRef] [Green Version]
- Keshta, H.E.; Saied, E.M.; Malik, O.P.; Bendary, F.M.; Ali, A.A. Fuzzy PI controller-based model reference adaptive control for voltage control of two connected microgrids. IET Gener. Transm. Distrib. 2021, 15, 602–618. [Google Scholar] [CrossRef]
- Singh, P.; Lather, J.S. A PWM-based sliding mode voltage control of DC-DC boost converter for DC microgrid. In Proceedings of the 2018 IEEE 8th Power India International Conference (PIICON), Kurukshetra, India, 10–12 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Kumaravel, S.; Ashok, S. Adapted multilayer feedforward ANN based power management control of solar photovoltaic and wind integrated power system. In Proceedings of the IEEE PES Innovative Smart Grid Technologies—India (ISGT India), Kollam, India, 1–3 December 2011; pp. 223–228. [Google Scholar] [CrossRef]
- Kumar, T.P.; Subrahmanyam, N.; Sydulu, M. CMBSNN for Power Flow Management of the Hybrid Renewable Energy—Storage System-Based Distribution Generation. IETE Tech. Rev. 2019, 36, 303–314. [Google Scholar] [CrossRef]
- Singh, P.; Lather, J.S. Artificial neural network-based dynamic power management of a DC microgrid: A hardware-in-loop real-time verification. Int. J. Ambient Energy 2020, 43, 1730–1738. [Google Scholar] [CrossRef]
- Singh, P.; Lather, J.S. Accurate power-sharing, voltage regulation, and SOC regulation for LVDC microgrid with hybrid energy storage system using artificial neural network. Int. J. Green Energy 2020, 17, 756–769. [Google Scholar] [CrossRef]
- Kamboj, V.K. A novel hybrid PSO–GWO approach for unit commitment problem. Neural Comput. Appl. 2016, 27, 1643–1655. [Google Scholar] [CrossRef]
- Gao, Z.-M.; Zhao, J. An improved Grey Wolf Optimization algorithm with variable weights. Comput. Intell. Neurosci. 2019, 2019, 2981282. [Google Scholar] [CrossRef]
- Hu, P.; Pan, J.-S.; Chu, S.-C. Improved Binary Grey Wolf Optimizer and Its application for feature selection. Knowl.-Based Syst. 2020, 195, 105746. [Google Scholar] [CrossRef]
- Liu, J.; Wei, X.; Huang, H. An improved Grey Wolf Optimization Algorithm and Its Application in Path Planning. IEEE Access 2021, 9, 121944–121956. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Lin, Q.; Mao, W.; Liu, S.; Dou, Z.; Liu, G. Hybrid Particle Swarm and Grey Wolf Optimizer and its application to clustering optimization. Appl. Soft Comput. 2021, 101, 107061. [Google Scholar] [CrossRef]
- Singh, N.; Singh, S.B. Hybrid Algorithm of Particle Swarm Optimization and Grey Wolf Optimizer for Improving Convergence Performance. J. Appl. Math. 2017, 2017, 2030489. [Google Scholar] [CrossRef]
- Shaheen, M.A.; Hasanien, H.M.; Alkuhayli, A. A novel hybrid GWO-PSO optimization technique for optimal reactive power dispatch problem solution. Ain Shams Eng. J. 2021, 12, 621–630. [Google Scholar] [CrossRef]
- Şenel, F.A.; Gökçe, F.; Yüksel, A.S.; Yiğit, T. A novel hybrid PSO–GWO algorithm for optimization problems. Eng. Comput. 2019, 35, 1359–1373. [Google Scholar] [CrossRef]
- Al-Tameemi, Z.H.A.; Lie, T.T.; Foo, G.; Blaabjerg, F. Optimal Power Sharing in DC Microgrid under Load and Generation Uncertainties Based on GWO Algorithm. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Brisbane, Australia, 5–8 December 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Xu, Q.; Xu, Y.; Xu, Z.; Xie, L.; Blaabjerg, F. A Hierarchically Coordinated Operation and Control Scheme for DC Microgrid Clusters under Uncertainty. IEEE Trans. Sustain. Energy 2021, 12, 273–283. [Google Scholar] [CrossRef]
- Shafiee, Q.; Dragičević, T.; Vasquez, J.C.; Guerrero, J.M. Hierarchical control for multiple DC-microgrids clusters. IEEE Trans. Energy Convers. 2014, 29, 922–933. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Chen, W.; Li, Q.; Yang, H.; Zare, F.; Zheng, Y. Two-level energy management strategy for PV-Fuel cell-battery-based DC microgrid. Int. J. Hydrogen Energy 2019, 44, 19395–19404. [Google Scholar] [CrossRef]
- Cai, H.; Xiang, J.; Wei, W.; Chen, M.Z.Q. Droop Control for PV Sources in DC Microgrids. IEEE Trans. Power Electron. 2018, 33, 7708–7720. [Google Scholar] [CrossRef]
- Jayachandran, M.; Ravi, G. Predictive power management strategy for PV/battery hybrid unit based islanded AC microgrid. Int. J. Electr. Power Energy Syst. 2019, 110, 487–496. [Google Scholar] [CrossRef]
- Mendis, N.; Muttaqi, K.M.; Perera, S. Management of battery-supercapacitor hybrid energy storage and synchronous condenser for isolated operation of PMSG based variable-speed wind turbine generating systems. IEEE Trans. Smart Grid 2014, 5, 944–953. [Google Scholar] [CrossRef]
- Behera, P.K.; Pattnaik, M. Design and Control of DC–DC Converters in a PV-Based LVDC Microgrid. In DC—DC Converters for Future Renewable Energy Systems; Springer: Singapore, 2022; pp. 1–29. [Google Scholar]
- Zammit, D.; Staines, C.S.; Apap, M.; Micallef, A. Control of Buck and Boost Converters for Stand-Alone DC Microgrids. In Proceedings of the Eighth International Symposium on Energy, Aberdeen, Scotland, 24–27 June 2018. [Google Scholar]
- Almabrok, A.; Psarakis, M.; Dounis, A. Fast tuning of the PID controller in an HVAC system using the Big Bang–Big Crunch Algorithm and FPGA technology. Algorithms 2018, 11, 146. [Google Scholar] [CrossRef] [Green Version]






| Controller | Kp | Ki |
|---|---|---|
| PI controller 1 | 10 | 200 |
| Battery controller | 50 | 166.4 |
| SC controller | 80 | 350 |
| Voltage controller (PV) | 4.2956 | 0.6284 |
| Current controller (PV) | 100 | 250 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Tameemi, Z.H.A.; Lie, T.T.; Foo, G.; Blaabjerg, F. Optimal Coordinated Control of DC Microgrid Based on Hybrid PSO–GWO Algorithm. Electricity 2022, 3, 346-364. https://doi.org/10.3390/electricity3030019
Al-Tameemi ZHA, Lie TT, Foo G, Blaabjerg F. Optimal Coordinated Control of DC Microgrid Based on Hybrid PSO–GWO Algorithm. Electricity. 2022; 3(3):346-364. https://doi.org/10.3390/electricity3030019
Chicago/Turabian StyleAl-Tameemi, Zaid Hamid Abdulabbas, Tek Tjing Lie, Gilbert Foo, and Frede Blaabjerg. 2022. "Optimal Coordinated Control of DC Microgrid Based on Hybrid PSO–GWO Algorithm" Electricity 3, no. 3: 346-364. https://doi.org/10.3390/electricity3030019
APA StyleAl-Tameemi, Z. H. A., Lie, T. T., Foo, G., & Blaabjerg, F. (2022). Optimal Coordinated Control of DC Microgrid Based on Hybrid PSO–GWO Algorithm. Electricity, 3(3), 346-364. https://doi.org/10.3390/electricity3030019








