Investigating Various Severity Factor Behaviors for Operational Risk Assessment
Abstract
:1. Introduction
- Four different severity factor definitions are proposed, quantifying four different impacts of a contingency on the transmission system: extreme loading; overvoltage; undervoltage; and voltage instability. A general formulation is given, and for three of the four definitions, a numerical threshold is proposed.
- The operational risk is calculated and analyzed for these four definitions, using a commonly used test system, the IEEE 39-Bus New England system, under varying operating conditions.
- The behavior of the severity factor for individual contingencies is compared with the behavior of the operational risk index for the system as a whole, for increasing system loading. It is shown that multiple definitions of severity factor, and thus of operational risk indices, are needed to obtain a complete picture of the operational security of a transmission system.
2. Operational Risk Calculation
2.1. Operational Risk Procedural Flow
- The computation of probability of contingency, .
- The quantification of severity factor, .
2.2. Probability of Contingency
- Component Unavailability Model
- 2.
- Contingency Definition
2.3. Severity Factors
- Severity factor for overvoltage.
- Severity factor for undervoltage.
- Severity factor for extreme loading.
- Severity factor for system collapse.
2.4. Reliability and Operational Risk Indices
2.5. Case Study
3. Designing of Technical Severity Factors and Their Thresholds
3.1. Alternative Severity Factors
- Technical severity factors, quantifying the impact of a contingency in terms of voltage, current, power, etc., in the transmission grid.
- Economic severity factors, quantifying the contingency impact in terms of financial consequences for the grid owner and/or the customers.
- Customer severity factors, quantifying the contingency impact on the customers, e.g., to quantify the number of customers affected by the contingency.
3.2. Attributes of Severity Factor
- The SF should represent the consequences of a certain contingency.
- The SF should be understandable physically in the grid.
- The SF should be deterministic, and it should show the degree of violation.
- The voltage should be within a certain band.
- The current or loading of the equipment should be below a certain maximum permissible value.
- The system should be voltage-stable. The severity factor is calculated for steady-state analysis.
3.3. Mathematical Formulation of Undervoltage Severity Factor
3.4. Mathematical Formulation of Overvoltage Severity Factor
3.5. Mathematical Formulation of Extreme-Loading Severity Factor
3.6. Mathematical Formulation of System Collapse Severity Factor
4. System-Level Operational Risk Behavior under Varying Operating Conditions
4.1. Operational Risk of Extreme Loading (OREL) Behavior under Varying Operating Conditions
4.2. Operational Risk of Overvoltage (OROV) Behavior under Varying Operating Conditions
4.3. Operational Risk of Undervoltage (ORUV) Behavior under Varying Operating Conditions
4.4. Operational Risk of System Collapse (ORSC) Behavior
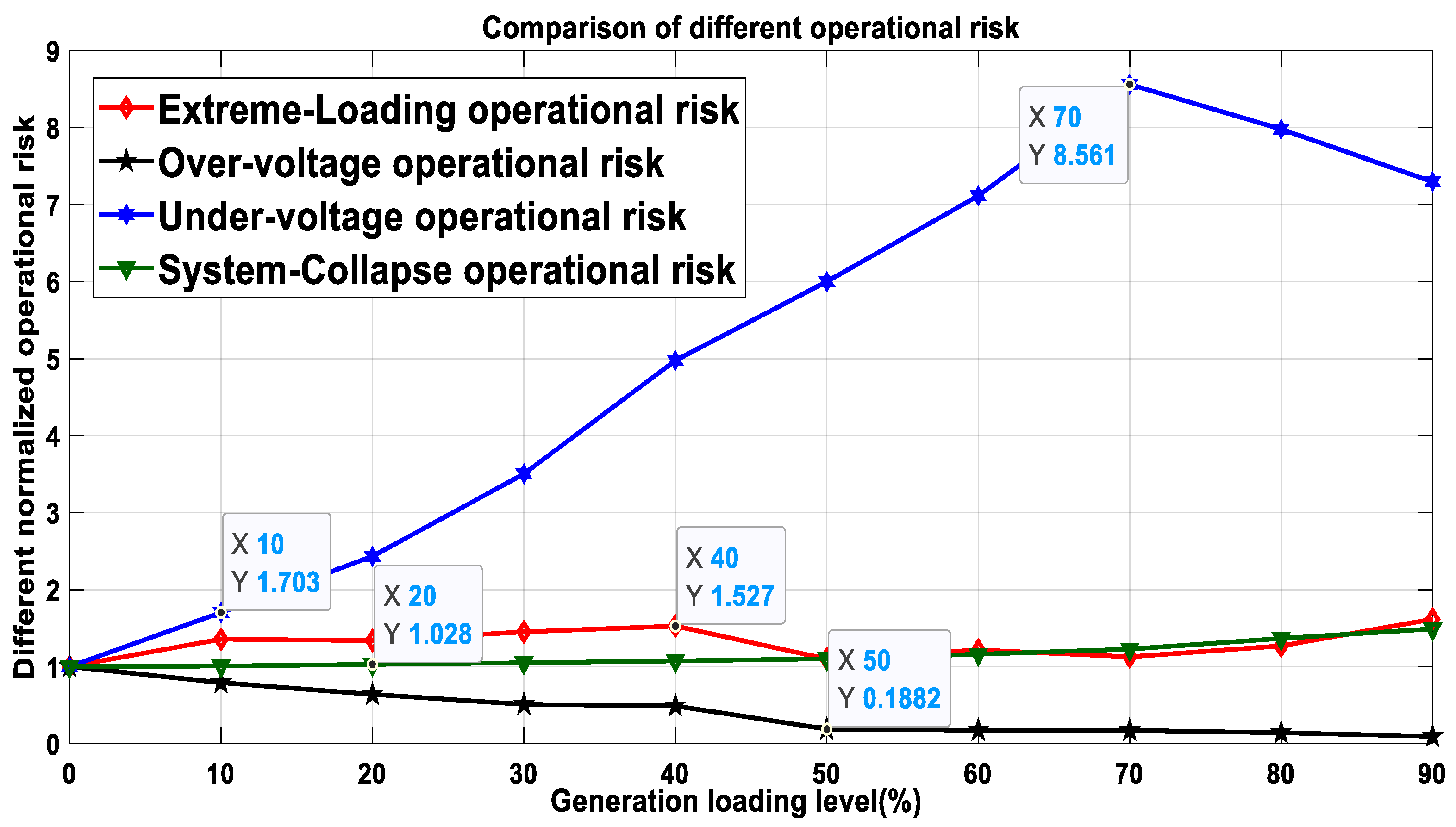
4.5. Interrelation between Various System-Level Operational Risks
5. Further Analysis of Severity Factor Behavior under Varying Operating Conditions
5.1. Operational Risk of Extreme Loading Severity Factor Behavior
5.2. Operational Risk of Undervoltage Severity Factor Behavior
5.3. Operational Risk of Overvoltage Severity Factor Behavior
5.4. Operational Risk of System Collapse Severity Factor Behavior
6. Discussion
6.1. Technical Severity Factor
6.2. Customer Severity Factor
6.3. Economic Severity Factor
6.4. Standardization of Severity Factors
6.5. Additional Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Billinton, R.; Bollinger, K.E. Transmission System Reliability Evaluation Using Markov Processes. IEEE Trans. Power Appar. Syst. 1968, PAS-87, 538–547. [Google Scholar] [CrossRef]
- Mallard, S.A.; Thomas, V.C. A Method for Calculating Transmission System Reliability. IEEE Trans. Power Appar. Syst. 1968, PAS-87, 824–834. [Google Scholar] [CrossRef]
- Billinton, R.; Allan, R.N. Reliability Assessment of Large Electric Power Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Billinton, R.; Allan, R. Reliability Evaluation of Power Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Endrenyi, J. Reliability Modelling in Electric Power Systems; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Choi, J.; Tran, T.T.; El-Keib, A.A.; Thomas, R.J.; Oh, H.; Billinton, R. A method for transmission system expansion planning considering probabilistic reliability criteria. IEEE Trans. Power Syst. 2005, 20, 1606–1615. [Google Scholar] [CrossRef]
- Rei, A.M.; da Silva, A.M.L.; Jardim, J.; Mello, J.C.O. Static and dynamic aspects in bulk power system reliability evaluations. IEEE Trans. Power Syst. 2000, 15, 189–195. [Google Scholar] [CrossRef]
- Billinton, R. Composite System Reliability Evaluation. IEEE Trans. Power Appar. Syst. 1969, PAS-88, 276–281. [Google Scholar] [CrossRef]
- Singh, C.; Mitra, J. Composite system reliability evaluation using state space pruning. IEEE Trans. Power Syst. 1997, 12, 471–479. [Google Scholar] [CrossRef]
- Urgun, D.; Chanan, S. A Hybrid Monte Carlo Simulation and Multi Label Classification Method for Composite System Reliability Evaluation. IEEE Trans. Power Syst. 2019, 34, 908–917. [Google Scholar] [CrossRef]
- Peng, L.; Hu, B.; Xie, K.; Tai, H.M.; Ashenayi, K. Analytical model for fast reliability evaluation of composite generation and transmission system based on sequential Monte Carlo simulation. Int. J. Electr. Power Energy Syst. 2019, 109, 548–557. [Google Scholar] [CrossRef]
- Ramezanzadeh, S.P.; Mirzaie, M.; Shahabi, M. Reliability assessment of different HVDC transmission system configurations considering transmission lines capacity restrictions and the effect of load level. Int. J. Electr. Power Energy Syst. 2021, 128, 106754. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Bhusal, N.; Benidris, M. A convolutional neural network-based approach to composite power system reliability evaluation. Int. J. Electr. Power Energy Syst. 2021, 135, 107468. [Google Scholar] [CrossRef]
- Jun, Q.; Girgis, A. Optimization of power system reliability level by stochastic programming. Electr. Power Syst. Res. 1993, 26, 87–95. [Google Scholar]
- Edimu, M.; Alvehag, K.; Gaunt, C.T.; Ronald, H. Analyzing the perfromance of a time-dependent probabilistic approaches for bulk network reliability assessment. Electr. Power Syst. Res. 2013, 104, 156–163. [Google Scholar] [CrossRef]
- Heylen, E.; Ovaere, M.; Proost, S.; Deconink, G.; Hertem, D.V. A multi-dimensional analysis of reliability criteria: From deterministic N − 1 to a probabilistic approach. Electr. Power Syst. Res. 2018, 167, 290–300. [Google Scholar] [CrossRef]
- Anstine, L.T.; Burke, R.E.; Casey, J.E.; Holgate, R.; John, R.S.; Stewart, H.G. Application of Probability Methods to the Determination of Spinning Reserve Requirements for the Pennsylvania-New Jersey-Maryland Interconnection. IEEE Trans. Power Appar. Syst. 1963, 82, 726–735. [Google Scholar] [CrossRef]
- Wang, P.; Gao, Z.; Bertling, L. Operational Adequacy Studies of Power Systems With Wind Farms and Energy Storages. IEEE Trans. Power Syst. 2012, 27, 2377–2384. [Google Scholar] [CrossRef]
- Janssen, A. Operating Considerations in Reliability of Modelling of Wind-Assisted Utility Systems. Wind Eng. 1982, 6, 193–205. [Google Scholar]
- Vazquez, M.A.; Kirschen, D.S. Estimating the Spinning Reserve Requirements in Systems with Significant Wind Power Generation Penetration. IEEE Trans. Power Syst. 2009, 24, 114–124. [Google Scholar] [CrossRef]
- Da Silva, A.M.L.L.; Sales, W.S.; Manso, L.A.D.F.; Billinton, R. Long-Term Probabilistic Evaluation of Operating Reserve Requirements With Renewable Sources. IEEE Trans. Power Syst. 2010, 25, 106–116. [Google Scholar] [CrossRef]
- Billinton, R.; Karki, B.; Karki, R.; Ramakrishna, G. Unit Commitment Risk Analysis of Wind Integrated Power Systems. IEEE Trans. Power Syst. 2009, 24, 930–939. [Google Scholar] [CrossRef]
- Bouffard, F.; Galiana, F.D. An electricity market with a probabilistic spinning reserve criterion. IEEE Trans. Power Syst. 2004, 19, 300–307. [Google Scholar] [CrossRef]
- Zhou, Z.; Botterud, A. Dynamic Scheduling of Operating Reserves in Co-Optimized Electricity Markets with Wind Power. IEEE Trans. Power Syst. 2013, 29, 160–171. [Google Scholar] [CrossRef]
- Patton, A. A probability method for bulk power system security assessment: I–basic concepts. IEEE Trans. Power Appar. Syst. 1972, PAS-91, 54–61. [Google Scholar] [CrossRef]
- Patton, A. A probability method for bulk power system security assessment: II–development of probability methods for normally operating components. IEEE Trans. Power Appar. Syst. 1972, PAS-91, 2480–2485. [Google Scholar] [CrossRef]
- Patton, A. A probability method for bulk power system security assessment: III–models for standby generators and field data collection and analysis. IEEE Trans. Power Appar. Syst. 1972, PAS-91, 2486–2493. [Google Scholar] [CrossRef]
- Patton, A. Assessment of the security of operating electric power systems using probability methods. Proc. IEEE 1974, 62, 892–901. [Google Scholar] [CrossRef]
- Singh, C.; Patton, A.; Lago-Gonzalez, A.; Vojdani, A.; Gross, G.; Wu, F.; Balu, N. Operating considerations in reliability modeling of interconnected systems-an analytical approach. IEEE Trans. Power Syst. 1988, 3, 1119–1126. [Google Scholar] [CrossRef]
- Da Silva, A.M.L.; Endrenyi, J.; Wang, L. Integrated treatment of adequacy and security in bulk power system reliability evaluations. IEEE Trans. Power Syst. 1993, 8, 275–285. [Google Scholar] [CrossRef]
- Loparo, K.A.; Malek, F.A. A probabilistic approach to dynamic power system security. IEEE Trans. Circuits Syst. 1990, 37, 787–798. [Google Scholar] [CrossRef]
- Khan, M.; Roy, B. Composite system spinning reserve assessment in interconnected systems. IEEE Proc. Gener. Transm. Distrib. 1995, 142, 305–309. [Google Scholar] [CrossRef]
- Gooi, H.B.; Mendes, D.; Bell, K.; Kirschen, D.S.; Kirschen, D.S. Optimal scheduling of spinning reserve. IEEE Trans. Power Syst. 1999, 14, 1485–1492. [Google Scholar] [CrossRef]
- Da Silva, A.L.; Alvarez, G. Operating reserve capacity requirements and pricing in deregulated markets using probabilistic techniques. IET Gener. Transm. Distrib. 2007, 1, 439–446. [Google Scholar] [CrossRef]
- Zio, E. The future of risk assessment. Reliab. Eng. Syst. Saf. 2018, 177, 176–190. [Google Scholar] [CrossRef]
- Li, W. Risk Assessment of Power Systems Models, Methods and Applications; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Ciapessoni, E.; Cirio, D.; Kjølle, G.; Massucco, S.; Pitto, A.; Sforna, M. Probabilistic Risk-Based Security Assessment of Power Systems Considering Incumbent Threats and Uncertainties. IEEE Trans. Smart Grid 2016, 7, 2890–2903. [Google Scholar] [CrossRef]
- Vefsnmo, H.; Kjølle, G.; Jakobsen, S.H.; Ciapessoni, E.; Cirio, D.; Pitto, A. Risk assessment tool for operation: From threat models to risk indicators. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015. [Google Scholar]
- Li, W.; Korczynski, J. Risk evaluation of transmission system operation modes: Concept, method and application. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting Conference Proceedings (Cat. No.02CH37309), New York, NY, USA, 27–31 January 2002. [Google Scholar]
- Perninge, M.; Söder, L. A Stochastic Control Approach to Manage Operational Risk in Power Systems. IEEE Trans. Power Syst. 2011, 27, 1021–1031. [Google Scholar] [CrossRef]
- Jmii, H.; Meddeb, A.; Chebbi, S. Newton-Raphson Load Flow Method for Voltage Contingency Ranking. In Proceedings of the 2018 15th International Multi-Conference on Systems, Signals & Devices (SSD), Yasmine Hammamet, Tunisia, 19–22 March 2018. [Google Scholar]
- Singh, S.N.; Srivastava, L.; Sharma, J. Fast voltage contingency screening and ranking using cascade neural network. Electr. Power Syst. Res. 2000, 53, 197–205. [Google Scholar] [CrossRef]
- Pandit, M.; Srivastava, L.; Sharma, J. Cascade fuzzy neural network based voltage contingency screening and ranking. Electr. Power Syst. Res. 2003, 67, 143–152. [Google Scholar] [CrossRef]
- Mikolinnas, T.A.; Wollenberg, B. An Advanced Contingency Selection Algorithm. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 608–617. [Google Scholar] [CrossRef]
- Du, Y.; Li, F.; Li, J.; Zheng, T. Achieving 100x Acceleration for N-1 Contingency Screening With Uncertain Scenarios Using Deep Convolutional Neural Network. IEEE Trans. Power Syst. 2019, 34, 3303–3305. [Google Scholar] [CrossRef]
- Kaplunovich, P.; Turitsyn, K. Fast and Reliable Screening of N-2 Contingencies. IEEE Trans. Power Syst. 2016, 31, 4243–4252. [Google Scholar] [CrossRef]
- Almeida, S.A.B.d.; Pestana, R.; Barbosa, F.M. Integration of common cause faults in the operational probabilistic approach. In Proceedings of the 2010 IEEE 11th International Conference on Probabilistic Methods Applied to Power Systems, Singapore, 14–17 June 2010. [Google Scholar]
- Bhuiyan, M.Z.A.; Anders, G.J.; Philhower, J.; Du, S. Review of static risk-based security assessment in power system. IET Cyber-Phys. Syst. Theory Appl. 2019, 4, 233–239. [Google Scholar] [CrossRef]
- Wan, H.; McCalley, J.D.; Vittal, V. Risk Based Voltage Security Assessment. IEEE Trans. Power Syst. 2000, 15, 1247–1254. [Google Scholar] [CrossRef]
- Dai, Y.; McCalley, J.D.; Samra, N.A.; Vittal, V. Annual Risk Assessment for Overload Security. IEEE Trans. Power Syst. 2001, 16, 616–623. [Google Scholar] [CrossRef]
- Feng, Y.; Wu, W.; Zhang, B.; Li, W. Power System Operation Risk Assessment Using Credibility Theory. IEEE Trans. Power Syst. 2008, 23, 1309–1318. [Google Scholar] [CrossRef]
- Ni, M.; McCalley, J.D.; Vittal, V.; Tayyib, T. Online Risk-Based Security Assessment. IEEE Trans. Power Syst. 2003, 18, 258–265. [Google Scholar] [CrossRef]
- Ni, M.; McCalley, J.D.; Vittal, V.; Greene, S.; Ten, C.-W.; Ganugula, V.S.; Tayyib, T. Software Implementation of Online Risk-Based Security Assessment. IEEE Trans. Power Syst. 2003, 18, 1165–1172. [Google Scholar] [CrossRef]
- Jong, M.D.; Papaefthymiou, G.; Palensky, P. A Framework for Incorporation of Infeed Uncertainty in Power System Risk-Based Security Assessment. IEEE Trans. Power Syst. 2017, 33, 613–621. [Google Scholar] [CrossRef]
- Bollen, M.; Nazir, Z. Operational Risk Assessment–Time for a Smarter Look at Reliability for Power Transmission Systems. 2022. Available online: https://smartgrid.ieee.org/bulletins/june-2022/operational-risk-assessment-time-for-a-smarter-look-at-reliability-for-power-transmission-systems (accessed on 20 July 2022).
- Liu, P.Q.; Li, H.-Q.; Du, Y.; Zeng, K. Risk assessment of power system security based on component importance and operation state. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014. [Google Scholar]
- Ciapessoni, E.; Cirio, D.; Grillo, S.; Massucco, S.; Pitto, A.; Silvestro, F. Operational Risk Assessment and control: A probabilistic approach. In Proceedings of the 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenburg, Sweden, 11–13 October 2010. [Google Scholar]
- Winter, W.H. Measuring and reporting overall reliability of bulk electricity systems. In Proceedings of the 1980CIGRE Session, Paris, France, 27 August–4 September 1980. Paper No. 32-15. [Google Scholar]
- Winter, W.H. Disturbance performance of bulk electricity systems. In Proceedings of the 1986 C1GRE Session, Paris, France, 27 August–4 September 1986. Paper No. 37/38/39-02. [Google Scholar]
- Schneider, A.; Raksany, J.; Gunderson, R.; Fong, C.; Roy, B.; Neill, P.M.O.; Silverstein, B. Bulk system reliability-measurement and indices. IEEE Trans. Power Syst. 1989, 4, 829–835. [Google Scholar] [CrossRef]
- 5th CEER Benchmarking Report on the Quality of Electricity Supply. 2005. Available online: https://www.ceer.eu/documents/104400/-/-/0f8a1aca-9139-9bd4-e1f5-cdbdf10c4609 (accessed on 20 July 2022).
- Allan, R. Power system reliability assessment—A conceptual and historical review. Reliab. Eng. Syst. Saf. 1994, 46, 3–13. [Google Scholar] [CrossRef]
- Nazir, Z.; Bollen, M.H. Operational Risk Assessment of Transmission Systems: A review. Int. J. Electr. Power Energy Syst. 2022. submitted. [Google Scholar]
- Cupelli, M.; Cardet, C.D.; Monti, A. Voltage stability indices comparison on the IEEE-39 bus system using RTDS. In Proceedings of the 2012 IEEE International Conference on Power System Technology (POWERCON), Auckland, New Zealand, 30 October–2 November 2012. [Google Scholar]
- Rahmouni, W.; Benasla, L. Transient stability analysis of the IEEE 39-bus power system using gear and block methods. In Proceedings of the 2017 5th International Conference on Electrical Engineering-Boumerdes (ICEE-B), Boumerdes, Algeria, 29–31 October 2017. [Google Scholar]
- Kundur, P. Power System Stability and Control, Toronto; McGraw-Hill: New York, NY, USA, 2022. [Google Scholar]
- IEEE. 1366-2012 IEEE Guide for Electric Power Distribution Reliability Indices; IEEE Standard Association: Piscataway, NJ, USA, 2012. [Google Scholar]
- Song, X.; Wang, Z.; Xin, H.; Gan, D. Risk-based dynamic security assessment under typhoon weather for power transmission system. In Proceedings of the 2013 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Hong Kong, China, 8–11 December 2013. [Google Scholar]
- Pour, M.M.; Taheri, I.; Marzooni, M.H. Assessment of transmission outage Contingencies’ effects on bidding strategies of electricity suppliers. Int. J. Electr. Power Energy Syst. 2020, 120, 106053. [Google Scholar]
- Valle, L.D.; Fantazzini, D.; Giudici, P. Copulae and Operational Risks. Int. J. Risk Assess. Manag. Forthcom. 2006, 9, 238–257. [Google Scholar]
- Giudici, P.; Bilotta, A. Modelling Operational Losses: A Bayesian Approach. Qual. Reliab. Eng. Int. 2004, 20, 407–417. [Google Scholar] [CrossRef]
- Jorion, P. Value at Risk-The New Benchmark for Managing Financial Risk, 3rd ed.; McGraw-Hill Professional: New York, NY, USA, 2007. [Google Scholar]
- IEEE. P1366/D5-IEEE Draft Guide for Electric Power Distribution Reliability Indices; IEEE: Piscataway, NJ, USA, 2022; pp. 1–40. [Google Scholar]







| 40% GLL (5th OC) | 50% GLL (6th OC) | ||||
|---|---|---|---|---|---|
| OREL | ORSC | OREL | ORSC | ||
| 1389 | ✓ | ✖ | 1389 | ✖ | ✓ |
| 537 | ✓ | ✖ | 537 | ✖ | ✓ |
| 414 | ✓ | ✖ | 414 | ✖ | ✓ |
| 1121 | ✓ | ✖ | 1121 | ✖ | ✓ |
| 786 | ✓ | ✖ | 786 | ✖ | ✓ |
| 536 | ✓ | ✖ | 536 | ✖ | ✓ |
| 1331 | ✓ | ✖ | 1331 | ✖ | ✓ |
| 861 | ✓ | ✖ | 861 | ✖ | ✓ |
| 70% GLL | 80% GLL | ||||
|---|---|---|---|---|---|
| ORUV | ORSC | ORUV | ORSC | ||
| 801 | ✓ | ✖ | 801 | ✖ | ✓ |
| 892 | ✓ | ✖ | 892 | ✖ | ✓ |
| 659 | ✓ | ✖ | 659 | ✖ | ✓ |
| 993 | ✓ | ✖ | 993 | ✖ | ✓ |
| 142 | ✓ | ✖ | 142 | ✖ | ✓ |
| 700 | ✓ | ✖ | 700 | ✖ | ✓ |
| 1170 | ✓ | ✖ | 1170 | ✖ | ✓ |
| Contingency Probability | 0.008 | 0.0631 | 0.0378 | 0.0841 | 0.042 | 0.0796 | 0.1055 | 0.0573 | 0.0615 | 0.1849 | 0.114 |
| Contingency Number | 2 | 137 | 377 | 414 | 446 | 537 | 555 | 950 | 952 | 1331 | 1356 |
| Std OC | 123% | 238.90% | 282.00% | 576.10% | 361.10% | 244% | 499% | 383.10% | 273.10% | 254.90% | 358.80% |
| 10% (2nd OC) | 136.40% | 263.90% | 159.50% | 650.50% | 407.70% | 166% | 773.90% | 428.30% | 302.80% | 440.10% | N.C |
| 20% (3rd OC) | 150.10% | 289.50% | 341.40% | 734.20% | 460.80% | 185% | N.C | 477.50% | OV | 494.30% | N.C |
| 30% (4th OC) | 164.40% | 315.90% | 372.20% | 834.50% | 526.60% | 208.20% | N.C | 533.50% | OV, UV | 558.40% | N.C |
| 40% (5th OC) | 179.40% | 343.20% | 403.90% | 987.80% | N.C | 632.50% | N.C | OV, UV | OV, UV | 650.20% | N.C |
| 50% (6th OC) | 204.80% | 1661% | 435.80% | N.C | N.C | N.C | N.C | 870.10% | OV, UV | N.C | N.C |
| 60% (7th OC) | 369.50% | 401.90% | 471.10% | N.C | N.C | N.C | N.C | N.C | 473.60% | N.C | N.C |
| 70% (8th OC) | 403.20% | 434.30% | 508.40% | N.C | N.C | N.C | N.C | N.C | 517% | N.C | N.C |
| 80% (9th OC) | 443.10% | 470.10% | 548.50% | N.C | N.C | N.C | N.C | N.C | 571.40% | N.C | N.C |
| 90% (10th OC) | 403.20% | 434% | 508.40% | N.C | N.C | N.C | N.C | N.C | 517% | N.C | N.C |

| Contingency Probability | 0.0567 | 0.1849 | 0.1002 | 0.103 | 0.1057 | 0.114 | 0.1223 | 0.1528 | 0.1094 | 0.1151 |
| Contingency Number | 891 | 1331 | 1351 | 1352 | 1353 | 1356 | 1359 | 1370 | 1405 | 1407 |
| STD: OC | 1.1642 | 1.3305 | 1.0372 | 0.9891 | 1.1097 | 1.6016 | 1.159 | 1.3767 | 1.1555 | 1.017 |
| 10%GLL (2nd OC) | 1.3363 | 1.6962 | 1.5358 | 1.2538 | 1.6033 | N.C | 1.4345 | 2.3204 | 1.8285 | 2.7823 |
| 20%GLL (3rdOC) | 1.557 | 2.0903 | N.C | 1.7328 | N.C | N.C | 1.848 | 3.7776 | 2.8812 | N.C |
| 30%GLL (4th OC) | 1.8683 | 2.6369 | N.C | N.C | N.C | N.C | 2.3334 | N.C | N.C | N.C |
| 40%GLL (5th OC) | 2.47 | 3.8621 | N.C | N.C | N.C | N.C | 3.387 | N.C | N.C | N.C |
| 50%GLL (6th OC) | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C |
| 60%GLL (7th OC) | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C |
| 70%GLL (8th OC) | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C |
| 80%GLL (9th OC) | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C |
| 90%GLL (10th OC) | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C | N.C |

| Contingency Probability | 0.05 | 0.0107 | 0.0569 | 0.0225 | 0.0236 | 0.0268 | 0.1402 | 0.1459 | 0.1204 | 0.073 | 0.0818 | 0.0924 |
| Contingency Number | 56 | 77 | 130 | 229 | 230 | 233 | 875 | 878 | 980 | 1015 | 1019 | 1190 |
| STD (OC) | 0.0605 | 0.0729 | 0.0617 | 0.0958 | 0.133 | 0.0631 | 0.0863 | 0.0658 | 0.0801 | 0.1017 | 0.0912 | 0.0752 |
| 10%GLL (2nd OC) | 0.0597 | 0.0682 | 0.0567 | 0.0337 | 0.1196 | 0.0595 | 0.0859 | 0.0636 | 0.0849 | 0.1071 | 0.0867 | 0.079 |
| 20%GLL (3rd OC) | 0.0583 | 0.0571 | 0.0518 | 0.0209 | 0.0374 | 0.0451 | 0.0813 | 0.0466 | 0.0852 | 0.1132 | 0.0884 | 0.0835 |
| 30%GLL (4th OC) | 0.0563 | 0.0528 | 0.0522 | 0.0046 | 0.0276 | 0.0452 | 0.0279 | 0.044 | 0.0908 | 0.1201 | 0.0689 | 0.0893 |
| 40% GLL (5th OC) | 0.0535 | 0.0417 | 0.0525 | 0.0039 | 0.0069 | 0.0453 | 0.0177 | 0.0438 | 0.0972 | 0.1278 | 0.0696 | 0.0957 |
| 50%GLL (6th OC) | 4.80 × 10−2 | 3.98 × 10−9 | 8.02 × 10−10 | 3.44 × 10−9 | 0.0073 | 1.22 × 10−9 | 0.0198 | 3.44 × 10−10 | 0.0803 | 0.1371 | 0.0057 | 0.1124 |
| 60% GLL (7th OC) | 2.47 × 10−2 | 4.73 × 10−9 | 2.14 × 10−9 | 2.14 × 10−9 | 2.14 × 10−9 | 1.67 × 10−9 | 2.14 × 10−9 | 2.14 × 10−9 | 5.99 × 10−2 | 0.1462 | 1.49 × 10−8 | 1.12 × 10−1 |
| 70% GLL(8th OC) | 1.96 × 10−2 | 6.61 × 10−9 | 6.78 × 10−9 | 6.77 × 10−9 | 6.79 × 10−9 | 6.06 × 10−9 | 6.79 × 10−9 | 6.76 × 10−9 | 6.27 × 10−2 | 0.1571 | 2.58 × 10−8 | 5.26 × 10−2 |
| 80% GLL (9th OC) | 1.43 × 10−8 | 5.30 × 10−8 | 2.13 × 10−8 | 2.14 × 10−8 | 2.13 × 10−8 | 2.03 × 10−9 | N.C | 2.13 × 10−8 | 2.14 × 10−8 | N.C | 4.12 × 10−8 | 5.66 × 10−2 |
| 90%GLL (10th OC) | 6.57 × 10−8 | 6.61 × 10−8 | 6.60 × 10−8 | N.C | 6.40 × 10−8 | 6.44 × 10−9 | N.C | 6.58 × 10−8 | 6.61 × 10−8 | N.C | 5.57 × 10−8 | 6.13 × 10−2 |

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazir, Z.; Bollen, M.H.J. Investigating Various Severity Factor Behaviors for Operational Risk Assessment. Electricity 2022, 3, 325-345. https://doi.org/10.3390/electricity3030018
Nazir Z, Bollen MHJ. Investigating Various Severity Factor Behaviors for Operational Risk Assessment. Electricity. 2022; 3(3):325-345. https://doi.org/10.3390/electricity3030018
Chicago/Turabian StyleNazir, Zunaira, and Math H. J. Bollen. 2022. "Investigating Various Severity Factor Behaviors for Operational Risk Assessment" Electricity 3, no. 3: 325-345. https://doi.org/10.3390/electricity3030018
APA StyleNazir, Z., & Bollen, M. H. J. (2022). Investigating Various Severity Factor Behaviors for Operational Risk Assessment. Electricity, 3(3), 325-345. https://doi.org/10.3390/electricity3030018






