Symmetrical Components and Sequence Networks Connections for Short-Circuit Faults in Five-Phase Electrical Systems
Abstract
:1. Introduction
2. Classification of Short-Circuit Faults
3. Investigation Methodology
- −
- step 1: write the boundary conditions for the selected type of short-circuit fault assuming no load conditions;
- −
- step 2: derive the symmetrical components of voltage and/or current at fault location, as well as the relevant relationships between them;
- −
- step 3: determine the mathematical constraints imposed on the sequence networks connections by the selected fault;
- −
- step 4: draw the equivalent sequence networks connections diagram based on the mathematical constraints previously determined;
- −
- step 5: check the obtained results using computer simulations.
4. Short-Circuit Analysis in Five-Phase AC Systems
4.1. Single-Phase-to-Ground Fault
4.2. Two-Phase Faults
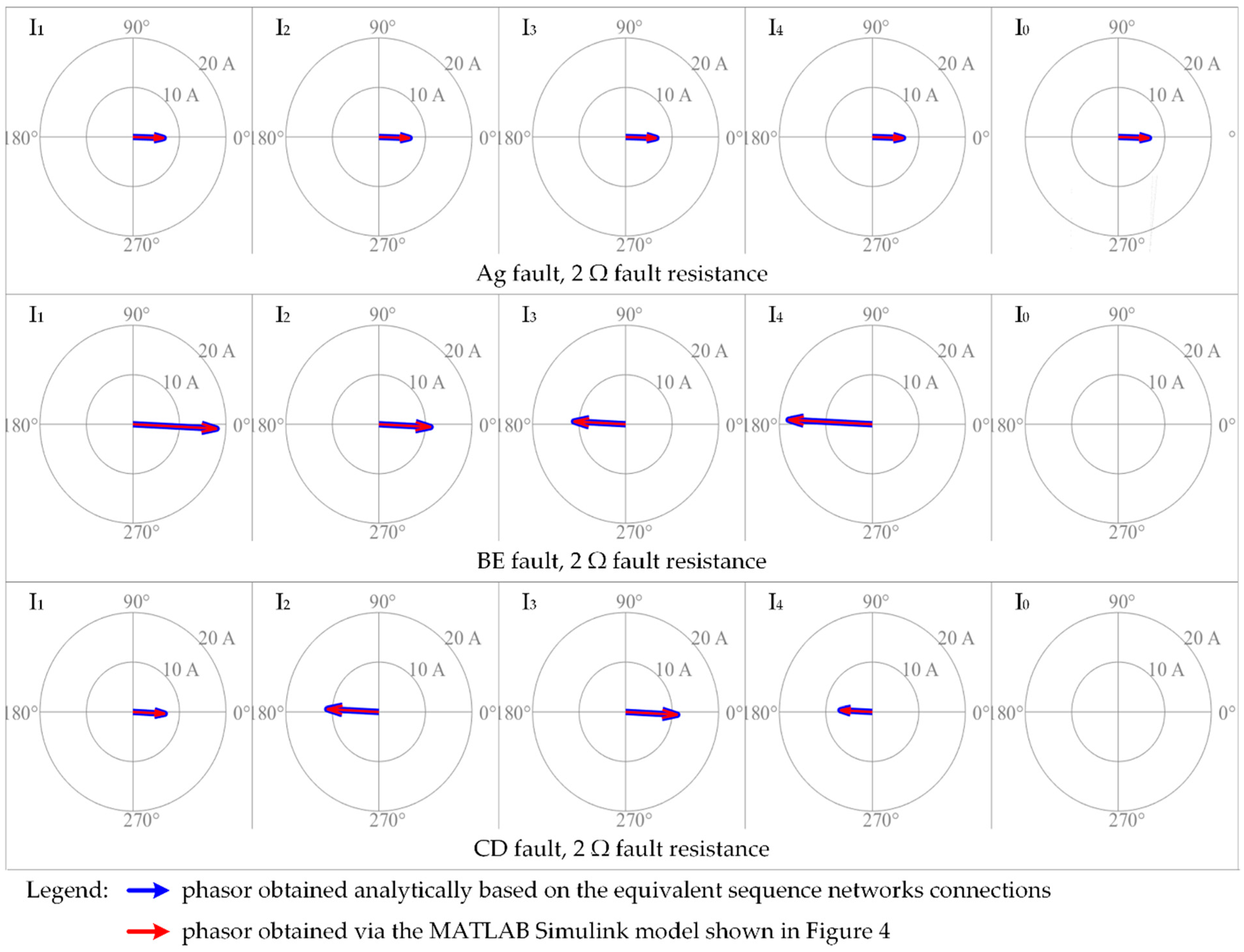
5. Simulation Results
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Blalock, T.J. The first polyphase system. IEEE Power Energy Mag. 2004, 2, 63–66. [Google Scholar] [CrossRef]
- Sekhar, G.C.; Subramanyam, P.S. Protection of Six Phase Transmission system of Allegheny Power System, USA against shunt faults. In Proceedings of the 2014 International Conference on Smart Electric Grid (ISEG), Guntur, India, 19–20 September 2014. [Google Scholar]
- Mustafa, M.W.; Ahmad, M.R.; Shareef, H. Fault analysis on double three-phase to six-phase converted transmission line. In Proceedings of the 2005 International Power Engineering Conference, Singapore, 29 November–2 December 2005. [Google Scholar]
- Ciontea, C.I.; Iov, F. Propagation of voltage sags and under-voltages through Scott transformers. In Proceedings of the 2021 International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & 2021 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Brasov, Romania, 2–4 September 2021. [Google Scholar]
- Abdel-Khalik, A.S.; Shafik, Z.; Elserougi, A.; Ahmed, S.; Massoud, A. A static three-phase to five-phase transformer based on Scott connection. Electr. Power Syst. Res. 2014, 110, 84–93. [Google Scholar] [CrossRef]
- Lanka, K.; Kambhampati, T.; Kumar, V.V.S.B.; Kalyan, M. Three-phase to five-phase transformation using a special transformer connection. Int. J. Appl. Res. Stud. 2012, 1, 1–11. [Google Scholar]
- Tabrez, M.; Sadhu, P.K.; Iqbal, A. A novel three phase to seven phase conversion technique using transformer winding connections. Eng. Technol. Appl. Sci. Res. 2017, 7, 1953–1961. [Google Scholar] [CrossRef]
- Moinoddin, S.; Iqbal, A.; Abu-Rub, H.; Khan, M.R.; Ahmed, S.M. Three-phase to seven-phase power converting transformer. IEEE Trans. Energy Convers. 2012, 27, 757–766. [Google Scholar] [CrossRef]
- Levi, E. Multiphase electric machines for variable-speed applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Cao, W.; Mecrow, B.C.; Atkinson, G.J.; Bennett, J.W.; Atkinson, D.J. Overview of electric motor technologies used for More Electric Aircraft (MEA). IEEE Trans. Ind. Electron. 2012, 59, 3523–3531. [Google Scholar]
- Hezzi, A.; Elghali, S.B.; Salem, Y.B. Control of five-phase PMSM for electric vehicle application. In Proceedings of the 18th International Conference on Sciences and Techniques of Automatic Control & Computer Engineering, Monastir, Tunisia, 21–23 December 2017. [Google Scholar]
- Hakeem, A.A.; Elserougi, A.; Abdel-Khalik, A.S.; Massoud, A.M. Performance of a five-phase boost inverter-fed submersible induction machine. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013. [Google Scholar]
- Liu, H.; Wang, D.; Yi, X. Modeling and analytical calculation of a multiphase induction motor in the phase loss asymmetrical transient process. J. Electr. Eng. Technol. 2019, 14, 1269–1279. [Google Scholar] [CrossRef]
- Dabour, S.M.; Hassan, A.E.W.; Rashad, E.M. Five-phase induction motor drive system fed from five-phase matrix-converter. In Proceedings of the 15th International Middle East Power Systems Conference, Alexandria, Egypt, 23–25 December 2012. [Google Scholar]
- Riveros, J.A.; Barrero, F.; Levi, E.; Durán, M.J.; Jones, M. Variable-speed five-phase induction motor drive based on predictive torque control. IEEE Trans. Ind. Electron. 2013, 60, 2957–2968. [Google Scholar] [CrossRef]
- Gonçalves, P.; Cruz, S.; Mendes, A. Finite control set model predictive control of six-phase asymmetrical machines—An overview. Energies 2019, 24, 4693. [Google Scholar] [CrossRef] [Green Version]
- Che, H.S.; Levi, E.; Jones, M.; Duran, M.J.; Hew, W.P.; Rahim, N.A. Operation of a six-phase induction machine using series-connected machine-side converters. IEEE Trans. Ind. Electron. 2014, 61, 164–176. [Google Scholar] [CrossRef] [Green Version]
- Chinmaya, K.A.; Singh, G.K. An advanced disturbance reduction field-oriented control for six-phase induction machine. In Proceedings of the IEEMA Engineer Infinite Conference, New Delhi, India, 13–14 March 2018. [Google Scholar]
- Mengoni, M.; Zarri, L.; Rizzoli, G.; Tani, A.; Gritli, Y.; Duran, M.J. Use of field harmonics in multiphase induction motor drives for on-line parameter estimation. In Proceedings of the IEEE Workshop on Electrical Machines Design, Control and Diagnosis, Nottingham, UK, 20–21 April 2017. [Google Scholar]
- Liu, X.; Kong, W.; Qu, R.; Xu, Q. Non-sinusoidal power supply technology based on space vector PWM for multiphase variable speed drives. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Portland, OR, USA, 23–27 September 2018. [Google Scholar]
- Umesh, B.S.; Sivakumar, K. Multilevel inverter scheme for performance improvement of pole-phase-modulated Multiphase induction motor drive. IEEE Trans. Ind. Electron. 2016, 63, 2036–2043. [Google Scholar] [CrossRef]
- Levi, E.; Bojoi, R.; Profumo, F.; Toliyat, H.A.; Williamson, S. Multiphase induction motor drives—A technology status review. IET Electr. Power Appl. 2007, 1, 489–516. [Google Scholar] [CrossRef] [Green Version]
- Levi, E. Advances in converter control and innovative exploitation of additional degrees of freedom for multiphase machines. IEEE Trans. Ind. Electron. 2016, 63, 433–448. [Google Scholar] [CrossRef] [Green Version]
- Fortescue, C.L. Method of symmetrical co-ordinates applied to the solution of polyphase networks. In Proceedings of the 34th Annual Convention of the American Institute of Electrical Engineers, Atlantic City, NJ, USA, 19–22 June 1918. [Google Scholar]
- Chicco, G.; Mazza, A. 100 years of symmetrical components. Energies 2019, 12, 450. [Google Scholar] [CrossRef] [Green Version]
- Arafat, A.K.M.; Choi, S.; Baek, J. Open-phase fault detection of a five-phase permanent magnet assisted synchronous reluctance motor based on symmetrical components theory. IEEE Trans. Ind. 2017, 64, 6465–6474. [Google Scholar] [CrossRef]
- Kulkarni, S.; Parit, A.B.; Pulavarthi, B.; Patil, S.S. Comparative analysis of three phase, five phase and six phase symmetrical components with Matlab. In Proceedings of the International Conference on Data Management, Analytics and Innovation, Pune, India, 24–26 February 2017. [Google Scholar]
- Al-Turkki, Y.A. Symmetrical component representation of a six-phase salient-pole machine. J. King Saud Univ.-Eng. Sci. 1993, 5, 17–30. [Google Scholar] [CrossRef]
- Gökalp, E.; Tercan, S.M. Fault analysis in multi-phase power systems considering symmetrical components and chase coordinates methods. J. Eng. Technol. 2019, 3, 41–59. [Google Scholar]
- Prasad Rao, K.P.; Kavya, P.; Sai Kalyan, P. Fault analysis of five phase transmission system. J. Electr. Eng. 2017, 17, 8. [Google Scholar]
- Bhatt, N.B.; Venkata, S.S.; Guyker, W.C.; Booth, W.H. Six-phase (multi-phase) power transmission systems: Fault analysis. IEEE Trans. Power Appar. Syst. 1977, PAS-96, 758–767. [Google Scholar] [CrossRef]
- Abu-Elhaija, W.S.; Amoura, F.K. Fault analysis of six phase power system using six phase symmetrical components. Electr. Power Compon. Syst. 2006, 33, 657–671. [Google Scholar] [CrossRef]
- Ciontea, C.I. The use of symmetrical components in electrical protection. In Proceedings of the 72nd Conference for Protective Relay Engineers, College Station, TX, USA, 25–28 March 2019. [Google Scholar]
- Ciontea, C.I.; Iov, F. A study of load imbalance influence on power quality assessment for distribution networks. Electricity 2021, 2, 77–90. [Google Scholar] [CrossRef]
- Pierre, B.J. High phase order transmission line fault types. Electr. Power Compon. Syst. 2019, 47, 1667–1676. [Google Scholar] [CrossRef] [Green Version]
- Blackburn, J.L. Symmetrical Components for Power Systems Engineering; Marcel Dekker Inc.: New York, NY, USA, 1993. [Google Scholar]
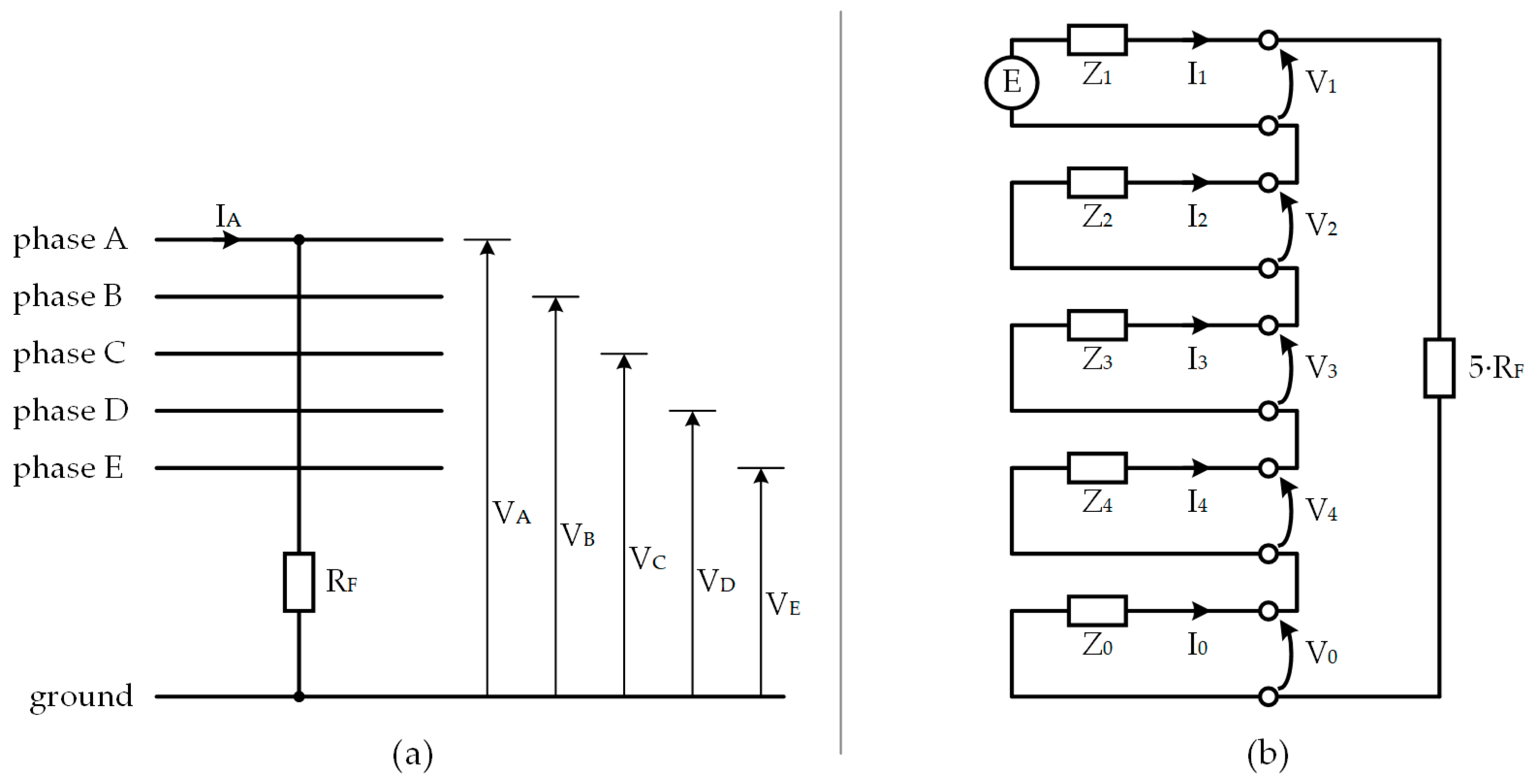
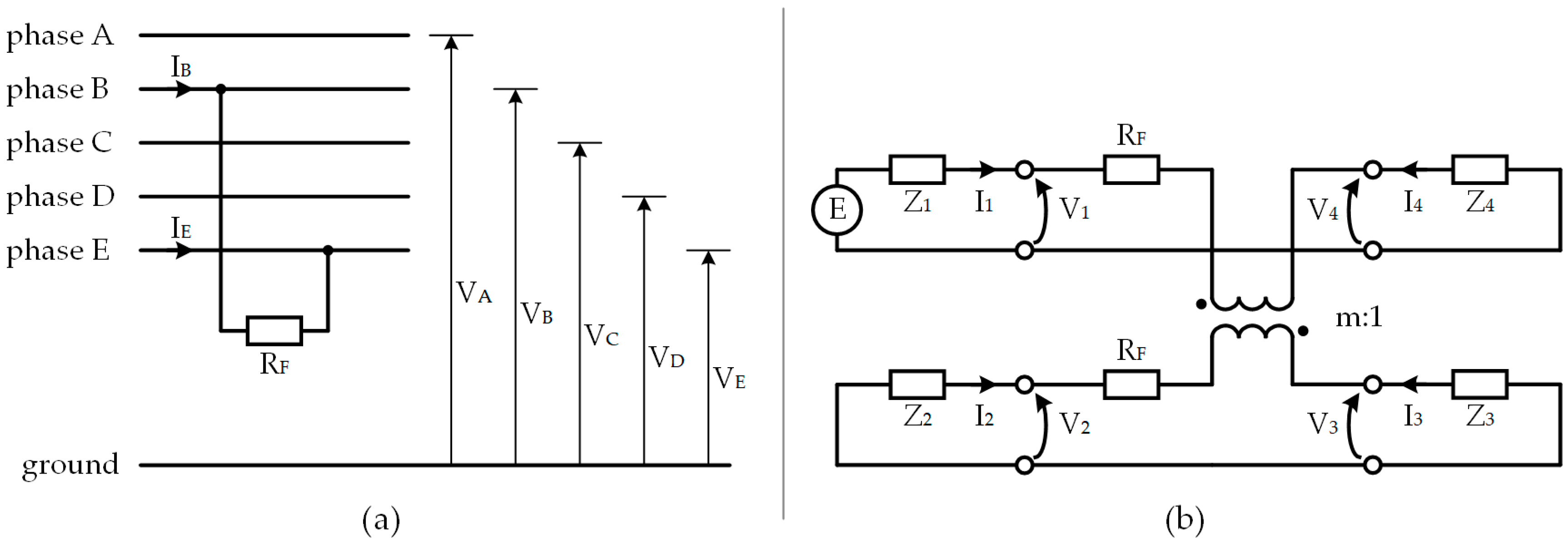
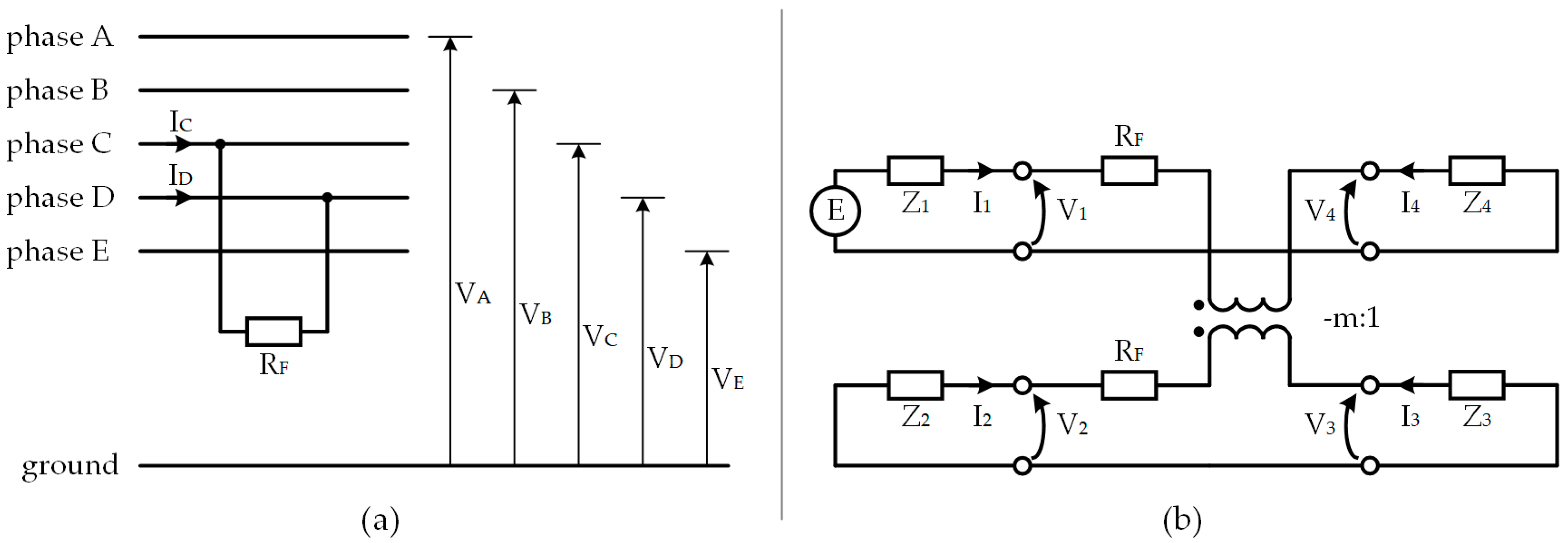

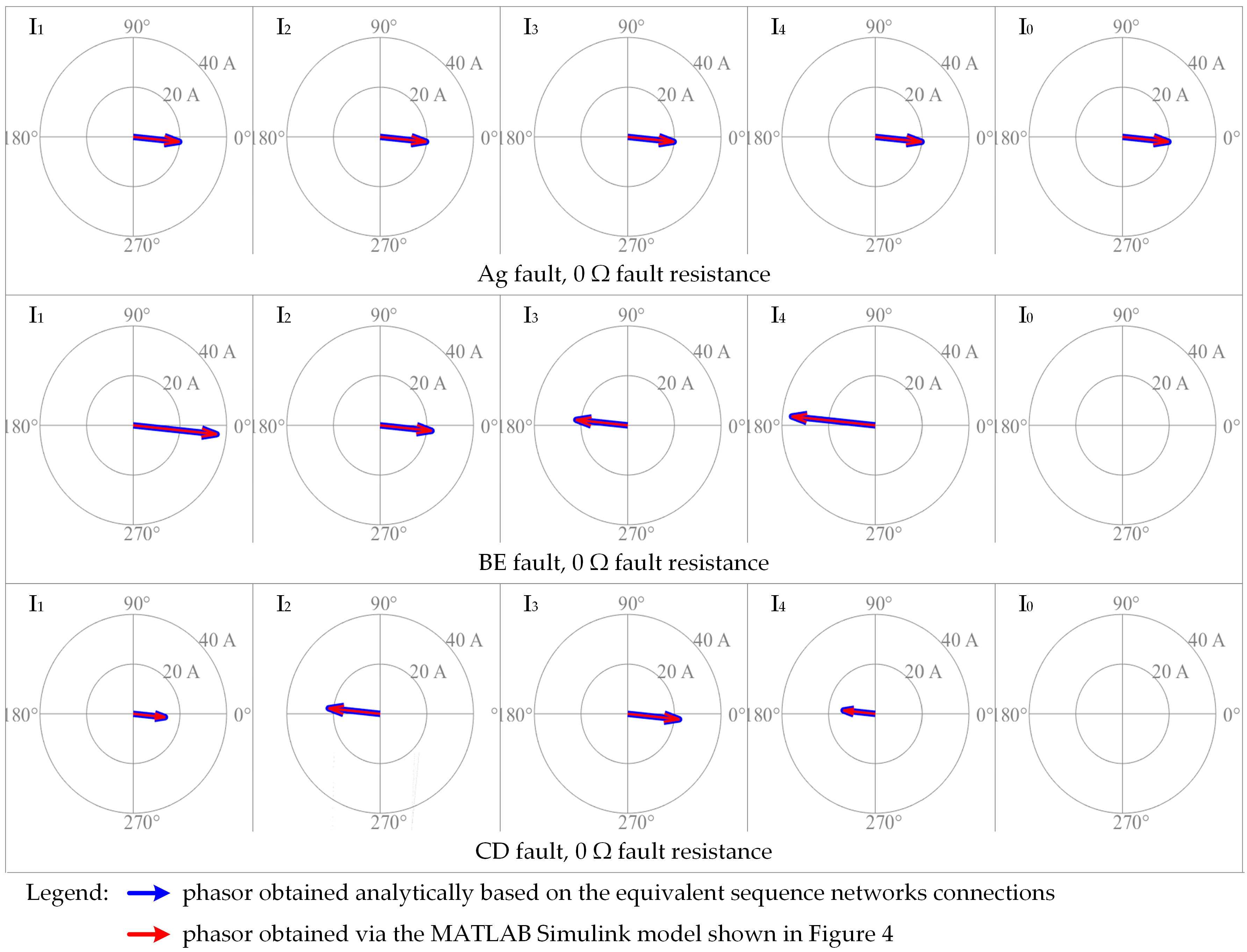

| Fault Type | Short-Circuit Faults in Three-Phase Systems | Short-Circuit Faults in Five-Phase Systems |
|---|---|---|
| Single-phase-to-ground | Ag, Bg, Cg | Ag, Bg, Cg, Dg, Eg |
| Two-phase-to-ground | ABg, ACg, BCg | ABg, ACg, ADg, AEg, BCg, BDg, BEg, CDg, CEg, DEg |
| Two-phase | AB, AC, BC | AB, AC, AD, AE, BC, BD, BE, CD, CE, DE |
| Three-phase-to-ground | ABCg | ABCg, ABDg, ABEg, ACDg, ACEg, ADEg, BCDg, BCEg, BDEg, CDEg |
| Three-phase | ABC | ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDE |
| Four-phase-to-ground | - | ABCDg, ABCEg, ABDEg, ACDEg, BCDEg |
| Four-phase | - | ABCD, ABCE, ABDE, ACDE, BCDE |
| Five-phase-to-ground | - | ABCDEg |
| Five-phase | - | ABCDE |
| Total/significant faults | 11/5 | 57/13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciontea, C.I. Symmetrical Components and Sequence Networks Connections for Short-Circuit Faults in Five-Phase Electrical Systems. Electricity 2022, 3, 251-263. https://doi.org/10.3390/electricity3030015
Ciontea CI. Symmetrical Components and Sequence Networks Connections for Short-Circuit Faults in Five-Phase Electrical Systems. Electricity. 2022; 3(3):251-263. https://doi.org/10.3390/electricity3030015
Chicago/Turabian StyleCiontea, Catalin Iosif. 2022. "Symmetrical Components and Sequence Networks Connections for Short-Circuit Faults in Five-Phase Electrical Systems" Electricity 3, no. 3: 251-263. https://doi.org/10.3390/electricity3030015
APA StyleCiontea, C. I. (2022). Symmetrical Components and Sequence Networks Connections for Short-Circuit Faults in Five-Phase Electrical Systems. Electricity, 3(3), 251-263. https://doi.org/10.3390/electricity3030015






