Abstract
Renewable energy deployment through distributed energy resources is among the central goals of future power systems. Microgrids have proven to be an economically viable solution for distributed energy resources’ integration into the power system and benefits customers with uninterrupted power supply. In this context, provisional microgrids have been introduced with the main goal of rapid renewable energy resource deployment. Since a considerable portion of renewable energy resources, as well as residential loads, are DC, and this portion is expected to grow even further, hybrid AC/DC design of provisional microgrids can improve both efficiency and economic benefit through an optimal arrangement of AC/DC feeders and converters. This paper presents a planning model for hybrid provisional microgrids considering the long-term influence of energy storage and the aging process of converters on economic revenues. Due to several intrinsic uncertainties involved in provisional microgrid operation, robust optimization is applied to the problem to ensure optimality under worst-case conditions. Results show the economic benefits of a hybrid provisional microgrid compared to a provisional microgrid and independent microgrid. Several sensitivity analyses are carried out to identify critical factors in planning.
1. Introduction
Environmental issues and global warming have attracted attention to clean emission-free energy sources [,]. Renewable energy resources (RERs) offer several benefits for both the utility grid and consumers, such as increasing the reliability, decreasing the transmission cost [,], peak shaving [], multifunctionality of areas [], lower carbon footprint [], etc., as well as providing eco-friendly energy []. Microgrids have been among the most intriguing areas of research in power systems during recent years due to the numerous benefits they provide for the grid and streamlining RER integration into the distribution system [,]. Apart from economic advantages, microgrids can improve power quality, alleviate congestion, and increase efficiency in generation and bulk transmission facilities [,,]. As defined the U.S. Department of Energy defines, a microgrid is a set of loads supplied with distributed energy resources (DERs) within clearly defined electrical boundaries []. A microgrid acts as an autonomous entity with respect to the grid and can connect and disconnect from the grid to enable it to operate in both grid-connected and islanded mode. Considering this definition, the most salient feature of microgrids is the ability to self-supply during the islanded mode, which improves the grid’s resiliency against harsh natural disasters that can disrupt the main grid’s supply []. Microgrids can be categorized based on various aspects of design.
One of the most recent points of view categorizes microgrids as AC, DC, or hybrid AC/DC. Traditionally, most microgrids are designed as AC; all loads and DERs are connected to a common AC bus, where DC loads need rectifiers and DC DERs require inverters to be connected to the common AC bus. However, by the expansion of DC-distributed energy resources such as photovoltaic panels and fuel cells and the increasing ratio of DC loads, including EVs in the distribution system, DC microgrids are receiving increasing attention []. In addition, since most electrical energy storage technologies operate with DC electricity, DC microgrid deployment is a viable solution for integrating energy storage into the grid []. Hybrid AC/DC microgrids offer additional benefits, including (1) increased efficiency as a result of extra converter elimination; (2) streamlining the integration of DC renewable energy resources; (3) eliminating the need for synchronizing AC generators [].
Moreover, even components that are not DC based, such as small-scale wind turbines, can benefit from DC microgrids, since they still allow a reduction of the power conversion stages in the interface converter []. The microgrid islanding requirements limit RER deployment, as it enforces that the dispatchable generation capacity exceeds the load. This generation capacity is underutilized most of the time, since the main grid’s electricity benefits from economy of scale, and thus the cost of energy purchase is less than local generation unless the grid is congested or not available []. On the other hand, the high investment cost of renewables discourages microgrid developers from investing in these sources. However, the climate concerns have once again brought forward the benefits of renewable energy resources. To achieve these benefits, a new class of microgrids called provisional microgrids have been proposed, with the main goal of higher penetration of renewable energy resources. In provisional microgrids, the electrical boundaries are clearly defined, and a master controller carries the burden of controlling and operating the available resources, similar to conventional microgrids. On the other hand, provisional microgrids utilize a low percentage of dispatchable units; hence, they cannot handle the islanding by themselves and rely on one or more electrically connected microgrids, known as coupled microgrids. The coupled microgrid is a conventional microgrid with the capability of handling islanding through its dispatchable distributed energy resources. In the case of islanding, the coupled microgrid will supply local loads through its unused capacity. Subsequently, by removing the islanding requirements, the provisional coupled microgrids (PCMGs) could possess a high percentage of renewable energy resources, and therefore, several generation mixes could be chosen []. The stability of provisional coupled microgrids is evaluated and compared to independent microgrids in []. The positive impacts of provisional microgrids on customers and their important role in reliability are investigated in []. A microgrid planning model considering the uncertainty of the renewable generation profile in daily operation is proposed in []. However, microgrids in this paper still conform to the structure of conventional MGs, and each of them includes some dispatchable resources. A comprehensive evaluation of AC/DC hybrid microgrid planning is proposed in []. A cost-efficient optimization algorithm is proposed in [], to optimize the renewable resource operations in a hybrid microgrid given the uncertainty of renewable resources. A suitable decentralized power management strategy for converters, without a communication link between the microgrids, is proposed in [] to achieve power sharing amongst them. It focuses on the topic of back-to-back power electronic converter-based coupled MGs through a three-phase AC interconnecting link. Provisional microgrids can eliminate the need for dispatchable DERs by relying on coupled microgrid generation capacity during islanding through capacity purchase contracts, therefore mitigating the capacity underutilization in adjacent microgrids and ensuring the supply of loads during the islanded mode. One of the most important problems in microgrid planning is the accurate evaluation of benefits provided by the microgrid, which is subject to several uncertainties, including renewable energy unit output forecast, market price forecast, load forecast, islanding state, and availability of converters due to aging. These uncertainties come into even more notice in provisional microgrids, as they rely on non-dispatchable units and the main grid’s supply, which are affiliated with uncertainties. Accurate modeling of the uncertainties and integrating them into the planning model adds considerable complexity to the problem, which is sometimes unnecessary. This paper proposes the idea of hybrid AC/DC microgrids to leverage the profit of renewable energy resources by minimizing the converters’ investment cost and increasing the efficiency of renewable energy generation by removing extra converters. This paper proposes a planning model for provisional hybrid AC/DC microgrids, considering the intrinsic uncertainty of renewable energy resources, market price, load forecast, and availability of converters based on the aging process and maintenance schemes. The optimal generation mix, feeder type, load/RER connection to feeders, and operation schedules are derived. Furthermore, robust optimization is used to address the intrinsic uncertainties of the model, including the generation of renewable energy resources. The main contributions of this article are (1) a new class of microgrids to further leverage the benefits of previously suggested microgrids in efficiently deploying renewable energy resources; (2) incorporating converter aging into the microgrid planning model for more realistic results; (3) illustrating the economic benefit and robustness of the suggested microgrid compared to previously suggested provisional microgrids and independent microgrids using similar parameters; (4) considering reliability issues in the microgrid planning model; (5) evaluating the viability of implementing energy storage in provisional microgrids to enhance operational flexibility. The rest of the paper is organized as follows. The provisional hybrid microgrid planning model is outlined and formulated in Section 2. In Section 3, the problem is decomposed into a master problem and subproblem for computational tractability. Subsequently, the results of numerical simulations on a case study are presented in Section 4. Finally, Section 5 provides a discussion and conclusions.
2. Model Outline
Provisional microgrids have a controller and defined electrical boundaries like microgrids. However, provisional microgrids do not have dispatchable generations of their own, so they should rely on main grid power during grid-connected and the coupled microgrid during islanded hours. During grid-connected hours, the provisional microgrid interacts with the utility grid and sells its excess generation to the grid when the RERs generate more power than demand; it purchases power from the grid when the local generation is not enough to supply local loads. Furthermore, provisional microgrids rely on the utility grid for voltage and frequency regulation during grid-connected hours. During islanded hours, provisional microgrids rely on the coupled microgrid unused capacity for supplying a portion of loads; however, as this generation might be insufficient, the controller may curtail some loads. For this reason, it should be assumed that loads are not critical, as provisional microgrids are considered for residential areas that rarely contain critical loads. As depicted in Figure 1, the provisional microgrid is linked to both the utility grid and coupled microgrid. During normal operation, the provisional microgrid is disconnected from the coupled microgrid and is connected to it only during the islanding mode.
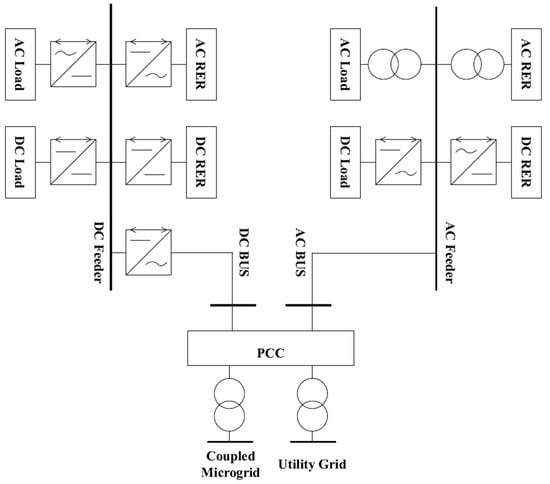
Figure 1.
General configuration of hybrid provisional microgrids.
The reason for this is that during normal operation, if the generation cost of the coupled microgrid is higher than the market price, it would buy its own need from the main grid like the provisional microgrid. In addition, if the generation cost is lower than the market price, it would sell it to the utility grid instead of the provisional microgrid. The same statement is true for the provisional microgrid. The hybrid provisional microgrid contains both AC and DC feeders. AC feeders are connected to a common AC bus. Similarly, DC feeders are connected to a common DC bus, which is connected to the point of common coupling (PCC) alongside the AC bus. PCC links the provisional microgrid to either the utility grid or coupled microgrid. DC RERs are connected to the AC feeder through a DC-to-AC inverter, and DC loads are connected through an AC-to-DC rectifier to a similar feeder. For DC feeders, AC loads are connected via inverters, while a rectifier connects AC RERs to the DC feeder. If the load or RER is the same type as the feeder, they are merely connected by a transformer or converter, as shown in Figure 1. Using separate AC and DC feeders can reduce converter losses (either AC-to-DC or DC-to-AC converters), therefore increasing the efficiency. The aging of converters is a critical factor impacting the economic revenue of the microgrid. Power electronic converters are prone to failure due to fragile components, including electrolytic capacitors and power modules aging over a lifetime that is usually much shorter than the planning horizon []. These devices are not repairable after failure and should be replaced []. Therefore, a preventive maintenance scheme would be the best option for the safe operation of the hybrid microgrid. Several models for evaluating the converter’s reliability have been introduced in the literature, including the Piece-Wise Approach (PWA), Method of Device of Stages (MDS), Semi-Markov Process (SMP), and Markov Chain Technique (MCT) [,,,]. Considering the extra complexity that other methods add to the planning problem, and assuming the preventive maintenance of the power electronic converters, the Piece-Wise Approach (PWA) is used for modeling the availability factor of converters in this paper. Several uncertainties influence the provisional microgrid planning problem, including RER generation, load forecast, market price, and islanding state. The islanding state uncertainty could be simply modeled by a binary variable, which indicates grid-connected mode if it is zero and islanded mode if it is one. For other uncertainties, convex uncertainty sets are assumed to model the uncertainty range as considered in [,]. Different uncertainty limits are considered for aggressive, moderate, and cautious investors to optimize their planning according to different risk levels. The planning model is decomposed into an investment master problem with a long-term timescale and an operation subproblem for shorter timescale scheduling. The robust optimization approach optimizes the problem for worst-case operation conditions considering prevailing uncertainties. The master problem solution determines the RERs and feeder installation state and feeder types (AC or DC) alongside a lower bound of planning costs, while the subproblem yields optimal scheduling for each investment scheme as well as the upper bound. The convergence of the planning problem is checked by the proximity of these bounds. If the problem solution does not converge optimality, cuts are sent back to the master problem to revise the master problem solution. The iterations continue until the optimal solution is obtained. The objective is to minimize total planning costs, which consist of investment cost, operation cost, and reliability cost over the set of primal variables . The costs are converted to present-worth values, and investment costs are annualized to address the equivalent cost for each year during the planning horizon (1). The present-worth coefficient is used to obtain the discounted costs. The optimization is subject to several constraints (Equations (2)–(13)). The problem is formulated based on the provisional microgrid planning model presented in [] and the hybrid AC/DC microgrid model in []:
where:
Subject to:
Investment costs include DC and AC RER investment costs, which are separated in order to attribute inverter costs to DC RERs connected to AC feeders and rectifier costs to AC RERs connected to DC feeders. Similarly, for DC loads connected to the AC feeder and AC loads connected to the DC feeder, rectifier and inverter should be considered, respectively. Finally, the DC bus would need a rectifier and inverter in order to exchange power with the grid (Equation (2)). The operation cost of RERs is assumed as negligible; hence, the operation cost includes the energy purchase from the utility grid during the grid-connected mode and from the coupled microgrid during the islanded mode (Equation (3)). The energy purchase cost is positive if the microgrid imports energy from the grid or coupled microgrid (P is positive) and negative if the microgrid exports energy to the grid or coupled microgrid (P is negative). It should further be noted that the provisional microgrid neither purchases nor sells energy to the coupled microgrid during the grid-connected mode since both microgrids tend to purchase energy from the grid while the market price is lower than the negotiated price and sell their excess generation to the grid when the market price is high. Finally, the reliability cost indicates the cost of load curtailment, which is the Value of Lost Load (VOLL) times the curtailed load (Equation (4)).
The RER connection to feeders is shown by , where the first one indicates the connection to an AC feeder and the latter shows the DC feeder connection. Feeder type is determined by the variable , where implies the feeder is AC; otherwise, the feeder is considered DC. Each RER can be connected to a single feeder; if the RER is connected to none of the feeders, the RER is not installed, and therefore the generation of that specific RER is zero during the planning horizon (Equations (5) and (6)). The RER generation is determined by the forecasted generation as well as the type of feeder they are connected to and the efficiency of the converter joining them (Equations (7) and (8)). The availability coefficient A used in these equations is based on Equations (7) and (8) and is calculated based on the failure and repair rate of power electronic converters according to . A converter could fail due to either random failure or component wear-out. The failure rate increases as the device grows older, as shown in Figure 2. However, this process can be avoided by regular maintenance and component replacement, therefore keeping the failure rate at a constant value.
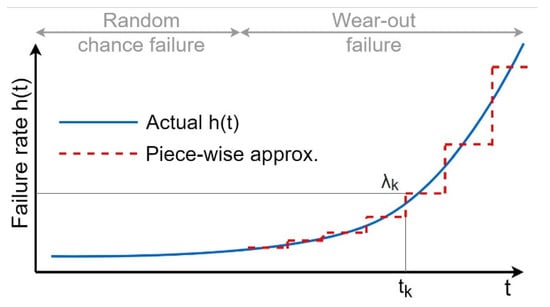
Figure 2.
Failure rate function [].
The power balance of the provisional microgrid and the neighboring microgrids, as well as the main grid, is described in Equation (9), where the total power on the feeders must equal the power transferred from or to the main grid and coupled microgrids. The load and generation equality for each feeder is shown in (Equation (10)), where the summation of RER effective generation plus the power injected from the feeder must be equal to total DC and AC load times the efficiency coefficient of their converters plus the curtailed load.
The provisional microgrid can exchange power with the utility grid or microgrid according to its maximum transfer capacity, which is determined by the loading capacity of the feeders. The power exchange with the utility grid is limited by the capacity of the link between the provisional microgrid and the utility grid during the grid-connected mode. If the connection is disrupted by any means (), power exchange with the utility grid drops to zero, and the provisional microgrid must rely on its own generation and the coupled microgrid’s capacity (Equation (11)). Similarly, as reasoned previously, there is no power exchange with coupled microgrid during the grid-connected mode (), and during the islanded mode, the power exchange with the coupled microgrid is limited by the coupling link’s capacity (Equation (12)). The amount of curtailed load cannot exceed the total load demand as shown in (Equation (13)). This formulation is in accordance with the model outlined in Section 2.
3. Problem Decomposition
There are several uncertainties existing in this optimization problem, including uncertainties prevailing in load forecast, renewable energy generation, and electricity price. In order to handle these uncertainties, two different approaches exist in the literature. Stochastic optimization seeks to find the optimal value for objective function over a discrete set of probable scenarios, while robust optimization optimizes the solution for the worst-case scenario, ensuring that the solution satisfies security constraints over all possible scenarios. While robust optimization yields a more conservative solution compared to stochastic optimization, it is computationally less burdensome. In this paper, we adopt robust optimization for computational efficiency as well as comparability with the results presented for the provisional microgrid in []. Using Bender’s decomposition, the planning problem (Equations (1)–(13)) is decomposed into a master investment problem and an operation subproblem. The master problem presented in Equation (14) seeks to minimize RER and converter capital cost and derive feeder types (AC/DC) over a set of primal variables [].
Subject to: Equations (5) and (6).
The optimality cut (Equation (15)) is initialized at zero and then corrected at each iteration after solving the operation subproblem, updating the optimal generation mix and feeder type for the next iteration.
Master problem solutions are then sent to the operation subproblem to determine the optimal operational variables under the worst-case scenario. The subproblem is the operation problem under the worst-case uncertain values and is formulated as follows:
Subject to: Equations (7)–(13).
The uncertainties in demand, renewable generation, and market price values are modeled using binaries for upper and lower limits of uncertainties as shown in Equations (17)–(19), respectively.
To ensure that upper and lower uncertainties do not coincide, inequality constraints are formulated in Equation (20), allowing only one of the limits to be activated.
The level of robustness can be tailored based on the upper level of uncertainty as formulated in Equations (21)–(24). Choosing a larger upper limit indicates a more conservative investment approach that prefers to take into account more uncertainties by allowing uncertain variables associated with upper and lower uncertainty limits to take the value of one, therefore ensuring the robustness of the solution. More aggressive investors would prefer to reduce investment costs by choosing a lower limit on uncertain variables at the risk of more uncertainties affecting the short-term operation of the microgrid.
The nonlinearities created by the product of binary and continuous variables are resolved by reformulation through adding constraints, including upper and lower limits for continuous variables. After solving the operation subproblem at each iteration, the optimality cut is sent back to the master problem to adjust the investment scheme until the solution converges.
4. Numerical Simulation
A group of electric loads with an annual peak of 8.5 MW along with a set of renewable energy resources including wind and solar units forms a provisional microgrid. A 20-year planning horizon is considered, and load, renewable generation, and market price are forecasted according to historical data from [,,,,]. The annualized investment cost is considered 120,000 $/MW and 180,000 $/MW for wind and solar units, respectively, and nine hours of islanding is assumed during each year. A failure rate of and repair time of 120 h is considered for each power electronic converter in the hybrid microgrid. The connection to the grid has no capacity limit, while the connecting line to coupled microgrid has a capacity limit of 1 MW, assuming a 2000 $/MWh value of lost load and 90 $/MWh negotiated price of coupled microgrid energy. The following cases are modeled in General Algebraic Modeling System (GAMS) and solved with IBM CPLEX 12.6 package on a 2.6 GHz personal computer.
Case 1: Hybrid provisional microgrid planning
Case 2: Sensitivity analysis of the market price
Case 3: Sensitivity analysis of DC load ratio
Case 4: Energy storage installation study
4.1. Case 1
The base case planning problem for the hybrid provisional microgrid is solved with similar data to [] for the sake of comparison. The uncertainty of load forecast is considered 10%, and the uncertainty of market price and renewable generation is assumed as 20%. Single AC and DC feeders are presumed, and the DC load ratio is assumed to be 0.5. The limit on the uncertainty option for load and renewable generation is considered 1000 h/year, while this limit for the market price is set at 2000 h/year. The islanding is limited to nine hours in each planning year. Both wind and solar units will be installed with a total planning cost of $38,458,216, where the investment cost comprises $9,586,821 of the total cost, and $26,173,225 will be spent on purchasing power from the utility grid and coupled microgrid. Load curtailment cost will be $2,698,170 within the 20-year planning horizon. The total planning cost of the provisional microgrid is $40,607,816 [], which is 5.5% higher than the hybrid provisional microgrid total cost, which indicates the economic viability of hybrid provisional microgrids. Furthermore, the total planning cost of a microgrid for the same case is $42,451,534, which is a less economic choice than the latter two choices. A detailed comparison between these schemes is indicated in Figure 3. This comparison clearly demonstrates the economic viability of the hybrid provisional microgrid when compared to the provisional microgrid and microgrid. This is the result of two following benefits of the hybrid provisional microgrid:
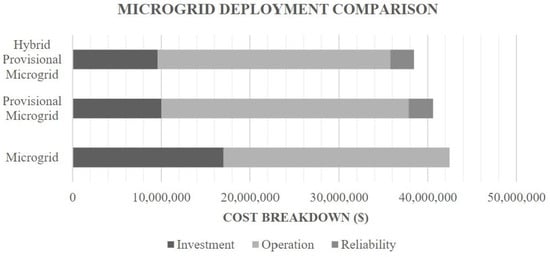
Figure 3.
Microgrid deployment comparison.
- Elimination of investment costs related to surplus electronic power converters.
- Diminishing of operation costs resulting from the elimination of losses due to surplus converters.
However, both provisional and hybrid provisional microgrids incur reliability costs associated with the unsupplied load. This drawback is compensated by cost savings in operational and investment costs. It should be mentioned that provisional microgrids are not suitable for supplying critical loads, and their main goal is to increase the deployment of renewable energy resources in residential areas. This drawback can also be covered with microgrid deployment, which fortifies coupled microgrid supply during peak demand hours.
4.2. Case 2
In order to analyze the impact of market price on the planning problem, first, we changed the market price to within a 20% range of the forecasted price. As can be observed in Figure 4, with the increase in market price, the investors are more inclined to invest in local RERs. Therefore, unlike what it might look at first glance, the investment cost increases and operation cost decreases due to ample generation of RERs, resulting in a reduced tendency to supply power from the grid. Another implication of the cost analysis is that the investors can recover their investment in RERs more rapidly with a higher market price; therefore, this would encourage them to invest in renewable energy resources, thus justifying the economic viability of hybrid provisional microgrids.
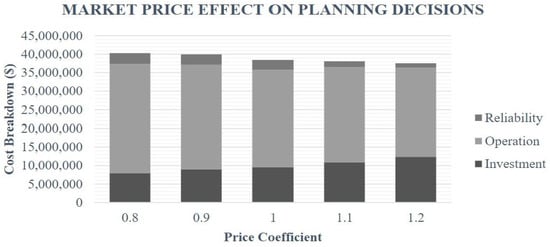
Figure 4.
Market price effect on planning decisions.
To verify the cost of robustness against market price uncertainties, we chose a 10% uncertainty in market price and 2000 h/year uncertainty limit for market price. This modification in the problem results in a total planning cost of $42,451,534, which shows a 9.48% increase compared to case 1. The extra $3,993,318 is spent to ensure the robustness of the microgrid against uncertainties in load, RER generation, and market price. Considering uncertainty in this solution changes the RER mix as well as feeder configuration in the solution. The computational effort is further increased from six iterations until convergence to 10, which means almost double the computational complexity. Although the total cost is higher and the computational complexity increases compared to case 1, this case yields more realistic guidelines for hybrid provisional microgrid investors in choosing the generation mix and feeder configuration as well as a better estimation of the economic benefits of the microgrid in the case of inaccuracies in forecasted price signals.
4.3. Case 3
To evaluate the impact of the DC load ratio on the cost, the DC load ratio is increased from 0.5 (base case) to 1.0. As can be observed in Figure 5, as the DC load ratio increases, the investment cost starts to decrease; the investment cost of inverters is removed because when the DC load ratio is increased, the number of DC feeders increases as well. Furthermore, the operation cost decreases because of inverter coefficient elimination. Therefore, it could be suggested that when the DC load ratio is increased, microgrid developers tend to utilize more DC distributed energy resources, such as PV systems, in order to eliminate inverter coefficient costs. No tangible change can be observed in load shedding cost, since there is no explicit relation between load shedding and DC load ratio. In addition, the PMG relies on the coupled AC microgrid during islanding to meet the demand. In this case, it could be suggested that, during islanding, PMG should provide the demand from DC feeders in the vicinity. Consequently, the total cost changes by 14% as the DC load ratio increases from 0.5 to 1.0. Although the 100% DC load ratio is far from realistic, the case is included for the completeness of calculations.
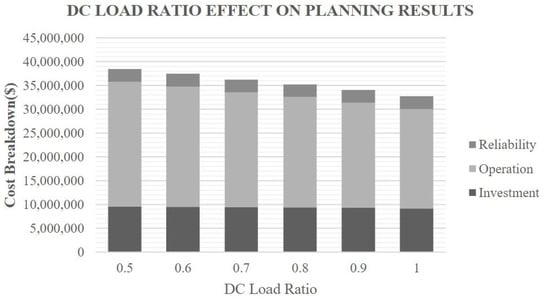
Figure 5.
DC load ratio effect on planning results.
4.4. Case 4
Energy storage systems (ESS) can provide the microgrid with further control over the uncertainties prevailing in RER generation and market price. A hybrid provisional microgrid can benefit more from ESS by optimally allocating them to AC or DC feeders and removing the converters in between. Incorporating ESS in the planning problem requires adjustments to the objective function and operational constraints [].
The investment cost of the objective function (Equation (2)) should be augmented with the energy storage capital cost of energy capacity (CE) and power capacity (CP) as well as the capital cost of the required converter if connected to the different feeder type, which is determined by the energy storage type and feeder type ( is used for DC energy storage and is used for AC energy storage), as formulated in Equation (25).
The constraints described in Equations (26) and (27) ensure that each energy storage is connected to one feeder for each set of AC energy storage () and DC energy storage (). The power balance constraint (Equation (10)) is updated to Equation (28) to account for energy storage charge and discharge as well as the required converter efficiency and aging at each hour of operation.
In order to study the economic viability of installing energy storage systems in the hybrid provisional microgrid, we consider a battery energy storage system (BESS) comparable to the standard energy storage choice used in [], with 1 MW power capacity and 6 MWh energy capacity, and an annualized investment cost of 30,000 $/MWh for energy capacity and 60,000 $/MW for power capacity. Running the planning problem with the same settings as Case 1 gives the results presented in Figure 6.
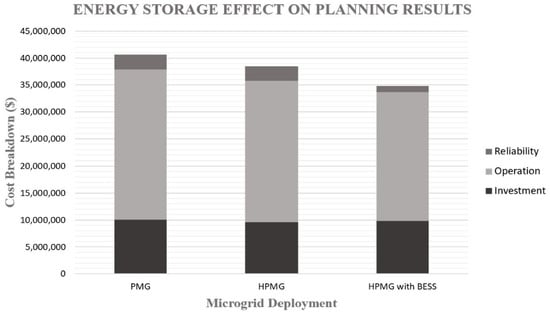
Figure 6.
Energy storage effect on planning results.
As the results show, installing BESS requires $240,000 additional investment costs. However, the expenditure is reimbursed through savings in operational and reliability costs. With the BESS installed, the HPMG is now able to store its excess generation and sell it to the grid at times of higher price. Therefore, the additional revenue from selling energy reduces operational costs by $2,291,589. Additionally, with further control over RER volatility, the reliability cost incurred by load curtailment is now cut by 50%. Altogether, the total planning cost of HPMG is reduced by 9.45% by augmenting it through BESS. This clearly shows the economic viability of this choice, which is the result of the following reasons:
- Storing the surplus generation of DERs and selling it to the main grid.
- Purchasing generation from the main grid during the lower price period and selling it back to the main grid at the time of higher prices.
- Less dependency on higher priced generation by further utilizing stored renewable energy.
5. Discussion and Conclusions
Provisional microgrids provide several benefits for the grid, including increasing renewable DG proliferation, deferring distribution system enhancement, economic benefits, and improved flexibility in the distribution system. Since DC loads such as electric vehicles are increasing, and a considerable proportion of renewable generation like PV panels are DC hybrid, AC/DC can increase both efficiency and economic benefits. This paper proposes upgrading the provisional microgrid to a hybrid AC/DC provisional microgrid to further increase the benefits arising from this class of microgrids. The improvements were indicated by numerical simulations, and the economic viability of this microgrid was shown. According to the results, in the base case, it is shown that the total cost of regular PMGs is 5.5% higher than hybrid PMGs, which illustrates the economic viability of hybrid provisional microgrids. When the market price is diminished, however, both investment and operation costs decrease, but the reliability cost increases, and subsequently, the total price will increase roughly 7% in the case of a 40% decline in market price. Moreover, the investment cost, operation cost, load shedding cost, and consequently the total cost will decrease as well, stay roughly steady and decreasing about 14%, respectively, when the DC load ratio increases from 0.5 to 1. Finally, it is shown that enhancing the HPMG with an energy storage system would further increase economic benefits through additional control over generation volatility and optimal energy transaction with the main grid.
Author Contributions
Conceptualization, O.R., O.M., M.P. and H.G.; data curation, O.R., O.M. and M.P.; formal analysis, O.R., O.M. and M.P.; funding acquisition, H.G.; investigation, O.R., O.M., M.P. and H.G.; methodology, O.R., O.M., M.P. and H.G.; project administration, H.G.; resources, H.G.; software, O.R., O.M. and M.P.; supervision, H.G.; validation, O.R., O.M., M.P. and H.G.; visualization, O.R., O.M., M.P. and H.G.; writing–original draft, O.R., O.M., M.P. and H.G.; writing–review & editing, H.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the University of Stavanger.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This paper was supported by the Department of Safety, Economics, and Planning of the University of Stavanger. Special thanks also go to the Smart City Group and Future Energy Hub at the University of Stavanger for their support.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Index for hour | |
| Superscript for RER generation uncertainty | |
| Index for day | |
| Index for AC RER | |
| Subscript for inverter | |
| Index for DC RER | |
| Index for feeder | |
| Superscript for load uncertainty | |
| Superscript for market price uncertainty | |
| Index for year | |
| Subscript for rectifier |
Parameters
| Availability of power electronic converters | |
| Annualized investment cost of RERs | |
| Annualized investment cost of inverters | |
| Annualized investment cost of rectifiers | |
| Hourly demand | |
| RER rated power | |
| Coupled microgrid link’s flow limit | |
| Feeder maximum loading capacity | |
| Utility grid link’s flow limit | |
| DC load ratio | |
| Present-worth value coefficient | |
| Converter failure rate | |
| Converter repair rate | |
| Converter efficiency | |
| Market price | |
| Coupled microgrid negotiated price | |
| Value of lost load (VOLL) | |
| Uncertainty level limit |
Variables
| Load curtailment | |
| Hourly demand | |
| Set of DC sources | |
| Set of AC sources | |
| Set of energy storage | |
| Storage energy level | |
| RER generation | |
| Power exchange of AC feeder | |
| Power exchange of DC feeder | |
| Power exchange with coupled microgrid | |
| Power exchange with utility grid | |
| Annual operation cost | |
| Binary variable for islanding (0 if islanded) | |
| Binary variable for AC feeder connection (1 if connected) | |
| Binary variable for DC feeder connection | |
| Binary variable for AC feeder | |
| Binary variable for DC feeder | |
| Projected operation cost in investment problem | |
| Dual variables |
References
- Greenhouse Gas (GHG) Emissions. 2018. Available online: https://www.epa.gov/ghgemissions (accessed on 10 March 2022).
- Mirzapour, O.; Sahraei-Ardakani, M. Environmental Impacts of Power Flow Control with Variable-Impedance FACTS. In Proceedings of the 52nd North American Power Symposium (NAPS), Tempe, AZ, USA, 11–14 April 2021. [Google Scholar]
- Savadkouhi, A.F.; Elyasichamazkoti, F.; Fard, M.F. Decentralized Reactive Power Sharing in Autonomous Microgrids. In Proceedings of the 2021 IEEE Electrical Power and Energy Conference (EPEC), Toronto, ON, Canada, 21 October 2021. [Google Scholar]
- Gholami, H.; Røstvik, H.N. Economic Analysis of BIPV Systems as a Building Envelope Material for Building Skins in Europe. Energy 2020, 204, 117931. [Google Scholar] [CrossRef]
- Gholami, H.; Rezaei, O.; Hoseinian, H. Economic Evaluation of Installation and Peak Shaving Using Photovoltaic Systems. In Proceedings of the Emerging Trends in Energy Conservation (ETEC), Tehran, Iran, 2 July 2013. [Google Scholar]
- Gholami, H.; Røstvik, H.N.; Steemers, K. The Contribution of Building-Integrated Photovoltaics (BIPV) to the Concept of Nearly Zero-Energy Cities in Europe: Potential and Challenges Ahead. Energies 2021, 14, 6015. [Google Scholar] [CrossRef]
- Gholami, H.; Røstvik, H.N. Levelised Cost of Electricity (LCOE) of Building Integrated Photovoltaics (BIPV) in Europe, Rational Feed-In Tariffs and Subsidies. Energies 2021, 14, 2531. [Google Scholar] [CrossRef]
- Qazi, A.; Hussain, F.; Rahim, N.A.; Hardaker, G.; Alghazzawi, D.; Shaban, K.; Haruna, K. Towards Sustainable Energy: A Systematic Review of Renewable Energy Sources, Technologies, and Public Opinions. IEEE Access 2019, 7, 63837–63851. [Google Scholar] [CrossRef]
- Adefarati, T.; Bansal, R.C. Reliability, Economic and Environmental Analysis of a Microgrid System in The Presence of Renewable Energy Resources. Appl. Energy 2019, 236, 1089–1114. [Google Scholar] [CrossRef]
- Mirzapour, O.; Arpanahi, S.K. Photovoltaic Parameter Estimation Using Heuristic Optimization. In Proceedings of the IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 22 December 2017. [Google Scholar]
- Talapur, G.G.; Suryawanshi, H.M.; Xu, L.; Shitole, A.B. A Reliable Microgrid with Seamless Transition Between Grid Connected and Islanded Mode for Residential Community with Enhanced Power Quality. IEEE Trans. Ind. Appl. 2018, 54, 5246–5255. [Google Scholar] [CrossRef] [Green Version]
- Parag, Y.; Ainspan, M. Sustainable Microgrids: Economic, Environmental and Social Costs and Benefits of Microgrid Deployment. Energy Sustain. Dev. 2019, 52, 72–81. [Google Scholar] [CrossRef]
- Ramesh, G.; Ranjith Babu, V. Combined Facts and Microgrid-Based Congestion Management in Transmission Lines. In Advances in Electrical and Computer Technologies; Springer: Singapore, 2021; pp. 1063–1073. [Google Scholar]
- Ton, D.T.; Smith, M.A. The U.S. Department of Energy’s Microgrid Initiative. Electr. J. 2012, 25, 84–94. [Google Scholar] [CrossRef]
- Yadav, M.; Pal, N.; Saini, D.K. Microgrid Control, Storage, and Communication Strategies to Enhance Resiliency for Survival of Critical Load. IEEE Access 2020, 8, 169047–169069. [Google Scholar] [CrossRef]
- Al-Ismail, F.S. DC Microgrid Planning, Operation, and Control: A Comprehensive Review. IEEE Access 2021, 9, 36154–36172. [Google Scholar] [CrossRef]
- Sinha, S.; Bajpai, P. Power Management of Hybrid Energy Storage System in a Standalone DC Microgrid. J. Energy Storage 2020, 30, 101523. [Google Scholar] [CrossRef]
- Naderipour, A.; Saboori, H.; Mehrjerdi, H.; Jadid, S.; Abdul-Malek, Z. Sustainable and Reliable Hybrid AC/DC Microgrid Planning Considering Technology Choice of Equipment. Sustain. Energy Grids Netw. 2020, 23, 100386. [Google Scholar] [CrossRef]
- Rousis, A.O.; Konstantelos, I.; Strbac, G. A Planning Model for a Hybrid AC–DC Microgrid Using a Novel GA/AC OPF Algorithm. IEEE Trans. Power Syst. 2019, 35, 227–237. [Google Scholar] [CrossRef] [Green Version]
- Pandey, S.; Han, J.; Chen, H.; Pabst, P.M.; Gurung, N.; Li, Z.; Zhang, L.; Khodaei, A. Robust Optimization Methodology for Generation Sizing of a Microgrid. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, 25–29 July 2021. [Google Scholar]
- Khodaei, A. Provisional Microgrids. IEEE Trans. Smart Grid 2014, 6, 1107–1115. [Google Scholar] [CrossRef]
- Shahnia, F. Stability of a Sustainable Remote Area Microgrid. In Proceedings of the IEEE Region 10 Conference (TENCON), Singapore, 22–25 November 2016. [Google Scholar]
- Albaker, A.; Khodaei, A. Elevating Prosumers to Provisional Microgrids. In Proceedings of the IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar]
- Wang, Z.; Wu, X.; Li, L.; Ying, Y. Microgrid Planning Considering the Uncertainty of Renewable Generation Profile. In Proceedings of the IEEE 2nd International Electrical and Energy Conference (CIEEC), Beijing, China, 4–7 November 2018. [Google Scholar]
- Zhao, G.; Wang, D. Comprehensive Evaluation of AC/DC Hybrid Microgrid Planning Based on Analytic Hierarchy Process and Entropy Weight Method. Appl. Sci. 2019, 9, 3843. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, S.; Ullah, I.; Jamil, F.; Kim, D. Toward the Optimal Operation of Hybrid Renewable Energy Resources in Microgrids. Energies 2020, 13, 5482. [Google Scholar] [CrossRef]
- Ferdous, S.M.; Shahnia, F.; Shafiullah, G. Power Sharing and Control Strategy for Provisionally Coupled Microgrid Clusters through an Isolated Power Exchange Network. Energies 2021, 14, 7514. [Google Scholar] [CrossRef]
- Costa, L.F.; Liserre, M. Failure Analysis of the DC-DC Converter: A Comprehensive Survey of Faults and Solutions for Improving Reliability. IEEE Power Electron. Mag. 2018, 5, 42–51. [Google Scholar] [CrossRef]
- Peyghami, S.; Wang, Z.; Blaabjerg, F. A Guideline for Reliability Prediction in Power Electronic Converters. IEEE Trans. Power Electron. 2020, 35, 10958–10968. [Google Scholar] [CrossRef]
- Peyghami, S.; Blaabjerg, F. Availability Modeling in Power Converters Considering Components Aging. IEEE Trans. Energy Convers. 2020, 35, 1981–1984. [Google Scholar] [CrossRef]
- Fischer, K.; Pelka, K.; Bartschat, A.; Tegtmeier, B.; Coronado, D.; Broer, C.; Wenske, J. Reliability of Power Converters in Wind Turbines: Exploratory Analysis of Failure and Operating Data From a Worldwide Turbine Fleet. IEEE Trans. Power Electron. 2018, 34, 6332–6344. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, G.; Blaabjerg, F. Optimal Selection of Power Converter in DFIG Wind Turbine With Enhanced System-Level Reliability. IEEE Trans. Ind. Appl. 2018, 54, 3637–3644. [Google Scholar] [CrossRef] [Green Version]
- Tu, P.; Yang, S.; Wang, P. Reliability- and Cost-Based Redundancy Design for Modular Multilevel Converter. IEEE Trans. Ind. Electron. 2018, 66, 2333–2342. [Google Scholar] [CrossRef]
- Khodaei, A.; Bahramirad, S.; Shahidehpour, M. Microgrid Planning Under Uncertainty. IEEE Trans. Power Syst. 2015, 30, 2417–2425. [Google Scholar] [CrossRef]
- Khodaei, A. Provisional Microgrid Planning. IEEE Trans. Smart Grid 2017, 8, 1096–1104. [Google Scholar] [CrossRef]
- Woo, C.K.; Pupp, R.L. Costs of Service Disruptions to Electricity Consumers. Energy 1992, 17, 109–126. [Google Scholar] [CrossRef]
- Schoenung, S. Energy Storage Systems Cost Update: A Study for the DOE Energy Storage Systems Program; Sandia Report SAND; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2011. [Google Scholar]
- Microgrid Project at IIT. Available online: http://www.iitmicrogrid.net/microgrid.aspx (accessed on 10 March 2022).
- NREL. Available online: http://www.nrel.gov/analysis/tech-lcoere-cost-est.html (accessed on 10 March 2022).
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton Univ. Press: Princeton, NJ, USA, 2009. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).