Abstract
Stock market forecasting has always been researched extensively in Social Sciences. In this research, Fuzzy time series with deep learning is widely adopted to create a fuzzy convolutional neural network integration model as this model enhances the fuzzification of values to enhance feature characteristics using two-dimensional input data in convolutional neural networks (CNNs). This allows the model to retain complete feature information. The fuzzy convolutional neural network (FCNN) model autonomously learns and extracts crucial features by integrating stock market data, resulting in improved forecasting accuracy. In this study, the model was tested for forecasting the Taiwan Weighted Stock Index and metrics such as the mean squared error (MSE) and mean absolute error (MAE), and the results were compared with the real data. The results showed that the model provided accurate predictions.
1. Introduction
For stock market predictions, historical data are mainly used [1]. The Taiwan Stock Exchange index is influenced by international indices such as the Dow Jones Industrial Average, the Nasdaq Composite, and the Philadelphia Semiconductor Index, showing a positive correlation [2]. In related research, time series models, such as simple moving averages, weighted moving averages, and exponential smoothing, are commonly used [1,3]. Model forecasts are based on the difference between the predicted value for the next period and the actual value for the current period [1]. The advantages of the model are its simplicity and ease of understanding. However, the forecasts are less accurate as the data are susceptible to disturbances. In 1993, Song and Chissom introduced the fuzzy time series, which combined fuzzy theory with semantic effectiveness, using fuzzy relationships for reasoning and forecasting [4,5,6]. In 1996, Chen utilized a first-order fuzzy time series model to forecast publicly available data on new student admissions at the University of Alabama [5,6]. The results indicated that the first-order fuzzy time series model was relatively simple and less affected by disturbed data. However, due to its simplicity, it is unable to explain complex relationships.
Many scholars have improved these models [7,8,9,10,11,12]. In fuzzy time series, the interval length relies on the researcher’s experience or expert judgment. Cheng et al. [11] introduced fuzzy cluster time series to partition the domain and address the issue of determining equal interval lengths to set the universe and interval lengths. Bose and Mali [13] reviewed fuzzy time series and determined the domain space, partitioned the domain, and fuzzified past data by using common steps in fuzzy time series and establishing fuzzy relationships through defuzzification (which is optional). High-dimensional fuzzy relationship calculations are complex, and researchers adjust weights to correct errors. However, this process relies on manual or expert judgment [9,10,11,12].
Deep learning has been widely used in recent years [9,10,14,15]. Aladag et al. used neural networks for fuzzy time series forecasting in 2009 and 2010 [9,10]. Tran et al. applied neural networks to handle multiple indicators for predicting resource utilization [15]. Neural networks, compared with traditional regression models, demonstrate enhanced fault tolerance [3,16,17]. The characteristics of neural networks in deep learning make them well suited to time series forecasting. However, in most time series applications, the computational process often focuses on adjustments by moving windows, periods, neurons, and layers, while neglecting the numerical features. Therefore, CNNs are used to analyze data using two-dimensional image information, which preserves the intrinsic features of the data. This capability was used in this research to integrate two-dimensional image information with fuzzy logic in the deep learning network architecture. Then, more information was obtained, making the model more accurate than traditional models.
In this research, we proposed an integrated model by combining fuzzy time series with deep learning. In the developed model, information features are well preserved, and the numerical calculations align with human cognitive patterns. The proposed FCNN forecasting model avoids relying on expert judgment and simplifies the complex calculations of traditional fuzzy time series models. These adjustments are applied to stock price forecasting to reduce and correct prediction errors to enhance the accuracy of predictions. The proposed model was validated through stock price forecasting for the Taiwan stock market, demonstrating enhanced accuracy compared to existing methods.
2. Materials and Methods
2.1. Deep Learning
Deep neural networks (DNNs) are capable of learning more complex patterns and achieving better performance [14]. Deep learning has been used widely with impressive results [9,10,14,15,16]. CNNs are feedforward neural networks that simulate human neural transmission. In CNN, information is input into a neuron and then received from the output of the previous neuron, constructing a multilayer perceptron model [18]. This model is a popular deep learning model, allowing automatic feature extraction and compression in model training [15,16,17,18].
2.2. Principles and Concepts of Fuzzy Logic
Fuzzy set theory was introduced by Professor Zadeh at the University of California, Berkeley, in 1965 [19]. It refers to the degree to which an element belongs to a set. If an element fully belongs to the set, its membership value is 1; if it does not belong at all, its value is 0. For partial membership, the value is between 0 and 1, representing the degree of membership [19]. Fundamentally, fuzzy sets are regarded as an extension of traditional sets. The fuzzy set theory allows for the quantification of human subjective thinking and judgment processes using fuzzy sets. It is applied to address uncertainty and ambiguity as it emphasizes human thinking, reasoning, and perception of the surrounding world.
2.3. Fuzzy Time Series
Since Song and Chissom [4,5,6] introduced fuzzy time series, many researchers have used them. The first-order fuzzy time series model is mainly used. In the model, the data from the previous period are used as a calculation factor. In contrast, higher-order fuzzy time series models consider the effects of different periods.
2.4. Evaluation
In prediction, accuracy and unbiased forecasts must be ensured. Various prediction errors have been proposed, such as the commonly used mean square error (MSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and root mean squared error (RMSE) [1].
3. Results
We used the two-dimensional images to construct a new FCNN model to improve the problem of determining weight parameters in previous fuzzy time series models. By utilizing the concept of 2D images in CNNs, feature information was retained more comprehensively. By combining fuzzy theory with CNNs, the numerical computations became more rational and aligned with human thinking patterns. Incorporating difference and fuzzy computations enhances feature information and reduces the margin of error. The developed FCNN model automated the calculations, whereas traditional fuzzy time series models, such as the adaptive expectation model, rely on manual or expert settings for parameter weight adjustments [11,20]. For the comparison of prediction accuracy and the validation of the model, we used Taiwan stock prices. The research framework is illustrated in Figure 1.
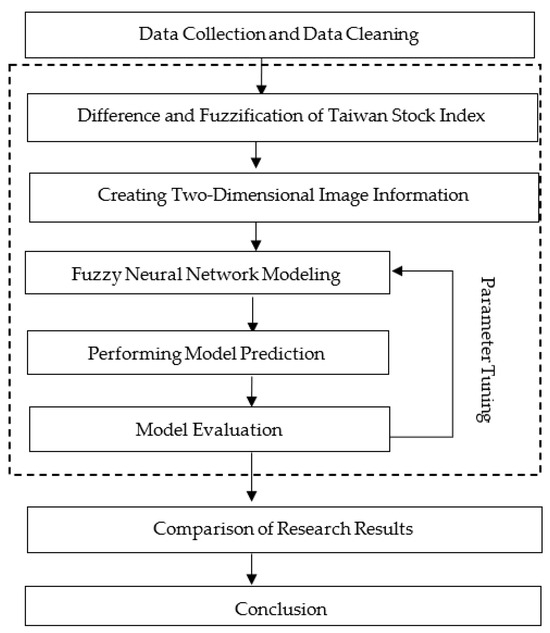
Figure 1.
Research framework.
FCNN Model
We cleaned data collected from the Taiwan Weighted Stock Index as well as relevant international indices, including the Dow Jones Industrial Average (DJI), Nasdaq Composite Index (NASDAQ), and Philadelphia Semiconductor Index (SOX). The first-order difference between the current and previous period’s actual value was calculated to obtain stock market data and perform fuzzification. We employed fuzzification methods [4,5,6,7] as they are straightforward and simplify complex computations. Using feature attributes and periods to construct two-dimensional information, feature data served as input values for the neural network. The evaluation metrics RMSE, MSE, MAE, and MAPE were calculated [1] to compare the results of the FCNN model on the CNN deep learning network with traditional methods without fuzzification.
4. Discussion
The Taiwan Weighted Stock Index was used to verify the forecasting performance of the proposed method. International indices such as the Dow Jones Industrial Average, Nasdaq Composite Index, and Philadelphia Semiconductor Index from 2018 were also used for data collection and cleaning. In data cleaning, the following non-trading days were removed due to the differing trading dates between Taiwan and U.S. markets: U.S. stock market dates (13–20 February 2018, 28 February 2018, 4–6 April 2018, 1 May 2018, 18 June 2018, 24 September 2018, 10 October 2018) and Taiwan stock market dates (15 January 2018, 30 March 2018, 30 May 2018, 4 July 2018, 3 September 2018, 22 November 2018, 5 December 2018). A total of 245 data points were selected for the experiment. The YFinance package was used for data scraping. In this study, the experimental data indicators were classified into four groups with parameter settings of batch_size = 20, validation_split = 0.2 (Table 1).

Table 1.
Experimental feature indicators.
First, the feature dataset was created by establishing two-dimensional graphical information for input. Figure 2 shows the first four training data points. The data were presented on a heatmap, with the interval ranging from 0 to 1. Darker colors represent smaller values, while lighter colors represent larger values. “Periods” refers to using the feature data from the previous five periods to predict the target value for the 6th period.
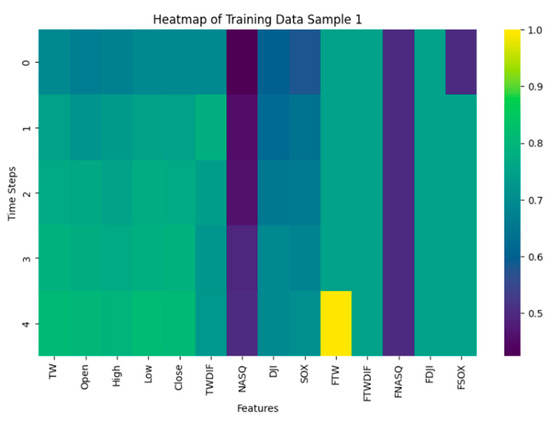
Figure 2.
Visualization of two-dimensional feature data information.
In the FCNN model, the dropout was set to 0.2 and the pool size to 2. Table 2 shows the training data while Table 3 shows the test data. Experimental groups 2 and 4 included fuzzified features and demonstrated better performance. Adding fuzzified features enhanced feature learning. Specifically, the MAE for the training dataset was 148.09 for experiment 1 and 71.91 for experiment 2, while the MAE for the test dataset was 644.63 and 612.10, respectively.

Table 2.
Comparison of training results between experimental groups 1 and 2.

Table 3.
Comparison of testing results between experimental groups 1 and 2.
In the research, we added features to common indicators such as the opening price, daily high price, daily low price, and closing price to observe changes in the experimental results. The training results of experimental groups 3 and 4 were similar, with an improvement in the test data. Through fuzzification, the network results of CNNs were enhanced, which necessitates further research on indicators.
5. Conclusions
We developed an integrated model by combining fuzzy time series with deep learning. By integrating two-dimensional image information with fuzzy concepts, the model retained complete information features and provided calculations more closely with human thinking patterns. By combining CNNs, issues associated with traditional weight dependency on expert judgments were avoided, and the complex fuzzy relationship of traditional fuzzy time series was simplified. The model adjusted the value predictions to reduce errors by incorporating interpolation and fuzzification features. By leveraging fuzzification-enhanced features, the method enhanced accuracy significantly.
Author Contributions
Conceptualization, J.-W.W. and J.-S.C.; methodology, J.-W.W.; formal analysis, J.-W.W. and J.-S.C.; writing—original draft preparation, J.-W.W.; writing—review and editing, J.-W.W. and J.-S.C.; supervision, J.-S.C.; funding acquisition, J.-W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by Chaoyang University of Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The stock market data used in this study are publicly available from various financial data platforms.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wisner, J.D.; Leong, G.D.; Tan, K.C. Principles of Supply Chain Management—A Balanced Approach; South-Western Cengage Learning: Boston, MA, USA, 2005. [Google Scholar]
- Wang, K.L.; Chen, M.L. The Dynamic Linkages of U.S. and Taiwan Stock Market Indices in the Pre- and Post-Asian Financial Crises Periods. Taiwan Econ. Rev. 2003, 31, 191–252. [Google Scholar]
- Gençay, R. Non-linear prediction of security returns with moving average rules. J. Forecast. 1996, 15, 165–174. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Fuzzy time series and its models. Fuzzy Sets Syst. 1993, 54, 269–277. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Forecasting enrollments with fuzzy time series—Part I. Fuzzy Sets Syst. 1993, 54, 1–9. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Forecasting enrollments with fuzzy time series—Part II. Fuzzy Sets Syst. 1994, 62, 1–8. [Google Scholar] [CrossRef]
- Chen, S.-M. Forecasting enrollments based on fuzzy time series. Fuzzy Sets Syst. 1996, 81, 311–319. [Google Scholar] [CrossRef]
- Chen, S.-M. Forecasting enrollments based on high-order fuzzy time series. Cybern. Syst. Int. J. 2002, 33, 1–16. [Google Scholar] [CrossRef]
- Aladag, C.H.; Basaran, M.A.; Egrioglu, E.; Yolcu, U.; Uslu, V.R. Forecasting in high order fuzzy times series by using neural networks to define fuzzy relations. Expert Syst. Appl. 2009, 36, 4228–4231. [Google Scholar] [CrossRef]
- Aladag, C.H.; Yolcu, U.; Egrioglu, E. A high order fuzzy time series forecasting model based on adaptive expectation and artificial neural networks. Math. Comput. Simul. 2010, 81, 875–882. [Google Scholar] [CrossRef]
- Cheng, C.H.; Cheng, G.W.; Wang, J.W. Multi-attribute fuzzy time series method based on fuzzy clustering. Expert Syst. Appl. 2007, 34, 1235–1242. [Google Scholar] [CrossRef]
- Cheng, C.H.; Chen, T.L.; Teoh, H.J.; Chiang, C.H. Fuzzy time-series based on adaptive expectation model for TAIEX forecasting. Expert Syst. Appl. 2008, 34, 1126–1132. [Google Scholar] [CrossRef]
- Bose, M.; Mali, K. Designing fuzzy time series forecasting models: A survey. Int. J. Approx. Reason. 2019, 111, 78–99. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Gated feedback recurrent neural networks. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6 July 2015; pp. 2067–2075. [Google Scholar]
- Tran, N.; Nguyen, T.; Nguyen, B.M.; Nguyen, G. A Multivariate Fuzzy Time Series Resource Forecast Model for Clouds using LSTM and Data Correlation Analysis. Procedia Comput. Sci. 2018, 126, 636–645. [Google Scholar]
- Kocak, C.; Egrioglu, E.; Bas, E. A new deep intuitionistic fuzzy time series forecasting method based on long short-term memory. J. Supercomput. 2021, 77, 6178–6196. [Google Scholar] [CrossRef]
- Kimoto, T.; Asakawa, K.; Yoda, M.; Takeoka, M. Stock market prediction system with modular neural networks. In Proceedings of the 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; p. 137535. [Google Scholar]
- Lin, T.K.; Lin, Y.T.; Kuo, K.W. Application of Convolution Neural Network and Neural Network Entropy Algorithm for Structural Health Monitoring. Struct. Eng. 2022, 37, 64–85. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Chen, T.L.; Cheng, C.H.; Teoh, H.J. Fuzzy time-series based on Fibonacci sequence for stock price forecasting. Phys. A 2007, 380, 377–390. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).