A Novel Approach for Classifying Gliomas from Magnetic Resonance Images Using Image Decomposition and Texture Analysis ^†

Abstract

Accurate glioma categorization using magnetic resonance (MR) imaging is critical for optimal treatment planning. However, the uneven and diffuse nature of glioma borders makes manual classification difficult and time-consuming. To address these limitations, we provide a unique strategy that combines image decomposition and local texture feature extraction to improve classification precision. The procedure starts with a Gaussian filter (GF) to smooth and reduce noise in MR images, followed by non-subsampled Laplacian Pyramid (NSLP) decomposition to capture multi-scale image information, making glioma borders more visible, TV-L1 normalization to handle intensity discrepancies, and local binary patterns (LBPs) to extract significant texture features from the processed images, which are then fed into a range of supervised machine learning classifiers, such as support vector machines (SVMs), K-nearest neighbors (KNNs), decision trees (DTs), AdaBoost, and LogitBoost, which have been trained to distinguish between low-grade (LG) and high-grade (HG) gliomas. According to experimental findings, our proposed approach consistently performs better than the state-of-the-art glioma classification techniques, with a higher degree of accuracy in differentiating LG and HG gliomas. This method has the potential to significantly increase diagnostic precision, enabling doctors to make better-informed and efficient treatment choices.

1. Introduction

The most common primary brain tumors in adults are gliomas, which originate from glial cells and mainly impact the central nervous system (CNS) [1]. They typically occur between the ages of 45 and 65 and are more prevalent in men (7.14 per 100,000) than in women (5.06 per 100,000) [2]. Glioma formation is significantly influenced by genetic variations, such as changes in Isocitrate Dehydrogenase 1 and 2 (IDH1 and IDH2), as well as environmental variables, such as smoking, drinking, and electromagnetic radiation exposure [3]. Depending on where the tumor is located, symptoms could include headaches, seizures, memory loss, personality changes, and trouble speaking.

Gliomas are classified according to their location (supratentorial, infratentorial, or pontine), morphology (astrocytoma, oligodendroglioma, or ependymoma) [4], and World Health Organization (WHO) grades (I–IV) [5]. While grades III and IV are categorized as high-grade (HG), grades I and II are categorized as low-grade (LG). Among other imaging techniques, magnetic resonance imaging (MRI) has better contrast and sensitivity; therefore, it is widely used in glioma investigation. However, due to their uneven borders and fluctuating pixel intensities, gliomas are difficult to detect in MRI scans. Hence, to improve diagnostic precision, this study suggests a novel method for precisely predicting whether a glioma is LG or HG.

The structure of this study is outlined as follows: Section 2 explores existing methods for brain tumor detection. Section 3 introduces the proposed approach for predicting gliomas. Section 4 compares the experimental results of the proposed and existing techniques, along with an analysis of the critical factors driving the success of the proposed method. Finally, Section 5 concludes by summarizing the findings and effectiveness of the suggested approach.

2. Related Works

This section explores several recently developed MRI-based approaches for the detection of gliomas, highlighting their methodologies and summarizing the limitations of existing techniques.

Sharif et al. [6] proposed an unsupervised learning technique integrated with extreme learning (ELM) methods for identifying glioma brain tumors. Via this approach, the authors achieved a sensitivity of 95%, a specificity of 93%, and an overall accuracy of 96.5%. To improve brain tumor classification performance, Amin et al. [7] implemented a methodology integrating discrete wavelet transform (DWT) with convolutional neural networks (CNNs), obtaining 98% sensitivity, 92% specificity, and 96% accuracy. Chandra et al. [8] developed a computer-aided detection (CAD) system for automatic tumor segmentation and classification using fractional mesh-free partial differential equations (FMFPDEs) and support vector machines (SVMs). Through this system, they attained an accuracy of 97.5%, a sensitivity of 97.5%, and a specificity of 96.08%.

Reddy and Ravindra Dhuli [9] developed a system that used an adaptive mechanism, entropy-based local directional patterns (ELDPs), and linear SVM, yielding an accuracy of 94.44%, sensitivity of 89.17%, and specificity of 97.08%. Aamir Hafeez et al. [10] introduced a customized CNN framework for assessing gliomas using MRI images. Based on these sequences of operations, the authors attained 97.85% accuracy, 99.88% sensitivity, and 98.88% specificity. Jainy Sachdeva et al. [11] presented a hybrid model combining residual and efficient nets to classify gliomas into LG and HG. Through this framework, they yielded 97.59% accuracy and 98% sensitivity. Rachmawanto et al. [12] employed a simple CNN architecture for glioma tumor prognosis using MRI images, achieving 94.14% accuracy, 95.84% sensitivity, and 90.08% specificity.

2.1. Research Gaps

From the above-mentioned literature review observed the following issues:

• Many methods (ELM by Sharif et al. [6], CNN by Hafeez et al. [10]) do not explicitly address noise and contrast variations in MRI images. This can affect tumor boundary visibility;
• Some models, such as DWT-CNN by Amin et al. [7] and FMFPDE-SVM by Chandra et al. [8], focus on feature extraction but may not fully capture multi-scale texture and boundary information;
• Traditional CNN models (e.g., by Rachmawanto et al. [12]) rely on feature maps but may struggle with accurate segmentation of glioma regions;
• Methods such as ELDP-SVM by Reddy and Dhuli [9] use entropy-based patterns but may miss finer details in tumor texture;
• CNN-based approaches (e.g., those by Hafeez et al. [10] and Sachdeva et al. [11]) require large datasets for training and may overfit small datasets.

After analyzing the aforementioned methods, we have developed a novel approach that integrates Gaussian filtering (GF), the non-subsampled Laplacian pyramid (NSLP), principle component analysis (PCA), total variation-L1 (TV-L1) normalization, local binary pattern (LBP), and supervised learning techniques.

2.2. Key Contributions

The major contributions of our proposed methodology are summarized as follows:

• With the help of GF, we significantly smoothen brain MRI images by eliminating unnecessary details that could affect classification. Further, to improve the visibility of glioma boundaries, we employed NSLP, since it preserves important high-frequency details. This allows us to differentiate LG and HG tumors relatively well;
• TV-L1 separates essential tumor structures (cartoon component) from noise and minor texture variations, aiding in robust feature extraction. Further, we passed LBP through the texture component of TV-L1 decomposition to capture local patterns and edge information that improve the feature representation for machine learning classifiers. Due to this strategic combination, the proposed model attained better performance compared with the existing models

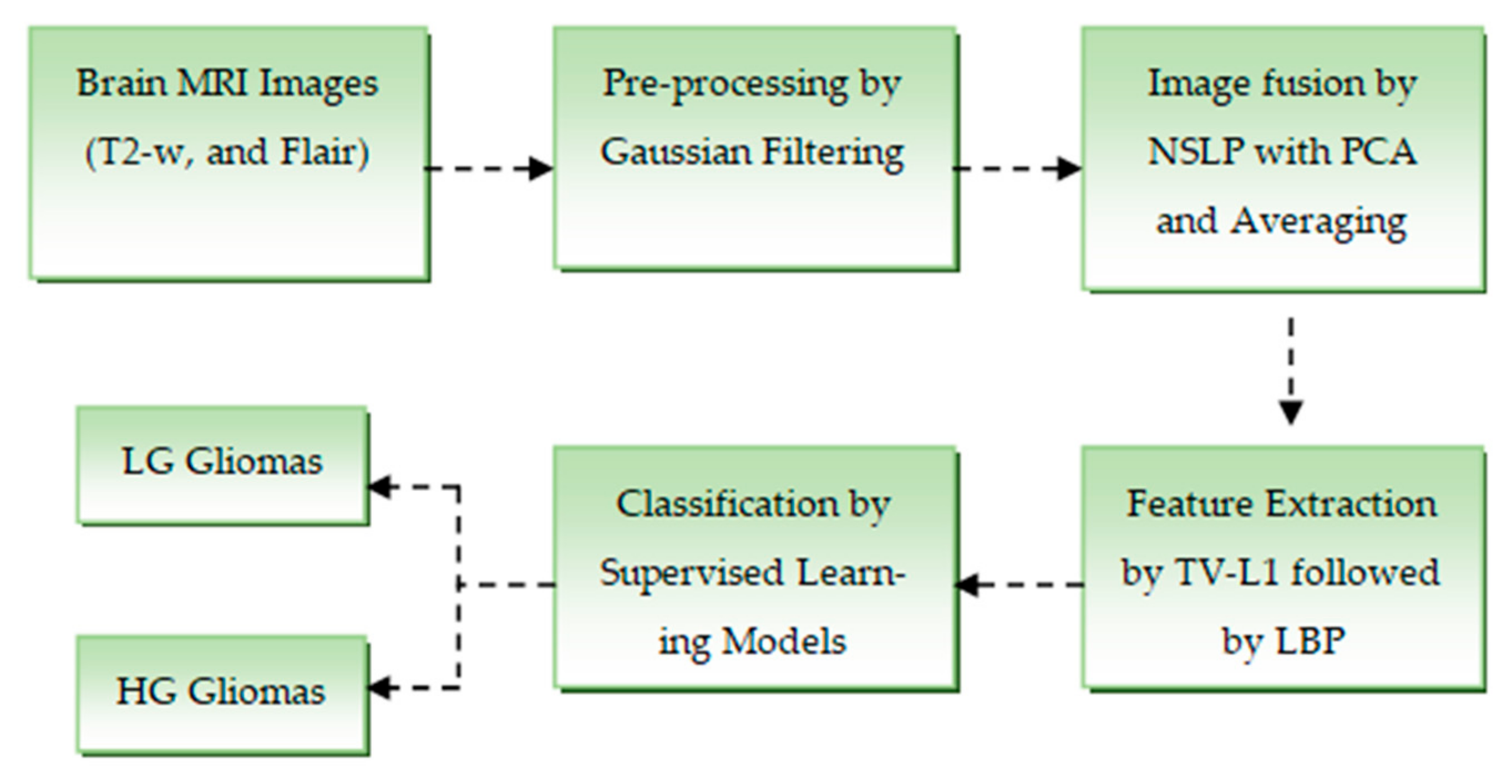
3. Materials and Methods

This section describes the step-by-step implementation of the proposed methodology. Figure 1 illustrates the overall block diagram of the model, which comprises four main stages: pre-processing, image fusion, texture feature extraction, and classification.

3.1. Materials

In this work, we utilized the BraTS 2015 dataset [13] to analyze the performance of the suggested model. This database includes 110 testing cases with both LG and HG gliomas and 274 training instances with 220 HG and 54 LG gliomas. Each testing case includes four MRI sequences: T1, T1C, T2, and FLAIR. To evaluate the efficiency of the presented approach, we mainly focus on the T2 and FLAIR sequences.

3.2. Pre-Processing

Noise remains a significant challenge in the acquisition of brain MRI tumor images. This issue can be effectively addressed using simple image enhancement techniques, which minimize noise while improving the contrast and brightness of images. Over the past few decades, numerous image denoising methods have been developed to enhance image quality [14]. Among these, Gaussian filtering (GF) [15] is one of the most widely used techniques for reducing noise and improving the quality of brain MRI tumor images. Gaussian filtering effectively smoothens an image, preparing it for subsequent processing. Following this, image fusion is applied to further enhance diagnostic performance.

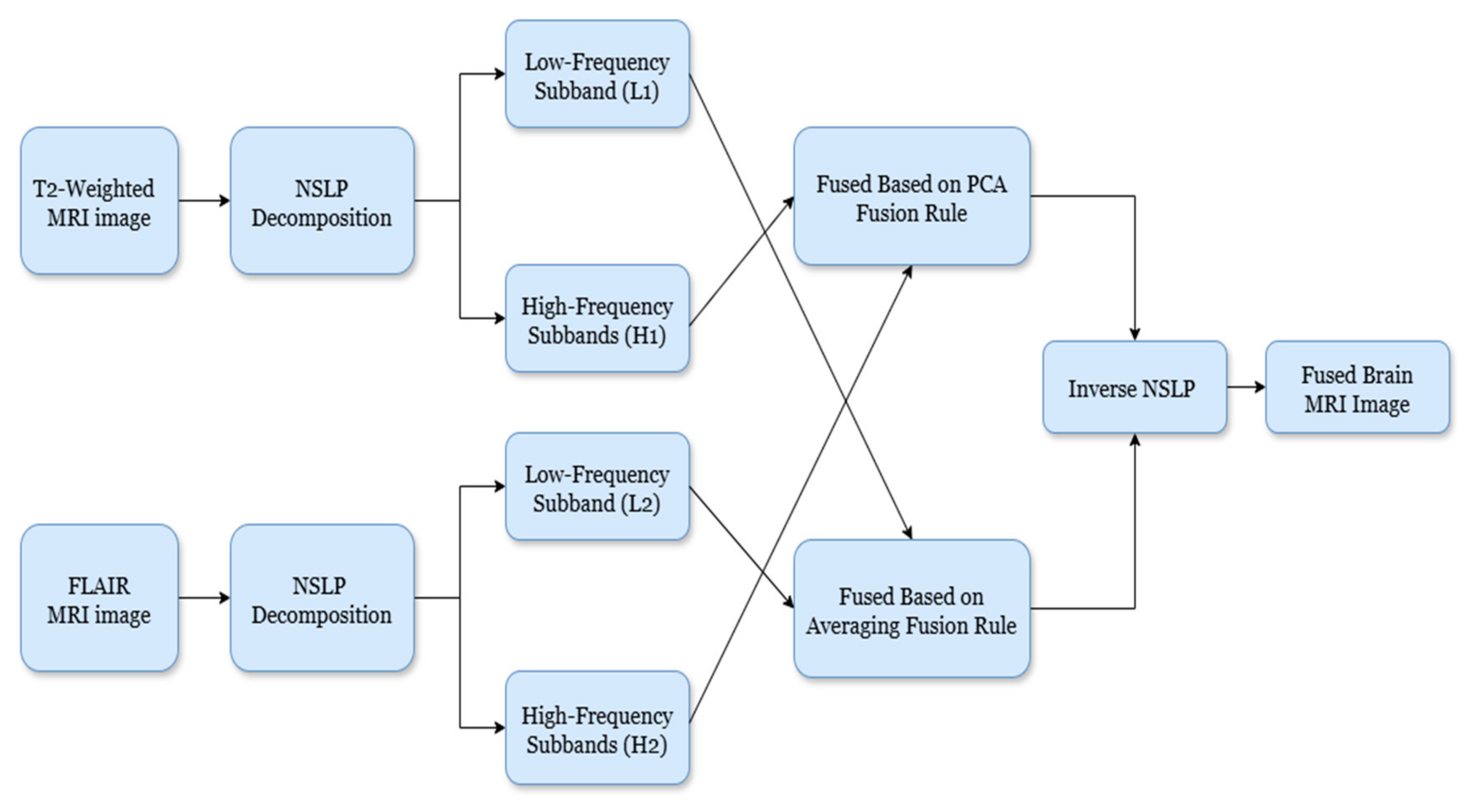
3.3. Brain MRI Image Fusion

The primary objective of image fusion is to improve the model’s ability to detect glioma brain tumors by accentuating abnormalities. This is achieved by merging T2-weighted and FLAIR MRI imaging sequences from the same patient. The fusion process utilizes non-subsampled Laplacian pyramid (NSLP) decomposition combined with principal component analysis (PCA) and averaging fusion. Figure 2 illustrates the proposed methodology for fusing brain MRI images. The step-by-step process of the proposed fusion as follows:

• Image Decomposition: To achieve image decomposition, in this work, we introduced the NSLP-based decomposition approach [16]. NSLP is a multi-resolution analysis strategy that subdivides images into a set of subbands (low-frequency and high-frequency) at different scales and orientations. In this work, we introduced a two-stage NSLP decomposition to decompose the enhanced brain MRI gliomas, resulting in three subbands: one low-frequency (LF) and two high-frequency (HF) subbands. Here, LF subbands illustrate coarse structures, whereas HF subbands illustrate fine details and edges. Further, to improve detection accuracy, these subbands are concatenated using image fusion techniques. To fuse the HF subbands, we utilized principal component analysis (PCA), while for LF subbands, the averaging rule is considered as the fusion rule. Via this process, we can preserve the relevant image details and enhance the overall accuracy of the model;
• High-Frequency Fusion: The HF subbands of both brain MRI glioma images are concatenated using a PCA-based fusion rule, as introduced by Vijayarajan et al. [17]. Here, PCA recognizes the most meaningful principal components within the image. Therefore, by employing PCA on the HF subbands, we can select and combine the components that capture the most significant details from both modalities, resulting in the HF fused subband;
• Low-Frequency Fusion: Here, the LF subbands from both brain tumor images (T1-weighted and FLAIR) are merged using a simple approach, namely averaging [17]. The pixel values of corresponding LF subbands of both images are averaged to attain the fused LF subband;
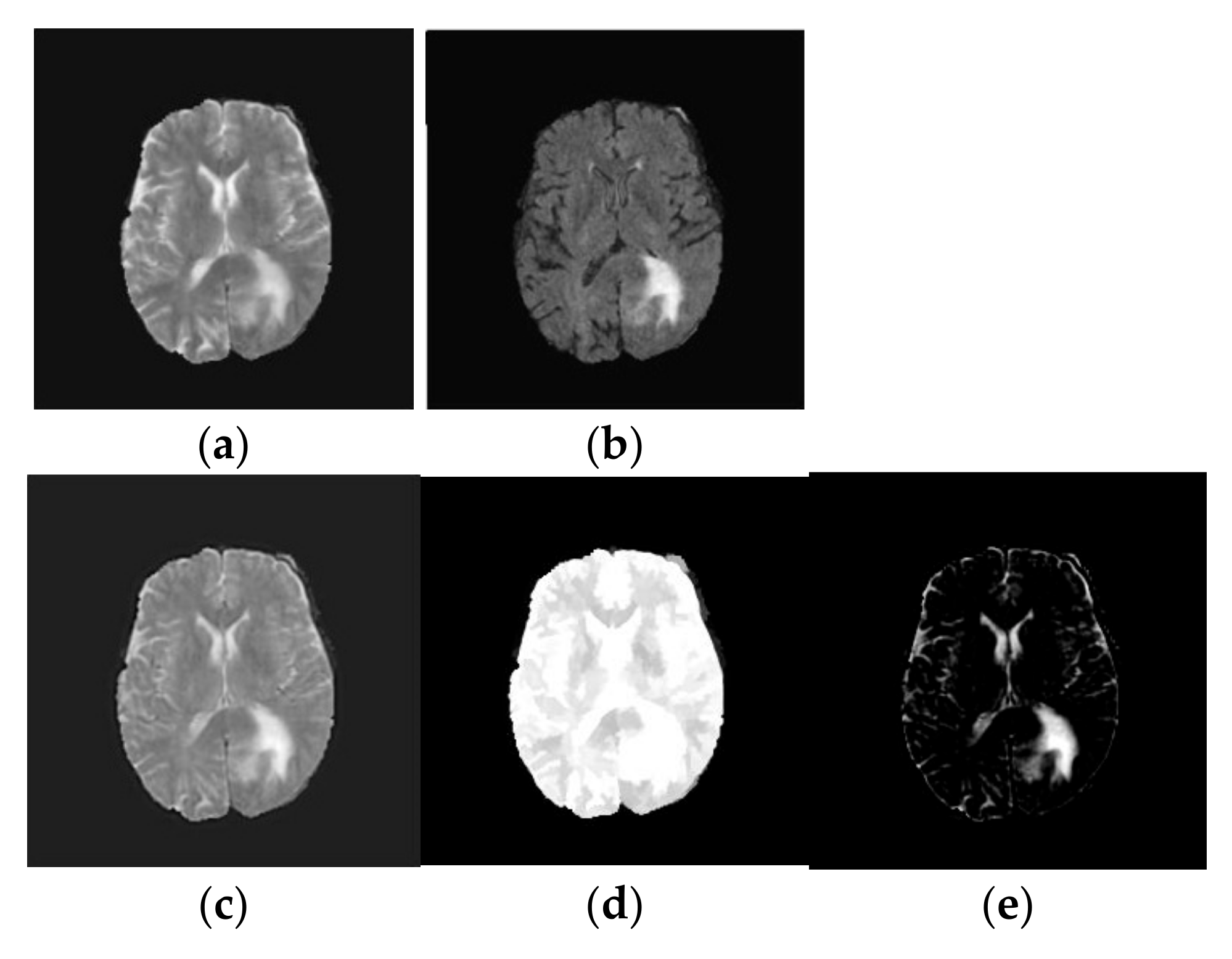
• Image Reconstruction: Finally, the fused low-frequency and high-frequency subbands are recombined using the inverse NSLP. This process reconstructs the final fused MRI image, which is expected to contain the complementary information from both T1-weighted and FLAIR images. The implications of the fused process are shown in Figure 3.

3.4. Feature Extraction

Features play a crucial role in solving classification problems, with texture features being particularly significant as they provide valuable information about the intensity and spatial structure of an image. Building on this concept, this study introduces a novel approach that combines total-variation L1 (TV-L1)-based cartoon-texture decomposition with local binary pattern (LBP) analysis to extract meaningful features from fused brain MRI images. This method ensures the extraction of relevant and discriminative features, enhancing the classification performance. The step-by-step process of the proposed feature extraction model as follows:

• TV-L1 Decomposition: The primary objective of our method is to decompose the fused image, $F(x,y)$ into two distinct components: a piecewise smooth (geometric) component and a texture component. The geometric component represents the smooth regions and boundaries of the image, while the texture component captures oscillating features, including edges and noise. In medical imaging, the texture component often contains critical structural details that are essential for tasks such as tumor classification. These structural details can be effectively extracted using the TV-L1-based cartoon-texture decomposition technique. The TV-L1 method separates the fused brain MRI tumor image into two components: the cartoon (geometric) component and the texture component, as outlined in [18]:

  $$F(x,y)=S+T$$

  (1)

  where $S$ gives the cartoon part and which characterizes the geometric component of the fused image. Similarly, $T$ represents the texture part of the fused image. The cartoon component of the fused image is attained by minimizing the following objective function [18]:

  $${\min }_S{\displaystyle {\int }_{\Omega }\left|\nabla S\right|}+\lambda {‖F-S‖}_{1}d\Omega$$

  (2)

  where $\nabla$ represents the gradient operator and λ defines the regularization criteria which is a trade-off between the fidelity criteria and regularization term. In this work, we chose λ as 0.1. Similarly, $\Omega \subset Z^2$ denotes the image domain and the symbol ${‖.‖}_1$ represents L¹ normalization. The first part of Equation (2) represents the TV of cartoon component and the second part specifies the fidelity to make the cartoon part $S$ keep close to the fused image, and they are calculated over the image domain Ω. The solution to Equation (2) is resolved by the following optimization [19]:

  $$S_{x,y}^{l+1}=S_{x,y}^l+{\displaystyle \frac{D_t}{D_p{D}_q}}\left({\nabla }_p^{-}\left({\displaystyle \frac{{\nabla }_p^{+}{S}_{x,y}^l}{\left|\nabla S_{x,y}^l\right|+\phi }}\right)+{\nabla }_q^{-}\left({\displaystyle \frac{{\nabla }_q^{+}{S}_{x,y}^l}{\left|\nabla S_{x,y}^l\right|+\phi }}\right)\right) +D_t\left(\lambda {\displaystyle \frac{F_{x,y}-S_{x,y}^l}{{\left(F_{x,y}-S_{x,y}^l\right)}^2+\epsilon }}\right)$$

  (3)

  where ${\nabla }^{-}$ and ${\nabla }^{+}$ represent the forward and backward differences. $\left|\nabla S_{x,y}\right|$ provides the magnitude of gradient. The parameter l provides the iteration index. In this, we chose l as 50. $D_t$ is defined as changes in time, and $D_p$ and $D_q$ indicate discrete spatial distances of the image grid. φ and ε (0.00001) are constants. The resultant outcome of TV-L1 decomposition is shown in Figure 3.
• Local binary patterns (LBPs): To further enhance classification performance, local features were extracted from the texture component of the fused image ($T$) using the LBP technique [20]. LBP is a simple yet powerful texture descriptor that labels the pixels of an image by thresholding the neighborhood of each pixel and converting the result into a binary number. It captures local texture patterns by comparing the intensity of each pixel with its surrounding neighbors, creating a binary code that represents the texture. The key advantage of LBP lies in its ability to capture distinct local texture patterns while establishing spatial relationships between them. Additionally, its robustness to variations in illumination and high computational efficiency make it an excellent choice for tasks such as brain tumor classification. In this work, we consider radius (R) as one, the number of neighboring pixels for thresholding as eight, and a variant of uniform LBP.
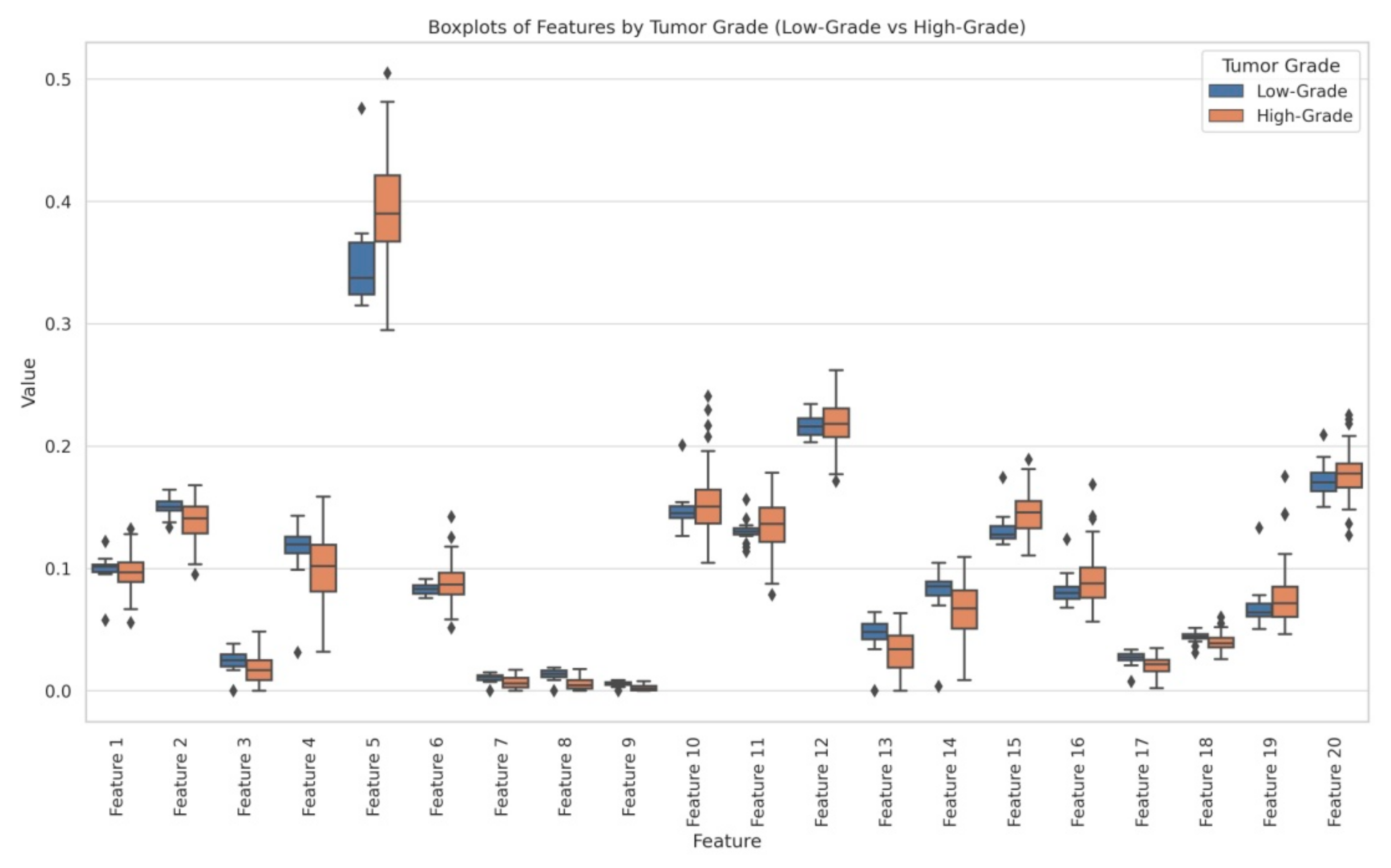
• Statistical analysis: By the above-mentioned feature engineering process, we obtained 20 radiomic features and they were analyzed through independent t-tests and ANOVA to identify significant differences between LG and HG. The statistical analysis revealed that several features exhibited significant differences between LG and HG:
  • Feature 2 (t-test p = 0.000052, ANOVA p = 0.0044);
  • Feature 5 (t-test p = 0.000742, ANOVA p = 0.00026);
  • Feature 7 (t-test p = 0.001887, ANOVA p = 0.00387);
  • Feature 8 (t-test p = 0.000005, ANOVA p = 3.73 × 10⁻⁹);
  • Feature 9 (t-test p = 0.000006, ANOVA p = 3.04 × 10⁻⁹).

For a better understanding, we generated a box plot to visualize the distribution of each feature between LG and HG, confirming clear distinctions in their values. Figure 4 represents the box plots of LG and HG features.

3.5. Classification

Features extracted from the TV-L1 followed by the LBP technique were fed to various supervised ML techniques, including SVM [21], K-nearest neighbors (KNNs) [22], decision trees (DTs) [23], AdaBoost [24], and LogitBoost [25].

Table 1. Hyperparameters of classifiers used in the suggested model.

Classifier	Key Hyperparameters
SVM	Kernel Function: ‘rbf’, and Kernel Scale: ‘auto’
KNN	Num Neighbors: 5, and Distance: ‘euclidean’
DT	Max Num Splits: 10, Split Criterion: ‘gdi’, and Prune: ‘on’
AdaBoost	Num Learning Cycles: 100, and Learn Rate: 0.1
LogitBoost	Num Learning Cycles: 100, Learn Rate: 0.1, and Max Num Splits: 10

represents the hyper parameters of the above-mentioned classifiers used in the implementation of the proposed model. Further, the performance of these approaches is assessed through various metrics such as sensitivity, specificity, precision, area under the curve (AUC), F1-score, and accuracy.

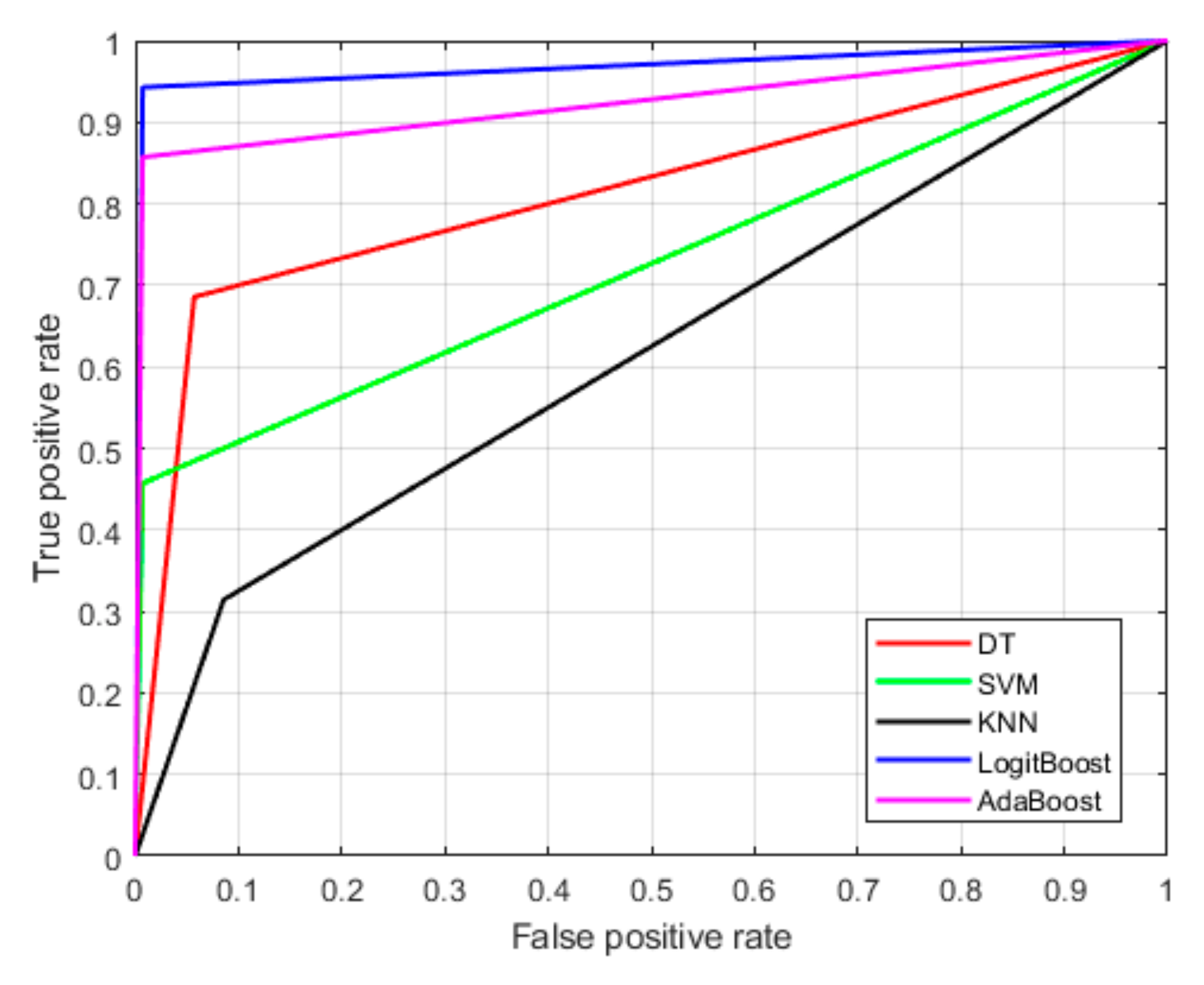
4. Results and Discussion

In this section, we discuss the simulation results of the presented approach and its comparison with the state-of-the-art methods. In addition, we summarize why our proposed method produces better outcomes compared with others.

To distinguish LG and HG gliomas, at first, we enhanced the contrast of input brain MRI images using a GF operation. Later, we employed the NSLP decomposition-based followed by PCA and averaging fusion frameworks to enhance the detection capabilities of the proposed model. Then, we extracted significant features from the fused images using the TV-L1 cartoon–texture decomposition approach. Further, we employed the LBP to retain significant structural features. Finally, the extracted features were fed into supervised learning algorithms as mentioned in Section 3.5, which effectively classify glioma brain tumors into LG and HG categories. All these experiments were conducted by dividing the dataset into 80% for training and 20% for testing.

Table 2. Classification performance of the various ML models.

Classifier	Performance Metrics (%)
	Sensitivity	Specificity	Precision	F1-Score	AUC	Accuracy
SVM	45.71	99.28	94.12	61.53	72.5	88.57
KNN	68.57	94.28	75	71.64	81.43	89.14
DT	31.42	91.43	47.82	37.92	61.43	79.43
AdaBoost	85.71	99.28	96.77	90.9	92.5	96.57
LogitBoost	94.28	99.29	97.05	95.64	96.8	98.29

provides a comparative analysis of the performance metrics for several classifiers, as we described in Section 3.5. Among these, LogitBoost stands out with exceptional results across nearly all metrics. It achieved a sensitivity of 94.28%, a specificity of 99.29%, a precision of 97.05%, an F1-Score of 95.64%, an AUC of 96.8%, and the highest accuracy of 98.29%. AdaBoost also performed impressively, with a sensitivity of 85.71%, a specificity of 99.28%, and an accuracy of 96.57%.

In contrast, the decision tree (DT) classifier exhibited the weakest performance, with the lowest sensitivity of 31.42% and precision of 47.82%, resulting in a reduced overall accuracy of 79.43%. The KNN and SVM classifiers demonstrated moderate performance. KNN achieved a sensitivity of 68.57% and an accuracy of 89.14%, while SVM had a sensitivity of 45.71% and an accuracy of 88.57%. Overall, Table 2 clearly indicates that LogitBoost is the most effective classifier among the five, excelling in most of the evaluated metrics.

Figure 5 illustrates the receiver operating characteristic (ROC) curves for various machine learning models, evaluating their classification performance. The x-axis represents the false positive rate (FPR), which measures the proportion of LG tumors incorrectly classified as HG. The y-axis represents the true positive rate (TPR), which indicates the proportion of HG tumors correctly identified by the model. An optimal classifier would have an ROC curve that closely follows the top-left corner, reflecting a high TPR and a low FPR. From the figure, LogitBoost demonstrates the best performance compared with the other models. This indicates that the LogitBoost algorithm is highly effective at correctly identifying malignant brain tumors while minimizing the likelihood of misclassifying benign tumors.

Comparison with the Existing Approaches

Table 3. Comparative analysis of the proposed and existing brain tumor classification approaches.

Method	Evaluation Criteria	Performance Measures
		Sensitivity	Specificity	Accuracy
ELM [6]	80% training and 20% testing	95	93	96.5
DWT-CNN [7]	80% training and 20% testing	98	92	96
FMFPDE-SVM [8]	5- fold cross validation	97.5	96.08	97.5
ELDP-SVM [9]	10-fold cross validation	89.19	97.08	94.44
CNN [10]	-	99.88	98.88	97.85
Hybrid Model [11]	80% training and 20% testing	98	-	97.59
Customized CNN [12]	80% training and 20% testing	95.84	90.08	94.14
The Proposed		94.28	99.29	98.25

Note: ‘-‘ indicates that the metric is not defined in the source work.

presents a comparison of various methods based on their performance metrics. From this, we observed that the ELM achieved a sensitivity of 95%, specificity of 93%, and an accuracy of 96.5%. The DWT-CNN method had a slightly higher sensitivity of 98% but a lower specificity of 92%, resulting in an overall accuracy of 96%. The FMFPDE-SVM method performed well, with a sensitivity of 97.5%, specificity of 96.08%, and an accuracy of 97.5%. The ELDP-SVM model demonstrated relatively lower sensitivity (89.19%) and specificity (90.78%), leading to an accuracy of 94.44%. A standard CNN achieved outstanding sensitivity (99.88%) and specificity (98.88%), with an accuracy of 97.82%. The hybrid model attained a sensitivity of 98% and an accuracy of 97.85%, though its specificity is not reported. The customized CNN model showed a sensitivity of 95.84%, specificity of 90.08%, and an accuracy of 94.14%. The proposed method stands out, with a sensitivity of 94.28%, the highest specificity at 99.29%, and an accuracy of 98.25%, indicating its superior performance in balancing both true-positive and true-negative rates while maintaining high overall accuracy.

The experimental analysis highlights several key factors contributing to the success of the proposed methodology.

• By integrating the modalities of brain MRI tumor images based on the NSLP followed by the fusion strategies, the presented model significantly detects abnormal regions within the brain tumors. Unlike relying on individual imaging sequences, the fusion process enhances tissue information, enabling a more accurate detection of tumor regions. This fusion-based enhancement is a significant advantage of the proposed technique;
• Furthermore, the proposed brain tumor classification methodology outperforms existing techniques by accurately distinguishing LG and HG gliomas from MRI images. This is achieved through an efficient extraction strategy that is TV-L1 decomposition followed by LBP. Here, the TV-L1 identifies crucial details, like patterns and structural features of the images, whereas the LBP provides the edge and corner features. Together, these approaches represent a major contribution of the proposed method, enabling precise and reliable tumor classification.

5. Conclusions and Future Scope

In this work, we suggested a novel approach to differentiate LG and HG gliomas from MRI scans. Here, at first, Gaussian filtering was applied to minimize unwanted artifacts. Then, we utilized the NSLP with PCA and averaging image fusion technique to enhance the overall performance of tumor identification by effectively combining the modalities of brain MRI images. Further, for an effective classification, we extracted texture details from fused images based on the TV-L1 decomposition and LBP. Finally, these extracted features were applied to various supervised ML classifiers, such as SVM, KNN, DT, AdaBoost, and LogitBoost, to distinguish LG and HG gliomas. From the experimental results, it is evident that the developed framework surpasses the existing techniques in accurately identifying LG and HG gliomas. Hence, we conclude that our model offers a reliable and efficient tool for MRI-based brain tumor classification. In the future, we will extend our work to multiclass problems.