Transport Optimization in the Supply Chain Using the Ant Colony Algorithm †
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Software Used
2.2. Method
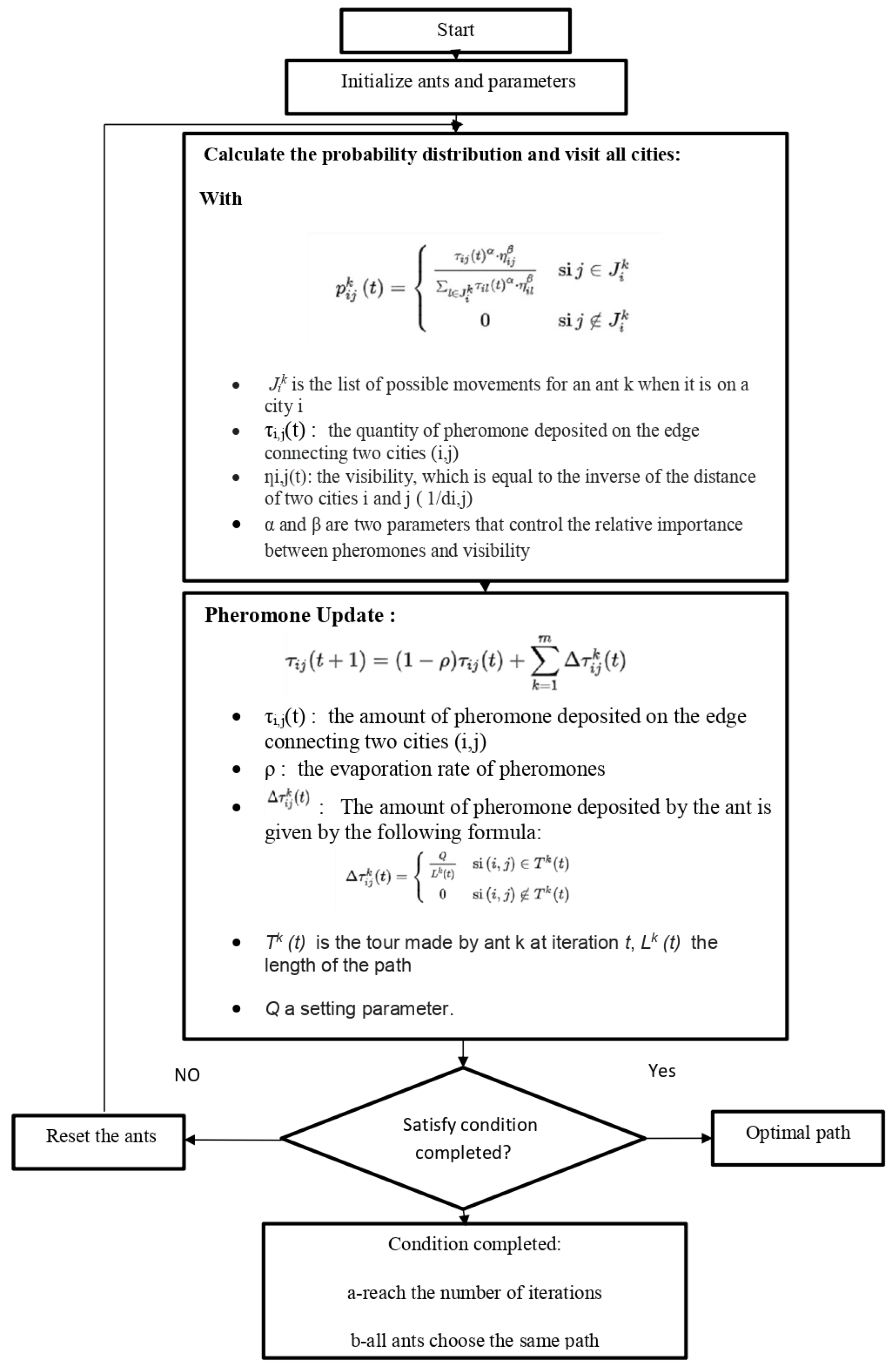
Ant Colony Algorithm
3. Results and Discussion
3.1. Evaluation Test
- The number of ants is equal to the number of subcontractors equal to 5;
- The parameters α and β are equal to 1;
- The initial pheromone is τi,j(0) = 2; Q = 100.
- Step 1: Calculate the paths taken for each ant.
- Step 2: Update the pheromones by applying the following formula:
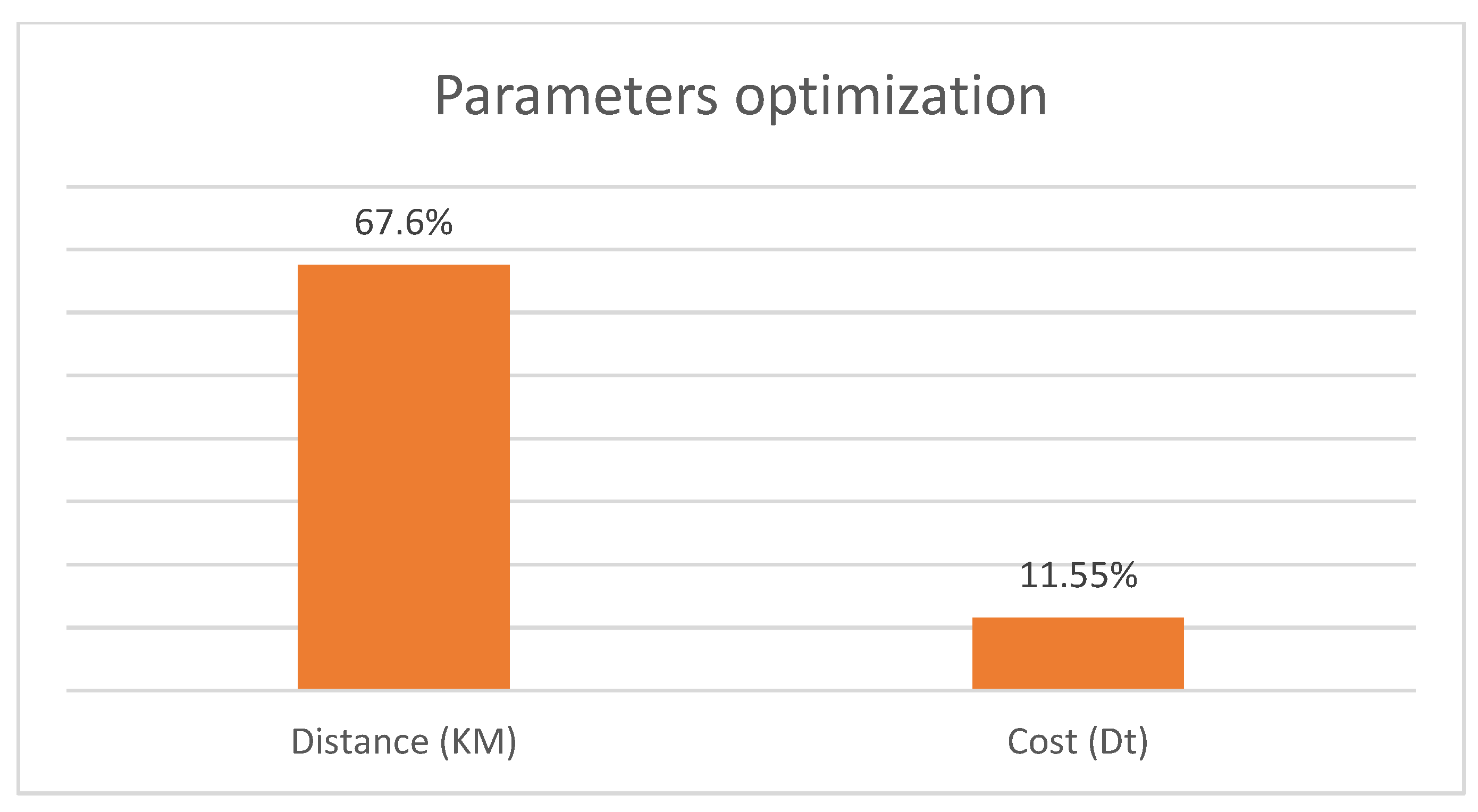
3.2. Statistical Study and Analysis Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Noto, M.; Sato, H. A method for the shortest path search by extended Dijkstra algorithm. In Proceedings of the SMC 2000 Conference Proceedings, 2000 IEEE International Conference on Systems, Man and Cybernetics, ’Cybernetics Evolving to Systems, Humans, Organizations, and Their Complex Interactions, Nashville, TN, USA, 8–11 October 2000; pp. 2316–2320. [Google Scholar]
- Sung, S.W.; Jang, Y.J. Heuristic for the assort-packing and distribution problem in the fashion apparel industry. Int. J. Prod. Res. 2018, 56, 3116–3133. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, J.; Ou, G.; Liu, H. Coordinated Optimization of Production and Delivery Operations in Apparel Supply Chains Using a Hybrid Intelligent Algorithm. In Proceedings of the International Conference on Artificial Intelligence on Textile and Apparel, Hongkong, China, 3–6 July 2018; pp. 9–15. [Google Scholar]
- Yu, W.; Lu, L. A route planning strategy for the automatic garment cutter based on genetic algorithm. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 379–386. [Google Scholar]
- Koopahi, M.; Kiani, G. Optimal transportation schedule of wheat using mathematical models. Iran. J. Agric. Sci. 2006, 37, 127–135. [Google Scholar]
- Clement, M. AI-Driven Predictive Analytics for Supply Chain Optimization in Textile Manufacturing. 2025. Available online: https://www.researchgate.net/publication/390489029_AI-Driven_Predictive_Analytics_for_Supply_Chain_Optimization_in_Textile_Manufacturing (accessed on 29 May 2025).
- Wang, D.; Peng, X.; Qin, H. Improved genetic algorithm for optimizing flexible workshop scheduling. In Proceedings of the International Conference on Mechatronics and Intelligent Control (ICMIC 2024), Changsha, China, 18–20 September 2025; SPIE: Bellingham, WA, USA, 2025; Volume 13447, pp. 475–485. [Google Scholar]
- Sun, Y.; Lang, M.; Wang, D. Optimization models and solution algorithms for freight routing planning problem in the multi-modal transportation networks: A review of the state-of-the-art. Open Civ. Eng. J. 2015, 9, 714–723. [Google Scholar] [CrossRef]
- Farahmand-Tabar, S.; Afrasyabi, P. Multi-modal Routing in Urban Transportation Network Using Multi-objective Quantum Particle Swarm Optimization. In Applied Multi-Objective Optimization; Springer Nature Singapore: Singapore, 2024; pp. 133–154. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M.; Gambardella, L.M. Ant colonies for the travelling salesman problem. Biosystems 1997, 43, 73–81. [Google Scholar] [CrossRef] [PubMed]
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 0 | 2 | 10 | 8 | 3 |
| B | 1 | 0 | 2 | 5 | 7 |
| C | 9 | 1 | 0 | 3 | 6 |
| D | 10 | 4 | 3 | 0 | 2 |
| E | 2 | 7 | 5 | 1 | 0 |
| k | Lk | Δτi,jk |
|---|---|---|
| 1 | 11 | 9.1 |
| 2 | 9 | 11.1 |
| 3 | 9 | 11.1 |
| 4 | 11 | 9.1 |
| 5 | 9 | 11.1 |
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 0 | 19.2 | 1 | 1 | 34.3 |
| B | 34.3 | 0 | 19.2 | 1 | 1 |
| C | 1 | 34.3 | 0 | 3 | 1 |
| D | 1 | 1 | 34.3 | 0 | 19.2 |
| E | 19.2 | 1 | 1 | 34.3 | 0 |
| The Path Traveled by Each Ant | Length Path (KM) |
|---|---|
| A, E, D, C, B, A | 9 |
| B, A, E, D, C, B | 9 |
| C, B, A, E, D, C | 9 |
| D, C, B, A, E, D | 9 |
| E, D, C, B, A, E | 9 |
| Technician’s Results | Ant Colony Results | |||||
|---|---|---|---|---|---|---|
| Path | The Path Traveled by a Technician | Path Length (KM) | Cost (dt) | The Path Traveled by Each Ant | Path Length (KM) | Cost |
| A→A | A, B, E, C, D, A | 27 | 25.37 | A, E, D, C, B, A | 9 | 22.44 |
| B→B | B, D, C, A, E, B | 27 | 25.37 | B, A, E, D, C, B | 9 | 22.44 |
| C→C | C, A, D, E, B, C | 28 | 25.37 | C, B, A, E, D, C | 9 | 22.44 |
| D→D | D, A, C, B, E, D | 29 | 25.37 | D, C, B, A, E, D | 9 | 22.44 |
| E→E | E, B, D, A, C, E | 28 | 25.37 | E, D, C, B, A, E | 9 | 22.44 |
| Indicator | Technician | ACO (Ant Colony Optimization) |
|---|---|---|
| Average Distance (km) | 27.8 km | 9 km |
| Average Cost (dt) | 25.37 dt | 22.44 dt |
| Standard Deviation (Distance) | ≈0.748 km | 0 km |
| Standard Deviation (Cost) | 0 dt (fixed cost) | 0 dt (same for all ants) |
| Min/Max Distance | 27 km/29 km | 9 km/9 km |
| Min/Max Cost | 25.37 dt/25.37 dt | 22.44 dt/22.44 dt |
| Performance Gain | — | +67.6% (distance), +11.55% (cost) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lahdhiri, M.; Jmali, M.; Babay, A.; Hlyal, M. Transport Optimization in the Supply Chain Using the Ant Colony Algorithm. Eng. Proc. 2025, 97, 56. https://doi.org/10.3390/engproc2025097056
Lahdhiri M, Jmali M, Babay A, Hlyal M. Transport Optimization in the Supply Chain Using the Ant Colony Algorithm. Engineering Proceedings. 2025; 97(1):56. https://doi.org/10.3390/engproc2025097056
Chicago/Turabian StyleLahdhiri, Mourad, Mohamed Jmali, Amel Babay, and Mustapha Hlyal. 2025. "Transport Optimization in the Supply Chain Using the Ant Colony Algorithm" Engineering Proceedings 97, no. 1: 56. https://doi.org/10.3390/engproc2025097056
APA StyleLahdhiri, M., Jmali, M., Babay, A., & Hlyal, M. (2025). Transport Optimization in the Supply Chain Using the Ant Colony Algorithm. Engineering Proceedings, 97(1), 56. https://doi.org/10.3390/engproc2025097056






