Predicting Color Change of Cotton Fabric After Biopolishing Treatment Using Fuzzy Logic Modeling †
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Equipment
2.2. Methods
3. Development of Fuzzy Expert System
3.1. Structure of Fuzzy Expert System
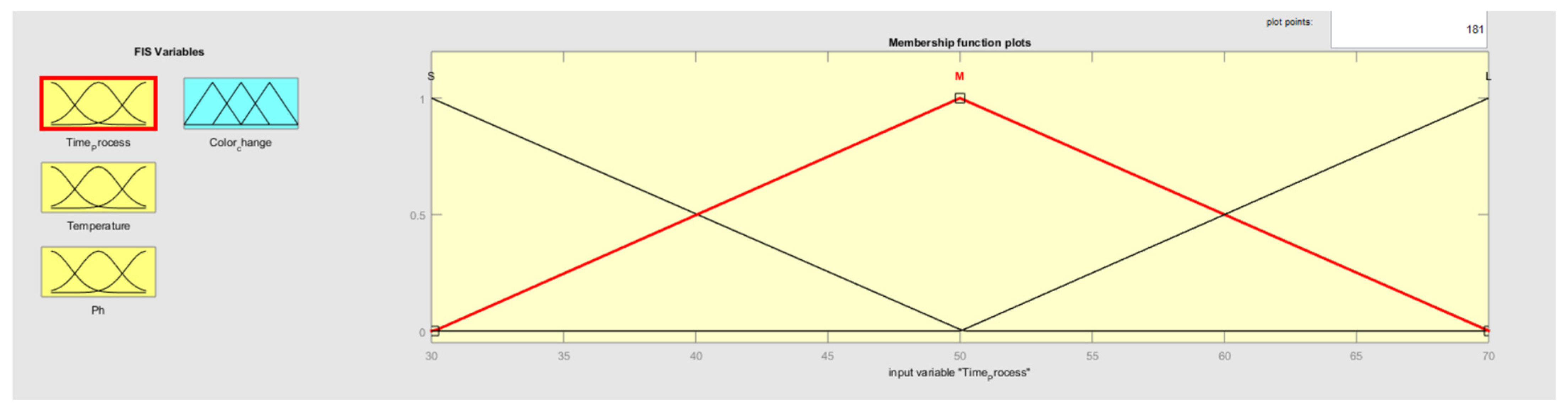
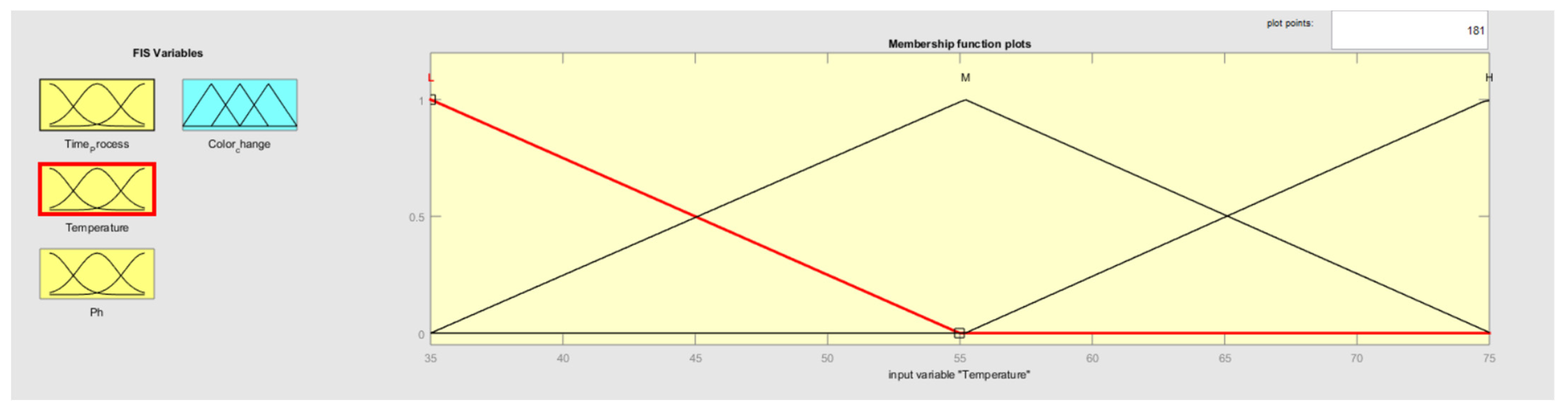
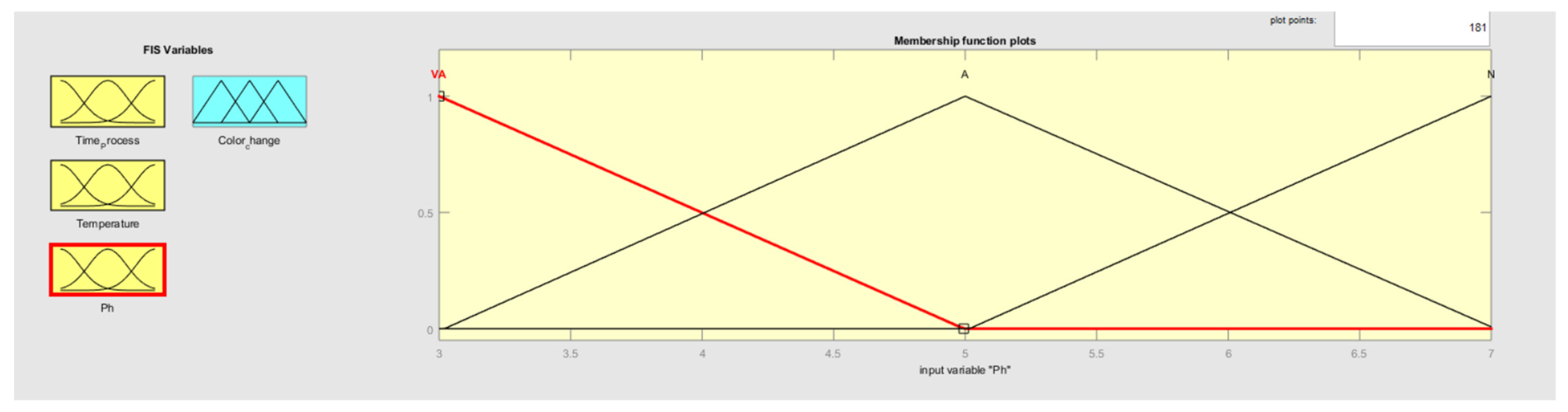
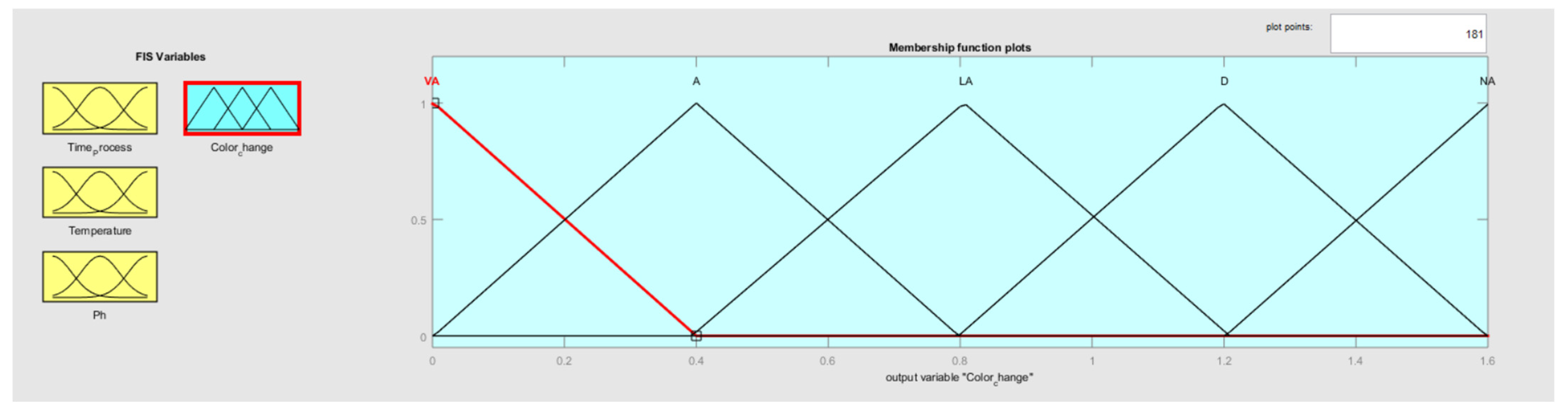
3.2. Fuzzification Interfaces
3.3. Knowledge Base
3.4. Decision-Making Logic
3.5. Defuzzification
4. Implementation of Fuzzy Expert System
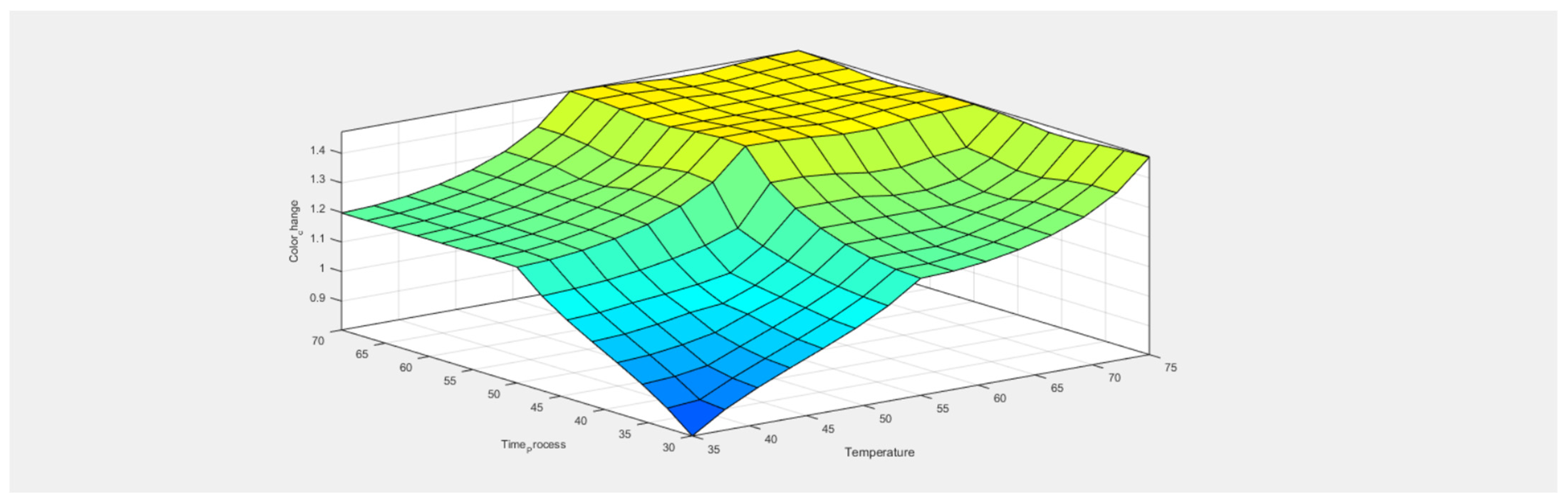
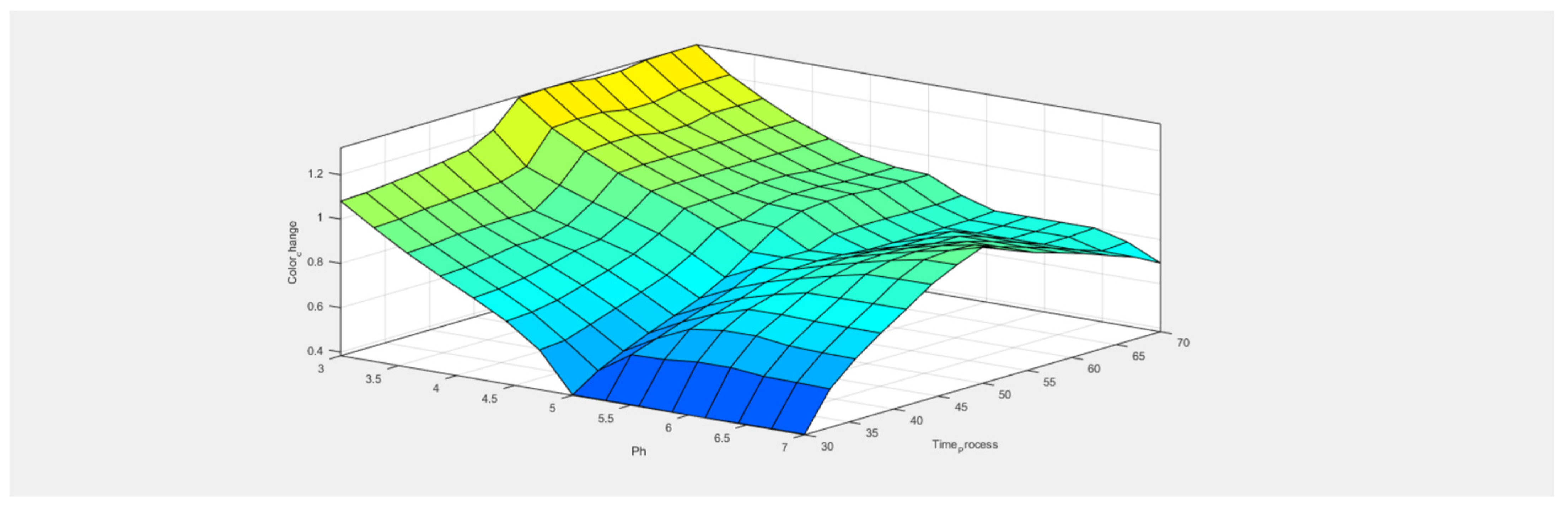
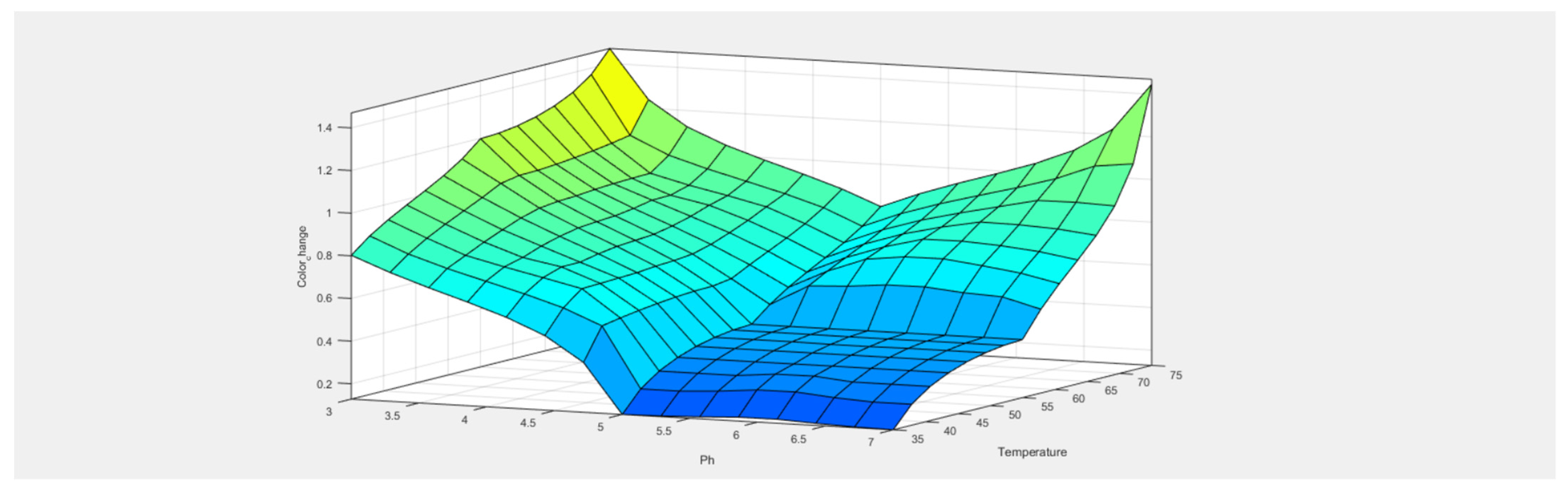
5. Results and Discussion
6. Economic Impact
7. Discussion of the Limits
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, Y.; Sun, Z.; Guo, X.; Zhou, Y.; Jiang, L.; Chen, S.; Ma, J. Study on enzyme washing process of hemp organic cotton blended fabric. Int. J. Cloth. Sci. Technol. 2019, 31, 58–64. [Google Scholar] [CrossRef]
- Sharma, A.; Tewari, R.; Rana, S.S.; Soni, R.; Soni, S.K. Cellulases: Classification, Methods of Determination and Industrial Applications. Appl. Biochem. Biotechnol. 2016, 179, 1346–1380. [Google Scholar] [CrossRef] [PubMed]
- Gias Uddin, M. Effect of Biopolishing on Dye ability of Cotton Fabric—A Review. Trends Green Chem. 2016, 2, 1–5. [Google Scholar] [CrossRef]
- Buschle-Diller, G.; Traore, M.K. Influence of Direct and Reactive Dyes on the Enzymatic Hydrolysis of Cotton. Text. Res. J. 1998, 68, 185–192. [Google Scholar] [CrossRef]
- Mori, R.; Haga, T.; Takacishi, T. Reactive dye dyeability of cellulose fibers with cellulase treatment. J. Appl. Polym. Sci. 2003, 61, 199. [Google Scholar] [CrossRef]
- Jevšnik, S.; Fakin, D.; Heikinheimo, L.; Stjepanovič, Z. Changes in a knitted fabric’s surface properties due to enzyme treatments. Fibers Polym. 2012, 13, 371–379. [Google Scholar] [CrossRef]
- Sen, A.; Kapila, R.; Chaudhary, S.; Nigam, A. Biotechnological Applications of Microbial Enzymes to Replace Chemicals in the Textile Industry—A Review. J. Text. Assoc. 2021, 82, 68–73. [Google Scholar]
- Toprak, T.; Anis, P. Combined one-bath desizing–scouring–depilling enzymatic process and effect of some process parameters. Cellulose 2017, 24, 383–394. [Google Scholar] [CrossRef]
- Saravanan, D.; Vasanthi, N.S.; Ramachandran, T. A review on influential behaviour of biopolishing on dyeability and certain physico-mechanical properties of cotton fabrics. Carbohydr. Polym. 2009, 76, 1–7. [Google Scholar] [CrossRef]
- Das, S.C.; Uddin, M.A. A Qualitative Testing method for assessing Enzymatic biopolishing effect on Textile substrate. In Proceedings of the 1st International Conference On Textile Science & Engineering, Dhaka, Bangladesh, 19–20 January 2023; pp. 77–85. [Google Scholar]
- Kane, F.; Shen, J.; Morgan, L.; Prajapati, C.; Tyrer, J.; Smith, E. Innovative Technologies for Sustainable Textile Coloration, Patterning, and Surface Effects. In Sustainability in the Textile and Apparel Industries; Springer: Cham, Switzerland, 2020; pp. 99–127. [Google Scholar]
- Mishra, V.; Agarwal, S.M.; Puri, N. COMPREHENSIVE AND COMPARATIVE ANALYSIS OF NEURAL NETWORK. Int. J. Comput. Appl. 2018, 2. [Google Scholar] [CrossRef]
- Stojčić, M. Application of the ANFIS model in road traffic and transportation: A literature review from 1993 to 2018. Oper. Res. Eng. Sci. Theory Appl. 2018, 1, 40–61. [Google Scholar] [CrossRef]
- Chevrier, R.; Castex, E.; Josselin, D.; Canalda, P.; Chatonnay, P. Un algorithme génétique pour le transport à la demande en convergence. Revue Internationale de Géomatique 2008, 18, 239–265. [Google Scholar] [CrossRef]
- Hassan, M.N.; Fariha, F.T.; Zayee, Z.; Hasan, M. Analyzing different functional and dyeing performance of natural blended fabric utilizing natural dyes and quality prediction by fuzzy logic. Heliyon 2024, 10, e40399. [Google Scholar] [CrossRef] [PubMed]
- Haji, A.; Payvandy, P. Application of ANN and ANFIS in prediction of color strength of plasma-treated wool yarns dyed with a natural colorant. Pigment Resin Technol. 2020, 49, 171–180. [Google Scholar] [CrossRef]
- Taghinezhad, E.; Kaveh, M.; Szumny, A. Optimization and prediction of the drying and quality of turnip slices by convective-infrared dryer under various pretreatments by rsm and anfis methods. Foods 2021, 10, 284. [Google Scholar] [CrossRef]
- Hossain, I.; Hossain, A.; Choudhury, I.A.; Bakar, A.; Shahid, A. Color Strength Modeling of Knitted Fabrics Using Fuzzy Logic Approach. In Proceedings of the International Conference on Mechanical, Industrial and Materials Engineering 2013 (ICMIME2013), Rahshahi, Bangladesh, 1–3 November 2013; pp. 1–3. [Google Scholar]
- Azanaw, A.; Ketema, A. Process Optimization for Biosingeing of 100% Cotton Terry Towel Fabric Using Box-Behnken Design. Adv. Mater. Sci. Eng. 2022, 2022, 6920864. [Google Scholar] [CrossRef]
- Gómez-Polo, C.; Muñoz, M.P.; Lorenzo Luengo, M.C.; Vicente, P.; Galindo, P.; Martín Casado, A.M. Comparison of the CIELab and CIEDE2000 color difference formulas. J. Prosthet. Dent. 2016, 115, 65–70. [Google Scholar] [CrossRef]
- Moussa, A.; Dupont, D.; Steen, D.; Zeng, X. Multiangle study on color of textile structures. Color Res. Appl. 2009, 34, 274–284. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic. In Comput Complex; Meyers, R., Ed.; Springer: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Sarkar, J.; Mondal, M.S.; Khalil, E. Predicting fabric GSM and crease recovery angle of laser engraved denim by fuzzy logic analysis. J. Eng. Appl. Sci. 2020, 4, 52–64. [Google Scholar]
- Kim, T.Y.; Lee, S.H. Combustion and Emission Characteristics of Wood Pyrolysis Oil-Butanol Blended Fuels in a Di Diesel Engine. Int. J. Automot. Technol. 2015, 16, 903–912. [Google Scholar] [CrossRef]
- Phuong, N.H.; Kreinovich, V. Fuzzy Logic and its Applications in Medicine. Int. J. Med. Inform. 2001, 62, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Jane, J.B.; Ganesh, E.N. A review on big data with machine learning and fuzzy logic for better decision making. Int. J. Sci. Technol. Res. 2019, 8, 1121–1125. [Google Scholar]
- Chakraverty, S.; Sahoo, D.M.; Mahato, N.R. Concepts of Soft Computing: Fuzzy and ANN with Programmingd; Springer: Singapore, 2019; pp. 1–195. [Google Scholar]
- Imprialou, M.I.M.; Quddus, M.; Pitfield, D.E. High accuracy crash mapping using fuzzy logic. Transp. Res. Part C Emerg. Technol. 2014, 42, 107–120. [Google Scholar] [CrossRef]


| Process Parameters | Values |
|---|---|
| Number of samples | 27 |
| Dye concentration (% o.w.f) | 1.5 |
| Alkali concentration (g/L) | 15 |
| Salt concentration (g/L) | 65 |
| Time (min) | 60 |
| Temperature (°C) | 60 |
| Liquor ratio | 8 |
| Process Parameters | Values | ||
|---|---|---|---|
| Cellulase concentration (%.o.w.f) | 2 | ||
| Time process (min) | 30 | 50 | 70 |
| Temperature (°C) | 35 | 55 | 75 |
| Ph value | 3 | 5 | 7 |
| Liquor ratio | 8 | ||
| Rules | Input Variables | Output Variables | ||
|---|---|---|---|---|
| Ph | TP | TC | CC | |
| 1 | VA | S | L | BA |
| 2 | VA | S | M | NA |
| 5 | A | S | L | VA |
| 26 | N | M | H | NA |
| 27 | N | L | H | NA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mostafa, E.; Mhammed, E.; Redouan, M.; Cherkaoui, O.; Soulhi, A. Predicting Color Change of Cotton Fabric After Biopolishing Treatment Using Fuzzy Logic Modeling. Eng. Proc. 2025, 97, 40. https://doi.org/10.3390/engproc2025097040
Mostafa E, Mhammed E, Redouan M, Cherkaoui O, Soulhi A. Predicting Color Change of Cotton Fabric After Biopolishing Treatment Using Fuzzy Logic Modeling. Engineering Proceedings. 2025; 97(1):40. https://doi.org/10.3390/engproc2025097040
Chicago/Turabian StyleMostafa, Elkhaoudi, Elbakkali Mhammed, Messnaoui Redouan, Omar Cherkaoui, and Aziz Soulhi. 2025. "Predicting Color Change of Cotton Fabric After Biopolishing Treatment Using Fuzzy Logic Modeling" Engineering Proceedings 97, no. 1: 40. https://doi.org/10.3390/engproc2025097040
APA StyleMostafa, E., Mhammed, E., Redouan, M., Cherkaoui, O., & Soulhi, A. (2025). Predicting Color Change of Cotton Fabric After Biopolishing Treatment Using Fuzzy Logic Modeling. Engineering Proceedings, 97(1), 40. https://doi.org/10.3390/engproc2025097040






