Performance Analysis of Double-Layered Thin-Walled Hemispherical Shell Structures Under Quasi-Static Compression †
Abstract
1. Introduction
2. Experimental Methodology
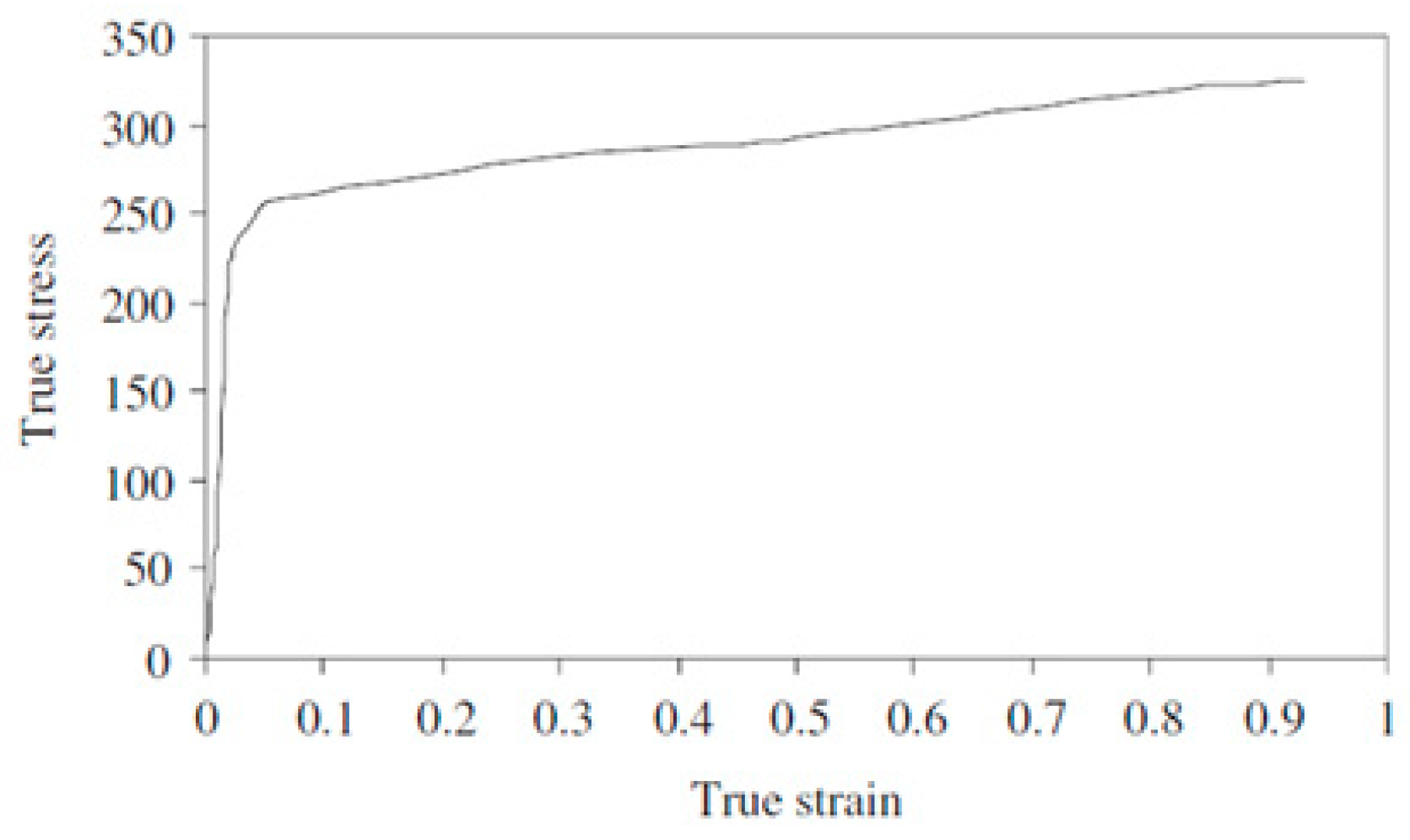
3. Numerical Methodology and Validation
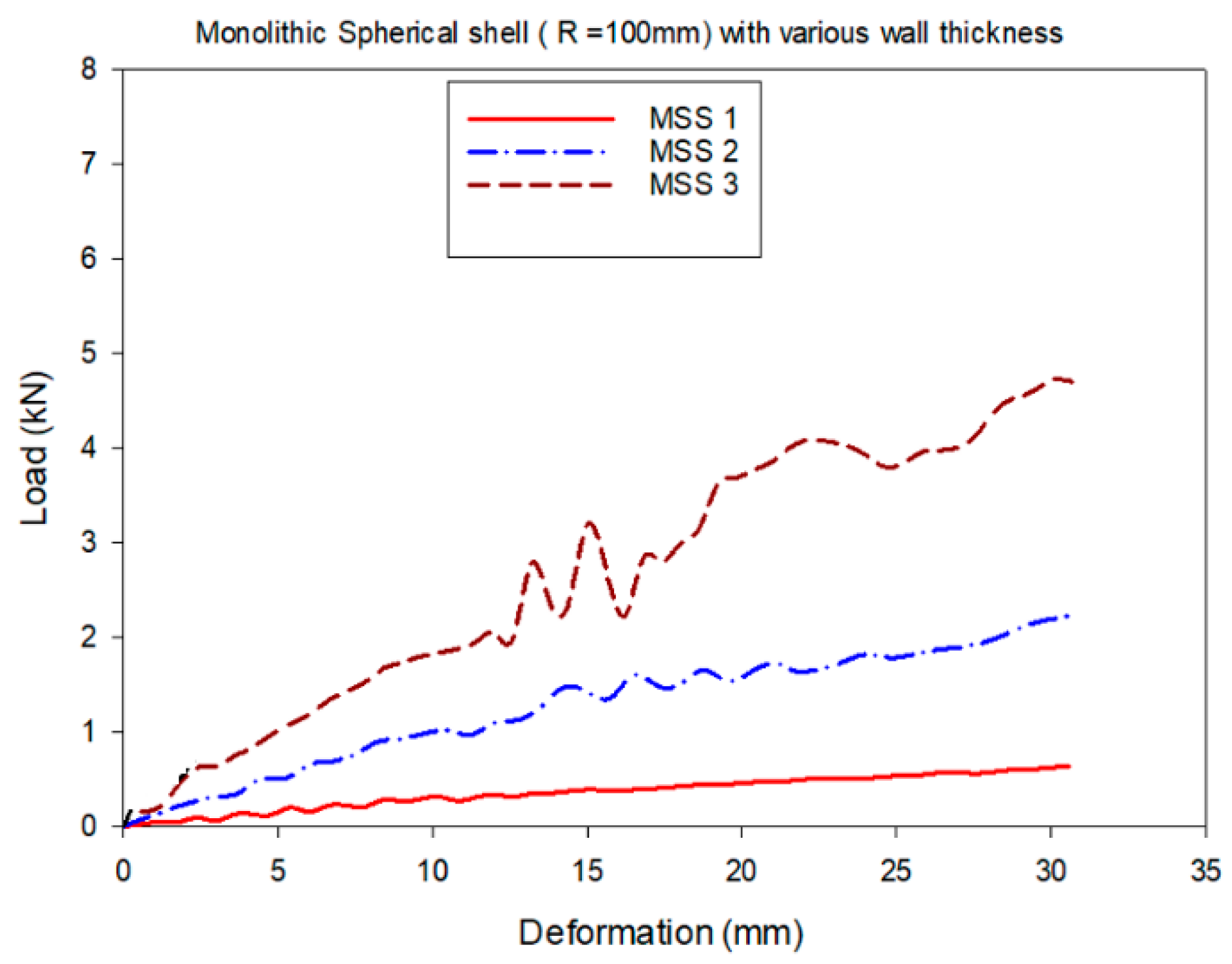
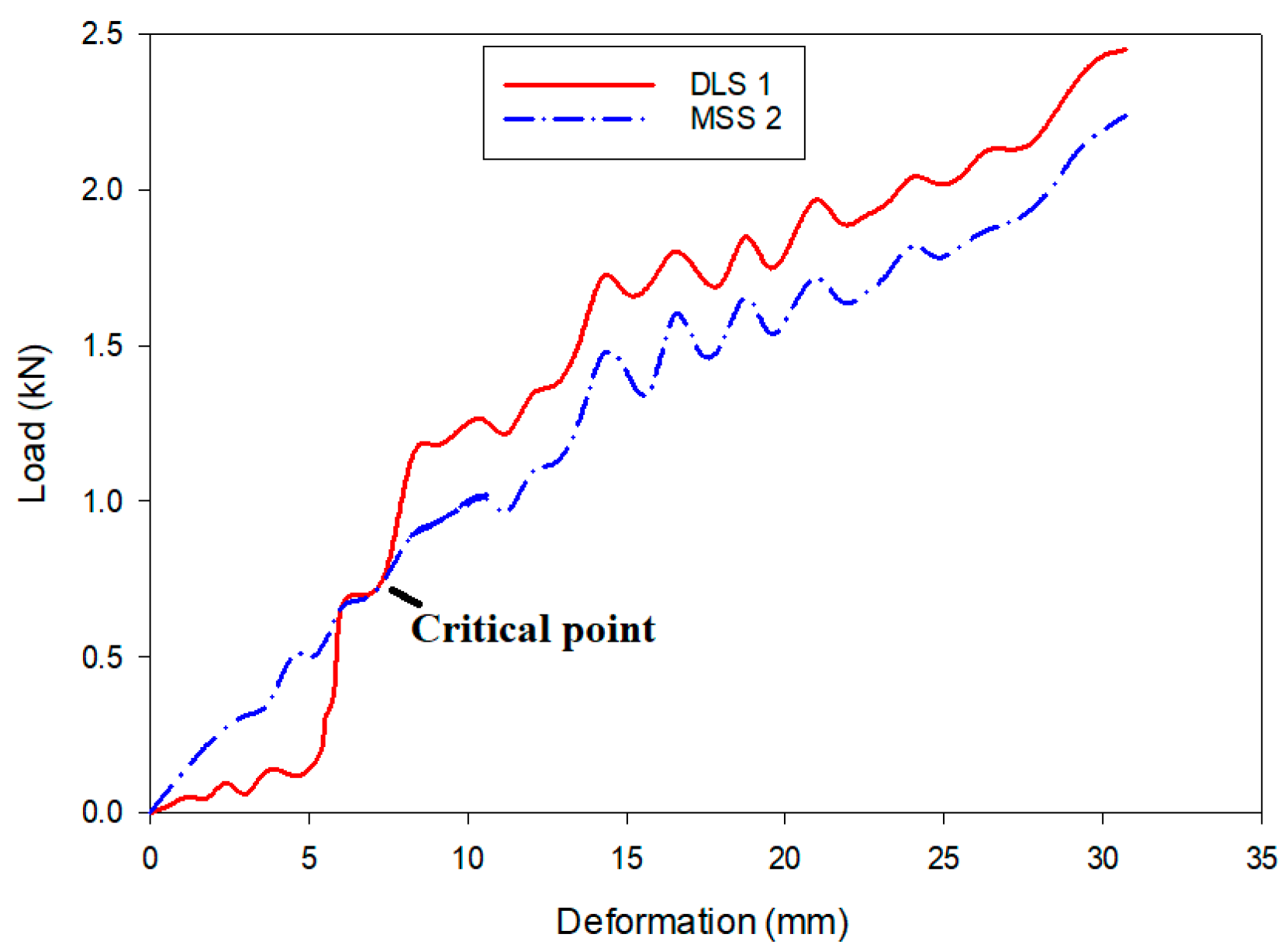
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gupta, N.K.; Sheriff, N.M.; Velmurugan, R. Experimental and numerical investigations into collapse behaviour of thin spherical shells under drop hammer impact. Int. J. Solids Struct. 2007, 44, 3136–3155. [Google Scholar] [CrossRef]
- Gupta, N.K.; Sheriff, N.M.; Velmurugan, R. Experimental and theoretical studies on buckling of thin spherical shells under axial loads. Int. J. Mech. Sci. 2008, 50, 422–432. [Google Scholar] [CrossRef]
- Karagiozova, D.; Zhang, X.; Yu, T.X. Static and dynamic snap-through behaviour of an elastic spherical shell. Acta Mech. Sin. 2012, 28, 695–710. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, R.; Yu, T.X. Experimental study on static/dynamic local buckling of ping pong balls compressed onto a rigid plate. In Proceedings of the Fourth International Conference on Experimental Mechanics, Singapore, 18–20 November 2009; Quan, C., Ed.; SPIE Press: Bellingham, WA, USA, 2010. [Google Scholar]
- Dong, X.; Gao, Z.; Yu, T.X. Dynamic crushing of thin-walled spheres: An experimental study. Int. J. Impact Eng. 2008, 35, 717–726. [Google Scholar] [CrossRef]
- Morris, E.; Olabi, A.G.; Hashmi, M.S.J. Analysis of nested tube type energy absorbers with different indenters and exterior constraints. Thin Walled Struct. 2006, 44, 872–885. [Google Scholar] [CrossRef]
- Baroutaji, A.; Gilchrist, M.D.; Olabi, A.G. Quasi-static, impact and energy absorption of internally nested tubes subjected to lateral loading. Thin Walled Struct. 2016, 98, 337–350. [Google Scholar] [CrossRef]
- Morris, E.; Olabi, A.G.; Hashmi, M.S.J. Lateral crushing of circular and non-circular tube systems under quasi-static conditions. J. Mater. Process. Technol. 2007, 191, 132–135. [Google Scholar] [CrossRef]
- Designation, E. Standard Test Methods for Tension Testing of Metallic Materials; ASTM: West Conshohocken, PA, USA, 2001. [Google Scholar]
- Dassault Systèmes, SIMULIA Corp. Abaqus Analysis User’s Manual, Version 6.14, Dassault Systèmes, SIMULIA Corp.: Providence, RI, USA, 2014.





| Specimen | Radius | Depth (mm) | Thickness (t) | Specimen | Radius (R) (mm) | Thickness (t) (mm) | ||
|---|---|---|---|---|---|---|---|---|
| Inner | Outer | Inner | Outer | |||||
| MSS 1 | 100 | 100 | 0.5 | DLS 1 | 99.5 | 100 | 0.5 | 0.5 |
| MSS 2 | 100 | 100 | 1.0 | DLS 2 | 99 | 100 | 0.5 | 1.0 |
| MSS 3 | 100 | 100 | 1.5 | DLS 3 | 99.5 | 100 | 1.0 | 0.5 |
| Geometry | Radius of Parallel Circle (mm) | EA(kJ) | ||||
|---|---|---|---|---|---|---|
| Expt | Software | % Variation | Expt | Software | % Variation | |
| MSS 1 | 67.1 | 70.2 | 4.41 | 54.6 | 56.2 | 2.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed Ismail, N.M.; Sudha Ramakrishnan, K. Performance Analysis of Double-Layered Thin-Walled Hemispherical Shell Structures Under Quasi-Static Compression. Eng. Proc. 2025, 93, 20. https://doi.org/10.3390/engproc2025093020
Mohamed Ismail NM, Sudha Ramakrishnan K. Performance Analysis of Double-Layered Thin-Walled Hemispherical Shell Structures Under Quasi-Static Compression. Engineering Proceedings. 2025; 93(1):20. https://doi.org/10.3390/engproc2025093020
Chicago/Turabian StyleMohamed Ismail, Nalla Mohamed, and Kavin Sudha Ramakrishnan. 2025. "Performance Analysis of Double-Layered Thin-Walled Hemispherical Shell Structures Under Quasi-Static Compression" Engineering Proceedings 93, no. 1: 20. https://doi.org/10.3390/engproc2025093020
APA StyleMohamed Ismail, N. M., & Sudha Ramakrishnan, K. (2025). Performance Analysis of Double-Layered Thin-Walled Hemispherical Shell Structures Under Quasi-Static Compression. Engineering Proceedings, 93(1), 20. https://doi.org/10.3390/engproc2025093020






