Abstract
This review paper explores the properties of graphene-based transparent electrodes for space solar cell applications. The space environment is extreme due to high-energy radiation, high vacuum and alternating temperature, which are responsible for damaging the atomic structure of materials, and so it influences the performance of a device. In this context, using a physical description of graphene, we analyze its electrical and optical properties, like transmittance and sheet resistance, in order to obtain innovative transparent electrodes that can perform in extreme conditions. In this sense, graphene can be a good candidate for this kind of application.
1. Introduction
In this work, a preliminary analysis, through a literature study, is conducted on several aspects to realize the new generation of photovoltaic applications for extreme environments like space.
It is known that the space environment has different characteristics that can influence the performance of photovoltaic solar cells. In particular, strong radiation, composed of high-energy particles, is known to cause atomic defects in a material, and it can reduce the performance of a device in terms of efficiency. Moreover, the space environment is also characterized by high vacuum and alternating temperatures, which cause the material to become more exposed to radiation.
Graphene is a promising 2D quantum material, which has some interesting electrical and optical properties, like transparency and a strong interaction with light.
Historically, it has been used for transparent electrodes made of indium thin oxide (ITO), a material with high transparency in the solar spectrum. Nowadays, ITO is very expensive due to low indium availability, so it is possible to replace it with graphene.
In the work, we offer a physical description of the ground-state properties of graphene, given by the solution of the “Massless Dirac Fermion” (MDF) model [1] and the analysis of the Quantum Hall effect phenomenon [2].
From there, it is possible to obtain properties like high transmittance and low sheet resistance, which are the main requirements for a transparent electrode.
This kind of analysis is important in order to understand the effects of the space environment on graphene and what characteristics space solar cells must have in order to perform in these conditions.
This represents a good starting point for space photovoltaic applications because, as shown in the literature, graphene exhibits good behavior in the space environment.
2. Space Environment and Specific Requirements for Space Solar Cells
The space environment is characterized by three main apects: strong radiation, high vacuum and alternating temperature (Figure 1) [3].
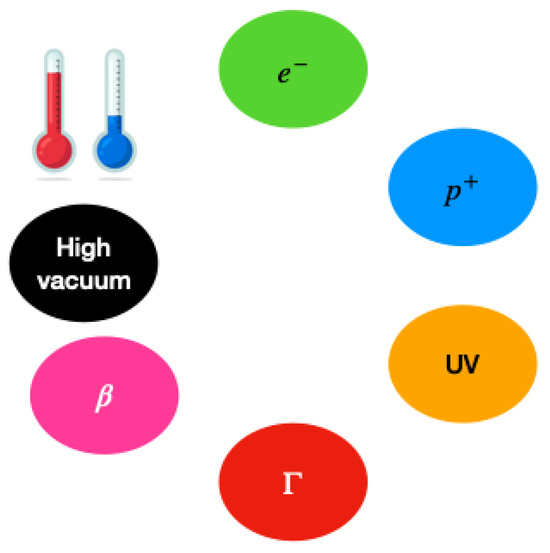
Figure 1.
Space environment characteristics.
Strong radiation is formed by high-energy particles, like electrons, protons, UV rays, rays, rays and X rays. These particles are known to damage materials due to their high energy and for this reason are called “shadow killers”.
Electron radiation affects the dielectric properties of a material; in particular, defects are created in the crystal of the semiconductor of the solar cell. As a consequence of this, a minority-carrier recombination center or a majority-carrier trap center takes place.
Proton radiation is a kind of ionizing particle radiation, coming from both galactic cosmic radiation and solar flares. It is common in the orbit of aircraft around the Earth. Protons with energy close to 1 MeV have a high stopping cross-section, and they cause a lot of damage to a material because the mass of the proton is 2000 times bigger than that of the electron. In particular, most of the damage caused by proton radiation is evident in the short-circuit current of the solar cell (), which decreases, while the open-circuit voltage () and the fill factor (FF) remain constant, as shown in [3].
UV rays are known to deteriorate materials, and it is crucial to find a way to enhance UV photostability. A way could be to integrate photovoltaic materials with photoluminescent materials in solar cell applications in order to convert high-energy photons into low-energy photons.
rays come from nuclear fusion at the core of stars. Earth is protected by its own atmosphere, so they can be detected only in space. When they interact with a material, due to the photoelectric effect and Compton scattering, the short-circuit current of the solar cell decreases.
X rays are electromagnetic with a short wavelength between that of UV and rays. They do not cause damage to materials.
In addition to the problems related to radiation, the space environment also has high vacuum and alternating temperatures.
High vacuum is caused by a decrease in atmospheric pressure induced by an increase in the distance of an object from the ground. In particular, it is important to investigate high vacuum with light illumination. Light may produce degradation in a material, and it is important to understand the mechanism of degradation under illumination. Different experiments have been performed under ultrahigh-vacuum illumination (UHV) and they are reported in [3].
In the space environment, temperature changes directly from high values to low values due to the sunlight. Changes from 100 to 130 °C with sunlight to ‒200–150 °C without sunlight have been observed. This has an effect on the electrical properties of a material, like resistance and transport.
For the reasons listed above, it is important that space solar cells have some specific requirements.
First of all, they should have high performances because they must operate over a wide range of temperatures and sunlight intensities in the space environment. Moreover, space solar cells should have good tolerance to radiation damages.
Another requirement for space solar cells is high specific power. In order to prevent degradation, it is common to apply layers of protective materials, like glass, to screen the solar cell from radiation. This, inevitably, increases the load weight, so high specific power is very important.
In addition, since it is very difficult to repair space solar cells, another necessity for them is long-term stability.
3. Physical Description of Graphene
Graphene is a 2D quantum material that shows a lot of interesting properties. It is composed of a layer of carbon atoms arranged in a hexagonal honeycomb lattice (Figure 2).
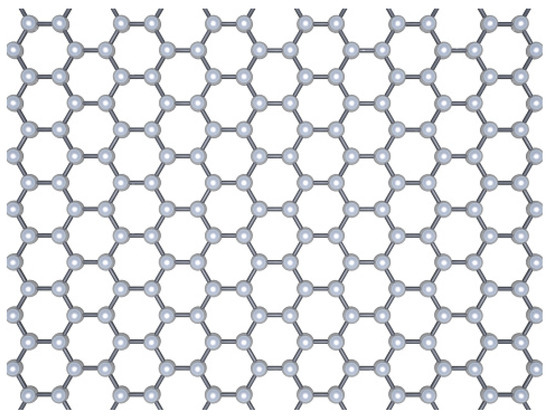
Figure 2.
Atomic structure of graphene.
From the point of view of quantum mechanics, it can be described by the MDF model. The reason for the name of the model comes from the fact that the effective mass of the electrons in graphene is close to zero, so they act as relativistic particles, which are described by the Dirac equation. The Hamiltonian of the model is the following:
in which is the Fermi velocity, is the 2D Pauli matrix and is the quasiparticle momentum. Let us put the Hamiltoninan in (1) into matricial form:
where
are the Pauli matrix. The eigenvalues of Matrix (2) give the ground-state energy of the model:
These eigenvalues represent the dispersion bands of graphene [1].
In Figure 3, the blue curve represents the valence band, while the orange one is the conduction band. Notice that the top of the valence band touches the bottom of the conduction one, so there is no bandgap. This means that graphene acts like a conductor. Moreover, this intersection point is called the Dirac point, and around it, electrons move as relativistic particles without mass. This zone is called the Dirac cone because the bands have the shape of a double cone. To understand the electrical properties of graphene, it is important to explore the phenomenon of the Quantum Hall effect (QHE) [4].
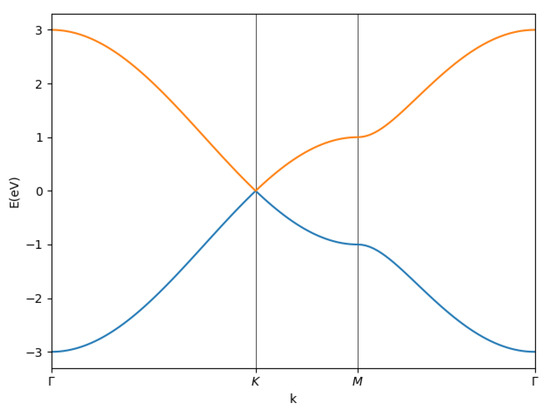
Figure 3.
Graphene dispersion bands.
To describe the QHE, an important concept is Landau levels. Consider an electron in the x-y plane in the presence of a magnetic field in the z-direction. The Hamiltonian of the system is as follows:
in which is the vector potential related to the magnetic field by . The eigenvalues of this Hamiltonian are
where is the cyclotrone frequency and is an integer number and represents the Landau level.
Another important feature useful to describe the QHE is the filling factor. This is the number of occupied Landau levels in a given magnetic field. It is defined as
In this expression, is the two-dimensional density of electrons and is the degeneracy of Landau states, in which is the flux quantum.
The filling factor can assume both integer values and fractional values. In the first case, the phenomenon is called the integer Quantum Hall effect (IQHE). The scenario refers to a system of non-interacting particles with the highest Landau level totally filled.
Figure 4 shows that the Hall resistivity has a plateau where the filling factor is an integer and the longitudinal resistivity, in the same zone, has a peak.
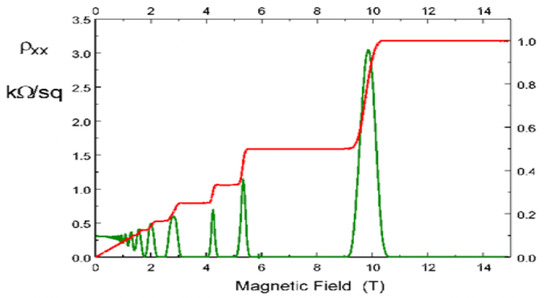
Figure 4.
Hall resistivity (red) and longitudinal resistivity (green) as function of applied magnetic field. (Adapted from [4]).
The fractional Quantum Hall effect (FQHE) takes place when the filling factor has fractional values. In this case, the system is composed by interacting electrons because the highest Landau level is partially filled. Moreover, the plot of resistivity as a function of the magnetic field also shows a plateau corresponding to these values.
The main aspect of the QHE is that electrical conductivity is quantized [2]:
4. Transmittance and Sheet Resistance in Graphene Layers
The main requirements for a transparent electrode are high transmittance and low sheet resistance [5].
Transmittance is defined as a function of frequency in the following way:
where is the optical conductivity that is quantized in graphene due to its quantum nature:
where N is the number of graphene layers. The quantization can be written in terms of the quantum of optical conductivity , so
By choosing , (9) becomes
For a rectangular sample of length L and width W, the resistance is
where is sheet resistance, is resistivity and t is the thickness of the layer. In terms of the number of graphene layers,
in which .
Generally, transmittance is expressed as a percentage, while sheet resistance is measured in , but for historical reasons, it is expressed as “Ohm per square” ().
Here, we present a plot of transmittance and sheet resistance as a function of the number of graphene N (Figure 5).
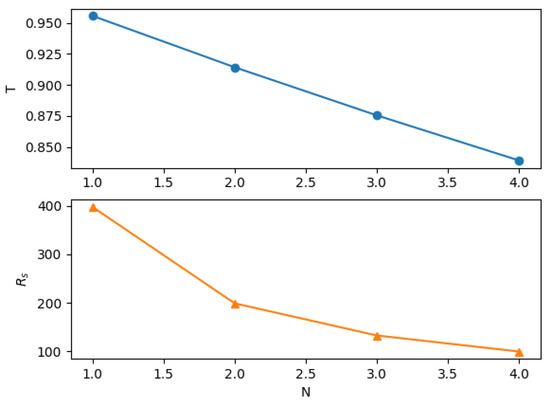
Figure 5.
Transmittance (above) and sheet resistance (below) as function of number of graphene layers.
Notice that both transmittance and sheet resistance decrease by increasing the number of graphene layers.
By eliminating the dependence on N and combining (12) and (14), it is possible to obtain how sheet resistance varies in terms of transmittance:
where is the space impedance, is the bidimensional conductivity of graphene, is electron mobility and n is the number of charge carriers.
From Figure 6, we notice that sheet resistance rises by increasing transmittance.
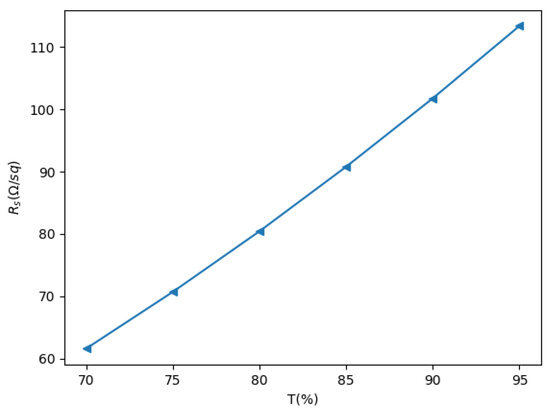
Figure 6.
Sheet resistance as function of transmittance.
Now, it is important to understand how many graphene layers to chose in a transparent electrode for photovoltaic applications. According to the previous figures, to have a good value of both transmittance and sheet resistance, the choice should be a low number of graphene layers. With a single layer, sheet resistance is too high, while with a lot of layers, transmittance is too low.
5. Challenges and Future Perspectives
To advance this analysis, it is important to investigate the physical mechanism of space solar cells under an extreme environment from a theoretical point of view. In the literature, there are some experimental results on the behavior of graphene under space radiation [6]. It is known that high-energy particles and ray radiation produce atomic displacement in materials, like lattice defects. They act as a recombination center or majority- and minority-carrier trapping centers, so they can cause a decrease in the output power of the solar cell.
Moreover, it is important to clarify the comprehensive impacts of the space environment on solar cells. Rigorous tests are necessary to understand the effects of the alternating temperature, high vacuum and space radiation.
Another important challenge is to satisfy the space photovoltaic requirements. First of all, they have to provide effective power for satellites in the future because their daily operation depends critically on space cells. Second, they should have a minimum weight in order to minimize the launch load. Third, they have to be robust and highly reliable when exposed to an extreme environment like space.
In this way, in the future, the realization of potential devices, combining graphene with other predominant technologies, like silicon, may improve the efficiency of space solar cells.
Another important challenge is to develop new materials in order to protect space solar cells from the high radiation of the space environment. An idea could be to use innovative thin glass to screen radiation.
It is also important to develop new spaces for simulated tests on the space environment because, nowadays, it is very difficult to perform these experiments in terrestrial conditions.
So, it may be interesting to launch more actual experiments in order to combine different aspects of the space environment and observe how materials act.
Author Contributions
F.C., M.S., and P.L. contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially supported by ATTRACT Phase2, a European Union’s Horizon 2020 RIA project (GA No. 101004462) and by the “Horizon Europe” program, funded by the European Union (C&G Kiel Italia srl -Italy, project leader. Project n. F/310234/03/X56– REA - Introduzione di mateRiali e tEcnologie circolari e sostenibili nell’industria del trasporto di massA - Introduction of circular and sustainable materials and technologies in the mass transport industry) and the European Union under the Italian National Recovery and Resilience Plan (NRRP) of NextGenerationEU, Mission 4, Component 2, Investment 1.1, Call for tender No. 1409 of 14.9.2022 of the Italian Ministry of University and Research (MUR), Project Title UPWARD CUP E53D23014490001 - Grant Assignment Decree No. 1383 of 01/09/2023.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Novoselov, K.; Geim, A.K.; Morozov, S.; Jiang, D.; Katsnelson, M.; Grigorieva, I.; Dubonos, S.V.; Firsov, A. Two-dimensional gas of massless dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Zhang, Y.; Tan, Y.W.; Stormer, H.L.; Kim, P. Quantum hall effect in graphene. Solid State Commun. 2007, 143, 14–19. [Google Scholar] [CrossRef]
- Tu, Y.; Wu, J.; Xu, G.; Yang, X.; Cai, R.; Qihuang, Q.; Zhu, R.; Huang, W. Perovskite solar cells for space applications: Progress and challenges. Adv. Mater. 2021, 33, 2006545. [Google Scholar] [CrossRef] [PubMed]
- Flynn, D.G. The Quantum Hall Effect in Graphene. 2010. Available online: https://www.physics.drexel.edu/~bob/TermPapers/Flynn_QuantumPaper.pdf (accessed on 6 March 2025).
- Parvez, K.; Li, R.; Müllen, K. Graphene as Transparent Electrodes for Solar Cells. In Nanocarbons for Advanced Energy Conversion; Feng, X., Ed.; John Wiley & Sons: New York, NY, USA, 2015; pp. 249–280. [Google Scholar]
- Goodman, K.; Aga, R.S.; Aga, R.; Cooper, R.; Cao, L.R.; Heckman, E. Investigation on electrical properties of printed graphene subjected to aging, ambient environment and gamma radiation. IEEE Trans. Device Mater. Reliab. 2023, 24, 98–104. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).