Abstract
The increase in composite material waste from the aviation and wind energy sectors will become a significant environmental challenge in the near future. This escalation is attributed to the enhanced use of new, advanced composite materials, such as Glass Fiber Reinforced Polymer (GFRP). Despite their benefits, the disposal of these materials at their end-of-life poses considerable environmental and logistical challenges. Assessing the condition of these materials is thus pivotal to develop sustainable strategies for their recycling, reusing, or repurposing. This study investigates the use of Non-Destructive Testing (NDT) techniques, with a focus on Active Thermography, to evaluate GFRP components’ suitability for sustainable management without compromising the material integrity. This research highlights the use of Active Thermography for extensive, non-invasive inspections, due to its capability to inspect a large area quickly using external energy heating. It delves into Pulse Phase Thermography (PPT) and Principal Component Thermography (PCT), two advanced signal post-processing techniques, tested on GFRP materials with purposefully induced defects. Finally, an automated method based on the Signal-to-Noise Ratio (SNR) value is implemented for defect detection, with which defects of a 5 mm diameter and a 3 mm depth can be detected. The document elaborates on the theoretical principle of NDT, PPT, and PCT, details the experimental methodology and specimens, and analyzes the outcomes of employing these techniques, drawing comparisons between them.
1. Introduction
Glass Fiber Reinforced Polymer (GFRP) is a composite material that consists of a polymer matrix and glass fibers. Due to its properties such as high strength, flexibility, or stiffness, it is a material used in different applications, including electronics, automobiles, and aviation and aerospace. However, due to fatigue and impact damage, different kinds of defects that can reduce the strength and stiffness of GFRP components, such as delamination, fiber crack, and porosity, may be induced in the GFRP laminates during its use [1].
To ensure the good condition of GFRP, Non-Destructive Testing (NDT) is usually used. NDT is a group of testing techniques used to evaluate materials and detect defects without causing damages [2]. One of the most popular NDT methods is InfraRed Thermography (IRT), based on infrared radiation. This technique is dedicated to the acquisition and processing of thermal information [3]. Inside the group of IRT, Pulsed Thermography is one of the most common active thermography testing methods; i.e., an external heat source is used to stimulate the materials under tests is required, as shown in Figure 1.
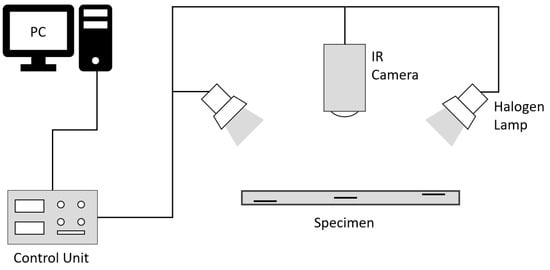
Figure 1.
Pulsed Thermography inspection system.
However, Pulsed Thermography is not perfect and has some problems such as non-uniform surface heating, lateral heat diffusion, or environmental noise. To solve these problems as much as possible, various signal post-processing techniques exist. In this paper, we particularly focus on Pulsed Phase Thermography (PPT), which is based on Discrete Fourier Transform (DFT), and Principal Components Thermography (PCT), which is based on Principal Components Analysis (PCA). To test the effectiveness of both the PPT and the PCT methods, the Signal-to-Noise Ratio (SNR) is subsequently used.
2. Active Thermography
Active Thermography is dedicated to the acquisition and processing of thermal information. Its main advantages are that it is in real time, which enables high speed scanning, and it provides two-dimensional thermal images, which allow a comparison between areas of the target [4].
Pulsed Thermography involves the use of a heat source, usually with halogen lamps, microwaves, or laser induction as a heating source [5], to stimulate an object with a heat pulse. An infrared camera records a video of the object to measure the heating and cooling process on the object’s surface, described by the following equation:
where T is the temperature function, is the initial temperature, Q is the energy on the surface, is the material’s thermal effusivity, is the material’s thermal diffusivity, k is the thermal conductivity, is the density, and is the specific heat capacity [6].
At the surface (), Equation (1) can be rewritten as
If the composite has homogeneous materials, its thermal diffusivity and conductivity are similar. However, the material of the defective area has different parameters, resulting in a distinct thermal behavior. This difference forms the theoretical basis for Pulsed Thermography.
2.1. Pulsed Phase Thermography
Initially developed by Margado and Marinetti [7,8], Pulsed Phased Thermography is a thermal image sequence post-processing method that involves the calculation of the phase of a thermal image sequence using a Discrete Fourier Transform, which is computed with the following formula:
where N is the number of thermal images, is the imaginary number, and is the sampling time interval. As a complex number, Equation (3) can be rewritten as the sum of the real () and imaginary () parts of the transform sequence:
To analyze the amplitude and the phase of every harmonic frequency Fast Fourier Transform is used as a quick algorithm of DFT. Amplitude () and phase angle () are expressed as
With phase images of DFT results, defect regions are emphasized.
2.2. Principal Components Thermography
Principal Components Analysis is a statistical technique used to identify specific patterns in large datasets containing a high number of features per observation and analyze them so as to enable the depicting of similarities and differences of specific patterns. PCA reduces the dimensionality of a dataset. This is accomplished by linearly transforming the data into a new coordinate system where the variation in the data can be described with fewer dimensions than the initial data [9,10]. The use of PCA in post-processing thermographic data is called Principal Components Thermography and was proposed by Rajic [11].
Consider the thermogram sequence as a 3D matrix composed of thermograms whose dimensions are . In order to apply PCT to the thermogram sequence, this 3D matrix is transformed into a 2D matrix of dimension by the following equivalence:
where is the element of the 3D matrix in row i, column j, and thermogram number k, and is the element of the 2D matrix in row i and column k. This 2D matrix is called a raster-like matrix. Each column of the raster-like matrix represents one thermogram of the sequence, and each row represents temperature evolution of one pixel, as shown in Figure 2.
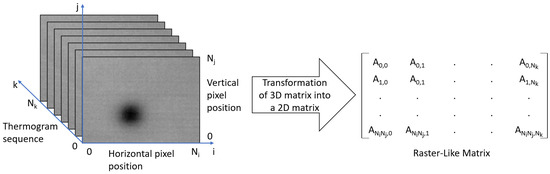
Figure 2.
Transformation of a thermogram sequence into a 2D raster-like matrix.
The raster-like matrix is decomposed with the Singular Value Decomposition, a factorization of a matrix into three matrices, by the following structure:
where U is an orthogonal matrix, V is an orthogonal matrix, and S is an diagonal matrix with its elements uniquely determined by the singular values of A sorted from highest to lowest.
In the described factorization, the columns of the matrix U represent a set of orthogonal statistical models known as the Empirical Orthogonal Functions, . If images are depicted, each corresponds to the respective most characteristic data variability, i.e., is the first most characteristic data variability, is the second, etc. In , a distribution is obtained that characterizes a non-uniform field where spatial distribution can be correlated with a contrast signal, which occurs due to the defect in the sample. Therefore, of PCT gives an image that characterizes the defects embedded in the observed sample [12].
3. Signal-to-Noise Ratio
Before the post-processing techniques, the Signal-to-Noise Ratio [13] measure is applied for the automatic detection of defects.
SNR is a measure that compares the level of a desired signal to the level of background noise. SNR is used to refer to the ratio of useful information to irrelevant data and is defined by the following equation:
where S is the average value of the signal area, N is the average value of the noise area, and is the standard deviation of the noise area.
In respect to the quantitative evaluation, a defect is detected if dB, but it must be noted that defects are more clearly identified if the SNR value is greater.
For the automatic detection, we select a quadrant as the signal area, and a quadrant with the signal area in the center as the noise area. We move pixel by pixel the two areas until the entire image is filled, as in Figure 3a. When more than 4 signal areas with intersect with each other, we regroup them in a larger quadrant and take this as a defect, with the higher SNR of the little quadrants taken as the SNR, as in Figure 3b.

Figure 3.
Automatic defect detection. (a) Selection of noise and signal areas. (b) Defect detection.
4. Data Information
4.1. Calibration Plate
For the purpose of comparing the different post-processing techniques, they have been applied to a real GFRP piece with artificial defects. In Figure 4a, the test piece is shown. In Figure 4b, the map of the defects can be seen.
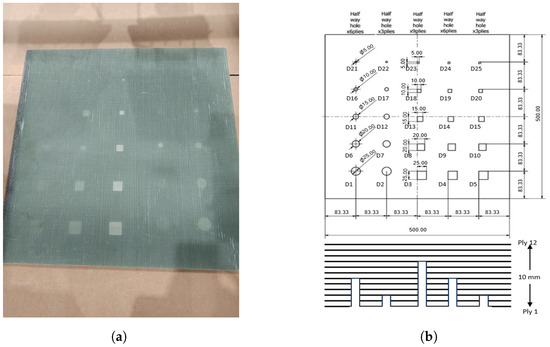
Figure 4.
Subject of study. (a) Photo of the specimen. (b) Map of the defects.
The specimen is made of 12 plies of glass-fiber filled with epoxy. Each ply has a depth of 0.83 mm and is numbered from 1 to 12, where Ply 12 is the closest to the surface in which the temperature is measured. The total thickness of the piece is 10 mm. In the specimen, 25 numbered half way hole defects exist; 10 of them are circular in shape, and the rest of them are square-shaped. All defects are found at three different depths: 2.5 mm, 5 mm, and 7.5 mm. In Figure 4a, it can be seen that some defects are observable to the naked eye due to the proximity of the half way holes to the surface.
4.2. Setup
In the experiment, four halogen lamps, two of them of 1000 watts at a distance from each other of 70 cm and the other two of 500 watts at a distance from each other of 50 cm, were used as the heat source. The lamps were turned on for 60 s to heat the specimen. Then, the lamps were turned off and the temperature decay was recorded for another 60 s.
The experiment was recorded using an InfraTec VarioCAM® HD Head 800 [14]. The spectral range of this camera is between 7.5 and 14 µm and has a temperature measure range between −40 and 2000 °C. The resolution of the camera is of (1024 × 768) pixels. Though the camera is able to record with a frame rate of 240 Hz, the experiment was recorded at 30 Hz to reduce the number of acquired images. The distance between the camera and the piece of GFRP was 100 cm.
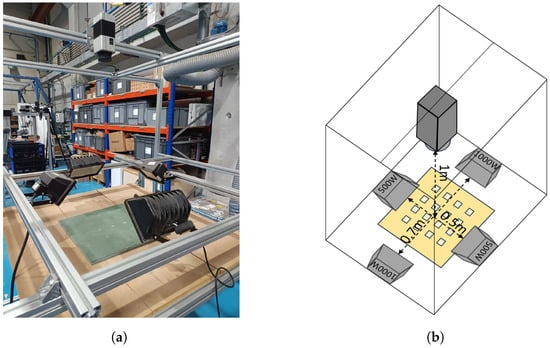
Figure 5.
Subject of study. (a) Photo of the setup. (b) Schema of the setup.
For both image capture and subsequent post-precessing with PPT and PCT, we used the Thermogarphy and Ultrasound Testing Tool (TUTT) available at zenodo.org [15] and developed under the same project as this article.
5. Results and Discussion
The images resulting from the application of PPT and PCT can be seen in Figure 6 and Figure 7, respectively.
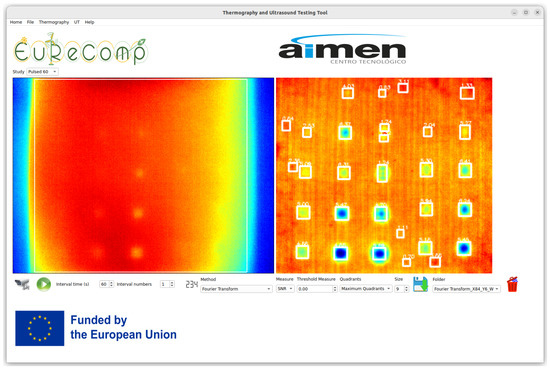
Figure 6.
GFRP plate inspected with PPT. On the left of the figure, the first thermal image and the RoI are selected. On the right, the resulting image using PPT is shown.
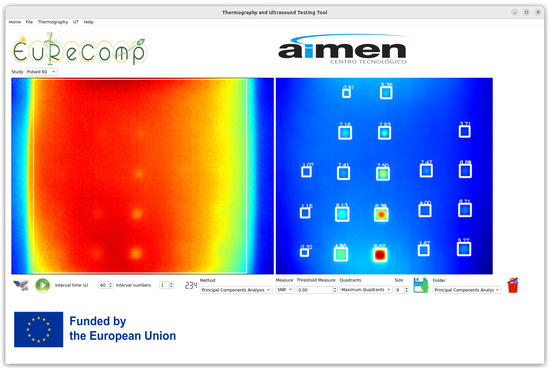
Figure 7.
GFRP plate inspected with PCT. On left of the figure, the first thermal image and the RoI selected. On right, the result image using PCT.
In Table 1, True Positives (TP), False Positives (FP), and False Negatives (FN) are specified for both Active Thermography techniques. The PPT method achieves a precision () of and a recall () of . The PCT method achieves a precision of 1 and a recall of .

Table 1.
Precision and Recall for methods PPT and PCT.
On the other hand, in Table 2, the SNR for all defects can be seen.

Table 2.
SNR value for each defect for methods PPT and PCT. Detections are in green, and non-detections are in red.
Comparing both techniques, in other tests, it can be seen that, while PPT obtains a better recall, i.e., it effectively detects more defects, PCT obtains a better precision, i.e., it detects fewer fake defects in proportion with the total real defects.
6. Conclusions and Future Works
In this work, pulsed thermography was applied to a GFRP calibration plate with the aim to detect half hole defects. The concepts of PPT and PCT have been reviewed for the processing and analysis of thermal images. Each signal processing technique was evaluated by the automatic use of SNR. Based on the results, it was determined that the automatic use of SNR is highly effective when defects are larger than 5 mm in diameter. However, when defects are less than 5 mm in diameter and less than 2.5 mm deep, the method should be improved.
Comparing PPT and PCT, it could be observed that PPT performs better in finding smaller and deeper defects, while PCT provides a higher SNR on larger defects closer to the surface. On the other hand, PPT tends to make more errors in detection than PCT, thus obtaining a higher precision for the latter method.
Future work will focus on applying these methods in real scenarios, such as the inspection of a wind turbine blade, and improving their implementation.
Author Contributions
Conceptualization, M.G. and D.C.; methodology, M.G. and D.C.; software, M.G.; validation, D.C.; formal analysis, M.G.; investigation, M.G. and D.C.; resources, M.G.; data curation, M.G. and D.C.; writing—original draft preparation, M.G.; writing—review and editing, D.C.; supervision, D.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been developed within the EURECOMP project under the grant agreement 101058089, funded by the European Union. Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or HADEA. Neither the European Union nor HADEA can be held responsible for them.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This work was supported by AIMEN Centro Tecnológico under Project EuReComp.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GFRP | Glass Fiber Reinforced Polymer |
| NDT | Non-Destructive Testing |
| PPT | Pulsed Phase Thermography |
| PCT | Principal Components Thermography |
| SNR | Signal to Noise Ratio |
| IRT | InfrRed Thermography |
| DFT | Discrete Fourier Transform |
| PCA | Principal Components Analysis |
| EOF | Empirical Orthogonal Functions |
References
- Sathishkumar, T.; Satheeshkumar, S.; Naveen, J. Glass fiber-reinforced polymer composites—A review. J. Reinf. Plast. Compos. 2014, 33, 1258–1275. [Google Scholar] [CrossRef]
- Chen, J.; Yu, Z.; Jin, H. Nondestructive testing and evaluation techniques of defects in fiber-reinforced polymer composites: A review. Front. Mater. 2022, 9, 986645. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Venegas, P.; Guerediaga, J.; Vega, L.; Molleda, J.; Bulnes, F.G. Infrared Thermography for Temperature Measurement and Non-Destructive Testing. Sensors 2014, 14, 12305–12348. [Google Scholar] [CrossRef] [PubMed]
- Parker, W.; Jenkins, R.; Butler, C.; Abbott, G. Flash method of determining thermal diffusivity, heat capacity, and thermal conductivity. J. Appl. Phys. 1961, 32, 1679–1684. [Google Scholar] [CrossRef]
- Wang, R.; Pei, C.; Xia, R.; Wang, Q.; Chen, Z. A portable fiber laser thermography system with beam homogenizing for CFRP inspection. NDT E Int. 2021, 124, 102550. [Google Scholar] [CrossRef]
- Chung, Y.; Lee, S.; Kim, W. Latest advances in common signal processing of pulsed thermography for enhanced detectability: A review. Appl. Sci. 2021, 11, 12168. [Google Scholar] [CrossRef]
- Maldague, X. Theory and Practice of Infrared Technology for Nondestructive Testing; Wiley-Interscience: Hoboken, NJ, USA, 2001. [Google Scholar]
- Maldague, X.; Galmiche, F.; Ziadi, A. Advances in pulsed phase thermography. Infrared Phys. Technol. 2002, 43, 175–181. [Google Scholar] [CrossRef]
- Pearson, K. Principal components analysis. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 6, 559. [Google Scholar] [CrossRef]
- Daultrey, S. Principal Components Analysis; Geo Abstracts Limited: Norwich, UK, 1976; Volume 8. [Google Scholar]
- Rajic, N. Principal component thermography for flaw contrast enhancement and flaw depth characterisation in composite structures. Compos. Struct. 2002, 58, 521–528. [Google Scholar] [CrossRef]
- Milovanović, B.; Gaši, M.; Gumbarević, S. Principal component thermography for defect detection in concrete. Sensors 2020, 20, 3891. [Google Scholar] [CrossRef] [PubMed]
- Gragido, W.; Pirc, J.; Selby, N.; Molina, D. Chapter 4—Signal-to-Noise Ratio. In Blackhatonomics; Gragido, W., Pirc, J., Selby, N., Molina, D., Eds.; Syngress: Boston, MA, USA, 2013; pp. 45–55. [Google Scholar] [CrossRef]
- InfraTec GmbH Infrarotsensorik und Messtechnik. InfraRed Camera VarioCAM HD Head 800. Available online: https://www.infratec.eu/thermography/infrared-camera/variocam-hd-head-800/ (accessed on 28 October 2024).
- Asociación de Investigación Metalúrgica del Noroeste; Fernández, M.G.; Boga, D.C. Thermography and Ultrasound Testing Tool. 2024. Available online: https://doi.org/10.5281/zenodo.13833956 (accessed on 28 October 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).