Visual Navigation for Lunar Missions Using Sequential Triangulation Technique †
Abstract
1. Introduction
2. Problem Statement
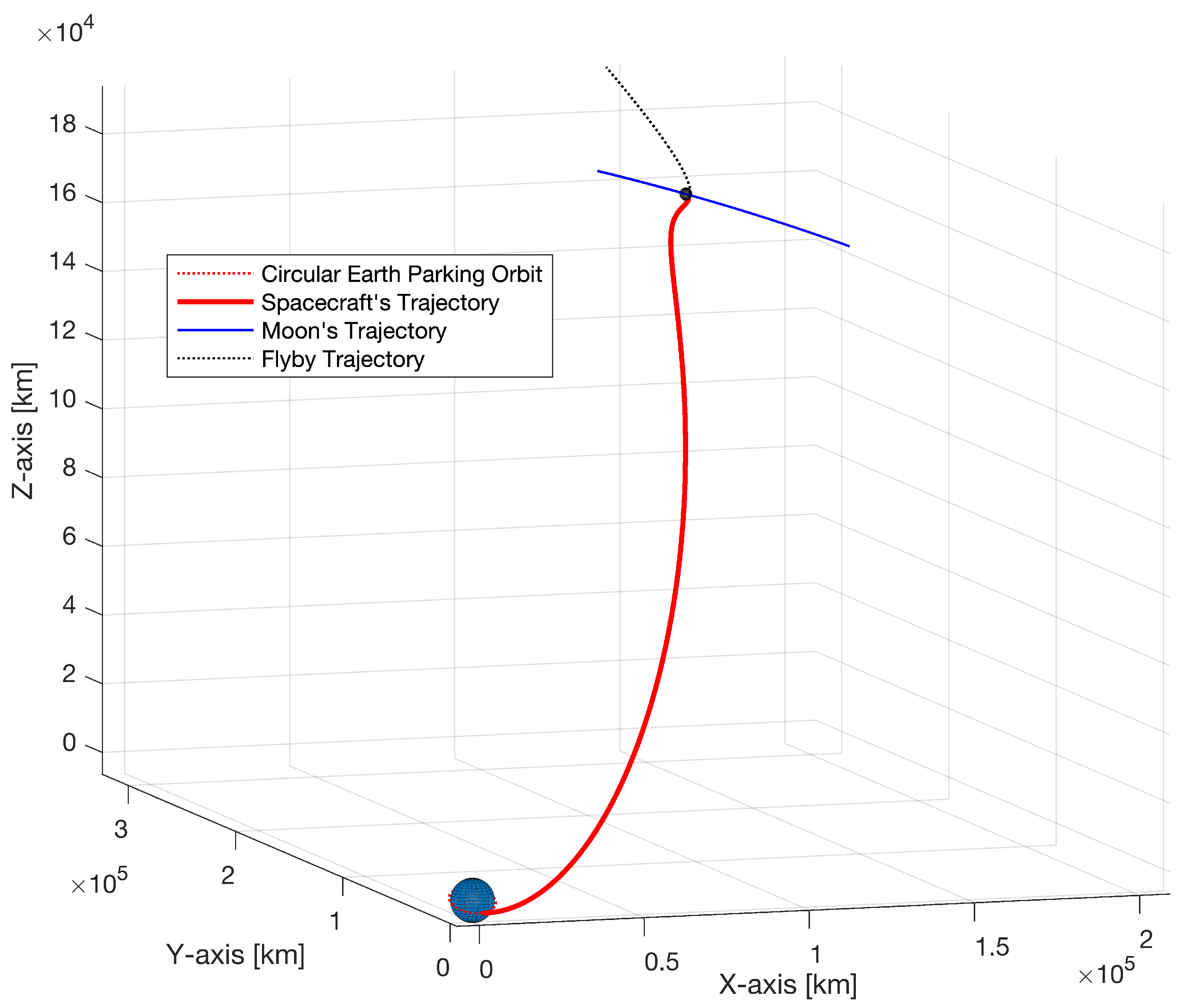
3. Simulation Model
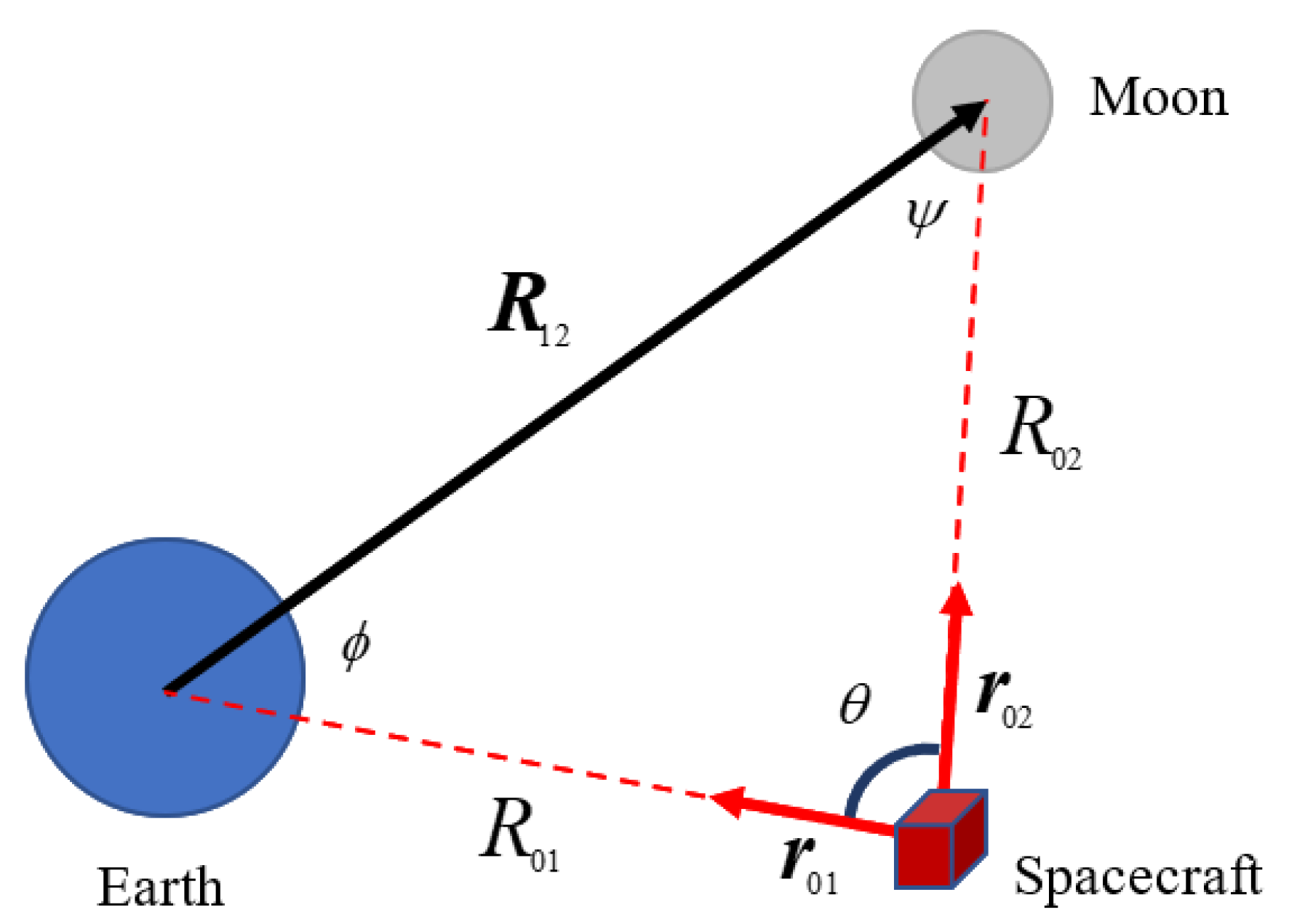
4. Triangulation and Error Model
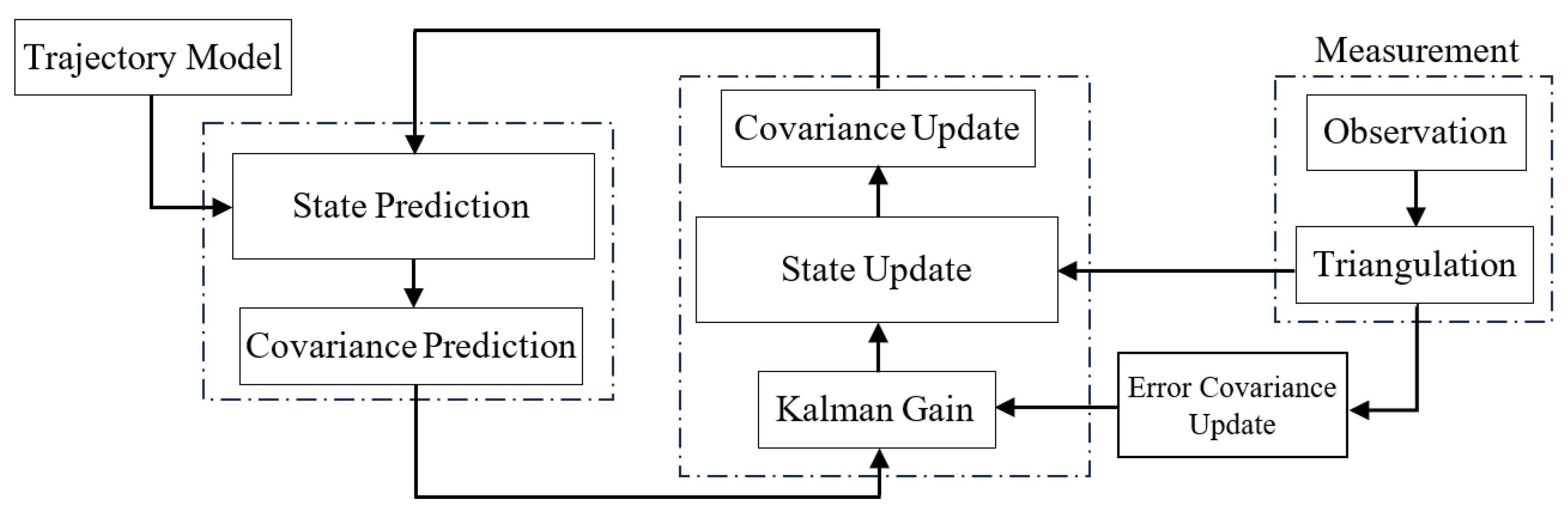
5. Extended Kalman Filter
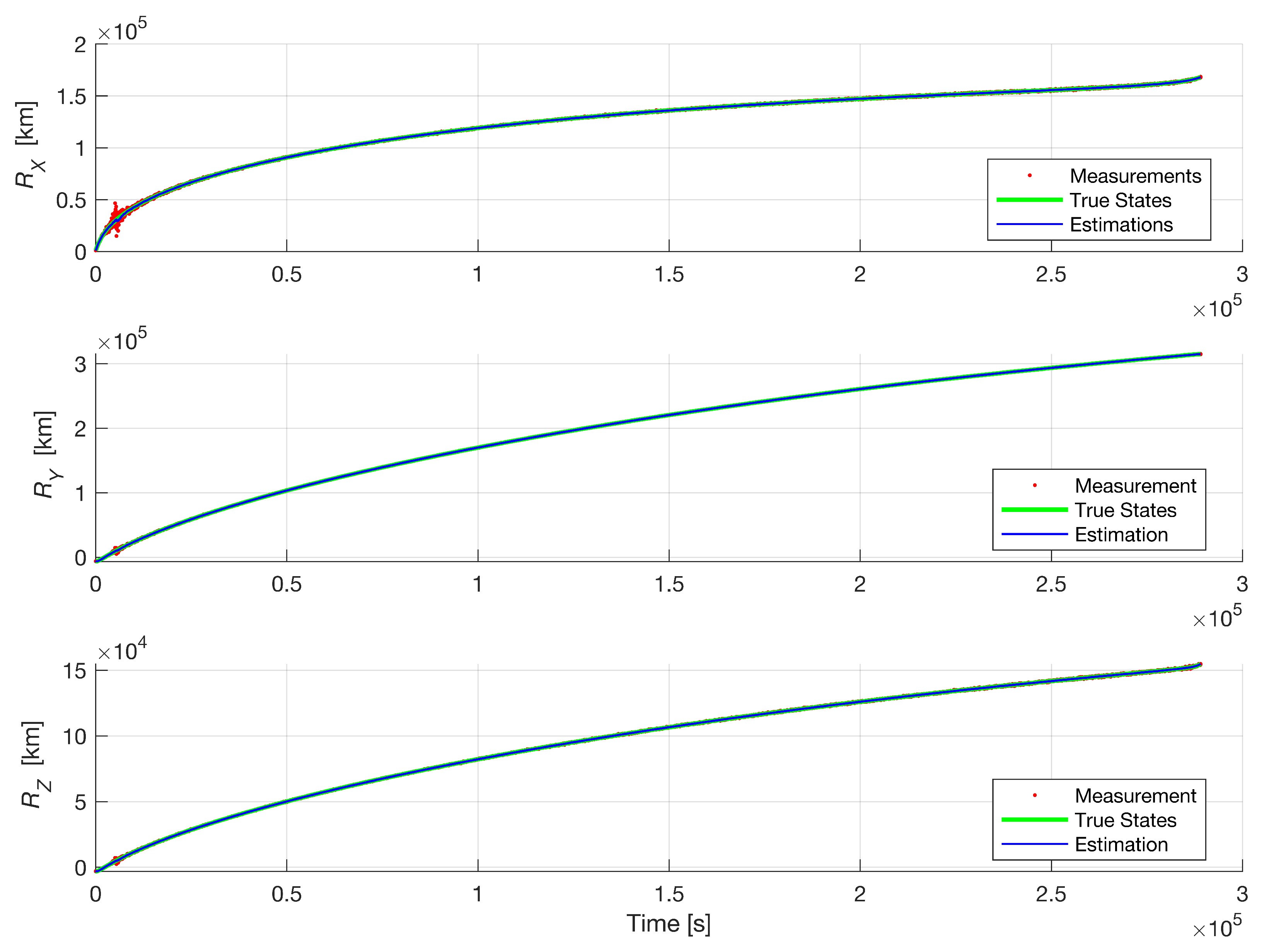
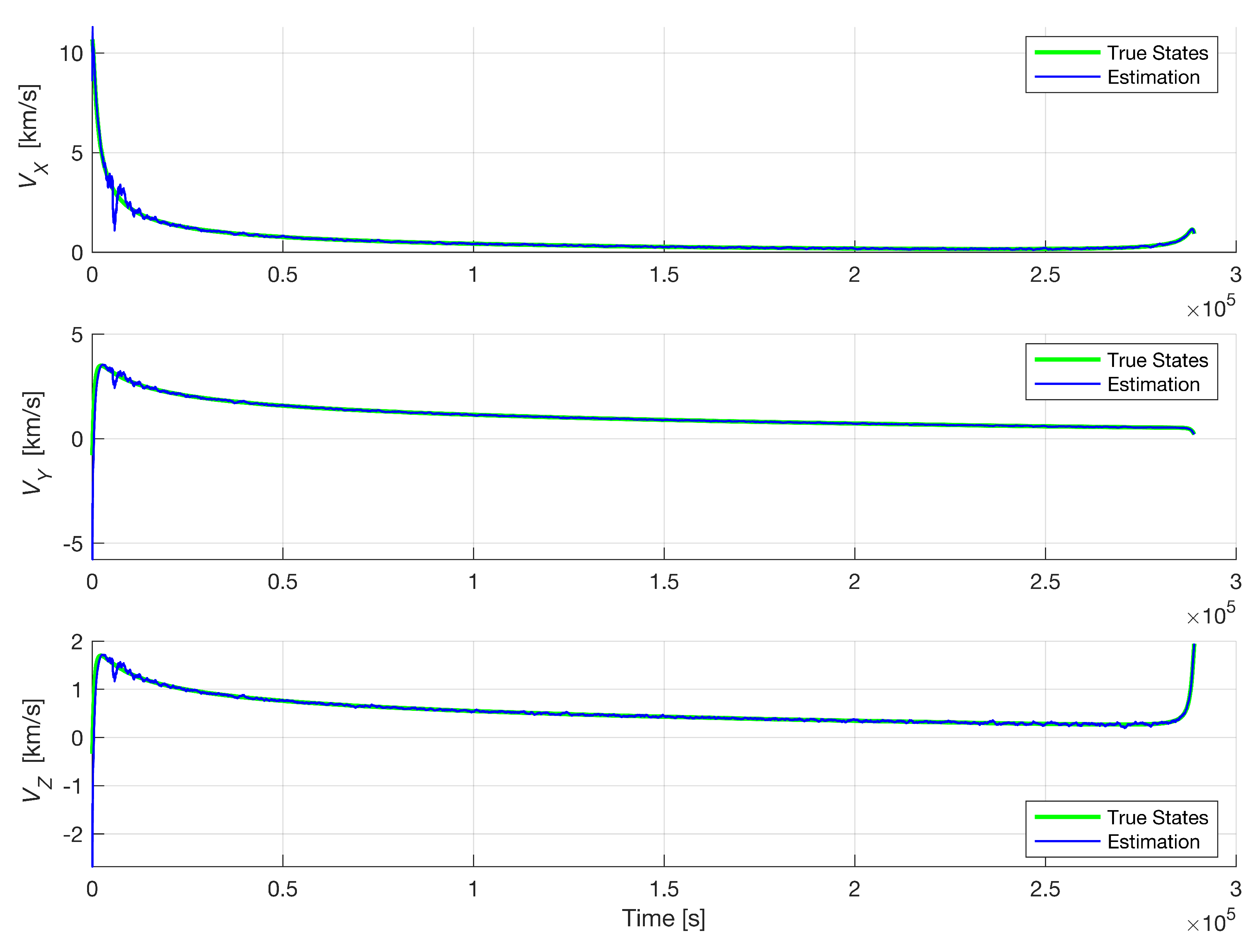
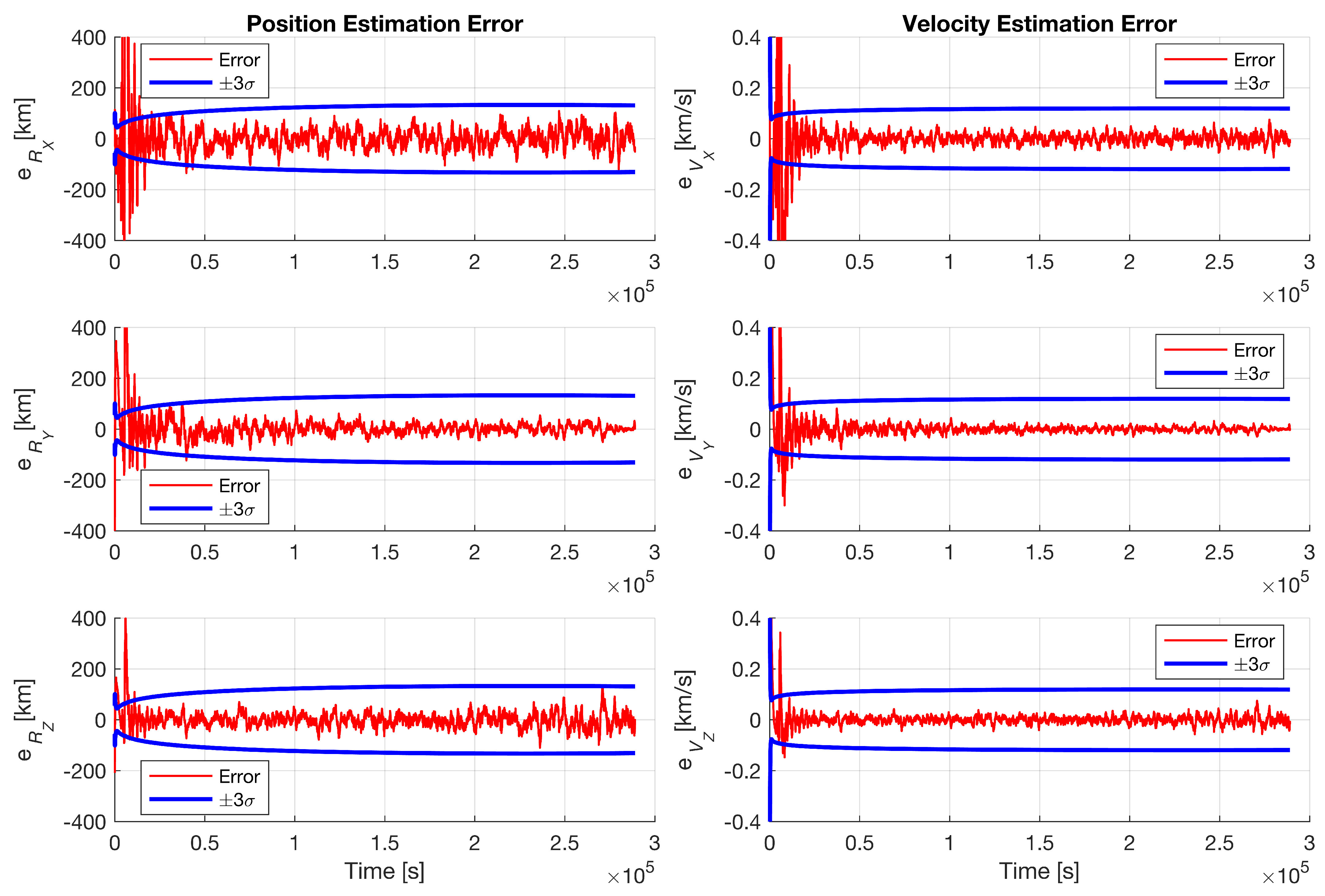
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yüksel, M.; Roehr, T.M.; Jankovic, M.; Brinkmann, W.; Kirchner, F. A reference implementation for knowledge assisted robot development for planetary and orbital robotics. Acta Astronaut. 2023, 210, 197–211. [Google Scholar] [CrossRef]
- Trawny, N.; Mourikis, A.I.; Roumeliotis, S.I.; Johnson, A.E.; Montgomery, J.F. Vision-aided inertial navigation for pin-point landing using observations of mapped landmarks. J. Field Robot. 2007, 24, 357–378. [Google Scholar] [CrossRef]
- Cui, P.; Gao, X.; Zhu, S.; Shao, W. Visual navigation based on curve matching for planetary landing in unknown environments. Acta Astronaut. 2020, 170, 261–274. [Google Scholar] [CrossRef]
- Hesch, J.A.; Kottas, D.G.; Bowman, S.L.; Roumeliotis, S.I. Consistency analysis and improvement of vision-aided inertial navigation. IEEE Trans. Robot. 2013, 30, 158–176. [Google Scholar] [CrossRef]
- Christian, J.A. A tutorial on horizon-based optical navigation and attitude determination with space imaging systems. IEEE Access 2021, 9, 19819–19853. [Google Scholar] [CrossRef]
- Cassinis, L.P.; Fonod, R.; Gill, E. Review of the robustness and applicability of monocular pose estimation systems for relative navigation with an uncooperative spacecraft. Prog. Aerosp. Sci. 2019, 110, 100548. [Google Scholar] [CrossRef]
- Johnson, A.E.; Montgomery, J.F. Overview of terrain relative navigation approaches for precise lunar landing. In Proceedings of the 2008 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–10. [Google Scholar]
- Cocaud, C.; Kubota, T. SLAM-based navigation scheme for pinpoint landing on small celestial body. Adv. Robot. 2012, 26, 1747–1770. [Google Scholar] [CrossRef]
- Christian, J.A.; Hong, L.; McKee, P.; Christensen, R.; Crain, T.P. Image-based lunar terrain relative navigation without a map: Measurements. J. Spacecr. Rocket. 2021, 58, 164–181. [Google Scholar] [CrossRef]
- Maass, B.; Woicke, S.; Oliveira, W.M.; Razgus, B.; Krüger, H. Crater navigation system for autonomous precision landing on the moon. J. Guid. Control. Dyn. 2020, 43, 1414–1431. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, J. Crater detection and recognition method for pose estimation. Remote Sens. 2021, 13, 3467. [Google Scholar] [CrossRef]
- Johnson, A.; Aaron, S.; Chang, J.; Cheng, Y.; Montgomery, J.; Mohan, S.; Schroeder, S.; Tweddle, B.; Trawny, N.; Zheng, J. The lander vision system for mars 2020 entry descent and landing. Guid. Navig. Control 2017, 2017, 159. [Google Scholar]
- Johnson, A.E.; Cheng, Y.; Trawny, N.; Montgomery, J.F.; Schroeder, S.; Chang, J.; Clouse, D.; Aaron, S.; Mohan, S. Implementation of a Map Relative Localization System for Planetary Landing. J. Guid. Control. Dyn. 2023, 46, 618–637. [Google Scholar]
- Rebordão, J. Space optical navigation techniques: An overview. In Proceedings of the 8th Iberoamerican Optics Meeting and 11th Latin American Meeting on Optics, Lasers, and Applications, Porto, Portugal, 22–26 July 2013; SPIE: Bellingham, WA, USA, 2013; Volume 8785, pp. 29–48. [Google Scholar]
- Christian, J.A. Accurate planetary limb localization for image-based spacecraft navigation. J. Spacecr. Rocket. 2017, 54, 708–730. [Google Scholar]
- Adams, V.H.; Peck, M.A. Interplanetary optical navigation. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Adams, V.H.; Peck, M.A. Lost in space and time. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Franzese, V.; Di Lizia, P.; Topputo, F. Autonomous optical navigation for lumio mission. In Proceedings of the 2018 Space Flight Mechanics Meeting, Kissimmee, FL, USA, 8–12 January 2018; AIAA: Reston, VA, USA, 2018; p. 1977. [Google Scholar]
- Franzese, V.; Di Lizia, P.; Topputo, F. Autonomous optical navigation for the lunar meteoroid impacts observer. J. Guid. Control. Dyn. 2019, 42, 1579–1586. [Google Scholar]
- Li, C.; Zheng, Y.; Li, Z.; Yu, L.; Wang, Y. A New Celestial Positioning Model Based on Robust Estimation. In Proceedings of the China Satellite Navigation Conference (CSNC) 2013 Proceedings, Wuhan, China, 15–17 May 2013; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2013; Volume 245, pp. 479–487. [Google Scholar]
- Raymond Karimi, R.; Mortari, D. Interplanetary autonomous navigation using visible planets. J. Guid. Control. Dyn. 2015, 38, 1151–1156. [Google Scholar]
- Broschart, S.B.; Bradley, N.; Bhaskaran, S. Kinematic approximation of position accuracy achieved using optical observations of distant asteroids. J. Spacecr. Rocket. 2019, 56, 1383–1392. [Google Scholar]
- Henry, S.; Christian, J.A. Absolute triangulation algorithms for space exploration. J. Guid. Control. Dyn. 2023, 46, 21–46. [Google Scholar]
- Chen, X.; Sun, Z.; Zhang, W.; Xu, J. A novel autonomous celestial integrated navigation for deep space exploration based on angle and stellar spectra shift velocity measurement. Sensors 2019, 19, 2555. [Google Scholar] [CrossRef]
- Christian, J.A. StarNAV: Autonomous optical navigation of a spacecraft by the relativistic perturbation of starlight. Sensors 2019, 19, 4064. [Google Scholar] [CrossRef]
- Shuster, M.D.; Oh, S.D. Three-axis attitude determination from vector observations. J. Guid. Control 1981, 4, 70–77. [Google Scholar]
- Chiaradia, A.P.M.; Kuga, H.K.; Prado, A.F.B.d.A. Onboard and Real-Time Artificial Satellite Orbit Determination Using GPS. Math. Probl. Eng. 2013, 2013, 530516. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muratoglu, A.; Söken, H.E.; Tekinalp, O. Visual Navigation for Lunar Missions Using Sequential Triangulation Technique. Eng. Proc. 2025, 90, 27. https://doi.org/10.3390/engproc2025090027
Muratoglu A, Söken HE, Tekinalp O. Visual Navigation for Lunar Missions Using Sequential Triangulation Technique. Engineering Proceedings. 2025; 90(1):27. https://doi.org/10.3390/engproc2025090027
Chicago/Turabian StyleMuratoglu, Abdurrahim, Halil Ersin Söken, and Ozan Tekinalp. 2025. "Visual Navigation for Lunar Missions Using Sequential Triangulation Technique" Engineering Proceedings 90, no. 1: 27. https://doi.org/10.3390/engproc2025090027
APA StyleMuratoglu, A., Söken, H. E., & Tekinalp, O. (2025). Visual Navigation for Lunar Missions Using Sequential Triangulation Technique. Engineering Proceedings, 90(1), 27. https://doi.org/10.3390/engproc2025090027





