Validity of the Shear Panel Theory as a Reduced Modelling Approach †
Abstract
1. Introduction
2. Materials and Methods
2.1. Shear Panel Theory—Assumptions and Analytical Solutions
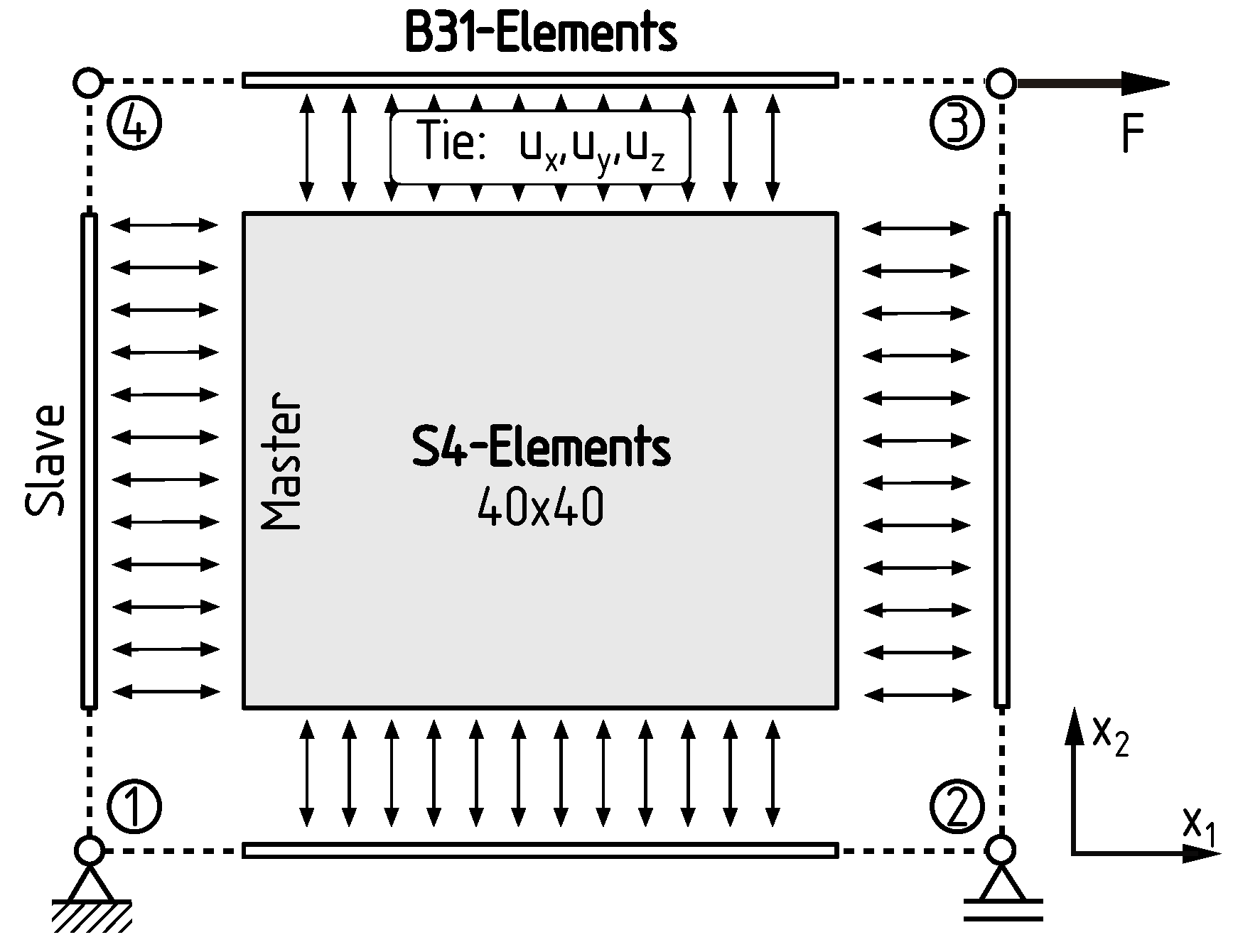
2.2. FEM Reference Model
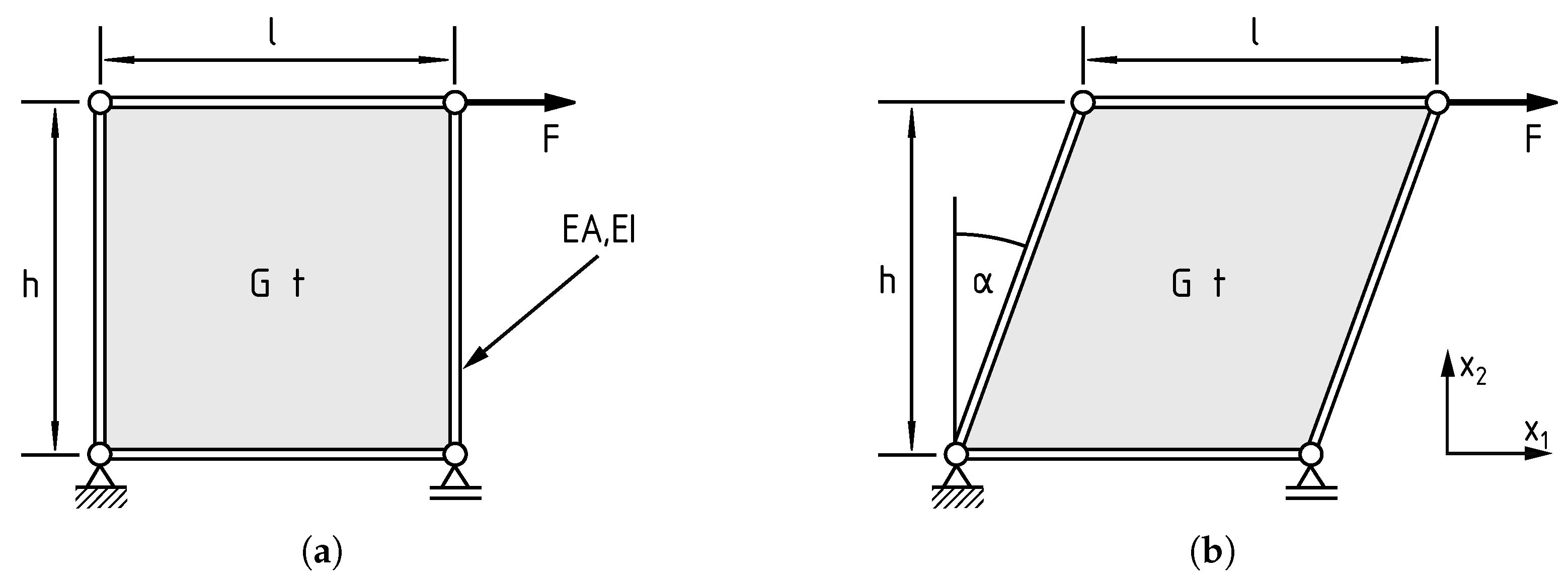
2.3. Definition of Parameter Study for the Rectangular and Parallelogram Panel
3. Results
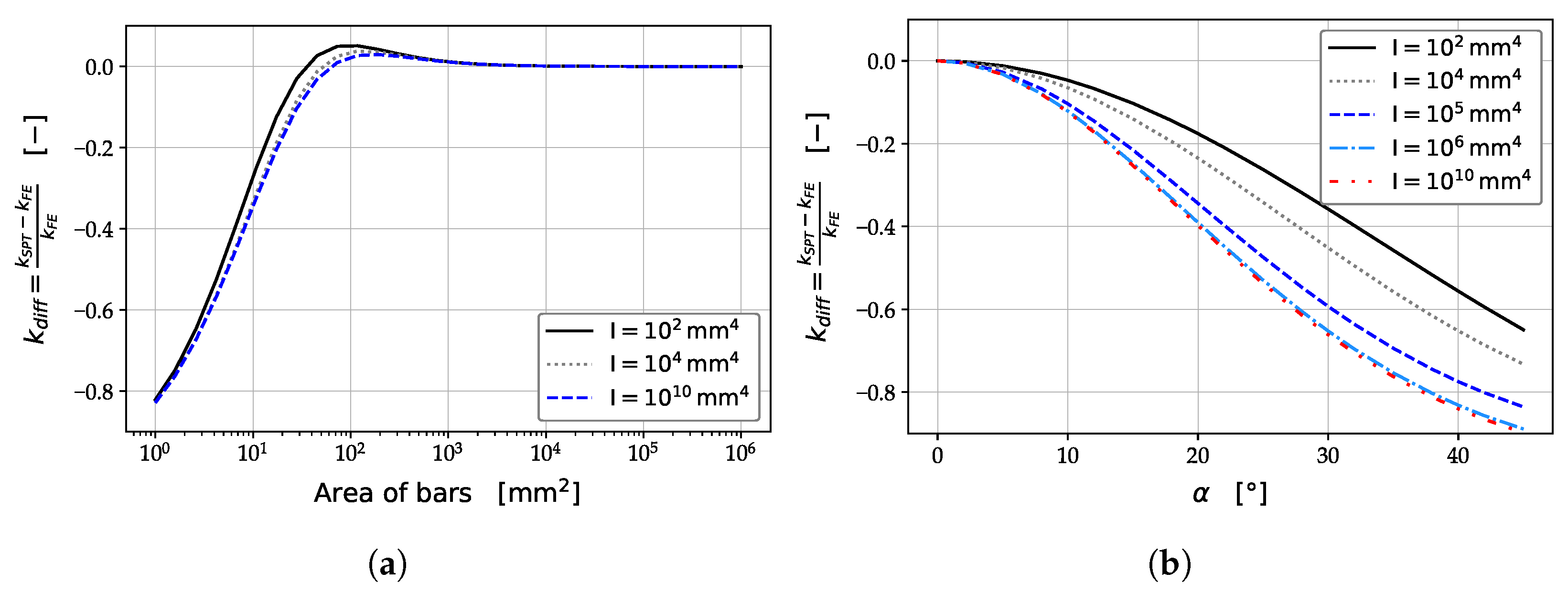
3.1. Parameter Study: Rectangular Shear Panel
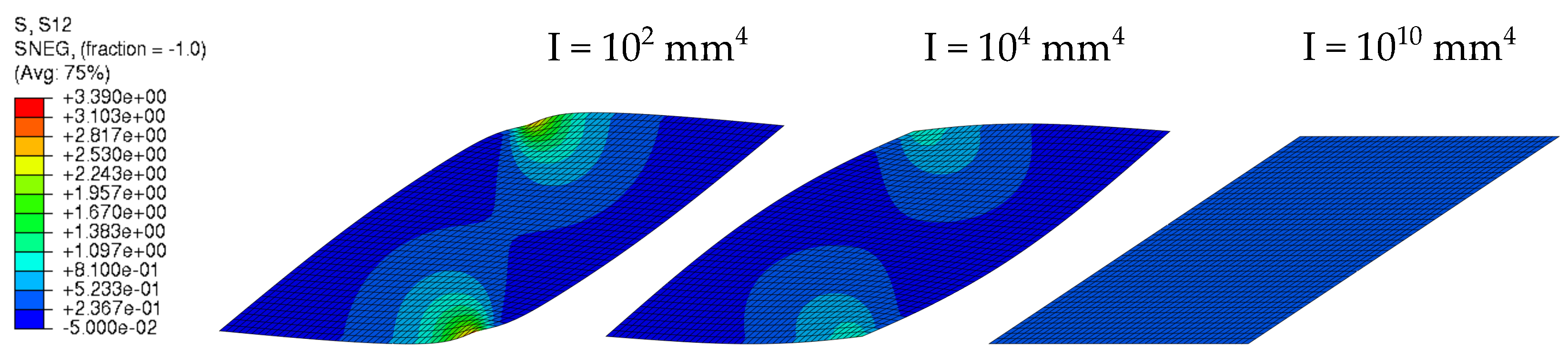
3.2. Parameter Study: Parallelogram Shear Panel
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| SPT | Shear Panel Theory |
References
- Parolin, G.; Borges, A.T.; Santos, L.C.; Borille, A.V. A tool for aircraft eco-design based on streamlined Life Cycle Assessment and Uncertainty Analysis. Procedia CIRP 2021, 98, 565–570. [Google Scholar] [CrossRef]
- Lyssakow, P.; Krause, M.; Friedrich, L.; Schröder, K.-U. Towards a coupled structural and economical design procedure of unstiffened isotropic shell structures. Thin-Walled Struct. 2019, 145, 106416. [Google Scholar] [CrossRef]
- Lyssakow, P.; Yang, J.; Krause, M.; Schröder, K.-U. Analysis of mass and cost drivers of unstiffened isotropic shell structures considering their imperfection sensitivity. Thin-Walled Struct. 2021, 159, 107221. [Google Scholar] [CrossRef]
- Quatmann, M.; Reimerdes, H.-G. Preliminary design of composite fuselage structures using analytical rapid sizing methods. CEAS Aeronaut. J. 2011, 2, 231–241. [Google Scholar] [CrossRef]
- Mittelstedt, C.; Schröder, K.-U. Local postbuckling of hat-stringer-stiffened composite laminated plates under transverse compression. Compos. Struct. 2010, 92, 2830–2844. [Google Scholar] [CrossRef]
- Mittelstedt, C.; Erdmann, H.; Schröder, K.-U. Postbuckling of imperfect rectangular composite plates under inplane shear closed-form approximate solutions. Arch. Appl. Mech. 2011, 81, 1409–1426. [Google Scholar] [CrossRef]
- Krause, M.; Lyssakow, P.; Friedrich, L.; Schröder, K.-U. Panel buckling of stiffened shell structures with torsional stiff stringer. Aerosp. Sci. Technol. 2020, 107, 106257. [Google Scholar] [CrossRef]
- Krause, M.; Lyssakow, P.; Schröder, K.-U. Improved approach for the panel buckling calculation of stiffened shell structures with torsional stiff stringer. Thin-Walled Struct. 2022, 171, 108829. [Google Scholar] [CrossRef]
- Krause, M.; Lyssakow, P.; Schröder, K.-U. Minimum stiffness criterion for ring frames of stringer frame stiffened shell structures. Thin-Walled Struct. 2023, 182, 110155. [Google Scholar] [CrossRef]
- Grihon, S.; Krog, L.; Bassir, D. Numerical Optimization applied to structure sizing at AIRBUS: A multi-step process. Int. J. Simul. Multidisci. Des. Optim. 2009, 3, 432–442. [Google Scholar] [CrossRef]
- Richstein, R.; Schröder, K.-U. Characterizing the Digital Twin in Structural Mechanics. Designs 2024, 8, 8. [Google Scholar] [CrossRef]
- Wiedemann, J. Leichtbau: Elemente und Konstruktion, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- VDI 2221—Part 1 (2019), Design of Technical Products and Systems—Model of Product Design; Verein Deutscher Ingenieure: Harzgerode, Germany, 2019.
- Kurrer, K.-E. The History of the Theory of Structures: From Arch Analysis to Computational Mechanics; Ernst: Berlin, Germany, 2008; ISBN 3433018383. [Google Scholar]
- Hoogenboom, P.C.J.; Blaauwendraad, J. Quadrilateral shear panel. Eng. Struct. 2000, 22, 1690–1698. [Google Scholar] [CrossRef]
- Curtis, H.D.; Greiner, G.P. A stress-based quadrilateral shear panel. Finite Elem. Anal. Des. 1996, 21, 159–178. [Google Scholar] [CrossRef]
- Chen, H.C. A simple quadrilateral shear panel element. Commun. Appl. Numer. Methods 1992, 8, 1–7. [Google Scholar] [CrossRef]
- Garvey, S.J. The Quadrilateral ‘Shear’ Panel: The Peculiar Stressing Problems Arising in the Structure of the Non-Rectangular Swept Wing. Aircr. Eng. Aerosp. Technol. 1951, 23, 134–144. [Google Scholar] [CrossRef]
- Mittelstedt, C. Structural Mechanics in Lightweight Engineering; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Dieker, S.; Reimerdes, H.G. Elementare Festigkeitslehre im Leichtbau; Donat Verlag: Bremen, Germany, 1992; ISBN 3924444587. [Google Scholar]
- Wagner, H. Ebene Blechwandträger mit sehr dünnem Stegblech. Zeitschrift für Flugtechnik und Motorluftschiffahrt 1929, 20, 200–207, 227–233, 256–262, 279–284, 306–314. [Google Scholar]
- Kuhn, P.; Peterson, J.P.; Levin, L.R. A Summary of Diagonal Tension–Part I: Methods and Analysis; NACA TN 2661; NASA: Washington, DC, USA, 1952.



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bäß, M.; Schröder, K.-U. Validity of the Shear Panel Theory as a Reduced Modelling Approach. Eng. Proc. 2025, 90, 23. https://doi.org/10.3390/engproc2025090023
Bäß M, Schröder K-U. Validity of the Shear Panel Theory as a Reduced Modelling Approach. Engineering Proceedings. 2025; 90(1):23. https://doi.org/10.3390/engproc2025090023
Chicago/Turabian StyleBäß, Moritz, and Kai-Uwe Schröder. 2025. "Validity of the Shear Panel Theory as a Reduced Modelling Approach" Engineering Proceedings 90, no. 1: 23. https://doi.org/10.3390/engproc2025090023
APA StyleBäß, M., & Schröder, K.-U. (2025). Validity of the Shear Panel Theory as a Reduced Modelling Approach. Engineering Proceedings, 90(1), 23. https://doi.org/10.3390/engproc2025090023





