Early Detection of Coherent GNSS Spoofing Attacks with Cluster Analysis at Receiver Acquisition Stage ^†

Abstract

The resilience of Global Navigation Satellite System (GNSS) usage against spoofing attacks can be increased by signal monitoring algorithms aiming to detect a spoofing signal at the acquisition stage of GNSS receiver signal processing. A common approach is to search for the presence of multiple correlation peaks in the absolute value of the Cross-Ambiguity Function (CAF). In this context, it is particularly challenging to detect spoofing signals with a correlation peak closely aligned to that of the authentic signal, as is the case at the early stage of a coherent spoofing attack. In the present work, a spoofing detection method is proposed that monitors the magnitude of the CAF by means of clustering techniques. It is designed to detect the pull-off during a coherent power-matched spoofing attack already at an early stage. The method is evaluated for the GPS L1 C/A signal based on a static scenario from the Texas Spoofing Test Battery (TEXBAT) data set as well as for the Galileo E1-B signal based on a real-world digital snapshot recording in the E1 frequency band that is augmented by emulated spoofing signals at the level of digital signal processing.

1. Introduction

The integrity and quality of Global Navigation Satellite System (GNSS) signals can be severely impaired by radio frequency interference (RFI) such as spoofing, i.e., the transmission of counterfeited GNSS signals intended to induce a deliberate false position, velocity and timing (PVT) output of a GNSS receiver. Open service GNSS signals are also widely used for critical applications like energy grid monitoring or telecommunications [1] and they are particularly vulnerable to spoofing attacks due to their publicly documented signal structure [2,3]. Therefore, all the more important are methods for timely and easily feasible spoofing detection. With respect to this, receiver-autonomous signal-processing oriented techniques [4] are appealing since they do not need additional specialized hardware such as array antennas, for example. Within the aforesaid category, monitoring of the Cross-Ambiguity Function (CAF) is frequently envisaged, e.g., in [5,6]. As pointed out there, this approach is challenging in situations when the code phase and Doppler shift of the spoofing signal agree quite well with the respective signal parameters of the authentic signal. This is the case at the early stage of a coherent, power-matched spoofing attack, which would be a favorable choice for an attacker in order to remain undiscovered.

In the present paper, an algorithm is proposed and evaluated that aims to detect attacks of the latter type already at an early stage. Then, disturbances of a single, authentic correlation peak in the CAF and the beginning of the formation of additional peaks appear as early symptoms of the starting pull-off of the spoofing signal from the authentic one. An appropriate clustering technique is applied to particularly preprocessed CAF data, which enables timely automatized recognition of these early symptoms.

The remainder of this paper is organized as follows. Section 2 gives an overview of the applied GNSS signal processing that yields the CAF and related data as input for the proposed spoofing detection algorithm. Moreover, the algorithm itself is presented there. The data sets used for a first evaluation of the spoofing detection performance of the algorithm are described in Section 3, followed by the evaluation itself in Section 4 and concluding remarks in Section 5.

2. Methodology

2.1. GNSS Signal Processing

2.1.1. GNSS Receiver Front-End

In the GNSS receiver front-end, preprocessing of the received radio frequency (RF) signal is performed. This yields an analog-to-digital (AD) converted discrete signal $r\left(m\Delta t\right),$ where $m\Delta t$ is the sampling time associated with the temporal increment $\Delta t=1/f_S$ stemming from the sampling frequency $f_S$ and $m\in {\mathbb{N}}_0$ enumerates the sampling step. Besides amplification, band pass filtering and down-conversion to an intermediate frequency $f_I$, front-end preprocessing may also comprise further stages, such as the generation of baseband in-phase and quadrature components [7,8] representing a complex baseband signal. Therefore, here the general case of a complex-valued signal $r(m\Delta t)$ is assumed. For the recording time interval $\left[0,\left.M\mathsf{\Delta }t\right)\right.$, $M\in \mathbb{N}$, the finite sequence

$$\mathit{r}={\left(r_m\right)}_{m=0,..,M-1}\hspace{1em}\mathrm{with}\hspace{1em}{r}_m=r\left(\mathrm{m}\mathsf{\Delta }\mathrm{t}\right)$$

(1)

is obtained, which is hereafter referred to as an RF snapshot.

2.1.2. Software-Defined Receiver Acquisition Stage

In the present work, RF snapshots based on recordings in the E1/L1 frequency band undergo further digital signal processing, emulating the acquisition stage of a GNSS receiver. First, a concise overview thereof geared to [9,10] is given here.

In general, the acquisition stage aims at extracting coarse estimates of certain GNSS signal variables from the raw RF snapshot for PVT. Relevant signal variables encompass the code delay $\tau$ and the Doppler shift $f_D$ of a GNSS signal transmitted from a visible GNSS satellite. Estimates for $\tau$ and $f_D$ are commonly obtained by evaluating the CAF given in Equation (2) for coherent integration time $T_{CO}=N \Delta \mathrm{t}$, $N\in \mathbb{N}$.

$$Y^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)=\frac{1}{N}{\sum }_{n=0}^{N-1}{c}^{i,s}(n∆t-\widehat{\tau })r(n∆t)\mathrm{e}\mathrm{x}\mathrm{p}\left[-2\pi j\left({\widehat{f}}_D+f_I\right)n∆t\right]$$

(2)

The arguments ${\widehat{f}}_D$, $\widehat{\tau }$ of the CAF are candidate values for an estimation of the actual $\tau$ and $f_D$, respectively. $c^{i,s}\left(n\mathsf{\Delta }t\right)$ denotes the digital replica of the periodic spreading code signal $c^{i,s}$ which, besides the primary pseudo-random noise (PRN)-spreading code signal, may also contain a secondary code as well as a sub-carrier signal. The indices $i$ and $s$ indicate affiliation to a specific satellite of a constellation (as does the PRN number) and signal (e.g., Galileo E1-B), respectively. Similar to the notation in Equation (1), the subsequent sequences are introduced in order to cast the CAF in a more convenient form.

$${\mathit{c}}^{i,s}={\left(c_n^{i,s}\right)}_{n=0,‥,N-1}\hspace{1em}\mathrm{with}\hspace{1em}{c}_z^{i,s}=c^{i,s}\left(z\mathsf{\Delta }t\right) , z\in \mathbb{Z}$$

(3)

$$\mathit{x}\left({\widehat{f}}_D\right)={\left(x_n({\widehat{f}}_D)\right)}_{n=0,‥,N-1}\hspace{1em}\mathrm{with}\hspace{1em}{x}_n({\widehat{f}}_D)=r(n\mathsf{\Delta }t) \mathrm{e}\mathrm{x}\mathrm{p}\left[-2\pi j\left( {\widehat{f}}_D+f_I\right)n\mathsf{\Delta }t\right]$$

(4)

The CAF is evaluated on a rectangular grid $\mathcal{X}$, the code-Doppler search space; i.e., for

$$({\widehat{f}}_D,\widehat{\tau }) \in \mathcal{X}:=\left\{ k\mathsf{\Delta }f \left| k\in \mathbb{Z},\left|k\right|\le K \right.\right\}\times \left\{l\mathsf{\Delta }t| l \in {\mathbb{N}}_0 , l \le N-1\right\} .$$

(5)

$\mathsf{\Delta }f$ is an appropriate increment in the Doppler direction obeying $\mathsf{\Delta }f \le 2/\left(3T_{CO}\right)$ in order to allow for a sufficient resolution of the CAF. $K\in \mathbb{N}$ should be large enough to cover the range of expected Doppler shift values (with a magnitude up to 5 kHz for a static receiver). The coherent integration time is set as a multiple of the period of the spreading code signal $c^{i,s}$. Then, the evaluation of the CAF on $\mathcal{X}$ can be recast as

$$Y^{i,s}\left( {\widehat{f}}_D=k\mathsf{\Delta }f,\widehat{\tau }=l\mathsf{\Delta }t\right)={\left(IDFT\left[DFT\left[\mathit{x}\left(k\mathsf{\Delta }f\right)\right]\circ {DFT\left[{\mathit{c}}^{i,s}\right]}^{\ast }\right]\right)}_l,$$

(6)

enabling fast numerical evaluation of slices of the CAF for a constant Doppler shift ${\widehat{f}}_D$. The asterisk $\ast$ indicates the complex conjugate, $\circ$ denotes the Hadamard product and $DFT$, $IDFT$ the Discrete Fourier Transform and its inverse, respectively.

In the following, the squared absolute value

$${ S}^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)={\left|Y^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)\right|}^2$$

(7)

of the CAF for $\left({\widehat{f}}_D,\widehat{\tau }\right) \in \mathcal{X}$ is of interest. If ${\widehat{f}}_D$ and $\widehat{\tau }$ match the actual values of code delay and Doppler shift of an observed GNSS signal with spreading code signal $c^{i,s}$ contributing to the RF snapshot $\mathit{r}$, then $S^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)$ exhibits a more or less pronounced peak due to the auto- and cross-correlation properties of $c^{i,s}$. Here, a necessary condition for declaring acquisition of signal $s$ of satellite $i$ is that the appendant peak value of the metric (8), characterizing the signal-to-noise ratio, exceeds the threshold ${SNR}_{ac}$. Further conditions are given in context of the spoofing detection algorithm in Section 2.2.

$${SNR}^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right) :={\displaystyle \frac{S^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)-\mu \left(S^{i,s}\right) }{\sigma \left(S^{i,s}\right)}}$$

(8)

$\mathsf{\mu }\left(S^{i,s}\right)$ and $\mathsf{\sigma }\left(S^{i,s}\right)$ denote average and standard deviation, respectively, of the values $S^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)$ observed within the search space $\mathcal{X}$. If acquisition is declared, Doppler shift and code delay

$$\left({\widehat{f}}_D^{i,s},{\widehat{\tau }}^{i,s}\right)=\underset{\left({\widehat{f}}_D,\widehat{\tau }\right)\in \mathcal{X}}{\mathrm{arg\; max}}{S}^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)$$

(9)

pertaining to the most prominent peak are considered as first estimates for the respective actual values of the detected GNSS signal. Uniqueness is tacitly assumed here.

The signal-to-noise ratio can be increased by using

$$S_{NC,\mathit{\Lambda }}^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right) =\sum _{\lambda =1}^{\Lambda }{S}_{\lambda }^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)$$

(10)

instead of $S^{i,s}$, whereof the quantities $S_{\lambda }^{i,s}$ are individual realizations. Each $S_{\lambda }^{i,s}$ is calculated with an RF snapshot of length $T_{CO}$; $\Lambda$ is the number of consecutive snapshots used. The averaging effect of the non-coherent integration (10) attenuates the noise floor.

Under undisturbed conditions, an acquisition peak in $S^{i,s}$ is only caused by an authentic signal $s$ directly received from a visible satellite $i$. However, additional peaks in $S^{i,s}$ can be induced by interference that resembles the structure of the spreading code signal $c^{i,s}$, as is the case for multipath and, in particular, for spoofing. Here, the aim is to detect spoofing attacks by looking for additional, non-authentic peaks occurring in $S^{i,s}$ and for disturbances in a single peak caused by a spoofing signal. The received power of a spoofed signal is assumed to be comparable to that of the authentic signal so that the latter is not pushed into the noise floor of $S^{i,s}$, which would be the case for a substantial power advantage of the spoofing signal. Focus is laid on timely detection of the pull-off in a coherent spoofing attack where $\left({\widehat{f}}_D,\widehat{\tau }\right)$ of the authentic and the spoofing signal are very similar in the initial phase of the attack, so that the respective peaks in $S^{i,s}$ are then closely aligned and hardly distinguishable. A spoofing detection algorithm tailored to these needs is introduced in the next section.

2.2. Spoofing Detection Algorithm

The case that the coherent integration time $T_{CO}$ equals the primary code length is considered and the notation $S^{i,s}$ is used interchangeably with ${\mathrm{S}}_{NC,\Lambda }^{i,s}$, also for $\Lambda >1$.

The spoofing detection algorithm is only executed if the necessary condition ${SNR}^{i,s}({\widehat{f}}_D^{i,s},{\widehat{\tau }}^{i,s})>{SNR}_{ac}$ is fulfilled. The basic idea behind the algorithm is as follows. The observed data $S^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)$, $\left({\widehat{f}}_D,\widehat{\tau }\right)\in \mathcal{X},$ are preprocessed in a way that allows a suitable clustering algorithm, which is applied to the data resulting from the preprocessing (i.e., a list containing rescaled elements of $\mathcal{X}$) to recognize the presence of non-authentic, power-matched signals as the formation of clusters with particular properties, corresponding to signal peaks in $S^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)$.

By resorting to observed values of metric (8) in $\mathcal{X}$, the aforementioned preprocessing is achieved by filtering (11) with consecutive weighting and rescaling according to Equations (12) and (13).

$${\mathcal{Z}}^{i,s}≔\left\{\left({\widehat{f}}_D,\widehat{\tau }\right)\in \mathcal{X} | {SNR}^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)\ge {SNR}^{i,s}({\widehat{f}}_D^{i,s},{\widehat{\tau }}^{i,s})/2 \right\}$$

(11)

$$M^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)≔ \max \left\{1,⌊{SNR}^{i,s}({\widehat{f}}_D,\widehat{\tau })- {SNR}^{is}({\widehat{f}}_D^{i,s},{\widehat{\tau }}^{i,s})/2⌋\right\}$$

(12)

$${\mathcal{W}}^{i,s}≔ {\oplus }_{\left({\widehat{f}}_D,\widehat{\tau }\right)\in {\mathcal{Z}}^{i,s} }{\left(({\widehat{f}}_D/\delta f,\widehat{\tau }/\delta \tau )\right)}_{k=1,‥,M^{i,s}\left({\widehat{f}}_{D,}\widehat{\tau }\right)}$$

(13)

Here, $\oplus$ denotes the concatenation of sequences. The concatenation order is not relevant in our case. The brackets $⌊\dots ⌋$ represent the floor function. $\delta f>0$ and $\delta \tau >0$ are scaling parameters in the Doppler and code direction, respectively.

A mean shift clustering algorithm [11] with bandwidth $\beta >0$ is applied to the dimensionless scattered data ${\mathcal{W}}^{i,s}$ that contain duplicates with multiplicity $M^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)\in \mathbb{N}$ for weighting purposes, as explained in the next paragraph. A resulting cluster is considered ordinary if the standard deviation of the set of its constituents in the rescaled code and Doppler directions does not exceed the prescribed values ${\sigma }_{\tau }>0$ and ${\sigma }_f>0$, respectively. This definition is used in order to restrict the spoofing detection algorithm to clusters that emerge due to signal-like peaks in $S^{i,s}\left({\widehat{f}}_D,\widehat{\tau }\right)$ at the location of these peaks in $\mathcal{X}$ and to exclude clusters with vast extension that might emerge due to a high noise floor under difficult signal reception conditions. Likewise, a too large overall number of resulting clusters is supposed to be caused by higher isolated noise spikes under difficult signal reception conditions. In this case, acquisition is considered to have failed and no further analyses are carried out. Otherwise, if the overall number of resulting clusters does not exceed a reasonable prescribed maximal number $N_{cl}^{max}$, then acquisition is declared if there is at least one ordinary cluster, which here is considered as the detection of at least one pronounced signal peak. Then, a spoofing detection decision is carried out. A spoofing warning is triggered if the formation of more than one ordinary cluster occurs.

In the initial phase of a coherent, power-matched spoofing attack, a single authentic peak in $S^{i,s}$ is disturbed, which typically leads to the formation of at least two local maxima within this peak. The weighting based on multiplicity (12) is intended to induce local maxima in the density of points in ${\mathcal{W}}^{i,s}$ that should resemble the formation of the local maxima of $S^{i,s}$ in the disturbed peak. The applied mean shift clustering, in turn, is expected to form clusters according to local maxima in the local density of points in ${\mathcal{W}}^{i,s}$, cf. [11,12]. Due to this mechanism, the aforementioned preprocessing in combination with the particular properties of the applied mean shift clustering should allow for early detection of a pull-off in a coherent power-matched spoofing attack.

3. Data Sets

One of the two data sets used for evaluation of the spoofing detection algorithm is scenario 4 of the Texas Spoofing Test Battery (TEXBAT), hereafter denoted TEXBAT 4. It consists of baseband I-Q samples representing a snapshot-like complex-valued digital recording. It resulted from a raw RF recording in the L1 frequency band of approximately 7 min duration made with a static GNSS receiver where spoofing signals for GPS L1 C/A were incorporated not before 100 s of the sample elapsed. A counterfeited position shift of 600 m was induced by the power-matched spoofing signals [4]. According to [13], the position pull-off starts as soon as about 225 s of the sample have elapsed.

The second data set consists of modified versions of a real-valued RF snapshot of 4 ms length recorded in the E1 frequency band with 2-bit quantization at the Geodetic Observatory Wettzell with an IFEN SX3 Navigation Software Receiver. The modification consists of adding a computer-simulated spoofing signal for Galileo E1-B to the original digital RF snapshot on the software level. By applying distinct simulated spoofing signals for the aforementioned addition, multiple versions of an RF snapshot with incorporated spoofing situations are generated. For each acquired PRN, an individual position pull-off is mimicked by adding a spoofing signal with stepwise increased code delay (step size 0.05 µs) for that PRN, starting at the location of the authentic peak obtained from the original, unmodified snapshot. Thereby, for each code delay step a modified snapshot with a spoofing signal is created for a given PRN while the other PRNs are not manipulated. The collection of these modified snapshots is denoted GAL modified recording below.

Further details on parameters related to the latter digital samples and their evaluation with the methodology presented in Section 2 are given in

Table 1. Parameters related to digital samples and the calculation of the CAF.

Processed Sample	Frequency Band	${\mathbf{f}}_{\mathbf{I}} \left[\mathbf{H}\mathbf{z}\right]$	${\mathbf{f}}_{\mathbf{S}} \left[\mathbf{M}\mathbf{H}\mathbf{z}\right]$	$\mathbf{\Delta }\mathbf{f} \left[\mathbf{H}\mathbf{z}\right]$	${\mathbf{T}}_{\mathbf{C}\mathbf{O}}$ [ms]	$\mathsf{\Lambda }$
TEXBAT 4	L1	0.369 *	25	125	1	4
GAL modified recording	E1	5.00432 · 106	20	40	4	1

* This value is used according to the carrier offset reported in [13].

and

Table 2. Parameters for evaluation of the CAF with clustering techniques for spoofing detection.

Processed Sample	${\mathit{S}\mathit{N}\mathit{R}}_{\mathit{a}\mathit{c}}$	$\mathit{\delta }\mathit{f}$	$\mathit{\delta }\mathit{\tau }$	${\mathit{\sigma }}_{\mathit{f}}$	${\mathit{\sigma }}_{\mathit{\tau }}$	${\mathit{N}}_{\mathit{c}\mathit{l}}^{\mathit{m}\mathit{a}\mathit{x}}$	$\mathit{\beta }$
TEXBAT 4	30	$\mathsf{\Delta }f$	$1/f_s$	8	8	9	5
GAL modified recording	20	120 Hz	40 ns	8	8	9	2.5

.

4. Evaluation and Discussion

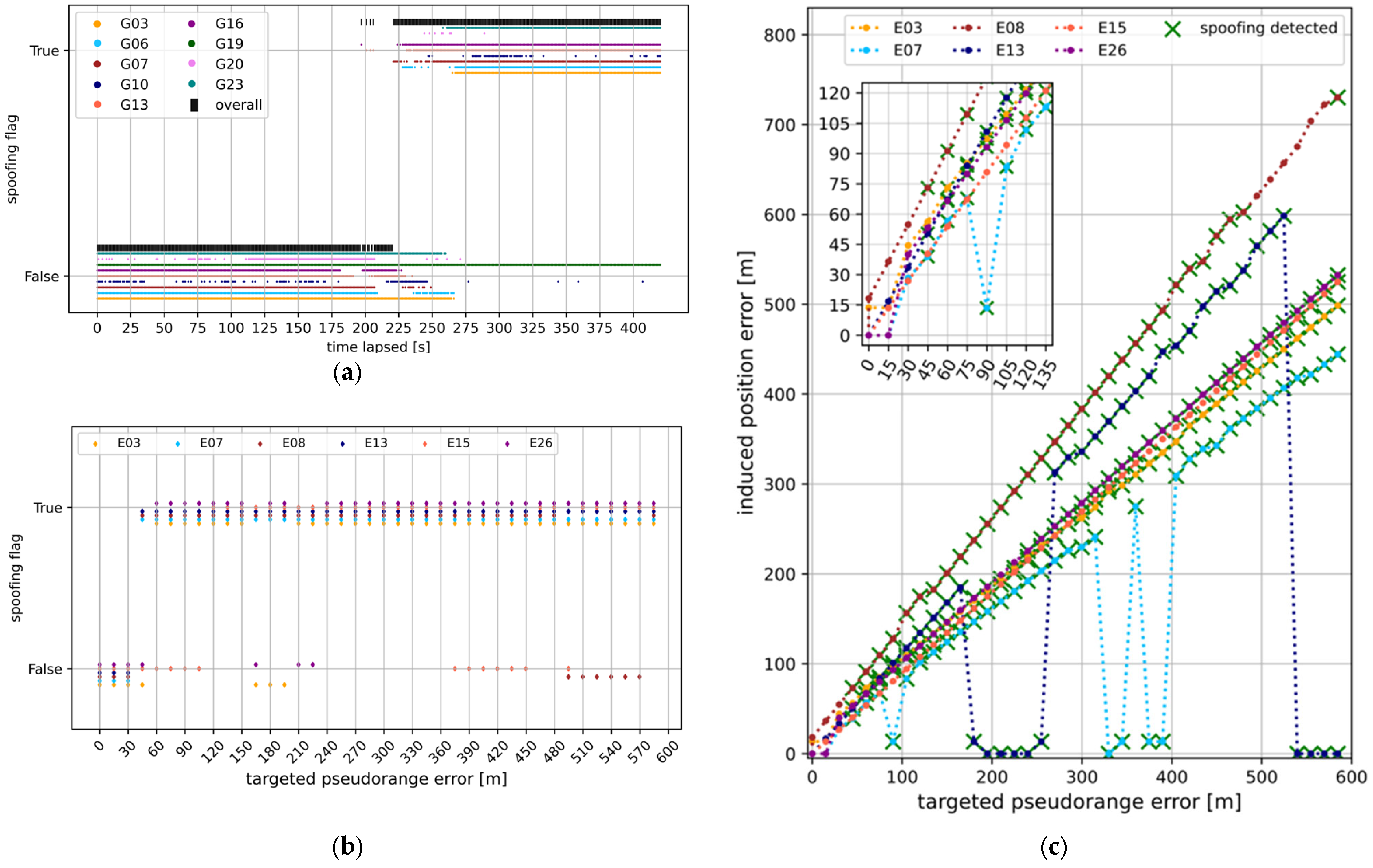
A first impression of the behavior of the proposed spoofing detection algorithm under normal conditions without spoofing as well as in the early phase of a pull-off is given in Figure 1 for TEXBAT 4: No false alarm is triggered if there is only the authentic peak present in $S^{16,L1 C/A}$. Moreover, the pull-off is already detected at an early stage where the authentic and spoofed peak are still clumped together. Here, the following desired property is exemplified. In the initial phase of the pull-off, more than one cluster results even when the scattered data ${\mathcal{Z}}^{i,s}$ appear like a single entity in the code–Doppler search space $\mathcal{X}$. Weighting (12) in combination with the use of the mean shift clustering algorithm is intended to work towards this behaviour. When the authentic and spoofed peak are clearly separated, there are exactly two clusters formed by the algorithm.

For a more comprehensive evaluation of the proposed spoofing detection algorithm with TEXBAT 4, a snapshot was taken from the data set once per second. The results of the application of the spoofing detection algorithm to these snapshots are summarized in Figure 2a. During the first 100 s no spoofing is present [13], which is correctly captured by the proposed algorithm since all evaluated spoofing flags are False then. According to [13], the actual pull-off in TEXBAT 4 starts at about 225 s. Here, this pull-off is detected in a timely manner, as the overall spoofing flag switches permanently to True just some seconds before. The first signs of the presence of spoofing signals are already detected before the nominal start of the pull-off. The first cases with spoofing flag True occurred for G16, G13 and G07 between 197 and 225 s elapsed. A visual inspection (not shown here) of $S^{16,L1 C/A}$, $S^{13,L1 C/A}$ and $S^{07,L1 C/A}$ confirmed the correctness of the respective values of the spoofing flags: When the spoofing flag is True, the present peaks exhibit pronounced deformations, with noticeable local maxima. For G10 there are four isolated occurrences with spoofing flag False after the beginning of the pull-off. Inspecting $S^{10,L1 C/A}$ suggests that these are misclassifications since there are broad deformations of the peak in $S^{10,L1 C/A}$ (partly with an additional pronounced local maximum) below the threshold associated with the SNR filtering (11), which consequently do not trigger a spoofing alert. Furthermore, there are rather small but clearly perceptible deformations in $S^{19,L1 C/A}$ after beginning of the pull-off, which are not strong enough to trigger a spoofing alert, so the spoofing flag remains False all the time for G19. Overall, if deformations in $S^{i,L1 C/A}$ are only marginal, or if there is an intermittent phase where the matched-power condition is not fulfilled, the spoofing flag can switch between True and False several times.

For the GAL modified recording, the resulting spoofing flags for individual PRNs in the course of the mimicked pull-offs are depicted in Figure 2b. For E15 the spoofing signal initially overpowers the authentic one so that the latter is pushed below the SNR threshold of filter (11) in the initial phase. For this reason, spoofing is not detected for E15 for targeted pseudorange errors smaller than approximately 120 m. For all other PRNs, the pull-off is detected as soon as the targeted pseudorange error reaches 45 m or 60 m. Altogether, occurrences of a False spoofing flag for larger targeted pseudorange errors is due to a power advantage of the spoofing signal, which pushes the authentic signal peak in $S^{i,E1-B}$ below the threshold related to the SNR filtering (11). For the GAL modified recording, the effect of the mimicked pull-offs on the estimated position is shown in Figure 2c. For each PRN-specific pull-off, the induced error (i.e., distance between authentic and spoofed position) in the single point positioning (SPP) solution is depicted. SPP is performed based on the peak code delay values in $S^{i,E1-B}$ from acquisition by resorting to navigation data from archived RINEX files [14]. The simulated spoofing signals successively induce a position error up to about 750 m. Exceptions are found for E07 and E13 where the authentic peaks in $S^{07,E1-B}$ and $S^{13,E1-B}$ overpower the spoofed ones several times, causing the induced position error to drop. Then, a position error that slightly differs from 0 m can emerge due to the presence of the spoofing signal still acting as interference that may degrade the position estimation.

For the GAL modified recording, the behavior of the spoofing detection algorithm under unspoofed conditions as well as for the mimicked spoofing pull-off is exemplified in Figure 3. The desired properties concerning false alarms and early detection are observed, as similarly found in Figure 1 for TEXBAT 4. In addition, the ability of the algorithm to cope with a data bit sign transition within the coherent integration period is demonstrated for the GAL modified recording in Figure 3d: Despite of the split of the authentic main correlation peak into two sub-peaks in the Doppler direction, which can occur due to a bit sign transition [15], these sub-peaks are recognized as belonging together by the clustering algorithm. No additional cluster is formed here. This behavior was also observed for this main peak split in absence of the spoofing signal, which demonstrates that the algorithm is not prone to false alarms in the case of a bit sign transition with a respective split of the authentic main peak. This behavior is obtained by setting an appropriate value for the scaling parameter $\delta$f in the Doppler direction of the search space $\mathcal{X}$.

5. Concluding Remarks

A spoofing detection algorithm was proposed that shall enable early detection of the pull-off in a coherent power-matched spoofing attack by monitoring the absolute value of the CAF with particular clustering techniques. The evaluation of the algorithm for GPS L1 C/A with the TEXBAT 4 data set as well as for Galileo E1-B with the introduced GAL modified recording demonstrated the usability of the spoofing detection algorithm within the aforementioned intended scope. As long as the condition concerning power-matching is fulfilled, not only the desired early detection is achieved, but also spoofing detection after separation of the authentic and spoofed signal peak in the CAF, covering the whole code–Doppler search space. In the evaluation, the proposed method appeared to be robust against false alarms. However, false alarms due to multipath can be expected. The proposed algorithm exhibited a lack of sensitivity in a few marginal cases with only a modest deformation of the CAF correlation peak. An adjustment of tunable parameters in Table 1 and Table 2 could help to increase sensitivity for such marginal cases. Moreover, some missed detections due to a violation of the matched-power condition could be circumvented by performing additional, similar detection analyses for further threshold levels for $SN{R}^{i,s}$ besides that in Eq. (11). In this context it should be noted that false negative results of the proposed CAF monitoring algorithm due to a power advantage of the spoofing signal could effectively be countered by simultaneously applying in-band power monitoring, as similarly pointed out in [4]. Altogether, the proposed algorithm appears to be a useful complementary means for spoofing detection that can be used in combination with other detection techniques in order to increase resilience against spoofing attacks.