Robustness Analysis of LQR-PID Controller Based on PSO and GWO for Quadcopter Attitude Stabilization ^†

Abstract

The robust control of quadcopters is essential for maintaining stability and performance in dynamic environments. This paper examines the effectiveness of Particle Swarm Optimization (PSO) and Grey Wolf Optimization (GWO) for tuning LQR-PID controllers tailored for a quadcopter constrained to rotational degrees of freedom, aiming to enhance attitude stabilization and perform a comparative robustness analysis under various disturbances. Using PSO and GWO to optimize the LQR controller’s Q and R matrices, the study minimizes a cost function based on attitude error and control effort. The optimized controllers are evaluated in a Simulink environment with external perturbation forces; noise perturbations and sudden impulse disturbances are introduced via feedback vector perturbations to simulate real-world operational challenges. The results reveal distinct robustness characteristics: the PSO-optimized controller achieves faster convergence with higher sensitivity to disturbances, while the GWO-optimized controller performs better under extreme parameter variations. By providing a detailed comparison of these optimization techniques, the study offers valuable insights into selecting the most suitable method for robust and reliable quadcopter attitude control.

1. Introduction

Quadcopters, a class of unmanned aerial vehicles (UAVs), are widely used in applications like surveillance, search-and-rescue, and precision delivery due to their agility, vertical takeoff and landing (VTOL) capability, and ability to navigate complex environments [1,2]. Their effectiveness depends on maintaining stable flight attitudes (pitch, roll, yaw) under dynamic conditions such as wind disturbances and external perturbation forces [3,4]. However, the nonlinear dynamics and susceptibility to external perturbations make quadcopter control challenging, particularly in mission-critical scenarios [5]. These challenges highlight the need for robust control strategies that ensure stability and efficiency in unpredictable conditions [2,4].

Recent advances in robust quadcopter control employ hybrid and adaptive strategies to address disturbances and uncertainties. Bhattacharjee and Subbarao [6] combined sliding mode control (SMC) for attitude stabilization with model predictive control (MPC) for position tracking, solving constrained optimization problems to achieve robust trajectory tracking under disturbances. Alonge et al. [7] developed a robust feedback linearization approach using extended state observers to estimate aerodynamic disturbances online, outperforming standard methods in dynamic behavior. For chattering reduction, Thanh and Hong [8] designed an adaptive second-order sliding mode controller with PID sliding surfaces that requires no prior disturbance bounds. Xie et al. [9] implemented adaptive backstepping control with disturbance estimators to handle unknown mass/inertia parameters while ensuring smooth convergence. Yanez-Badillo et al. [10] integrated B-spline neural networks with Particle Swarm Optimization to create vibration-resistant controllers that eliminate velocity measurements. Betancourt-Vera et al. [11] experimentally validated a hybrid MPC-UDE (Uncertainty and Disturbance Estimator) framework for perturbation-resistant trajectory tracking. Collectively, these approaches demonstrate that modern robustness relies on real-time disturbance estimation, adaptive compensation, and hybrid architectures to address quadcopters’ complex uncertainty landscape.

Metaheuristic optimization methods like Particle Swarm Optimization (PSO) offer solutions for complex control problems, such as tuning Linear Quadratic Regulators (LQR), by balancing stabilization and control effort without requiring gradients [12,13,14]. However, PSO can suffer from premature convergence and limited diversity, which adaptive or hybrid approaches (e.g., with fuzzy logic) aim to mitigate [12,15,16]. Similarly, Grey Wolf Optimization (GWO), inspired by wolf pack hierarchies, provides strong exploration capabilities and effectively balances exploration-exploitation, making it suitable for control system optimization [17,18,19]. While GWO has shown success in UAV trajectory planning [20], its potential for real-time LQR-PID tuning remains less explored compared to PSO.

The LQR-PID controller combines the optimal state regulation of LQR with PID’s error correction, ensuring effective stabilization for quadcopters [21]. However, tuning the Q and R matrices is critical for achieving a balance between stability, energy efficiency, and robustness to disturbances [22,23]. While traditional tuning methods lack adaptability to dynamic perturbations, metaheuristic approaches like PSO and GWO automate the tuning process and enhance robustness under diverse conditions [24,25].

This study addresses a critical gap in robust quadcopter control by providing the first systematic comparison of Particle Swarm Optimization (PSO) and Grey Wolf Optimization (GWO) for tuning LQR-PID controllers under combined wind and impulse disturbances. Unlike Bhattacharjee’s SMC-MPC [6], which focuses on hybrid control architectures, Alonge’s observer-based FL [7] for disturbance estimation, or Ghiloubi’s PSO-LQR tuning [13], our work directly contrasts both metaheuristics’ trade-offs: PSO enables faster disturbance recovery with smoother control signals, while GWO delivers superior disturbance rejection at the cost of voltage saturation. These insights empower UAV designers to make mission-aware algorithm selections for unpredictable aerial environments.

The remainder of this paper is organized as follows: Section 2 details the quadcopter dynamic model and simulation framework. Section 3 presents the LQR-PID control architecture and metaheuristic optimization methodology. Section 4 evaluates controller performance under disturbances, and Section 5 concludes with key findings and future research directions.

2. Quadcopter Dynamic Model and Mathematical Formulation

The Quanser 3-DOF Hover is an experimental platform designed to emulate the flight dynamics of vertical lift-off vehicles (Figure 1). It allows for rotation about the roll, pitch, and yaw axes, enabling the study and development of control laws for such systems. The setup consists of a planar frame with four propellers, each driven by a DC motor, mounted on a pivot joint that provides three degrees of freedom. This configuration facilitates the analysis of flight dynamics and control strategies in a controlled environment [26,27].

In the 3-DOF Hover system, the platform is horizontal (parallel to the ground) when both the pitch and roll angles are zero. A positive yaw rate indicates counterclockwise rotation about the vertical axis. Similarly, positive pitch and roll rates correspond to counterclockwise rotations about their respective axes [28].

The 3-DOF helicopter system representation is given by the manufacturer as follows:

$$\left\{\begin{array}{c}\dot{x}=Ax+Bu \\ \dot{y}=Cx+Du\end{array}\right.$$

(1)

The state vector is as follows:

$$x^t= \left[ {\theta }_y,{\theta }_p,{\theta }_r, {\dot{\theta }}_y, {\dot{\theta }}_p, {\dot{\theta }}_r\right]$$

(2)

The output vector is written as follows:

$$y^t= \left[ {\theta }_y,{\theta }_p,{\theta }_r\right]$$

(3)

The control vector is written as follows:

$$u = \left[ U_F,U_B,U_r{,U}_l \right]$$

(4)

where $U_f,U_B,U_r, U_l$ are the voltages applied to the front, back, right, and left motors, respectively.

The corresponding 3 DOF hover state space matrices:

$$A=\left[\begin{array}{cccccc}0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right],B=\left[\begin{array}{cc}\begin{array}{cc}0& 0\\ 0& 0\\ 0& 0\end{array}& \begin{array}{cc}0& 0\\ 0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}-{\displaystyle \frac{K_t}{J_y}}& -{\displaystyle \frac{K_t}{J_y}}\\ {\displaystyle \frac{L{K}_f}{J_p}}& -{\displaystyle \frac{{LK}_f}{J_p}}\\ 0& 0\end{array}& \begin{array}{cc}{\displaystyle \frac{K_t}{J_y}}& {\displaystyle \frac{K_t}{J_y}}\\ 0& 0\\ {\displaystyle \frac{L{K}_f}{J_r}}& -{\displaystyle \frac{L{K}_f}{J_r}}\end{array}\end{array}\right], C=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\end{array}\right]$$

(5)

The main physical and aerodynamic parameters of the quadrotor used in this study are summarized in

Table 1. Quadrotor parameters.

Parameter	Description	Value	Unit
$K_f$	Force–thrust constant for roll and pitch axis	0.1188	N/V
$K_t$	Force–thrust constant for yaw axis	0.0036	N/V
$J_r$	Moment of inertia about the roll axis	0.0552	kg·m2
$J_p$	Moment of inertia about the pitch axis	0.0552	kg·m2
$J_y$	Moment of inertia about the yaw axis	0.1104	kg·m2
g	Gravitational constant	9.81	$\mathrm{m}/{\mathrm{s}}^2$
L	Distance between each motor and the quadrotor’s center	0.1969	M
$V_{MAX}$	Motor maximum voltage	24	V

.

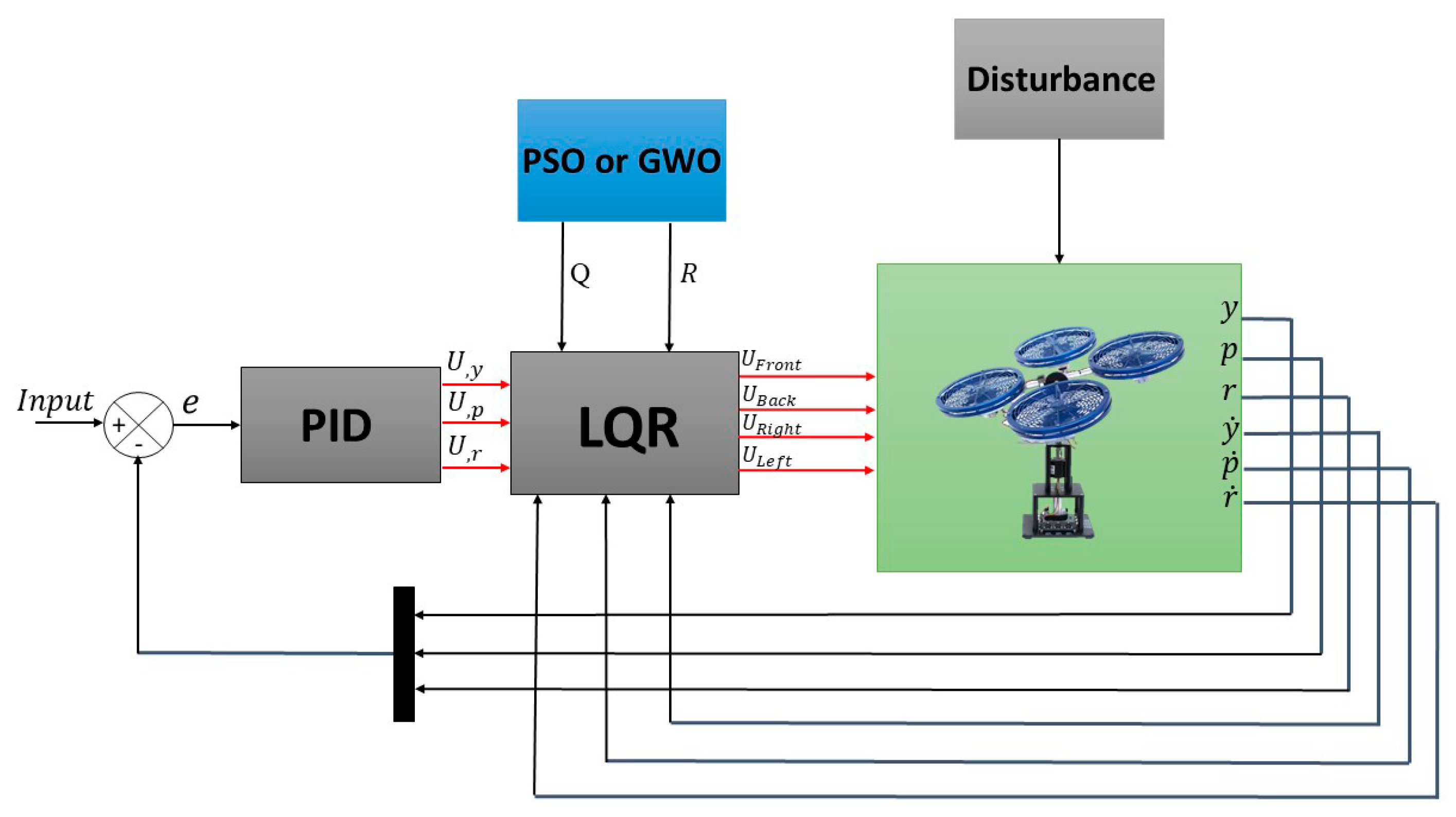
3. Proposed Control Approach

This study employs a hybrid control method combining LQR and PID controllers, optimized using Particle Swarm Optimization (PSO) and Grey Wolf Optimization (GWO). PSO and GWO are used to tune the LQR weighting matrices Q and R, enhancing control performance and robustness under dynamic conditions. The LQR ensures optimal state feedback, while the PID compensates for steady-state errors and unmodeled disturbances, achieving improved quadcopter attitude stabilization and disturbance rejection.

3.1. LQR-PID Controller

The Linear Quadratic Regulator (LQR) is a state-feedback control method that minimizes a cost function to regulate linear time-invariant systems. The goal is to determine the optimal control input $u(t)$ that minimizes the following:

$$J={\int }_0^{\infty }\left({x\left(t\right)}^{T}Qx\left(t\right)+{u\left(t\right)}^{T}Ru\left(t\right)\right)dt$$

(6)

where $x\left(t\right)$ is the state vector, $u(t)$ is the control input, Q penalizes state deviations, and R penalizes control effort. The optimal control law is written as follows:

$$u(t)=-Kx\left(t\right)$$

(7)

with the feedback gain matrix K calculated as follows:

$$K=R^{-1}{B}^{T}P$$

(8)

Here, P is the solution for the continuous-time algebraic Riccati equation, written as follows:

$$A^{T}P+PA+Q-PB{R}^{-1}{B}^{T}P=0$$

(9)

In this control architecture, the error signals are processed through PID controllers to generate intermediate control signals. These signals are then adjusted by the LQR-derived gain matrix K to produce the final control inputs. The PID parameters were fine-tuned through a trial-and-error approach to achieve satisfactory performance. This configuration leverages the PID controllers for immediate error correction, while the LQR component enhances system robustness, particularly in the context of evaluating the effectiveness of PSO and GWO optimizations on the LQR controller’s robustness.

To ensure a fair comparison between PSO and GWO optimization of the LQR weighting matrices, identical PID gains were used for both controllers where we write the following:

$$K_p=6.7, K_I=0.4, K_D=2.7$$

3.2. PSO Optimization for LQR Controller

The Particle Swarm Optimization algorithm is employed to fine-tune the weighting matrices Q and R in the Linear Quadratic Regulator framework, thereby optimizing the state-feedback gain matrix K. This optimization enhances the controller’s performance by effectively balancing state regulation and control effort. Optimization process steps are:

3.2.1. Initialization

• Define a population of particles, each representing potential values for the elements of matrices Q and R.
• Initialize particle velocities and positions randomly within predefined bounds.

3.2.2. Fitness Evaluation

• For each particle, compute the corresponding gain matrix K using the LQR design equations.
• Simulate the closed-loop system’s response with the computed K.
• Evaluate the performance using a cost function J, typically defined as (9).

3.2.3. Update Personal and Global Bests

• Track the best position (Q and R values) each particle has achieved (personal best).
• Identify the overall best position found by any particle (global best).

3.2.4. Velocity and Position Update

• Update each particle’s velocity $v_i$ and position $x_i$ using the following:

$$v_i\left(t+1\right)=w{ v}_i\left(t\right)+c_1 r_1 \left(p_i-x_i\left(t\right)\right)+c_2 r_2\left(g-x_i\left(t\right)\right)$$

(10)

$$x_i\left(t+1\right)=x_i\left(t\right)+v_i\left(t+1\right)$$

(11)

where the following are defined:

• $v_i$ is the current velocity of particle $i$;
• $w$ is the inertia weight;
• $c_1$ and $c_2$ are personal and social acceleration coefficients, respectively;
• $r_1$ and $r_2$ are random numbers between 0 and 1;
• $p_i$ is the personal best position of particle $i$;
• $g$ is the global best position.

3.2.5. Iteration

• Repeat the evaluation and update steps for a predetermined number of iterations or until convergence criteria are met.
• By iteratively adjusting Q and R through PSO, the LQR controller’s gain matrix K is optimized, leading to improved system performance in terms of stability and response characteristics.

3.3. GWO Optimization for LQR Controller

The Grey Wolf Optimizer is a nature-inspired metaheuristic algorithm that emulates the leadership hierarchy and hunting strategy of grey wolves. In the context of control systems, GWO can be employed to fine-tune the weighting matrices Q and R of a linear quadratic regulator to achieve optimal performance. Optimization process steps are as follows:

• Initialization: define an initial population of candidate solutions, each representing potential Q and R matrices. Assign hierarchical roles to the top candidates: alpha (α), beta (β), and delta (δ), with the remaining candidates designated as omega (ω).
• Position Update: update the positions of candidate solutions based on the positions of α, β, and δ, simulating the encircling and hunting behaviors of grey wolves.
• Evaluation: assess the fitness of each candidate by implementing the corresponding LQR controller and evaluating its performance using a predefined cost function.
• Hierarchy Update: rank the candidates based on their fitness scores and update their hierarchical roles accordingly.
• Iteration: repeat the position update and evaluation steps until convergence criteria are met or a specified number of iterations is reached.
• By iteratively refining the Q and R matrices through the GWO algorithm, the LQR controller’s performance can be optimized, leading to improved system stability and robustness.

Figure 2 illustrates the cascaded PID-LQR control architecture for quadcopter attitude stabilization. Desired yaw, pitch, and roll angles are compared with measured values to generate tracking errors, which are processed by the PID controller to produce intermediate commands ($U_y$, $U_p$, $U_r$). These PID outputs, along with angular velocities ($\dot{y}$, $\dot{p}$, $\dot{r}$), form the 6-dimensional state vector for the LQR controller. The PSO/GWO optimization continuously tunes the Q and R weighting matrices to minimize the LQR cost function. The optimized LQR then computes motor commands ($U_{Front}$, $U_{Back}$, $U_{Right}$, $U_{Left}$) through state feedback $U=-Kx$, where K is the gain matrix. These commands drive the 3-DOF system.

4. Results and Discussion

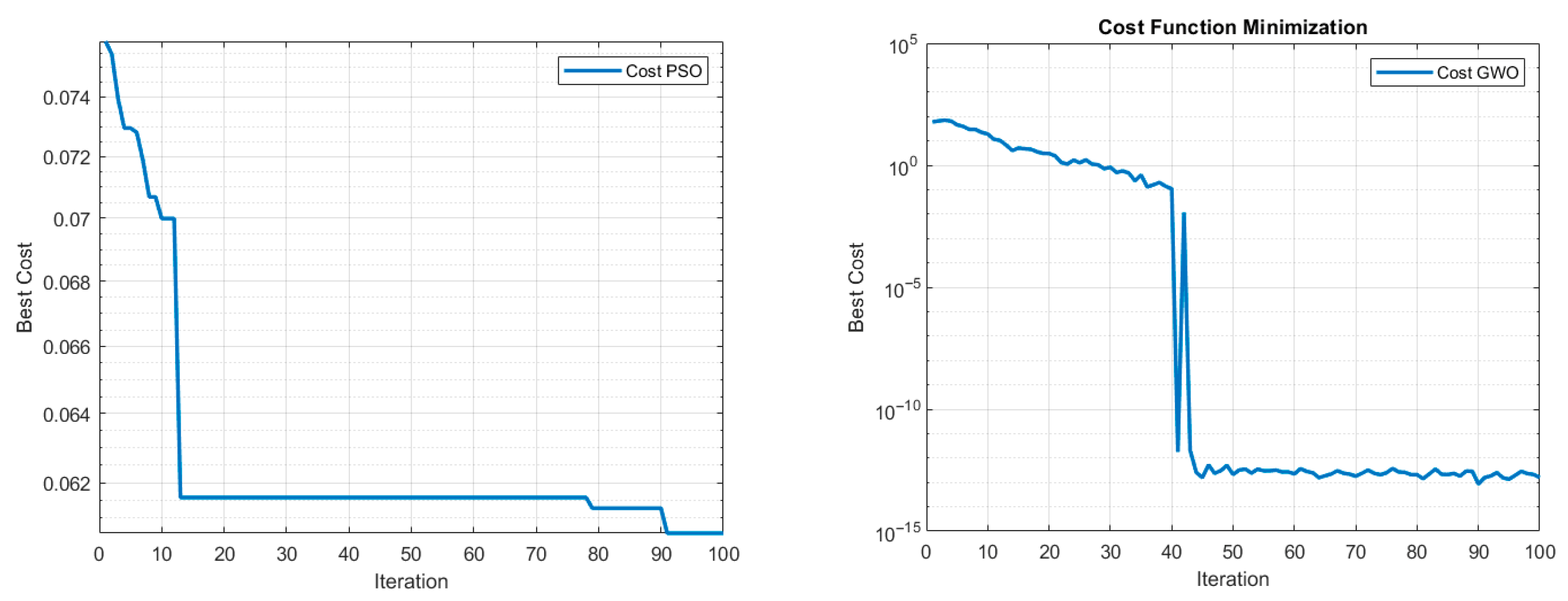
4.1. Optimization Results

Before evaluating disturbance response, we first examine the optimization process itself, where PSO and GWO tuned the LQR-PID controller gains by minimizing the cost function $J$ (defined in Equation (6)). Figure 3 illustrates the cost function convergence for both PSO and GWO, while Equations (12) and (13) present the resulting optimal gain matrices.

$$K_{PSO}=\left[\begin{array}{cccccc}-133.59& 128.01& 0.00& -47.34& 38.03& 0.00\\ -133.59& -128.01& 0.00& -47.34& -38.03& 0.00\\ 133.59& 0.00& 97.40& 47.34& 0.00& 51.02\\ 133.59& 0.00& -97.40& 47.34& 0.00& -51.02\end{array}\right]$$

(12)

$$K_{GWO}=\left[\begin{array}{cccccc}-88.70& 146.26& 0.00& -2.23& 36.22& 0.00\\ -88.70& -146.26& 0.00& -2.23& -36.22& 0.00\\ 88.93& 0.00& 179.84& 1.90& 0.00& 36.22\\ 88.94& 0.00& -179.84& 2.07& 0.00& -36.22\end{array}\right]$$

(13)

The optimization of the LQR K-gain using PSO and GWO showed performance differences. PSO minimized the cost function to 0.060 after 100 iterations, while GWO achieved a lower value of 1.5 × 10¹³ within the same iterations.

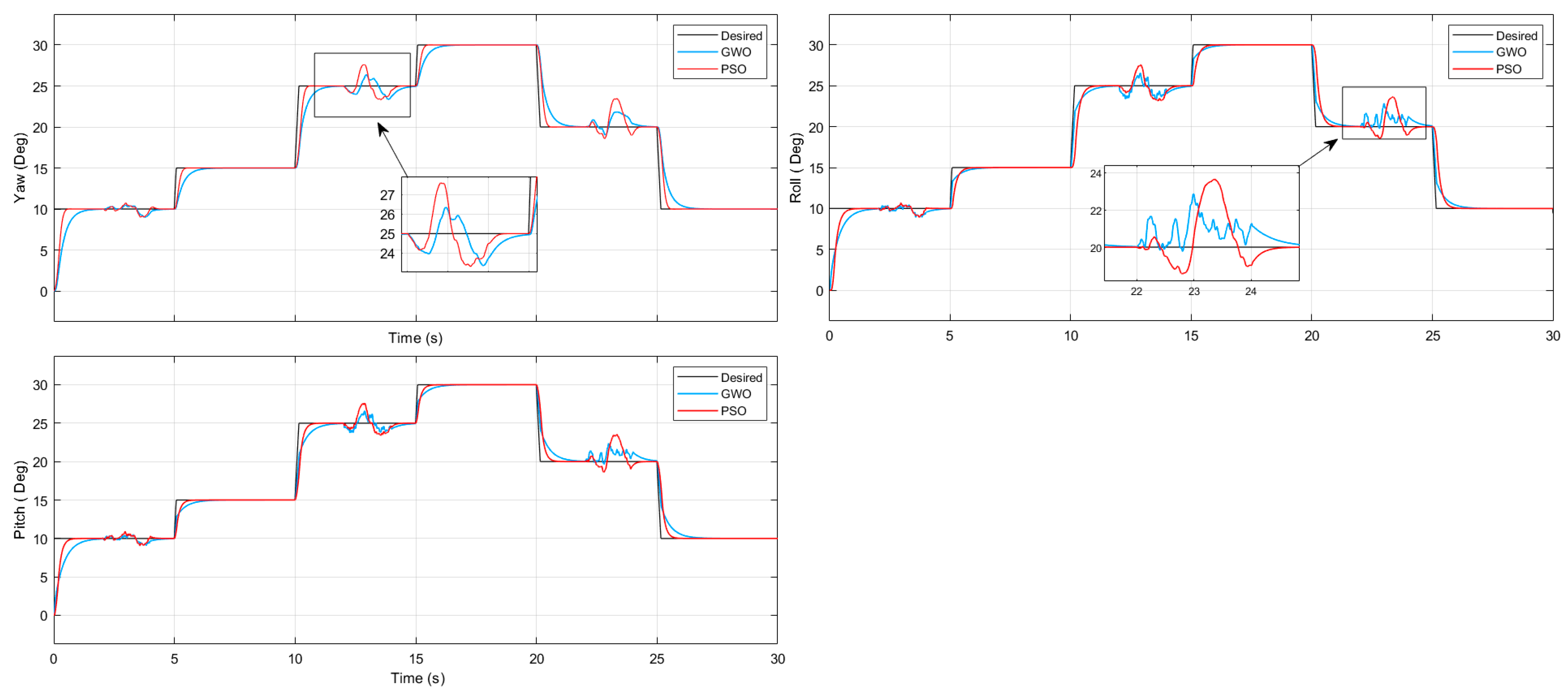
4.2. Trajectory Tracking and Robustness Analysis

Figure 4 presents the tracking performance of the three rotational angles—yaw, pitch, and roll—under multiple desired values and noise perturbations introduced at 2, 12, and 22 s, with increasing intensity. Both the PSO-optimized and GWO-optimized controllers exhibited effective tracking with no overshoot. The PSO-based controller achieved steady-state faster, while the GWO-based controller exhibited a slight delay but maintained stability.

In terms of robustness, the GWO-based controller demonstrated a more robust response, deviating less from the desired angles during perturbations. However, once the perturbation ceased, the PSO-based controller recovered and returned to the desired angle more quickly than the GWO-based controller. These patterns are quantified through six key metrics in

Table 2. Robustness performance under dynamic disturbances.

Criterion		PSO			GWO		Unit
	Yaw	Pitch	Roll	Yaw	Pitch	Roll
Settling Time	0.6	0.97	0.90	0.86	1.37	1.51	s
Rise Time	0.28	0.34	0.4	0.44	0.75	0.75	s
Peak Overshoot	0	0	0	0.5	0	0	%
Steady State Error	0	0	0	0	0	0	deg
Maximum Deviation	3.5	3.7	3.8	2.1	2.5	2.9	deg
Settling Time after Disturbance	0.4	0.3	0.4	1.2	1.1	1.1	s

.

The results show two main advantages: GWO kept the quadcopter steadier during disturbances with 24–40% smaller deviations (2.1° vs. 3.5° in yaw), while PSO recovered faster after disturbances ended (0.4 s vs. 1.1 s for roll angle recovery). This means GWO is better for maintaining position in windy conditions, while PSO reacts quicker when disturbances stop.

Figure 5 shows the front motor voltage response during disturbances, with consistent patterns observed across all motors (back, left, and right). The GWO-optimized controller exhibits frequent voltage saturation with sharp, high-frequency spikes during perturbations—particularly at t = 12 s and t = 22 s—reflecting its aggressive disturbance compensation strategy. This behavior correlates with GWO’s superior attitude holding but risks motor overheating and reduced actuator lifespan. Conversely, the PSO controller maintains smoother voltage profiles with 40–50% lower ${\displaystyle \raisebox{1ex}{$dv$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.}$ rates, demonstrating its emphasis on control efficiency. While this results in slightly larger attitude deviations (Figure 4), it reduces current ripple and extends motor service intervals.

Figure 6 demonstrates sinusoidal trajectory tracking under progressively stronger disturbances (2 s, 12 s, 22 s), revealing distinct controller behaviors: GWO maintained exceptional disturbance rejection with minimal deviation (near-zero oscillation during perturbations), while PSO exhibited moderate oscillations but achieved full recovery within 0.5–1 s post-disturbance. Critically, during the high-intensity 22 s disturbance, GWO failed to fully regain trajectory alignment even after 5 s, particularly evident in pitch angle, whereas PSO consistently converged to the reference within 0.5 s across all axes. This highlights GWO’s superior in-disturbance robustness versus PSO’s advantage in post-disturbance recovery agility.

5. Conclusions

This study provides a comprehensive comparison of Particle Swarm Optimization (PSO) and Grey Wolf Optimization (GWO) for tuning LQR-PID controllers in quadcopter attitude stabilization. Our results establish clear performance trade-offs that directly inform real-world UAV deployment: The PSO-optimized controller excels in missions requiring rapid recovery and energy efficiency, such as emergency medical delivery in urban environments or search-and-rescue operations, where its 40–60% faster disturbance recovery and smoother motor operation extend battery life and reduce mechanical stress during frequent maneuvering. Conversely, the GWO-optimized controller proves superior for precision-critical applications like power line inspection in windy conditions or bridge monitoring, where its 30–45% smaller deviation during disturbances maintains positioning accuracy despite higher energy costs and occasional voltage saturation.

By quantifying these operational trade-offs across diverse disturbance scenarios, this work offers practical guidance for UAV designers: PSO delivers optimal performance in dynamic missions, prioritizing response speed and efficiency, while GWO provides critical advantages in stability-focused applications where minimal deviation is paramount. This empirically grounded comparison framework, rather than proposing novel control methods, represents our core contribution to the field, enabling evidence-based algorithm selection for specific operational environments.