Numerical Simulation for Dual Solid Particle Separation Using Fluidized Bed †
Abstract
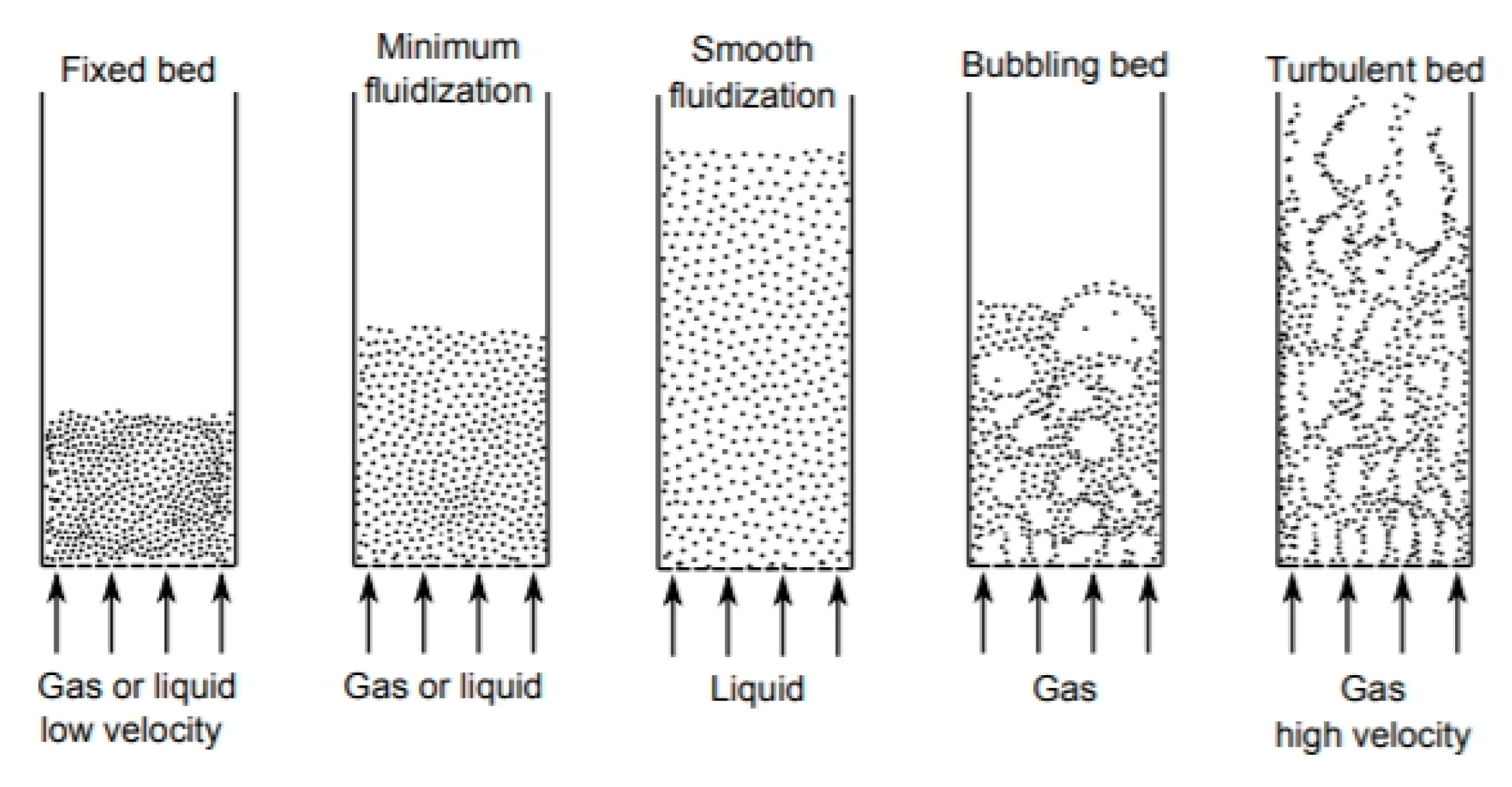
1. Introduction
2. Governing Equations
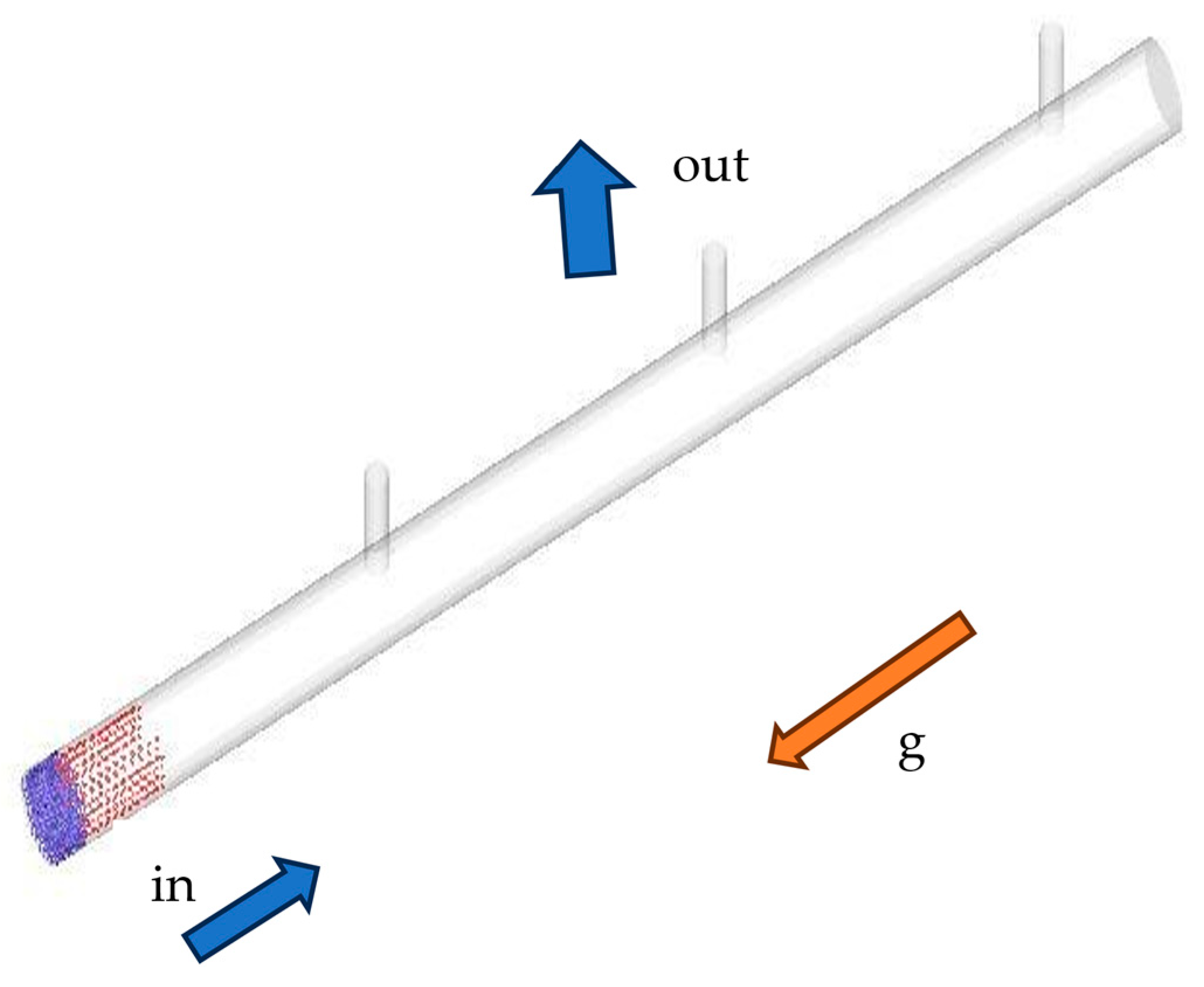
3. Simulation Set Up
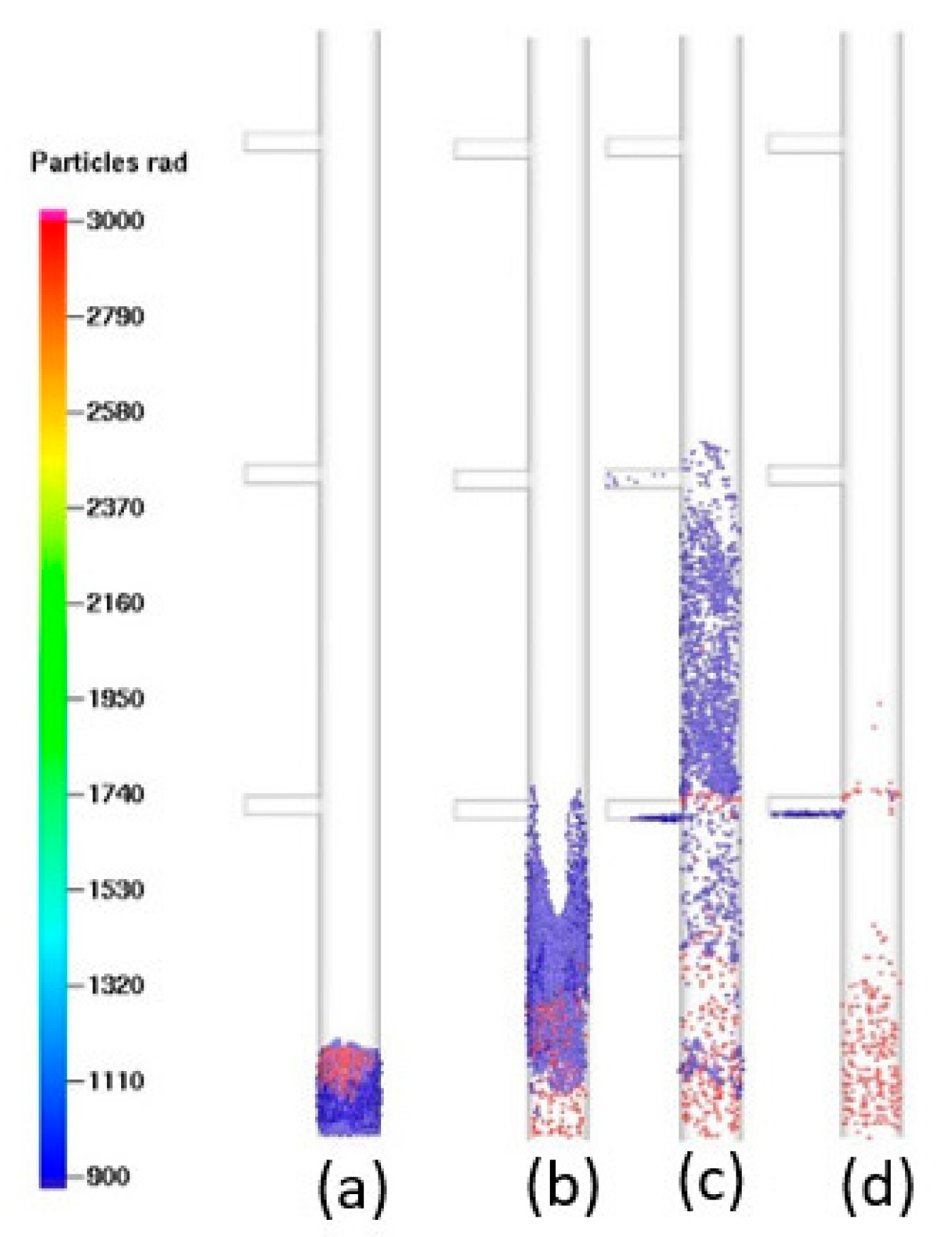
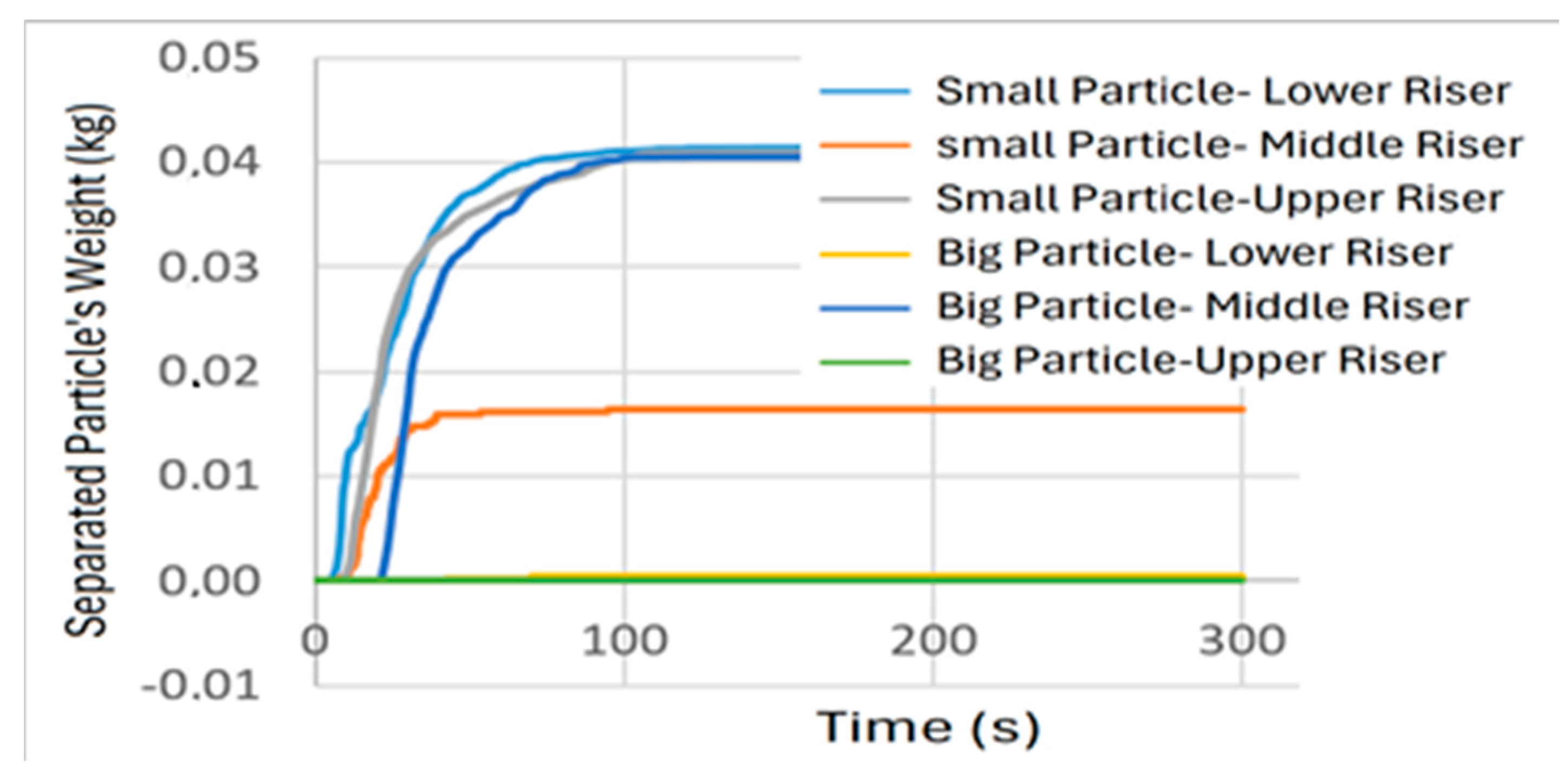
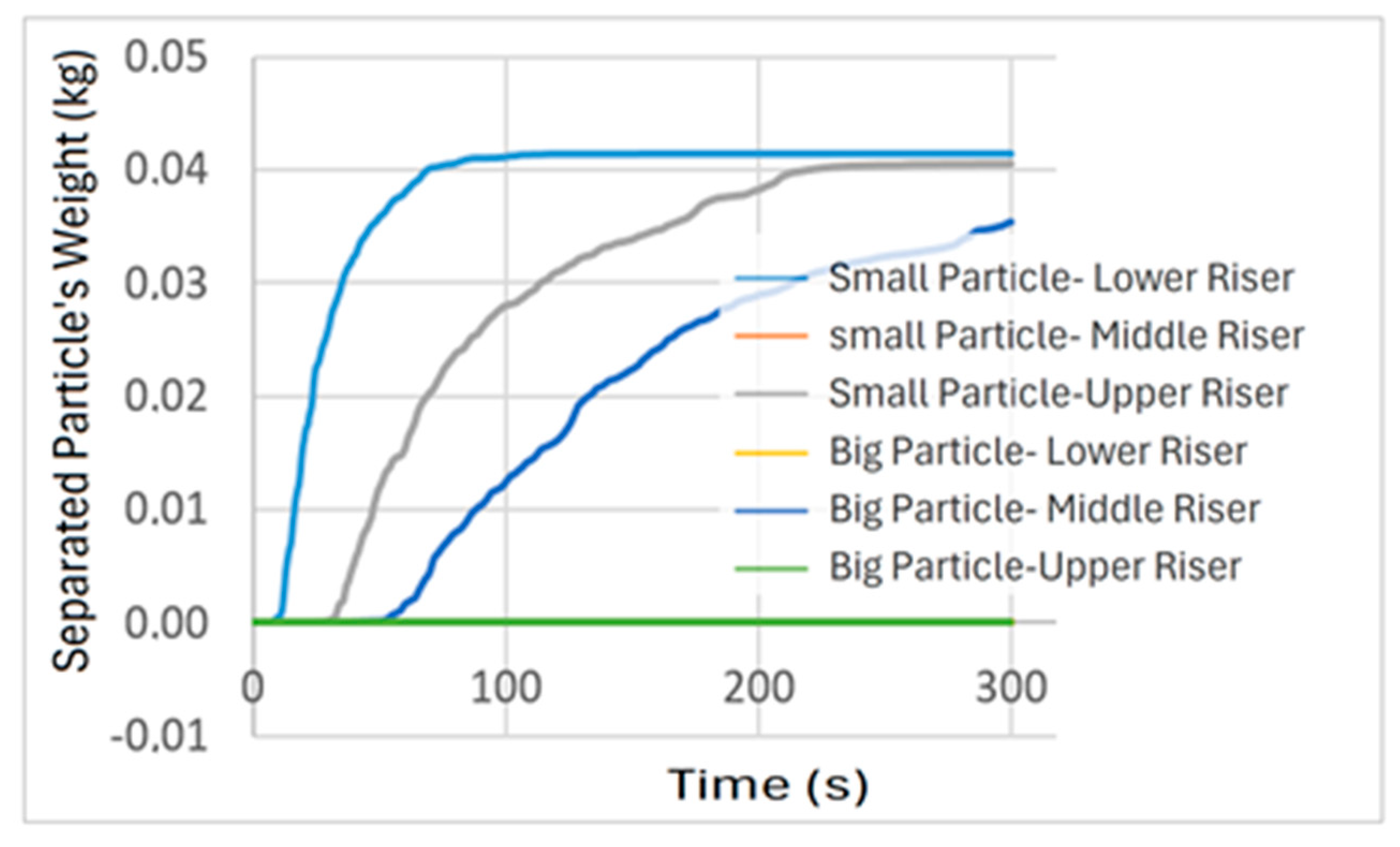
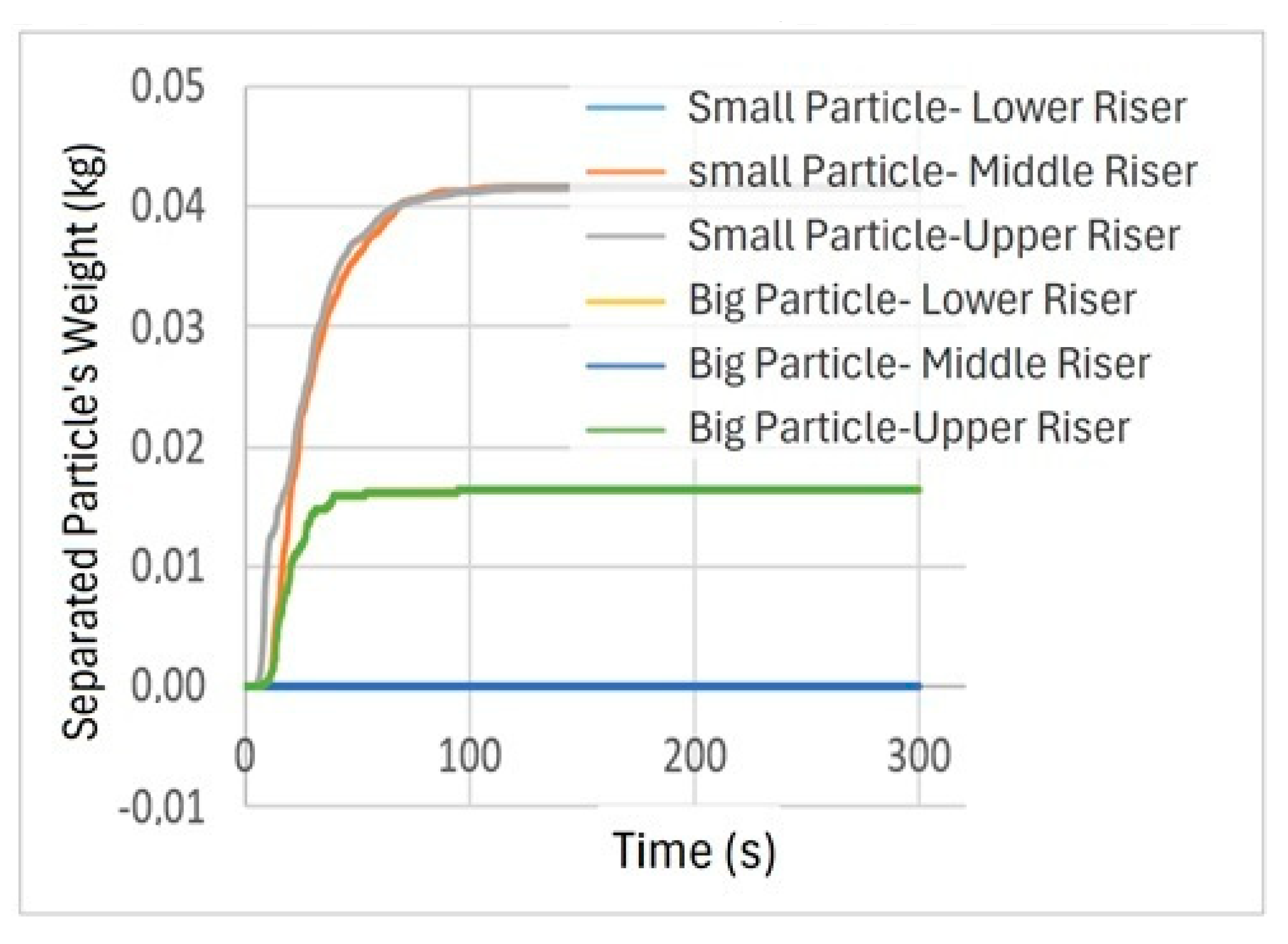
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mukherjee, A.K.; Mishra, B.K. Experimental and simulation studies on the role of fluid velocity during particle separation in a liquid-solid fluidized bed. Int. J. Miner. Process. 2007, 82, 211–221. [Google Scholar] [CrossRef]
- Rasul, M.G.; Rudolph, V.; Wang, F.Y. Particles separation using fluidization techniques. Int. J. Miner. Process. 2000, 60, 163–179. [Google Scholar] [CrossRef]
- Basu, P. Circulating Fluidized Bed Boilers Design, Operations, and Maintenance; Springer: Halifax, NS, Canada, 2015; pp. 143–144. [Google Scholar]
- Geldart, D. Types of gas fluidization. Powder Technol. 1973, 7, 285–292. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Progress 1952, 48, 9–94. [Google Scholar]
- Kunii, D.; Levenspiel, O. Fluidization Engineering, 2nd ed; Butterworth-Heinemann: Oxford, UK, 1991; pp. 155–164. [Google Scholar]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. I. The Basic Experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Snider, D.M. An incompressible three dimensional multiphase particle-incell model for dense particle flows. J. Comput. Phys. 2001, 170, 523–549. [Google Scholar] [CrossRef]
- Anderson, T.B.; Jackson, R. A fluid mechanical description of fluidized beds. Ind. Eng. Chem. Fund. 1967, 6, 527–539. [Google Scholar] [CrossRef]
- O’Rourke, P.J.; Zhao, P.; Snider, D. A model for collisional exchange in gas/liquid/solid fluidized beds. Chem. Eng. Sci. 2009, 64, 1784–1797. [Google Scholar] [CrossRef]
- Wen, C.Y. Mechanics of fluidization. Fluid Part. Technol. Chem. Eng. Progress. Symp. Ser. 1966, 62, 100–111. [Google Scholar]
- Anam, A.C.; Ikhwan, N. Experimental study of particle separation using fluidised bed method. In AIP Conference Proceedings, Proceedings of the THERMOFLUID X: 10th International Conference on Thermofluids 2019, Yogyakarta, Indonesia, 5 November 2019; AIP Publishing: Melville, NY, USA, 2019. [Google Scholar] [CrossRef]
- Pusat Penelitian Kelapa Sawit (PPKS), Biodiesel Minyak Sawit. Available online: https://iopri.co.id/product/detail/biodiesel-minyak-sawit (accessed on 15 September 2022).




| Name | Particle A (Small) | Particle B (Big) |
|---|---|---|
| Diameter (mm) | 0.9 (Blue) | 3 (Red) |
| Particle density (kg/m3) [13] | 1217.13 | 1217.13 |
| Fluid density (kg/m3) [12] | 837.5 | 837.5 |
| Fluid viscosity (kg/m-s) [12] | 2.72 × 10–4 | 2.72 × 10–4 |
| Particle zone [5] | Sand-like | Spout able |
| Minimum fluidization velocity (m/s) [6] | 6.7 × 10–4 | 6.8 × 10–3 |
| Terminal velocity (m/s) [5] | 3.6 × 10–2 | 0.132 |
| Fluid Velocity (m/s) | Riser Height (m) | Particle Size (mm) | Experiment Result for Extracted Particle (kg) | Simulation Result for Extracted Particle (kg) |
|---|---|---|---|---|
| 0.034 | 0.3 | 0.9 | 0.002434 | 0 |
| 3 | 0 | 0 | ||
| 0.6 | 0.9 | 0 | 0 | |
| 3 | 0 | 0 | ||
| 0.9 | 0.9 | 0 | 0 | |
| 3 | 0 | 0 | ||
| 0.068 | 0.3 | 0.9 | 0.048685 | 0.041531 |
| 3 | 0.002434 | 0 | ||
| 0.6 | 0.9 | 0.019474 | 0.040514 | |
| 3 | 0 | 0 | ||
| 0.9 | 0.9 | 0.014606 | 0.35467 | |
| 3 | 0 | 0 | ||
| 0.102 | 0.3 | 0.9 | 0.074245 | 0.041531 |
| 3 | 0.0718810 | 0.01643 | ||
| 0.6 | 0.9 | 0.060856 | 0.040917 | |
| 3 | 0 | 0.000354 | ||
| 0.9 | 0.9 | 0.046251 | 0.040536 | |
| 3 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amin, M.L.; Ikhwan, N. Numerical Simulation for Dual Solid Particle Separation Using Fluidized Bed. Eng. Proc. 2025, 84, 97. https://doi.org/10.3390/engproc2025084097
Amin ML, Ikhwan N. Numerical Simulation for Dual Solid Particle Separation Using Fluidized Bed. Engineering Proceedings. 2025; 84(1):97. https://doi.org/10.3390/engproc2025084097
Chicago/Turabian StyleAmin, Muhammad Lutfil, and Nur Ikhwan. 2025. "Numerical Simulation for Dual Solid Particle Separation Using Fluidized Bed" Engineering Proceedings 84, no. 1: 97. https://doi.org/10.3390/engproc2025084097
APA StyleAmin, M. L., & Ikhwan, N. (2025). Numerical Simulation for Dual Solid Particle Separation Using Fluidized Bed. Engineering Proceedings, 84(1), 97. https://doi.org/10.3390/engproc2025084097






