Glucose Prediction with Long Short-Term Memory (LSTM) Models in Three Distinct Populations ^†

Abstract

Diabetes mellitus is a chronic metabolic disorder characterized by the dysregulation of blood glucose, which can lead to a range of serious health complications if not properly managed. Continuous glucose monitoring (CGM) is a cutting-edge technology that tracks glucose levels in real time, providing continuous and detailed information about glucose fluctuations throughout the day. The CGM data can be leveraged to train deep learning models forecasting blood glucose levels. Several deep learning-based glucose prediction models have been developed for diabetes populations, but their generalizability to other populations such as prediabetic individuals remains largely unknown. Prediabetes is a condition where blood glucose levels are higher than normal but not yet high enough to be classified as diabetes. It is a critical stage where intervention can prevent the progression to type 2 diabetes. To fill in the knowledge gap, we developed Long Short-Term Memory (LSTM) glucose prediction models tailored to three distinct populations: type 1 diabetes (T1D), type 2 diabetes (T2D), and prediabetic (PRED) individuals. We evaluated the internal and external validity of these models. The results showed that the model constructed with the prediabetic dataset demonstrated the best internal and external validity in predicting glucose levels across all three test sets, achieving a normalized RMSE (NRMSE) of 0.21 mg/dL, 0.11 mg/dL, and 0.25 mg/dL when tested on the prediabetic, T1D, and T2D test sets, respectively.

1. Introduction

Diabetes mellitus is a disease characterized by elevated blood glucose levels due to impaired insulin production or insulin resistance. It is broadly classified into two primary types: type 1 diabetes (T1D), an autoimmune condition resulting in the destruction of insulin producing β-cells in the pancreas, and type 2 diabetes (T2D), which is predominantly associated with insulin resistance. Another increasingly common condition is prediabetes (PRED), characterized by higher-than-normal blood glucose levels that are not yet high enough to be diagnosed as diabetes. Often a precursor to T2D and cardiovascular diseases, PRED serves as a critical warning and a time point for intervention. It is usually diagnosed through measurements of glycated hemoglobin (HbA1c) when it is at a value of 5.7–6.4% [1].

Continuous glucose monitoring (CGM) is a method for tracking blood glucose levels in real time, providing a view of glucose trends and fluctuations throughout the day and generating a large amount of data. These data can be utilized to uncover insights into glycemic dynamics and their relationship to other aspects of human physiology and behavior [2,3]. Deep learning (DL) has emerged as a powerful technique to predict glucose based on CGM data in individuals with diabetes and thus be able to generate more accurate predictions. Long Short-Term Memory (LSTM) is a popular DL algorithm that can work with sequential and long-term CGM data, identifying complex patterns and relationships within the data and providing real-time glucose predictions [4]. These models have been widely used in subjects with T1D to predict glucose levels. On the other hand, there are few studies related to glucose prediction in the prediabetes population, highlighting the need for more studies targeting this population. Acknowledging the differences in glycemic dynamics across T1D, T2D, and prediabetes, we developed three LSTM models for three distinct populations and investigated the internal and external validation of the developed models on datasets of T1D and T2D subjects.

2. Materials and Methods

2.1. Dataset

Three databases were used in this study. For individuals with T1D, the Ohio dataset contains data from 12 individuals, of whom 58.3% are women and the mean age is 50 years. They were undergoing treatment with Medtronic Enlite 530G or 630G insulin pump, sourced by Medtronic located in Brampton, ON, Canada [5]. There is no information about the HbA1c values of this T1D cohort. Data collection spanned over 8 weeks using Medtronic Enlite CGM sensors, produced by Medtronic located in Brampton, Canada. Blood glucose levels were measured every 5 min. The second dataset has time series of blood glucose readings from 100 individuals, of which 44% are women and the average age is 60.1 years, with T2D, who wore for 3 to 14 days a FreeStyle Libre sensor, manufactured by Abbott located in Lake County, IL, USA. Glucose data were automatically stored in the sensor every 15 min [4]. After removing duplicated data, 92 people were included in the T2D dataset for model training and testing. The last dataset contains information collected from 16 prediabetic subjects, of whom 56.2% are female, using for 10 days a Dexcom G6, developed by DEXCOM based on San Diego, CA, USA [1]. Glucose readings were recorded every 5 min. The average of HbA1c of the prediabetic cohort was 41.5 mmol/mol.

2.2. Model Development

The LSTM models were developed to predict the glucose level at time t + 1 based on the glucose level at time t. Before fitting the dataset, the glucose data were scaled using MinMaxScaler from the scikit-learn version 1.6.0 with Python 3.11.5. The LSTM models were built using the Keras (version 2.12.0) and have 128 LSTM units, followed by a dense layer (150 units), dropout layer (0.20), dense layer (100 units), dropout layer (0.15), dense layer (50 units), dense layer (20 units), and a final layer with one unit (for prediction). ReLU was used as the activation function with the Adam optimizer. The loss was calculated in mean squared error (MSE) and later converted into root mean squared error (RMSE). They were trained for 200 epochs with a batch size of 32. The models were tuned using 5-fold cross validation.

The three models were trained with data from the subjects with the greatest number of glucose records in each dataset, separated into T1D (3066), T2D (1328) and PRED (2846). For internal validation, each model was tested on the rest of the subjects in the correspondent dataset. For external validation, each model was tested on the different datasets.

2.3. Evaluation Measures

Mean absolute error (MAE), root mean squared error (RMSE), and normalized RMSE (NRMSE) were used to evaluate the models. Prior studies recommended NRMSE as a better metric over the other two, as it is useful for comparing models of different scales [6]. In this study, NRMSE was calculated as the RMSE normalized over the standard deviation of the true values of each dataset.

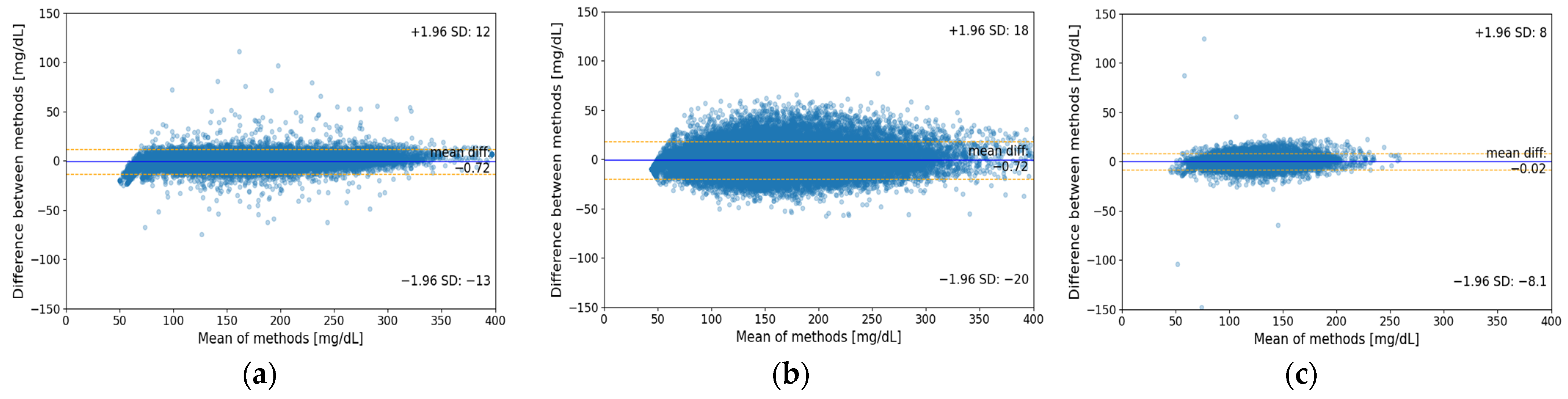
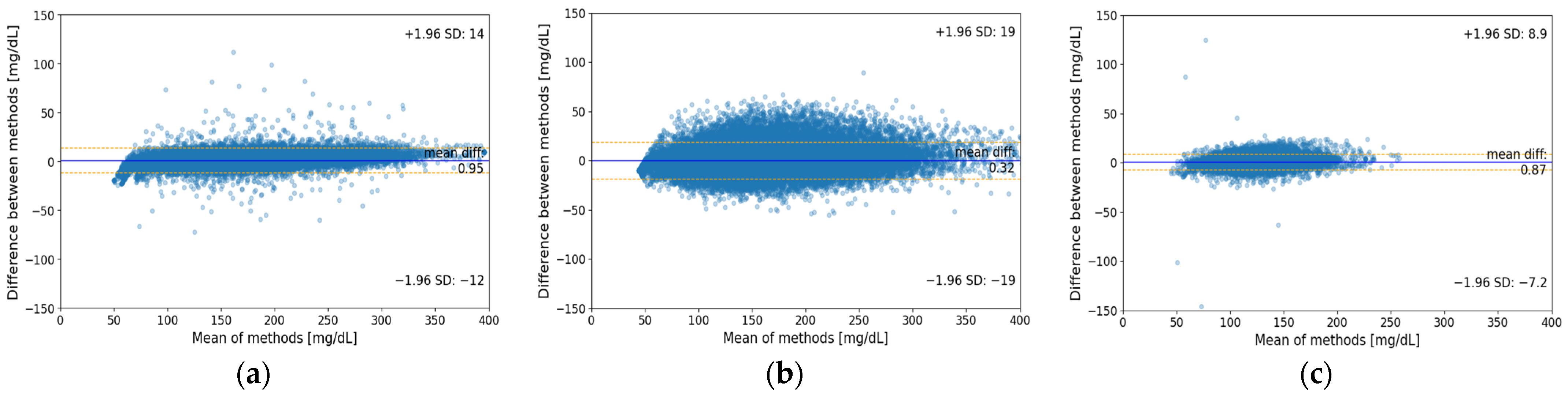
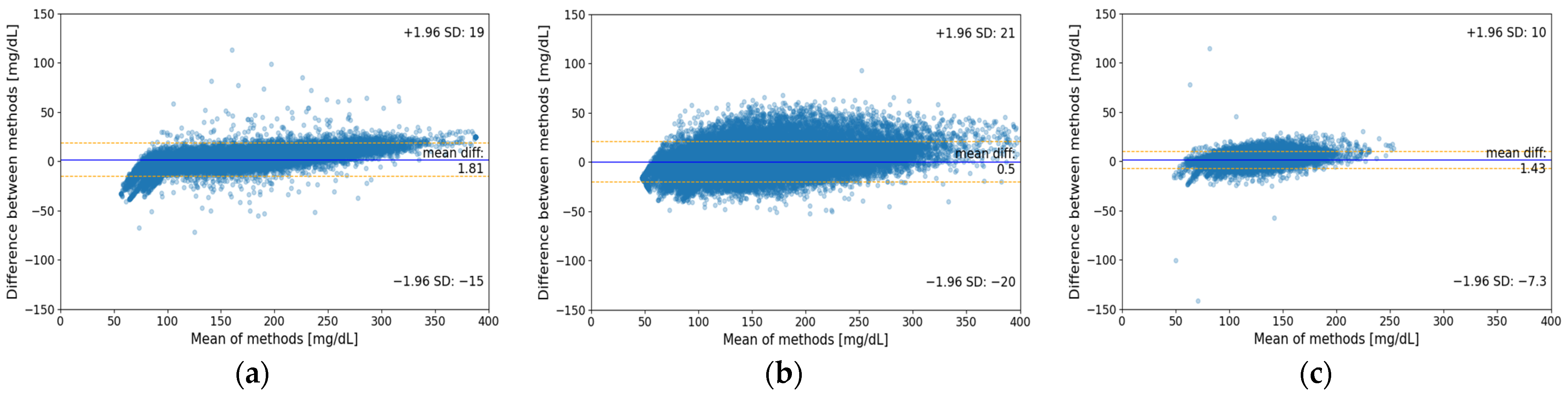
This study employed Bland–Altman (B&A) analysis to compare the differences between the true values and the model predictions. It plots the difference between the two measurements against their average. The B&A method quantifies the agreement between two quantitative measurements by analyzing the mean difference and establishing limits of agreement (LoA). These statistical limits are calculated by using the mean and the standard deviation of the differences between the two values. The plot offers a straightforward approach to detect any bias in the mean differences and to estimate an agreement interval, within which 95% of the differences between the two methods are expected to fall [7].

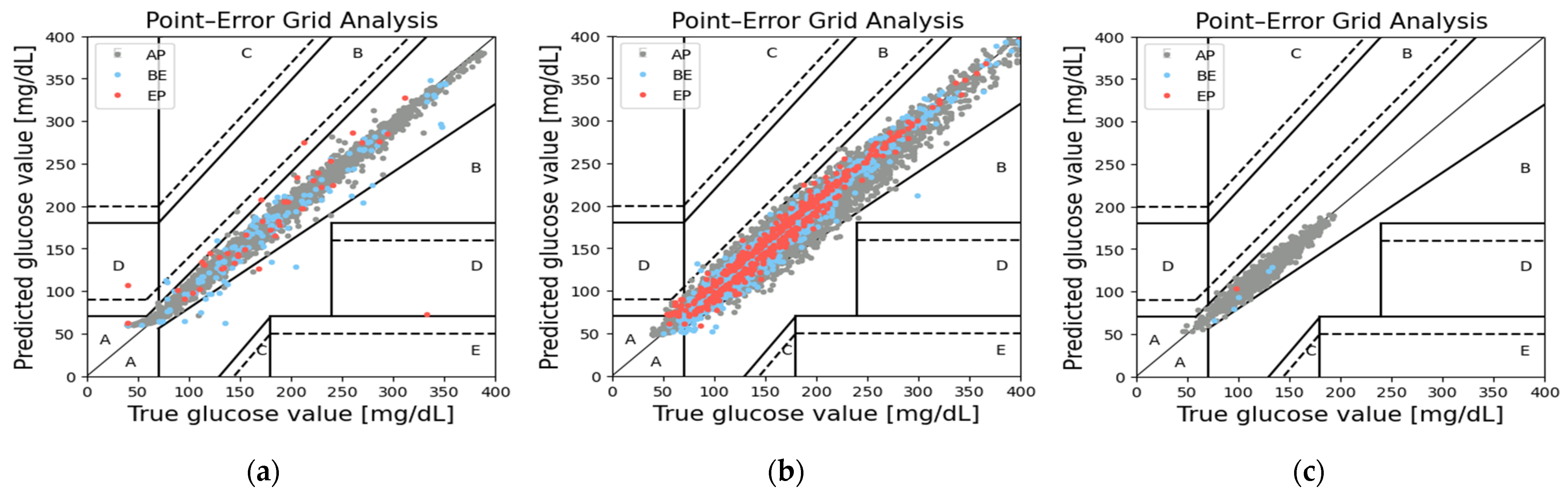
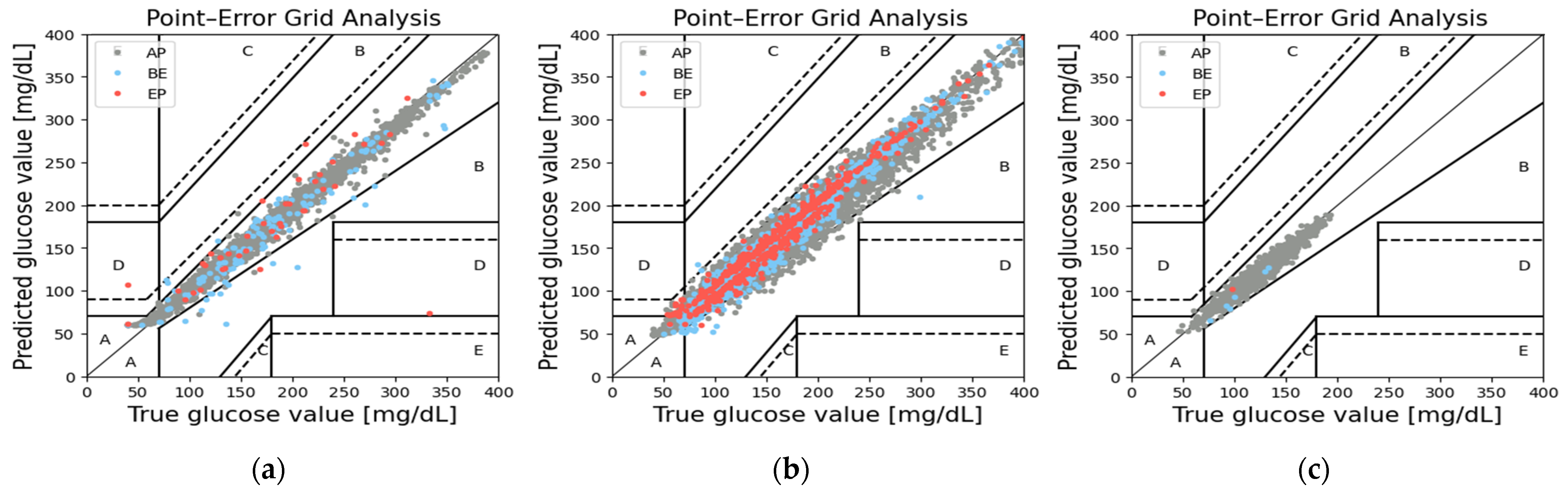
Continuous Glucose–Error Grid Analysis (CG-EGA) is a method of evaluating the accuracy of continuous glucose monitoring. It serves as an evolution of the original Error Grid Analysis (EGA), which was created to assess the clinical accuracy of blood glucose readings obtained through estimation or self-monitoring systems. CG-EGA operates on the principle that the data generated by a monitoring system should be reliable enough to support clinically accurate decision-making by the user. The CG-EGA graphic plots sensor blood glucose values (SBG) versus reference blood glucose (RBG) divided into A, B, C, D, and E zones. Zones A and B are usually considered to be clinically acceptable, and zones C to E are considered to be clinically significant errors.

3. Results

Table 1. Summary of metrics of all models.

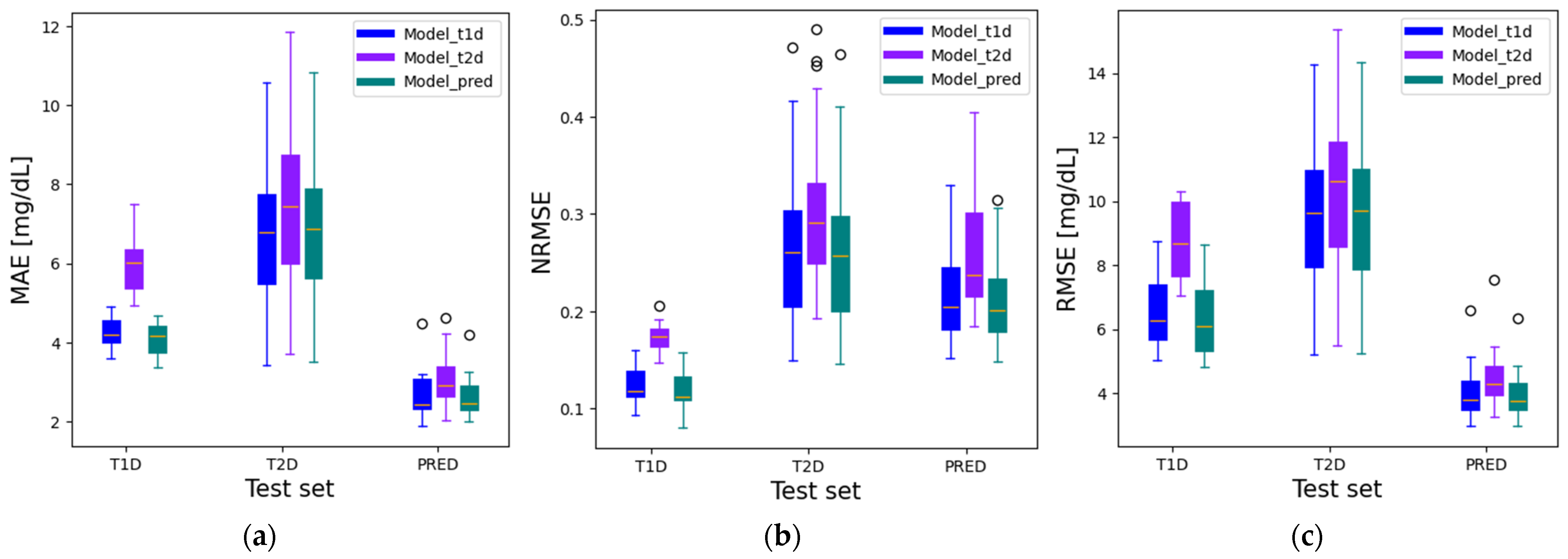
Model	Dataset	MAE	RMSE	NRMSE
	PRED	2.66 ± 0.54	4.00 ± 0.83	0.21 ± 0.04
LSTM_pred	T1D	4.07 ± 0.43	6.39 ± 1.25	0.11 ± 0.02
	T2D	6.83 ± 1.48	9.55 ± 2.06	0.25 ± 0.06
	PRED	2.70 ± 0.60	4.07 ± 0.88	0.22 ± 0.05
LSTM_t1d	T1D	4.24 ± 0.38	6.59 ± 1.17	0.12 ± 0.02
	T2D	6.70 ± 1.44	9.54 ± 2.04	0.25 ± 0.06
	PRED	3.11 ± 0.65	4.55 ± 0.96	0.26 ± 0.05
LSTM_t2d	T1D	5.97 ± 0.69	8.77 ± 1.18	0.17 ± 0.01
	T2D	7.45 ± 1.74	10.42 ± 2.27	0.29 ± 0.05

shows a summary of the mean and standard deviation of the performance achieved by the three LSTM models in internal and external tests. The results showed that the model LSTM_pred obtained better MAE and RMSE metrics compared to the others. We observed that the MAE and RMSE metrics were higher when the model was tested on the T2D dataset. This is due to the fact that the prediction window of this dataset is 15 min, which is longer than the 5 min prediction window in the other two test sets, thus causing larger errors. The NRMSE metric demonstrates lower values for the T1D test set, which can be attributed to the greater variability in glucose levels within this group. Our findings highlight significant differences in model performance when evaluated using different metrics.

Figure 1 illustrates the box-plots of all model metrics when tested on the three different datasets. The results corroborate those found in Table 1, showing the lowest values of the MAE and RMSE metrics for the prediabetic population, while NRSME presents a lower value for the T1D dataset. Analyzing the graphs, we observe the large dispersion of errors for the T2D dataset, which is likely due to its large number of subjects.

3.1. Bland–Altman Plots

Figure 2, Figure 3 and Figure 4 represent the B&A plots for the models applied in all test sets. We observe that the majority of data points are within the upper and lower limits of agreement (LoA), which are represented by the yellow dotted lines, and are centered around the average in all B&A plots. No systematic bias was detected in any of the models. In addition, the graphs related to the T2D subjects demonstrate a larger standard deviation and consequently a larger LoA compared to all others, which can be explained by this dataset being recorded at 15 min intervals, while the other datasets are recorded at 5 min intervals. In addition, this dataset has the largest number of individuals (N = 92).

Table 2. Summary of Bland–Altman results of all models.

Model	Dataset	Mean Differences	+1.96 DP	−1.96 DP
	PRED	0.02	8.0	−8.1
LSTM_pred	T1D	−0.72	12.0	−13.0
	T2D	−0.72	18.0	−18.1
	PRED	0.87	8.9	−7.2
LSTM_t1d	T1D	0.95	14.0	−12.0
	T2D	0.32	19.0	−19.0
	PRED	1.43	10.0	−7.3
LSTM_t2d	T1D	1.81	19.0	−15.0
	T2D	0.50	21.0	−21.0

shows a summary of all values of the models and Model_pred obtained the best results, as indicated by the narrowest LoA, especially when the test set was subjects with prediabetes (+8 and −8 mg/dL).

3.2. Continuous Glucose–Error Grid Analysis—CG-EGA

Table 3. Summary of CG-EGA of all models.

Model	Dataset	AP	BE	EP
	PRED	99.8%	0.15%	0.15%
LSTM_pred	T1D	99.6%	2.50%	0.90%
	T2D	89.9%	7.20%	2.80%
	PRED	99.8%	0.14%	0.06%
LSTM_t1d	T1D	96.8%	2.39%	0.81%
	T2D	89.9%	7.22%	2.81%
	PRED	99.7%	0.15%	0.10%
LSTM_t2d	T1D	95.3%	2.34%	2.36%
	T2D	89.9%	7.52%	2.50%

shows information from the analysis of the Continuous Glucose–Error Grid Analysis (CG-EGA) graphs of all models when validated on the three test sets. Figure 5, Figure 6 and Figure 7 present the EGA plots for the models applied to the three datasets. The graphics are divided into A, B, C, D and E regions, represented by the solid lines. The dashed lines represent the expansion of the limits in zones A, B, and D, if the rate of true glucose level is 1 to 2 mg/dL.min.

The CG-EGA results indicate that none of the three models achieved good clinical accuracy on the T2D dataset. Model_pred achieved the highest values in the AP region when validated on the prediabetic test set and reasonably good AP when validated on the T1D and T2D test sets. As shown in Table 3, this pattern manifests again for Model_t1d and Model_t2d. The compromised performance of all three models may be explained by the longer records interval of the T2D dataset (i.e., 15 min) compared to the other two datasets. The T2D dataset also has a much larger number of individuals, potentially leading to more prediction errors, which may in turn result in wrong clinical decisions.

4. Discussion

4.1. Principal Findings

Most existing deep learning-based glucose prediction models have only undergone internal validation, leaving the generalizability of the models to other populations unclear. In this study, we trained three different models with different types of diabetes conditions (T1D, T2D, and PRED) and performed both internal and external validation.

4.2. Comparison with Prior Studies

Numerous studies have endeavored to build deep learning models for predicting glucose levels in the diabetic population. Models such as LSTM were used in the BGLP Challenge in 2020, using the OhioT1DM dataset to forecast glucose values. Bhimireddy et al. used DL models to forecast glucose level at a 30 min horizon; the LSTM model achieved an average RMSE value of 25.0 mg/dL [8]. LSTM-type models were also used by [9], being tested on T1D subjects. They achieved an MAE of 19.4 mg/dL and an average RMSE of 14.1 mg/dL. A novel multivariate predictor with a multi-scale LSTM was used to predict the glucose of T1D subjects through 30 min and 60 min [10]. The RMSE values of 30 min and 60 min predictions were 19.0 and 32.0 mg/dL, respectively, and the MAE values of 30 min and 60 min predictions were 13.5 and 23.8 mg/dL. In addition, Butt et al. [11] developed a multi-layered LSTM-based recurrent neural network for a forecasting horizon of 30 and 60 min. The model achieved the lowest RMSE score of 14.76 mg/dL and 25.48 mg/dL for prediction horizons of 30 and 60 min, respectively. Research effort has also been made to improve the interpretability of LSTM-type glucose prediction models. The researchers of [12] developed personalized bidirectional LSTM equipped with a tool that enables its interpretability. Their algorithm was able to preserve the physiological meaning of the considered inputs and achieved an RMSE of 20.20 mg/dL and an MAE of 14.74 mg/dL for 30 min prediction. In comparison to these existing models, all our three models obtained better results regarding MAE and RMSE. However, it is worth noting that our work differs from prior studies regarding the prediction horizon. While most existing models were developed for 30 or 60 min horizons, our models were developed for a much shorter horizon of 5 or 15 min, depending on the dataset adopted.

4.3. Limitations and Future Work

The present study has several limitations. The first limitation is the sizes of the datasets. For example, the T1D dataset consists of only 12 participants, while the PRED dataset only has 16 participants. The granularity of demographic information also varies across the datasets used, with the T1D and PRED datasets only containing an age range rather than the specific age of the participants. The data quality imposes another potential limitation, particularly regarding the sampling rate of the glucose levels. While the T2D data were recorded every 15 min, the T1D and PRED groups were recording every 5 min. This difference may have produced distorted performance when the models were tested on the T2D dataset. In our future work, we will attempt to use other types of deep learning algorithms, as well as utilizing larger datasets with diverse demographics. We also plan to incorporate other types of signals in addition to historical glucose data into the model construction.