This section outlines the comprehensive methodology utilised in this study to optimise flight paths for a two-aircraft formation on the Melbourne to Sydney city-pair route, focusing on conflict avoidance and fuel efficiency. The methodology is divided into macroscopic and microscopic levels to address the strategic and detailed flight optimisation aspects. At the macroscopic level, overall planning and coordination are emphasised, including route optimisation, formation flight planning, ATM integration, environmental impact, and leader aircraft conflict avoidance. At the microscopic level, adjustments to individual followers’ aircraft flight profiles are made to ensure minimum separation and flight safety and efficiency during the cruise phase. The optimisation algorithm iteratively adjusts parameters such as positions, speeds, and waypoints to minimise the weighted sum of fuel consumption and travel time while maintaining minimum horizontal and vertical separation distances. The mathematical formulation of the problem involves a gradient-based optimisation algorithm applied to a constrained nonlinear multivariable function. Detailed pseudocode for the optimisation algorithm is provided offering a clear procedural framework for implementing the proposed solution.
3.1. Concept and Framework
3.1.1. Macroscopic Level
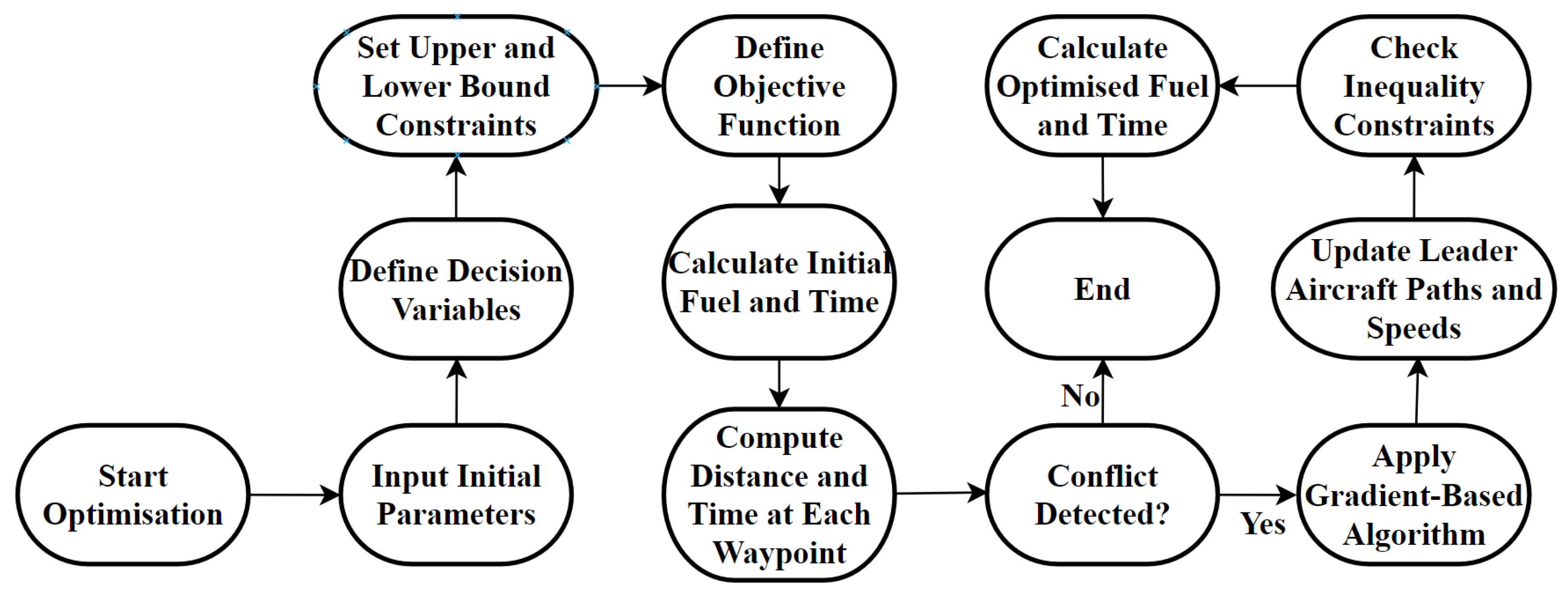
The macroscopic level displayed in
Figure 1 involves the overall planning and coordination of two-aircraft information on the Melbourne to Sydney city-pair route and designated airspaces. It includes strategic decision-making for optimising flight routes, ensuring safety and efficiency, and minimising fuel consumption across the entire network. The optimisation process begins with initialising the necessary parameters, including the initial positions, waypoints, and speeds for both aircraft. The initial lateral and vertical distances between the aircraft at each waypoint are then computed to check for any potential conflicts. If no conflicts are detected, the process proceeds without adjustment. However, if a conflict is detected, the optimisation process is triggered. The optimisation process involves setting up constraints by defining the bounds for the decision variables and the lateral and vertical separation requirements. An objective function is then established to minimise both the fuel consumption and travel time. The gradient-based algorithm is applied to optimise the path of the leader aircraft within these constraints. The waypoints and speeds are adjusted based on the optimised results, and the new paths are verified to ensure they satisfy all constraints. Finally, the optimised paths are finalised, and the total fuel consumption and travel time are calculated, marking the end of the optimisation process.
The key elements considered at the macroscopic level include:
1. Route Optimisation: Identifying the most efficient flight paths for aircraft formation, taking into account air traffic, restricted airspaces, and weather conditions.
2. Formation Flight Planning: Determining the optimal positions and coordination strategies for the aircraft to maximise aerodynamic benefits and reduce overall fuel consumption.
3. Air Traffic Management (ATM) Integration: Incorporating air traffic controller (ATC) advisories and constraints to ensure compliance with regulations and coordination with other air traffic.
4. Environmental Impact: Minimising emissions by optimising the flight paths.
5. Conflict Avoidance: Ensuring that the formation maintains safe separation from other aircraft throughout the flight.
3.1.2. Microscopic Level
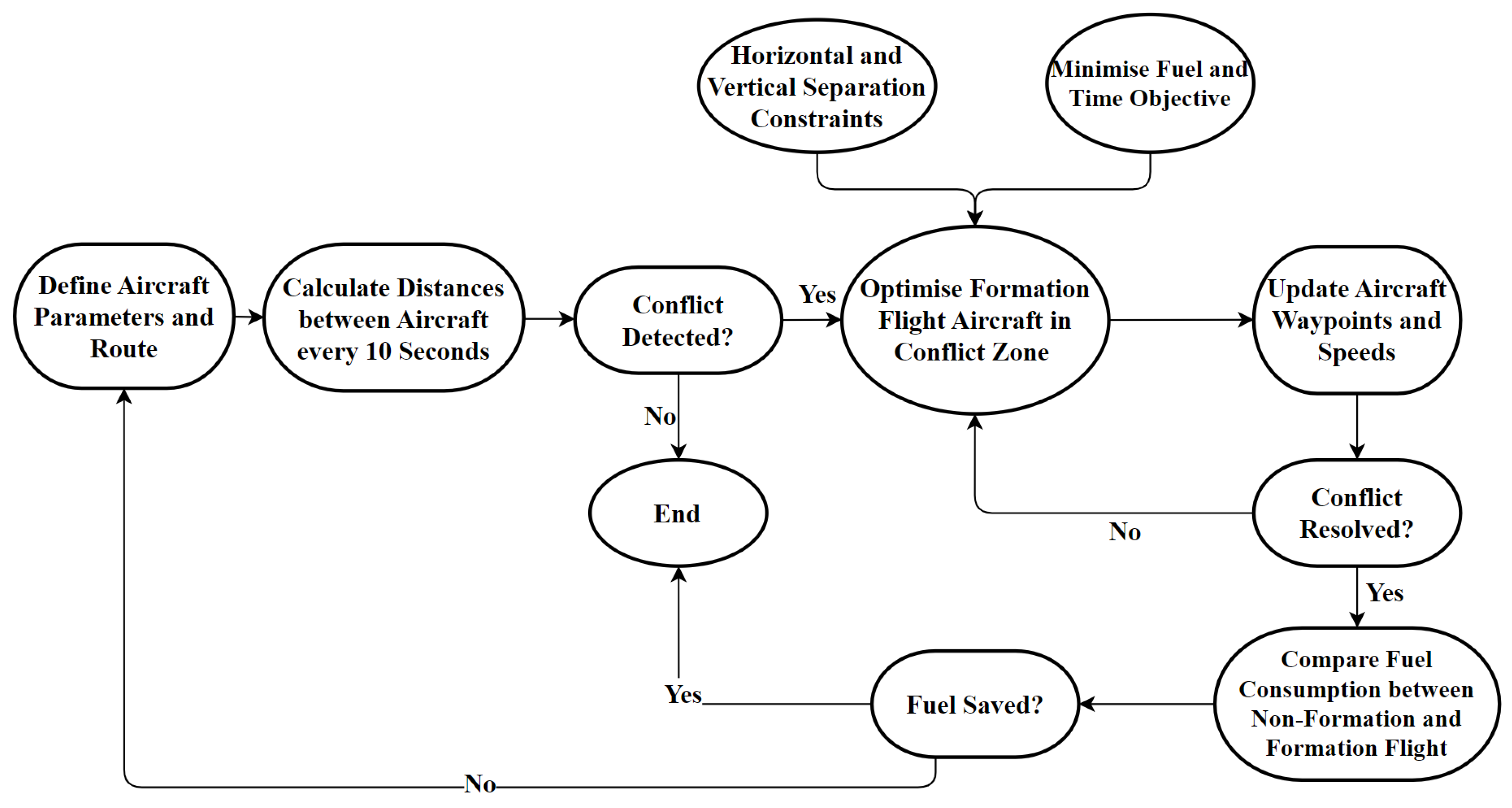
The microscopic level displayed in
Figure 2 focuses on the detailed optimisation of the individual aircraft flight profiles. This involves real-time adjustments to altitude, heading, and speed to ensure safety (conflict avoidance) and efficiency (fuel savings) during different phases of flight (take-off, cruise, and landing). The key elements considered at the microscopic level include:
1. Flight Profile Adjustments: Dynamic changes to the altitude, heading and speed based on real-time data to maintain optimal formation and avoid conflicts.
2. Aerodynamic Interactions: Analysing the aerodynamic benefits of formation flight, such as reduced drag and fuel consumption, and path planning to maximise these benefits.
3. Separation Management: Maintaining both lateral and vertical separation to ensure safety, especially during manoeuvers and in response to potential conflicts.
Figure 2.
Microscopic level flowchart.
Figure 2.
Microscopic level flowchart.
3.2. Problem Mathematical Formulation
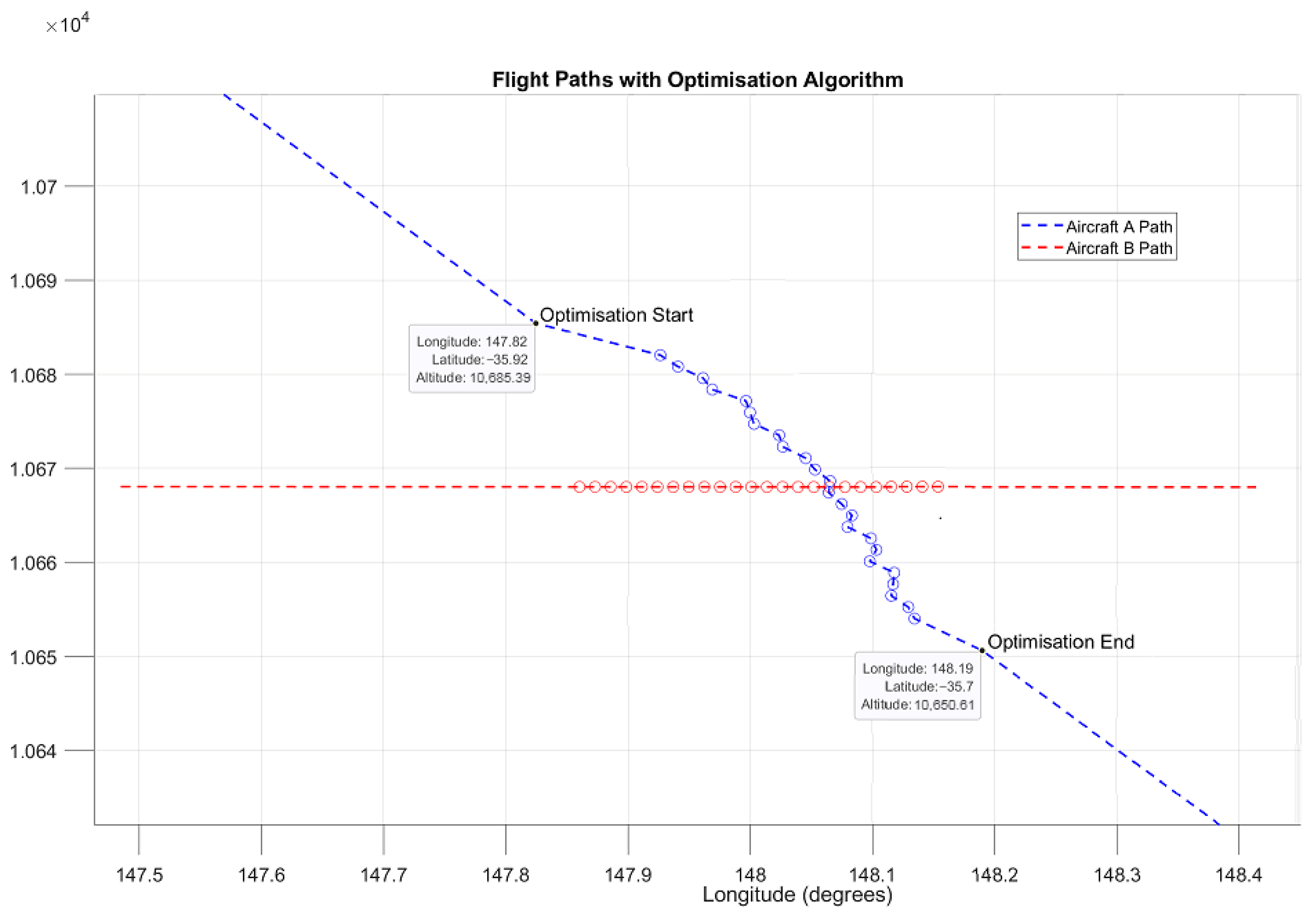
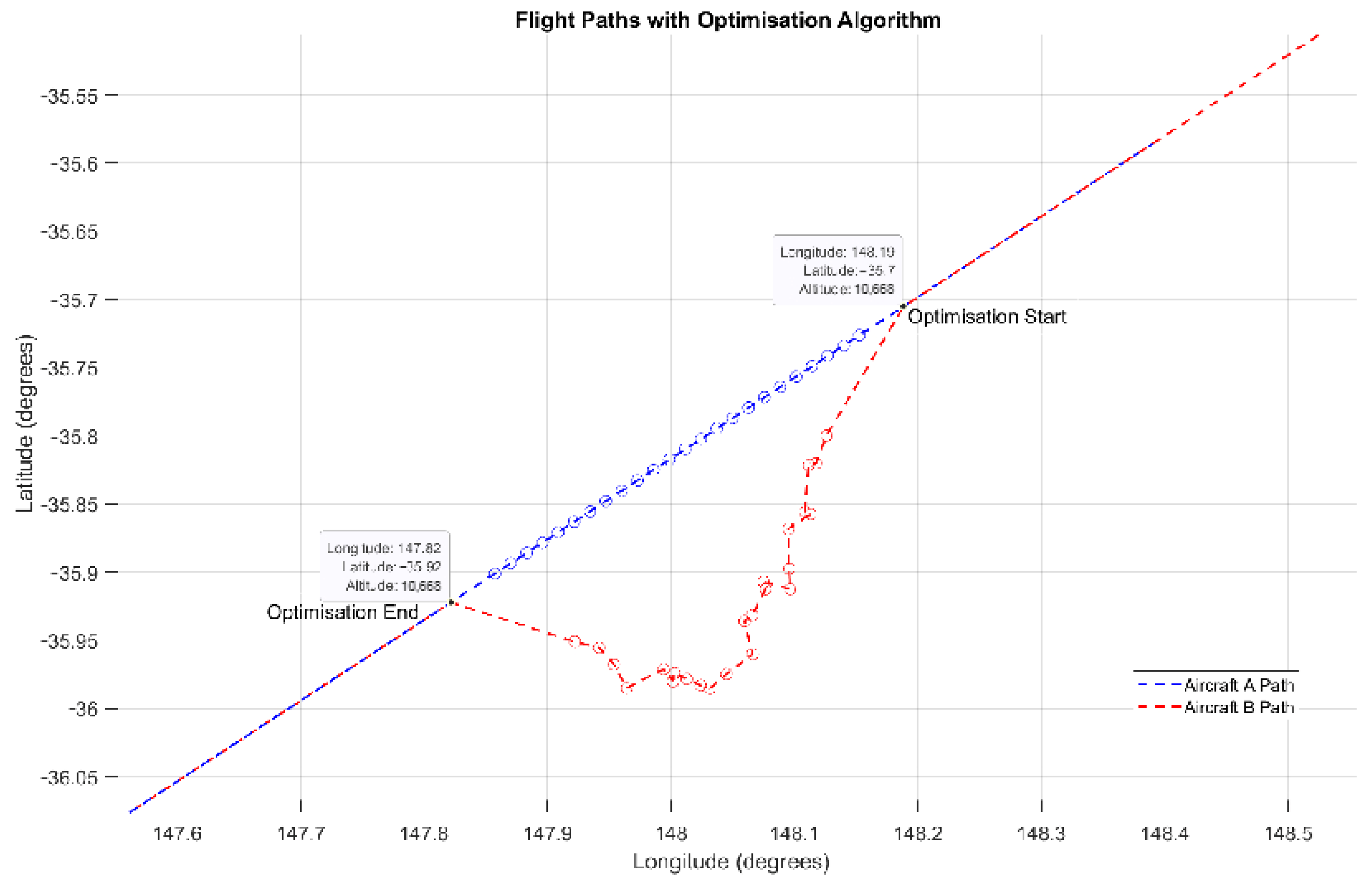
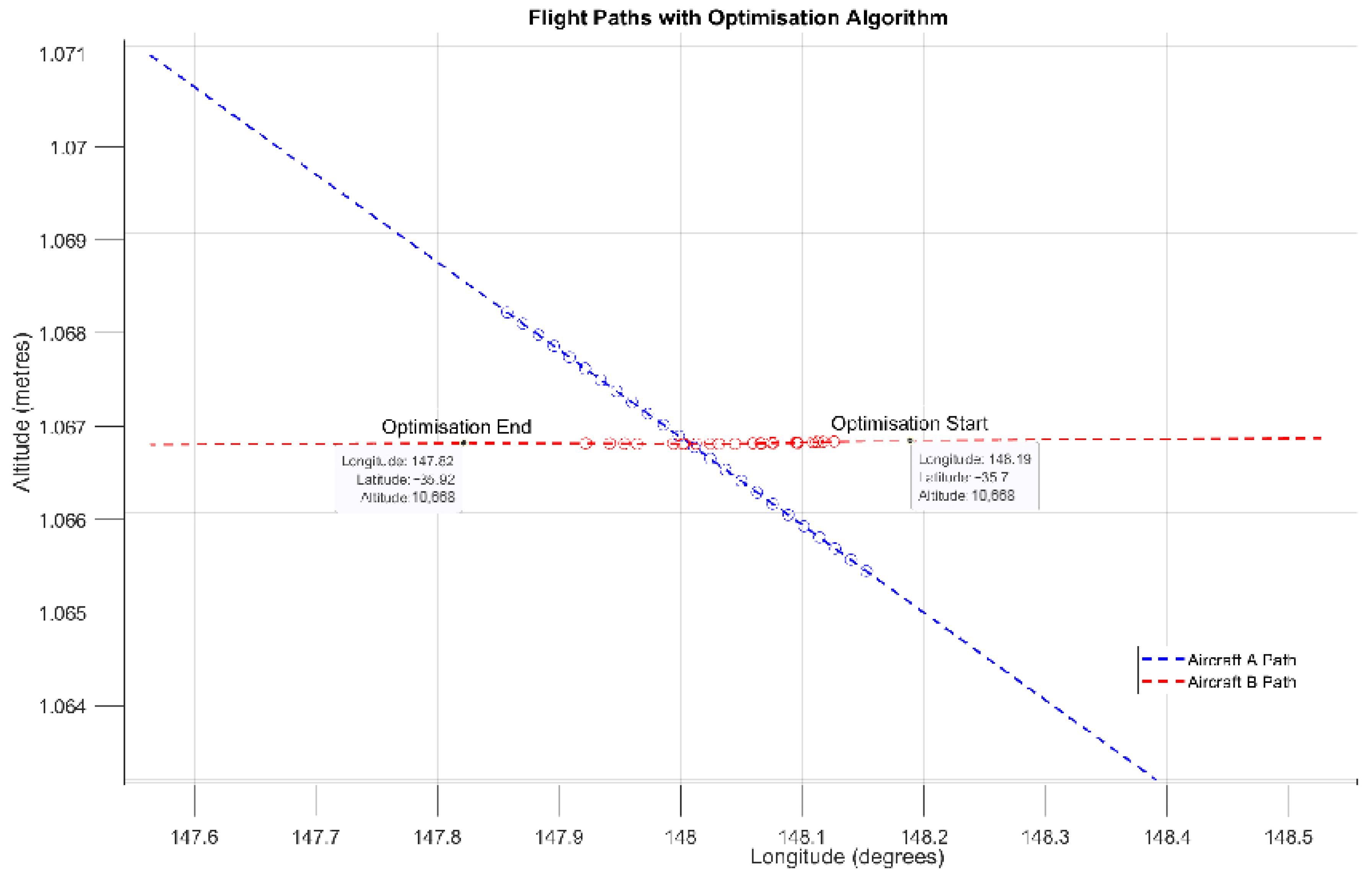
The mathematical problem involves optimising the fuel consumption of a two-aircraft formation that encounters a conflict with another two-aircraft formation during the cruise phase. The optimisation is carried out using a gradient-based algorithm applied to a constrained nonlinear multivariable function. The objective is to minimise fuel consumption for Melbourne to Sydney’s busy short-haul city-pair route whilst adhering to the lateral and vertical separation requirements for conflict avoidance. By performing an analysis and optimisation of the ‘leader’ aircraft fuel consumption, it is assumed that the ‘follower’ aircraft in the formation has the same behaviour; furthermore, it is assumed that the follower aircraft keeps a safe distance from the leader aircraft at all times.
The optimisation problem can be stated as:
Subject to the lower and upper bounds:
And separation constraints:
Vector of inequality constraints: .
Vector of equality constraints: .
There are
i number of flights; in this case, there are two leader aircraft in the simulation, denoted as aircraft ‘A’ and aircraft ‘B’, respectively:
and are the initial and final waypoints of aircraft A.
and are the initial and final waypoints of aircraft B.
n is the number of waypoints between the start and end points.
For n number of waypoints, the distance between each leader aircraft is checked every 10 s along the route. The distance
between waypoints
and
, at time t = 10 s is calculated:
where
and
t is the time interval (10 s).
The aircraft begins at
and
, the distance
is calculated at each waypoint every 10 s, and this is continued until reaching the final waypoints
and
. A conflict is detected when
is less than or equal to the minimum horizontal separation distance
:
The ‘conflict zone’ is defined by a sphere with a radius .
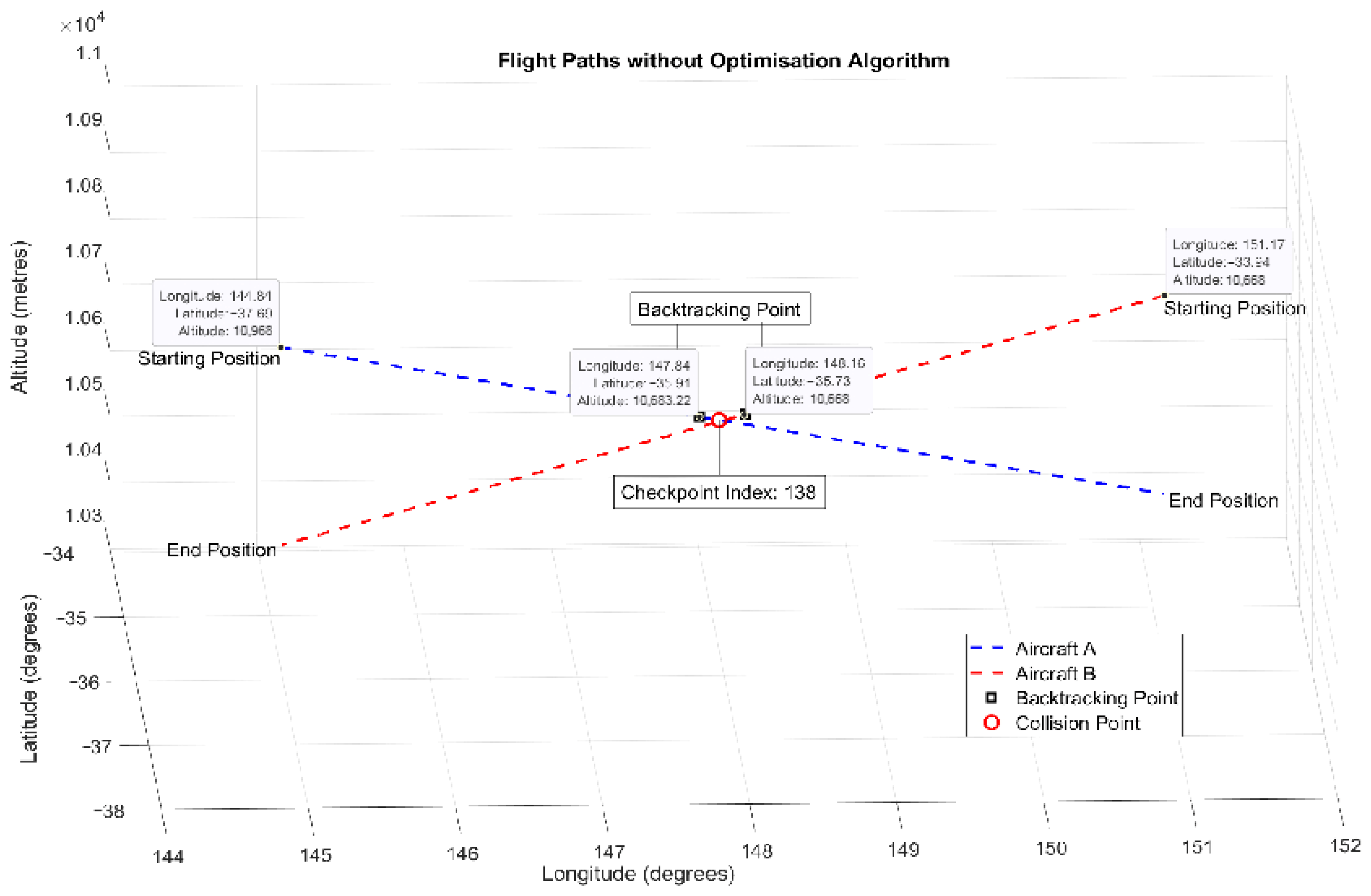
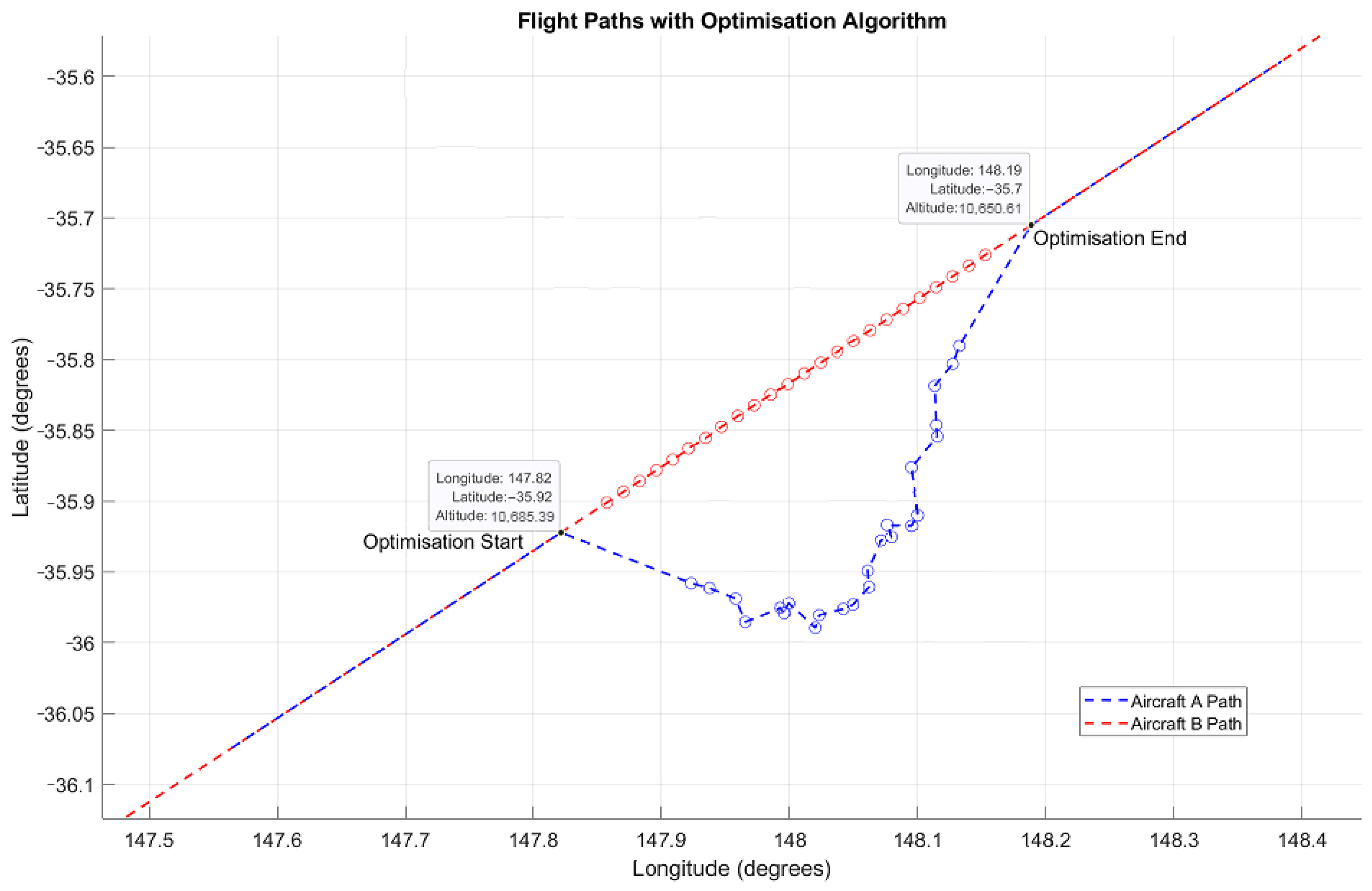
When a conflict is detected () a gradient-based algorithm is applied to optimise the route of one leader aircraft within the ‘conflict zone to avoid collision with the other leader aircraft. The optimiser must resolve the conflict within 120 s, reflecting an estimate of real-world air traffic control (ATC) decision-making time.
3.2.1. Objective Function
The objective of the mission optimisation is to minimise both the fuel burn and time of the leader aircraft. The optimisation algorithm utilises a weighted objective function with the three following variables: range , speed , and waypoint position.
Decision Variables
For
i flights with n waypoints each, the decision variables can be represented as:
Aircraft Range
The range of each leader aircraft is constrained to remain within the conflict zone, defined by the detected point of conflict . The conflict zone is bounded by a time window of ±60 s from the time of conflict detection .
This time window is defined as:
The range
of the leader aircraft within the conflict zone must be within the bounds defined by the time window. Let
be the position of the conflict point at the time
:
where
are the longitude, latitude, and altitude of the conflict point
. Change x, y, and z to long, lat, and alt.
The range
of the leader aircraft at any time
t within the conflict zone is constrained by:
This constraint ensures that the range of the leader aircraft remains within the conflict zone, allowing for an effective resolution of potential conflicts within the specified time window.
Aircraft Speed
The initial speed of each leader aircraft is defined as
; however, the optimiser may adjust the speed of the aircraft conflicts within the upper and lower bounds in the conflict zone to avoid conflicts. The speed is constrained within the following bounds:
where
and
.
Aircraft Waypoints
For the i number of flights, the waypoints are a set of coordinates (longitude, latitude, and altitude) that define the path of each leader aircraft inside the conflict zone.
Inside the conflict zone, the number of waypoints
n = 24 for each flight, and the waypoints for flight
i of the
k number of flights can be represented as:
where
are the longitude, latitude, and altitude of the
j-th waypoint for flight
i of the
k number of flights. The lower and upper bounds for
are defined as:
where
and
where
and
where
and
.
The concatenated lower-bound vector
lb and upper-bound vector
ub for flight
i of the
k number of flights are:
Weights of the Objective Function
The weights of the objective functions are defined as
3.2.2. Fuel Consumption and Time Calculation
The fuel consumption and time for each flight are calculated using a detailed simulation of the aircraft’s flight path with the following aircraft specifications:
S: Wing Area (m2)
CDo: Base drag coefficient
E: Oswald efficiency factor
AR: Aspect ratio
SFC: Specific fuel consumption (kg/s/N)
g: Acceleration due to gravity (m/s2)
M: Aircraft initial mass (kg)
K: Number of subsegments per segment
p: The air density based on altitude (kg/m3)
Path and Speed
The flight path is divided into segments, where the speed of the aircraft is calculated at each segment.
Loop over each Segment
For each segment of the flight path, the following steps are performed:
1. Calculate the segment distance using the latitude and longitude of the waypoints;
2. Determine the time to travel the segment using the speed;
3. Subdivide the segment into K subsegments for detailed calculation.
For each subsegment:
- -
Calculate the lift coefficient , drag coefficient , and thrust ;
- -
Compute the fuel flow rate and update the fuel consumption;
- -
Update the mass of the aircraft after fuel consumption.
Total Fuel and Time
- -
The total fuel consumption () is the sum of the fuel consumed over all segments;
- -
The total time () is the total distance divided by the speed.
The fuel consumption (
:
The total cost is the weighted sum of fuel and time:
3.2.3. Aircraft Separation Constraints
The separation constraints ensure that the leader aircraft maintain a minimum lateral and vertical separation distance from each other at all times during their flight paths in the conflict zone. These constraints are critical to avoid collisions.
The inequality constraints are based on the lateral and vertical distances, where the vector of inequality constraints is .
Inside the conflict zone, the number of waypoints
n = 24 for each flight, and the waypoints for flight
i of the
k number of flights can be represented as:
where
are the longitude, latitude, and altitude of the
j-th waypoint for flight
i of the
k number of flights.
The relative distance
between flights A and B is calculated by:
where
i and
k are the indices for the two different leader aircraft, and
j is the waypoint index.
The minimum horizontal separation is 9260 metres, and the minimum vertical separation is 300 metres.
Horizontal Distance Constraints
Vertical Distance Constraints
By structuring the constraints in this manner, it is ensured that the leader aircraft maintain the required lateral and vertical separation distances throughout their flight paths in the conflict zone, thus avoiding collisions.