Information-Theoretic Security of RIS-Aided MISO System Under N-Wave with Diffuse Power Fading Model ^†

Abstract

This paper aims to examine the physical layer security (PLS) performance of a reconfigurable intelligent surface (RIS)-aided wiretap multiple-input single-output (MISO) system over generalized fading conditions by assuming inherent phase shift errors at the RIS. Specifically, the procedures (i.e., the method) to conduct this research is based on learning-based approaches to model the magnitude of the end-to-end RIS channel, i.e., employing an unsupervised expectation-maximization (EM) approach via a finite mixture of Nakagami-m distributions. This general framework allows us to accurately approximate key practical factors in RIS’s channel modeling, such as generalized fading conditions, spatial correlation, discrete phase shift, beamforming, and the presence of direct and indirect links. For the numerical results, the secrecy outage probability, the average secrecy rate, and the average secrecy loss under different setups of RIS-aided wireless systems are assessed by varying the fading parameters of the N-wave with a diffuse power fading channel model. The results show that the correlation between RIS elements and unfavorable channel conditions (e.g., Rayleigh) affect secrecy performance. Likewise, it was confirmed that the use of a RIS is not essential when there is a solid line-of-sight link between the transmitter and the legitimate receiver.

1. Introduction

Recently, RISs have received academic and industrial attention for their promising potential to customize the wireless channel cost-effectively. A RIS element can be programmed to adjust the phases, amplitude, phase frequency, and even the polarization of the impinging signal on the RIS to overwhelm the hazardous consequences of the channel. Owing to the promising RIS’s features, this technology will presumably permit PLS to finally advance as a defense technique for delivering information security to wireless systems by exploiting the wireless propagation’s intrinsic randomness (e.g., fading and noise). Motivated by these reasons, some research works on RIS-aided secure systems under diverse fading channel conditions have been studied in the literature [1]. Nevertheless, an in-depth examination of RIS-related studies in PLS indicates that the typical premise is to consider Rayleigh fading to model the individual end-to-end RIS channels for the mathematical facility. However, the original intention of RIS is to provide reliable line-of-sight (LoS) links between the indirect RIS channels. Therefore, unlike the Rayleigh model, the generalized channel models are better suited to deliver these requirements thanks to their freedom to model different propagation environments. In recent years, some activities have been addressed to develop a more precise channel model through two procedures: On the one hand, envelope-aided fading models, such us [2]. On the other hand, ray-based channel models where the received wave is constructed from dominant specular components plus several scattered waves with random phases [3]. The pioneering ray-based model was proposed in [4] and called the N-wave with diffuse power (N-WDP) model. This type of channel model is suited to accommodate different wireless channel conditions encountered in upcoming networks for higher frequencies. Particularly, the N-WDP models have exhibited satisfactory exactness in characterizing the short-fading channel in mm wave bands [5]. Regarding the performance of the RIS over different fading channel models, in [6], the authors developed a unified framework to assess the outage performance of RIS-assisted communications over generalized fading channels in the presence of phase error noise by using Fox’s H functions. Likewise, in [7], a comprehensive statistical, secrecy, and performance analysis of RIS-assisted multiple-antenna systems under Weibull fading was presented. In [8], the secrecy rate analysis for a RIS-aided multi-user MISO system over a Rician fading channel was explored. Recently, in [9], the secrecy performance of RIS-aided systems over the Rician channel by assuming spatially random eavesdroppers was analyzed.

In light of the aforementioned points, and encouraged by the RIS features, this paper investigates how more realistic fading channels, discrete phase shifts, and spatial correlation impact the secrecy performance of RIS-assisted networks. Specifically, our primary purpose is to conduct a good description of the role of N-WDP’s parameters on the secrecy performance of RIS-assisted networks. Furthermore, some useful insights for reaching secure communications in RIS-aided systems are provided, which are naturally connected to the physical parameters captured by the generalized channel model.

Notation: In what follows, uppercase and lowercase bold letters denote matrices and vectors, respectively; $f_{(·)}(·)$, probability density function (PDF); $F_{(·)}(·)$, the cumulative density function (CDF); $\mathcal{U}[a,b]$, a uniform distribution on $[a,b]$; ${\left(·\right)}^{\mathrm{T}}$, the transpose; $∥·∥$, the Euclidean norm of a complex vector; $\Gamma (·)$, the gamma function ([10], Equation (6.1.1)); ${\rm Y}(·,·)$, the lower incomplete gamma function ([10], Equation (6.5.2)); ${}_{2}F_1\left(·,·;·;·\right)$, the hypergeometric function ([10], Equation (15.1.1)); $\mathbb{C}$, the set of complex numbers; $\mathbb{E}[·]$, expectation; $\mathcal{B}\left(·,·\right)$, the Beta function ([10], Equation (6.2.2)); $\mathrm{diag}\left(\mathbf{x}\right)$, a diagonal matrix whose main diagonal is given by $\mathbf{x}$; $\mathcal{C}\mathcal{N}(·,·)$, the circularly symmetric Gaussian distribution; ${\mathbf{I}}_{\mathrm{N}}$, the identity matrix of size $N\times N$; ${\left(·\right)}^{\mathrm{H}}$, the Hermitian transpose; $\mathrm{mod}\left(·\right)$, the modulus operation; $⌊·⌋$, the floor function, and $sinc\left(w\right)=sin\left(\pi w\right)/\left(\pi w\right)$, the sinc function.

2. System and Channel Models

Assume a RIS-aided wiretap model composed of a transmitter, Alice (A) provided with M antennas, one legitimate node called Bob (B), one eavesdropper denoted by Eve (E), and a RIS, which helps the secure communication between A and B nodes. Specifically, a MISO system is assumed, where A sends information through its multiple antennas to a legitimate receiver B and an eavesdropper E, both of which have a single antenna. In this sense, the RIS helps to redirect the incident signal toward the legitimate receiver B, complicating the decoding of the message by eavesdropper E, as shown in Figure 1. In short, B and E are equipped with a single antenna, while the RIS has L nearly reconfigurable units. So, the received signal at E and B can be expressed as

$$y_i=\sqrt{P}\left({\mathbf{h}}_{2,i}^{\mathrm{T}}\mathbf{\Phi }\mathbf{G}+{\mathbf{h}}_{\mathrm{d},i}^{\mathrm{T}}\right)\mathbf{w}x+{\tilde{n}}_i,$$

(1)

in which $i\in \left\{\mathrm{B},\mathrm{E}\right\}$ is either the eavesdropper or the legitimate channel, x is the transmitted information symbol, P is the transmit power at A, $\tilde{n}\sim \mathcal{C}\mathcal{N}(0,{\sigma }_i^2)$ denotes the additive white Gaussian noise (AWGN) with ${\sigma }_i^2$ power, ${\mathbf{h}}_{\mathrm{d},i}\in {\mathbb{C}}^{M\times 1}$ is the channel between A and B or A and E, $\mathbf{w}$ $\in {\mathbb{C}}^{M\times 1}$ denotes the precoding vector at A, $\mathbf{G}=\left[{\mathbf{g}}_{\mathbf{1}},\dots ,{\mathbf{g}}_{\mathbf{M}}\right]\in {\mathbb{C}}^{L\times M}$ and ${\mathbf{h}}_{2,i}={\left[h_{2,i,1},\dots ,h_{2,i,L}\right]}^{\mathrm{T}}\in {\mathbb{C}}^{L\times 1}$ are the paths between A and RIS, RIS and B, or RIS and E, respectively. Furthermore, $\mathbf{\Phi }=\mathrm{diag}({\delta }_1{e}^{j{\phi }_1},\dots ,{\delta }_L{e}^{j{\phi }_L})$ is the phase-shift matrix generated by the RIS, where ${\delta }_l$ for $l=\left\{1,\dots ,L\right\}$ denotes the amplitude of the lth RIS element. Hereafter, it is considered that ${\delta }_l=1, \forall l$ in all subsequent derivations. The RIS adjusts the phase shifts for each unit to compensate for all phases created by the direct and indirect channels at the legitimate receiver, i.e., ${\phi }_l=\angle \left({\mathbf{h}}_{\mathrm{d},\mathrm{B}}^{\mathrm{H}}\mathbf{w}\right)-\angle \left(h_{2,\mathrm{B},l}^{\mathrm{H}}\right)-\angle \left({\mathbf{g}}_l\mathbf{w}\right)$ ([11], Equation (19)) where $h_{2,\mathrm{B},l}^{\mathrm{H}}$ is the lth element of ${\mathbf{h}}_{2,\mathrm{B}}^{\mathrm{H}}$ and ${\mathbf{g}}_l$ is the lth row vector from $\mathbf{G}$. In this configuration, both ${\phi }_l$ and the transmit precoding $\mathbf{w}$ are optimized together [11] to maximize the acquired signal-to-noise ratio (SNR) at $\mathrm{B}$. Nevertheless, the RIS forces a residual random phase error to prevail in practice. Here, such an error is denoted by ${\varphi }_l$, so the final phase shifts of the lth RIS unit change from the optima to ${\Theta }_l={\phi }_l+{\varphi }_l$ [11]. Therefore, the equivalent channel observed by the receivers can be formulated as

$$h_i=\left({\mathbf{h}}_{2,i}^{\mathrm{T}}\mathbf{\Psi }\mathbf{G}+{\mathbf{h}}_{\mathrm{d},i}^{\mathrm{T}}\right){\mathbf{w}}^{+},$$

(2)

where $\mathbf{\Psi }=\mathrm{diag}(e^{j{\Theta }_1},\dots ,e^{j{\Theta }_L})$ indicates the phase noise, and ${\mathbf{w}}^{+}=\frac{{\left({\mathbf{h}}_{2,\mathrm{B}}^{\mathrm{T}}\mathbf{\Psi }\mathbf{G}+{\mathbf{h}}_{\mathrm{d},\mathrm{B}}^{\mathrm{T}}\right)}^{\mathrm{H}}}{∥{\mathbf{h}}_{2,\mathrm{B}}^{\mathrm{T}}\mathbf{\Psi }\mathbf{G}+{\mathbf{h}}_{\mathrm{d},\mathrm{B}}^{\mathrm{T}}∥}$$\in {\mathbb{C}}^{M\times 1}$ is the maximal ratio transmission (MRT) precoding. Here, we decided to use the joint active and passive MRT precoding strategy from [11] because it is a low-complexity algorithm obtained on alternating optimization. In particular, the transmit precoding at A and the RIS’s phase shifts were optimized iteratively until meeting a pre-established criterion. It is worth pointing out that the MRT beamforming occurs when $\mathbf{w}$ is employed as a starting point in the distributed algorithm, which is updated in each iteration together with the RIS’s phase shifts. Concerning the channel model, we supposed that the fading coefficients of the underlying system are constructed as a superposition of N-dominant specular components plus scattering waves (i.e., the N-WDP model); so, it follows that [12]

$$\begin{array}{c}\hfill h_{\mathrm{d},i}^p=\sqrt{{\beta }_{\mathrm{d},i}}\left(\sum _{n=1}^{N_{\mathrm{d},i}}{V}_{\mathrm{d},i}^{(n,p)}{e}^{j{\theta }_{\mathrm{d},i}^{(n,p)}}+Z_{\mathrm{d},i}^{\left(p\right)}\right),h_{2,i,l}=\sqrt{{\beta }_{2,i}}\left(\sum _{n=1}^{N_{\mathrm{RIS},i}}{V}_{2,i}^{(n,l)}{e}^{j{\theta }_{2,i}^{(n,l)}}+Z_2^{\left(l\right)}\right)\end{array}$$

(3)

$$\begin{array}{cc}\hfill g_{l,p}=& \sqrt{{\beta }_1}\left(\sum _{n=1}^{N_{\mathrm{A},\mathrm{RIS}}}{V}_1^{(n,p,l)}{e}^{j{\theta }_1^{(n,p,l)}}+Z_1^{(p,l)}\right),\hfill \end{array}$$

(4)

for $p=\left\{1,\dots ,M\right\}$, and $l=\left\{1,\dots ,L\right\}$. Here, $V_{(·)}^{(n,·)}$ symbolize the amplitude of an nth specular component, ${\theta }_{(·)}^{(n,·)}\sim \mathcal{U}[0,2\pi ]$ and $N_{\left(f\right),\left(u\right)}$ indicate the total number of dominant components of the channel between nodes f and u, and $Z_{(·)}^{(·)}$ follow Rayleigh with ${\mathbb{E}\left\{\right|Z|}^2\}=2{\sigma }^2={\Omega }_0$, indicating the diffuse received waves. The terms ${\beta }_1$, ${\beta }_{2,i}$, and ${\beta }_{\mathrm{d},i}$ encompass the path loss for A-RIS, RIS-i, and A-i links for $i\in \left\{\mathrm{B},\mathrm{E}\right\}$, respectively. Notice that the N-WDP model includes important stochastic fading models such as TWDP, Rician, and Rayleigh as special cases for $N_{(·)}=2,1,1$, respectively. Now, to evaluate spatial correlation for the RIS channels, the geometry network proposed in [13] is employed. Hence, we assumed that the RIS is a surface consisting of L elements, where $L_V$ and $L_H$ are the total units per row and per column, respectively. In this regard, the area of an individual RIS element is expressed by $A=d_H{d}_V$, with $d_H$ and $d_V$ denoting the vertical height and the horizontal width, respectively. Based on this, and by assuming an isotropic diffuse environment, the indirect RIS fading channels subject to correlation and the direct link can defined as ${\mathbf{h}}_{\mathrm{d},i}={\left[h_{\mathrm{d},i}^1,\dots ,h_{\mathrm{d},i}^M\right]}^{\mathrm{T}},{\mathbf{h}}_{2,i}=\sqrt{A\mathbf{R}}{\left[h_{2,i,1},\dots ,h_{2,i,L}\right]}^{\mathrm{T}},{\mathbf{g}}_p=\sqrt{A\mathbf{R}}{\left[g_{1,p},\dots ,g_{L,p}\right]}^{\mathrm{T}}$, where $p=\left\{1,\dots ,M\right\}$, $\mathbf{R}\in {\mathbb{C}}^{L\times L}$ is the spatial correlation matrix for the RIS. The $(a,b)$th-entry of $\mathbf{R}$ is given by ${\left[\mathbf{R}\right]}_{a,b}=sinc\left(2∥{\mathbf{u}}_a-{\mathbf{u}}_b∥/\lambda \right)a,b=1,\dots ,L$ [13], where ${\mathbf{u}}_{\zeta }={\left[0,\mathrm{mod}\left(\zeta -1,L_H\right)d_H,⌊\left(\zeta -1\right)/L_H⌋d_V\right]}^T$, $\zeta \in \left\{a,b\right\}$, and $\lambda$ is the wavelength of the wave. With the previous expressions, the received SNR at $\mathrm{B}$ or $\mathrm{E}$ is formulated by

$$\begin{array}{cc}\hfill {\gamma }_i=& {\displaystyle \frac{P|h_i{|}^2}{{\sigma }_i^2}}={\overline{\gamma }}_i{\left|h_i\right|}^2.\hfill \end{array}$$

(5)

Now, ${\overline{\gamma }}_i=P/{\sigma }_i^2$ is defined as the average transmit SNR for $\mathrm{B}$ or $\mathrm{E}$. As a first stage, the purpose is to approximate the magnitude of $h_i$ using some statistical distribution. For this purpose, we employed the EM learning algorithm, as follows:

3. RIS Channel Characterization

Here, using a simple mixture of Nakagami-m random variables (RVs) combined with the EM strategy, the end-to-end RIS channel was characterized in a simple manner.

Let ${\mathbf{h}}_i={\left\{h_i\right\}}_1^t$ be a training set vector of t samples of $h_i$ in (2); it is approximated that $h_i$ is observed by B and E using a mixture of Nakagami-m distributions, as follows [14]:

$$\begin{array}{cc}\hfill f_{h_i}\left(r_i\right)\approx & \sum _{z=1}^{\mathcal{C}}{\omega }_{z,i}{\mathcal{N}}_{z,i}\left(r_i;m_{z,i},{\Omega }_{z,i}\right),\hfill \end{array}$$

(6)

where $\mathcal{C}$ is the mixture size (i.e., the number of Nakagami-m components), ${\mathcal{N}}_{z,i}\left(r_i;m_{z,i},{\Omega }_{z,i}\right)=\frac{m_{z,i}^{m_{z,i}}{r}_i^{2m_{z,i}}{e}^{-\frac{m_{z,i}{r}_i^2}{{\Omega }_{z,i}}}}{2^{-1}\Gamma \left(m_{z,i}\right){\Omega }_{z,i}^{m_{z,i}}{r}_i}$, ${\omega }_{z,i}\in \left\{1,\dots ,\mathcal{C}\right\}$ with ${\sum }_{z=1}^{\mathcal{C}}{\omega }_{z,i}=1$ and $0\le {\omega }_{z,i}\le 1$ are the mixture weights, and ${\Omega }_{z,i}$ and $m_{z,i}$ are the mean powers and the fading elements of the weighted PDFs, respectively. Here, we refer to the unsupervised EM method to fit the mixture parameters. Specifically, in the expectation (E)-step of the EM technique, the posterior probabilities (i.e., membership values) of the zth-weighted PDF of both B and E can be calculated as [14]

$${\tau }_{zj,i}^{\left(k\right)}={\displaystyle \frac{{\omega }_{z,i}{\mathcal{N}}_{z,i}\left(h_{i,j};m_{z,i},{\Omega }_{z,i}\right)}{{\sum }_{l=1}^{\mathcal{C}}{\omega }_{l,i}{\mathcal{N}}_{l,i}\left(h_{i,j};m_{z,i},{\Omega }_{z,i}\right)}},z=1,\dots ,\mathcal{C},j=1,\dots ,t,$$

(7)

where k represents the present iteration, t is the size of the sample set in (2), $h_{i,j},\forall j=1\dots t$ are the unlabeled samples at the receiver node $i\in \left\{\mathrm{B},\mathrm{E}\right\}$, and z is the mixture component. Next, in the M-step of the EM algorithm, the updated parameters are fitted by maximizing the log-likelihood formulation of each RV-weighted mixture via the posterior probabilities. Hence, the updated parameters of the receive sides can be calculated as [14]

$$\begin{array}{cc}\hfill {\Omega }_{z,i}^{(k+1)}=& {\displaystyle \frac{{\sum }_{j=1}^t{\tau }_{zj,i}^{\left(k\right)}{h}_{i,j}^2}{{\sum }_{j=1}^t{\tau }_{zj,i}^{\left(k\right)}}}{m}_{z,i}^{(k+1)}={\displaystyle \frac{1+\sqrt{1+\frac{4{\Delta }_{z,i}^k}{3}}}{4{\Delta }_{z,i}^k}}\hfill \\ \hfill {\omega }_{z,i}^{(k+1)}=& {\displaystyle \frac{{\sum }_{j=1}^t{\tau }_{zj,i}^{\left(k\right)}}{t}},{\Delta }_{z,i}^k={\displaystyle \frac{{\sum }_{j=1}^t{\tau }_{zj,i}^{\left(k\right)}\left[log\left({\Omega }_{z,i}\right)-log\left(h_{i,j}^2\right)\right]}{{\sum }_{j=1}^t{\tau }_{zj,i}^{\left(k\right)}}}\hfill \end{array}$$

(8)

Algorithm 1 displays the EM Nakagami-m mixture model, where the initial mixture weights are randomly selected from $\mathcal{U}[0,1]$, and the start values for the scaling parameters of Nakagami-m PDFs are calculated using the maximum likelihood estimation (MLE). Also, comparable toleration practice is employed as a stopping criterion. It is worth pointing out that the EM can efficiently model any target system’s wireless channel considered in (2). In fact, EM can also be utilized even with experimental measurement channel data.   

Algorithm 1: Unsupervised EM machine learning algorithm for fitting ${\omega }_i$, ${\Omega }_i$, and $m_i$ of Nakagami-m RVs

4. RIS Secrecy Performance

4.1. Distribution of ${\gamma }_{\mathrm{E}}$ and ${\gamma }_{\mathrm{B}}$

The PDFs and CDFs of the received SNR in $\mathrm{E}$ and $\mathrm{B}$, respectively, are acquired by performing a transformation of variables from (5). Thus, this yields

$$f_{\mathrm{E}}\left({\gamma }_{\mathrm{E}}\right)=\sum _{z=1}^{\mathcal{C}}\frac{{\gamma }_{\mathrm{E}}^{{\kappa }_{z,\mathrm{E}}-1}}{{\left({\overline{\gamma }}_{\mathrm{E}}{\theta }_{z,\mathrm{E}}\right)}^{{\kappa }_{z,\mathrm{E}}}\Gamma \left({\kappa }_{z,\mathrm{E}}\right)}{e}^{\left(-{\displaystyle \frac{{\gamma }_{\mathrm{E}}}{{\overline{\gamma }}_{\mathrm{E}}{\theta }_{z,\mathrm{E}}}}\right)},F_{\mathrm{B}}\left({\gamma }_{\mathrm{B}}\right)=\sum _{z=1}^{\mathcal{C}}{\displaystyle \frac{{\rm Y}\left({\kappa }_{z,\mathrm{B}},\frac{{\gamma }_{\mathrm{B}}}{{\overline{\gamma }}_{\mathrm{B}}{\theta }_{z,\mathrm{B}}}\right)}{\Gamma \left({\kappa }_{z,\mathrm{B}}\right)}}$$

(9)

where ${\kappa }_{z,i}=m_{z,i}$ and ${\theta }_{z,i}={\Omega }_{z,i}/m_{z,i}$.

4.2. Secrecy Outage Probability (SOP)

This metric is useful for passive eavesdropping scenarios where Eve channel’s channel state information (CSI) is not known at Alice. Thus, Alice encodes the information at an unchanging secrecy rate $R_{\mathrm{S}}$. Based on [15], the secrecy capacity, i.e., $C_{\mathrm{S}}$, is calculated as $C_{\mathrm{S}}=\max \left\{C_{\mathrm{B}}-C_{\mathrm{E}},0\right\},$ with $C_{\mathrm{B}}={log}_2(1+{\gamma }_{\mathrm{B}})$ and $C_{\mathrm{E}}={log}_2(1+{\gamma }_{\mathrm{E}})$ being the channel capacities at $\mathrm{B}$ and $\mathrm{E}$, respectively. Here, secrecy is attained only when $R_{\mathrm{S}}\le C_{\mathrm{S}}$, and it is compromised otherwise. Mathematically speaking, a lower bound of the SOP can be determined as [15] ${\mathrm{SOP}}_{\mathrm{L}}\left(R_{\mathrm{S}}\right)={\int }_0^{\infty }{F}_{{\gamma }_{\mathrm{B}}}\left(2^{R_{\mathrm{S}}}{\gamma }_{\mathrm{E}}\right)f_{{\gamma }_{\mathrm{E}}}\left({\gamma }_{\mathrm{E}}\right)d{\gamma }_{\mathrm{E}}$. Hence, an approximation of the ${\mathrm{SOP}}_{\mathrm{L}}$ can obtained as stated below.

Proposition 1.

The ${\mathit{SOP}}_{\mathrm{L}}$ for RIS-assisted MISO networks under generalized fading is approximated as

$$\begin{array}{cc}\hfill & {\mathrm{SOP}}_{\mathrm{L}}\left(R_{\mathrm{S}}\right)=\sum _{s=1}^{\mathcal{C}}\sum _{z=1}^{\mathcal{C}}{\omega }_{s,\mathrm{B}}{\omega }_{z,\mathrm{E}}{\left(\frac{{\overline{\gamma }}_{\mathrm{E}}{\theta }_{z,\mathrm{E}}}{{\overline{\gamma }}_{\mathrm{B}}{\theta }_{s,\mathrm{B}}}\right)}^{{\kappa }_{s,\mathrm{B}}}\frac{2^{R_{\mathrm{S}}{\kappa }_{s,\mathrm{B}}}}{{\kappa }_{s,\mathrm{B}}\mathcal{B}\left({\kappa }_{s,\mathrm{B}},{\kappa }_{z,\mathrm{E}}\right)}{}_{2}F_1\left({\kappa }_{s,\mathrm{B}}+{\kappa }_{z,\mathrm{E}},{\kappa }_{s,\mathrm{B}};1+{\kappa }_{s,\mathrm{B}};-\frac{2^{R_{\mathrm{S}}}{\overline{\gamma }}_{\mathrm{E}}{\theta }_{z,\mathrm{E}}}{{\overline{\gamma }}_{\mathrm{B}}{\theta }_{s,\mathrm{B}}}\right).\hfill \end{array}$$

(10)

Proof. 

${\mathrm{SOP}}_{\mathrm{L}}$ can be easily derived from ([16], Equation (7)), with the corresponding substitutions of (9), and after some mathematical manipulations. □

4.3. Average Secrecy Rate (ASR)

This metric is relevant for the active eavesdropping case, where Alice knows the CSI of both Bob and Eve channels. Alice can guarantee secrecy by adjusting her transmission rate subject to $R_{\mathrm{S}}$. Based on [17], the ASR can be computed as $\mathrm{ASR}={\int }_0^{\infty }\left(1-{\mathrm{SOP}}_{\mathrm{L}}\left(x\right)\right)dx.$

Proposition 2.

The ASR expression of the RIS underlying network is approximated by

$$\begin{array}{c}\hfill \mathit{ASR}\approx \sum _{c=1}^{\eta }{\xi }_c{e}^{-x_c}{u}_1\left(x_c\right),\end{array}$$

(11)

where $u_1\left(x_c\right)=e^{x_c}(1-{\mathit{SOP}}_{\mathrm{L}}\left(x_c\right))$ and $x_c$ and ${\xi }_c$ are the cth zero (root) and weight of the ηth-order Laguerre polynomial ([10], Equation (22.2.13)).

Proof. 

Based on Gauss–Laguerre quadrature technique ([10], Equation (25.4.45)), the exact ASR can be approximated by a weighted sum of samples. □

4.4. Average Secrecy Loss (ASL)

This novel secrecy metric relates to the information leaked from A to E. Using ([17], Equation (9)), the ASL is expressed as in the following proposition.

Proposition 3.

The ASL formulation of the underlying network is expressed as

$$\begin{array}{c}\hfill \mathit{ASL}\approx {\displaystyle \frac{{\sum }_{j=1}^{\upsilon }{\rho }_j{e}^{-x_j}{u}_2\left(x_j\right)}{{\mathit{ASR}}^2}}-1,\end{array}$$

(12)

where $u_2\left(x_j\right)=2x_j{e}^{x_j}(1-{\mathit{SOP}}_{\mathrm{L}}\left(x_j\right))$, $x_j$, and ${\rho }_j$ are the jth zero (root) and weight of the υth-order Laguerre polynomial ([10], Equation (22.2.13)).

Proof. 

Again, the Gauss–Laguerre quadrature approach is used to approximate the integral ([17], Equation (10)), which involves the computation of the exact ASL. □

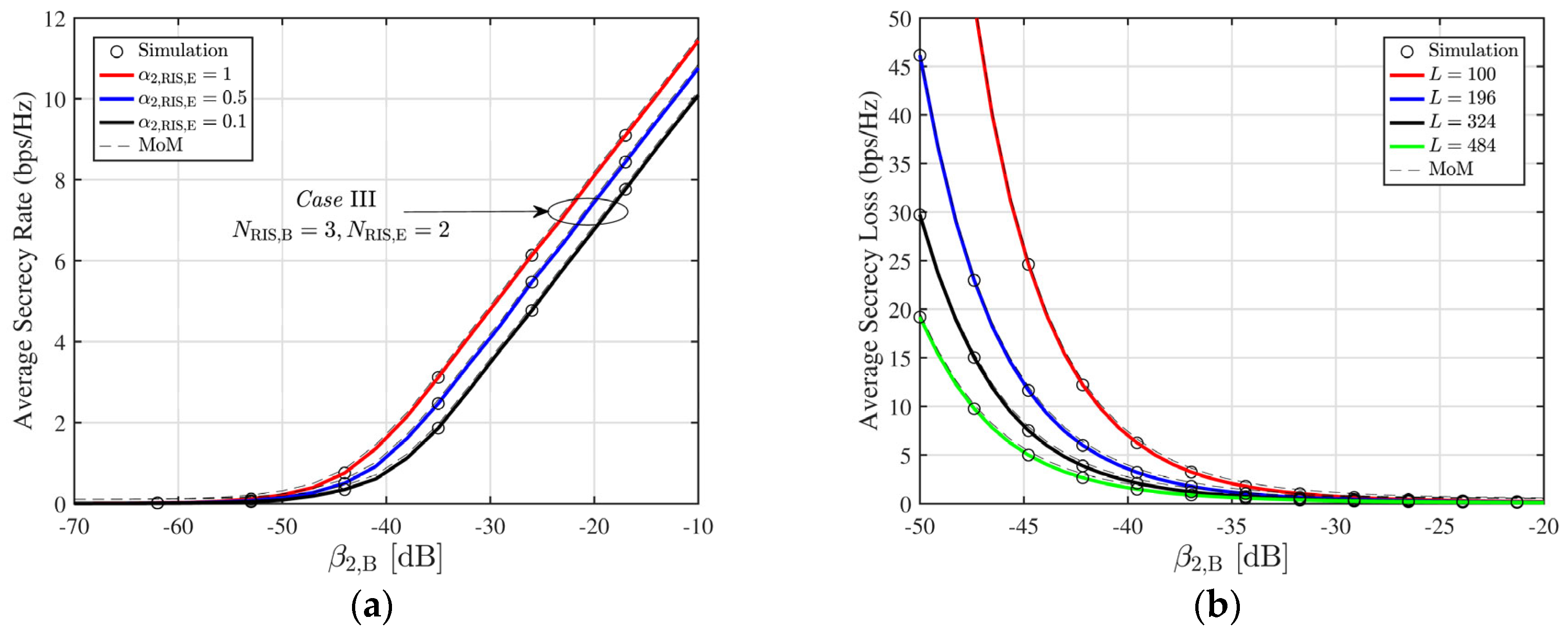
5. Numerical Results and Discussions

Here, we investigated how correlated channels over generalized fading impact the system’s secrecy performance, assuming discrete phase shifts, as well as the goodness-of-fit of the approximations for the RIS channels. Monte Carlo (MC) simulations for EM-based approximations are included in all instances with markers. For the sake of comparison, the well-known moment matching method (MoM) (For informative purposes and to compare the MoM with the proposed method fairly) models the end-to-end channel in (2) through a Nakagami-m distribution. Here, the fitting parameters were obtained numerically by calculating the moments and equating them to the parameters of the Nakagami-m distribution, as indicated by the MoM procedure in ([18], Sec. III).) proposed in [18] for modeling generalized RIS channels (i.e., (2)) is included as a baseline in the secrecy analysis. Also, to estimate the parameters of the Nakagami-m mixture model with the EM method, ${10}^5$ realizations are generated for the unlabeled training set in (2), which is required in Algorithm 1 for both Bob and Eve. Specifically, these generated channel coefficients are the observations, constituting the input in Algorithm 1. With the output of Algorithm 1 (e.g., ${\omega }_{z,i}$, ${\Omega }_{z,i}$, and $m_{z,i}$), these fitting parameters are used in (9) to be later substituted into (10)–(12); in this way, the performance of the underlying system model is evaluated. The discrete phase shift ${\varphi }_l$ is built from $\mathcal{U}[-2^{-q}\pi ,2^{-q}\pi ]$, where $q\ge 1$ is the amount of quantization bits utilized to encode the phase shifts errors, i.e., the discrete set of $2^q$ phases that can be configured on the RIS (a larger q refers to smaller phase errors on RIS’s configuration).

In all figures, the following considerations are assumed: (i) a RIS-aided network system given in [13] with a frequency of 3 GHz (i.e., $\lambda =0.1$ m), $BW=1$ MHz of bandwidth, a transmit power of $P=23$ dBm, and an AWGN with a power spectral density of $N_0=-174$ dBm/Hz. Hence, ${\sigma }_i^2=N_{0}BW=-114$ dBm, which makes $P/{\sigma }_i^2={\overline{\gamma }}_i=137$ dB, (ii) $R_{\mathrm{S}}=1$ bps/Hz for all SOP curves, and (iii) $\mathcal{C}=2$ as the number of components of the Nakagami-m mixture.

Moreover, only Figure 2b includes both direct and indirect links. For mathematical compactness, the power ratio parameter is represented as being analogous to the Rician K factor, i.e., $K_{N_{(·)}}\stackrel{\Delta }{=}{\displaystyle \frac{{\Omega }_{N_{(·)}}}{{\Omega }_0}}$, with ${\Omega }_{N_{(·)}}={\sum }_{n=0}^{N_{(·)}}{\left(V_{(·)}^{(n,·)}\right)}^2$ being the total average power of the dominant components. Also, $K_{\mathrm{dB}}^{(·)}=10{log}_{10}\left(K_{(·)}=K_{N_{(·)}}\right)$ is defined. Likewise, the amplitudes of corresponding rays are depicted in terms of the amplitude of the first dominant component, i.e., $V_{(·)}^{(n,·)}={\alpha }_{n,(·)}{V}_{(·)}^{(1,·)}$ for $n=\left\{2,\dots ,N_{(·)}\right\}$, with $0<{\alpha }_{n,(·)}<1$. Figure 2a shows the SOP vs. ${\beta }_{2,\mathrm{B}}$ for different channel setups. Here, the following cases are assumed. Case $\mathrm{I}$: The legitimate paths are subject to Rician fading, i.e., $N_{\mathrm{A},\mathrm{RIS}}=N_{\mathrm{RIS},\mathrm{B}}=1$ with $V_1^{(1,·)}=V_{2,\mathrm{B}}^{(1,·)}=1$ for $K_{\mathrm{dB}}^{\mathrm{A},\mathrm{RIS}}=K_{\mathrm{dB}}^{\mathrm{RIS},\mathrm{B}}=12$ dB, and the eavesdropper link, i.e., RIS-to-E, follows Rayleigh fading (i.e., $N_{\mathrm{RIS},\mathrm{E}}=0$). Case $\mathrm{II}$: All channels follow Rayleigh fading (i.e., the classical assumption). For the aforementioned cases, the remaining system parameters are $M=5$, $L=144$, $q=5$, ${\beta }_1=-20$ dB, ${\beta }_{2,\mathrm{E}}=-30$ dB, and $d_H=d_V\in \left\{\lambda /2,\lambda /5\right\}$. Here, the impact of dealing with both Rician fading and RIS-correlated channels is explored. From all traces, we observed that a more favorable channel propagation for legitimate links (i.e., Rician fading) contributes to improving the SOP performance with respect to Rayleigh propagation’s counterpart. Moreover, revealing SOP behavior is observed depending on the strength of the correlation on RIS channels. For instance, decreasing the size of RIS units (i.e., hard-correlated RIS channels) leads to lower secrecy performance.

Figure 2b illustrates the SOP vs. ${\beta }_{2,\mathrm{B}}$ when both Bob and Eve have a direct path. Here, all the indirect paths, i.e., A-to-RIS, RIS-to-B, and RIS-to-E, follow Rayleigh fading. However, the direct links, i.e., A-to-B and A-to-E, are subject to TWDP fading. Thus, $N_{\mathrm{d},\mathrm{E}}=N_{\mathrm{d},\mathrm{B}}=2$ with $V_{\mathrm{d},\mathrm{E}}^{(1,·)}=V_{\mathrm{d},\mathrm{B}}^{(1,·)}=1$, ${\alpha }_{2,\mathrm{d},\mathrm{B}}={\alpha }_{2,\mathrm{d},\mathrm{E}}=0.7$ for $K_{\mathrm{dB}}^{\mathrm{d},\mathrm{B}}=K_{\mathrm{dB}}^{\mathrm{d},\mathrm{E}}=18$ dB. The remaining parameters are set to $M=8$, $L=196$, $A{\beta }_1=-30$ dB, $A{\beta }_{2,\mathrm{E}}=-50$ dB, and $d_H=d_V=\lambda /3$. From this figure, we observed that the combination of mild path loss (i.e., ${\beta }_{\mathrm{d},i}=-40$ dB) and good propagation conditions (i.e., TWDP fading) on Bob’s direct link is favorable to achieve better secrecy performance. Also, for this scenario, notice that the RIS does not contribute significantly to the system’s performance due to the presence of a strong LoS for Bob and Eve’s links. However, the SOP’s behavior changes slightly from ${\beta }_{2,\mathrm{B}}\approx -20$ dB since the RIS-to-B link presents better channel conditions than the direct A-to-B link. Therefore, the RIS begins to operate in this region, and a difference in the phase error’s configuration is observed. Now, when direct paths are heavily attenuated (i.e., ${\beta }_{\mathrm{d},i}=-90$ dB), the use of the RIS makes sense in this case since different performances of the SOP are obtained by varying q.

Figure 3a presents the ASR vs. ${\beta }_{2,\mathrm{B}}$. In this figure, base values (i.e., baseline fading channel models) are considered to measure the system’s performance by setting different propagation conditions. Also, the following scenarios are considered: Case $\mathrm{III}$: A-to-RIS link (Rician), $N_{\mathrm{A},\mathrm{RIS}}=1$ with $V_1^{(1,·)}=1$ for $K_{\mathrm{dB}}^{\mathrm{A},\mathrm{RIS}}=25$ dB. RIS-to-B link (three rays), $N_{\mathrm{RIS},\mathrm{B}}=3$ with $V_{2,\mathrm{B}}^{(1,·)}=1$, ${\alpha }_{n,\mathrm{RIS},\mathrm{B}}=0.1$ for $n=\left\{2,3\right\}$, and $K_{\mathrm{dB}}^{\mathrm{RIS},\mathrm{B}}=25$ dB. RIS-to-E link (TWDP), $N_{\mathrm{RIS},\mathrm{E}}=2$ with $V_{2,\mathrm{E}}^{(1,·)}=1$, ${\alpha }_{2,\mathrm{RIS},\mathrm{E}}\in \left\{1,0.5,0.1\right\}$ for $K_{\mathrm{dB}}^{\mathrm{RIS},\mathrm{E}}=25$ dB. Also, $M=6$, $L=196$, $q=4$, $A{\beta }_1=A{\beta }_{2,\mathrm{E}}=-50$ dB, and $d_H=d_V=\lambda /4$. Herein, the impact of Eve’s fading TWDP parameters on the ASR performance is explored. From all traces, notice that there is a mixture of more dominant paths in B than E and that lower amplitude values associated with Eve’s rays (i.e., ${\alpha }_{2,\mathrm{RIS},\mathrm{E}}$) lead to poor ASR performance. This result verifies that the amplitudes of the specular waves play relevant roles in secure communication criteria of over-generalized channel conditions.

Figure 3b depicts the ASL vs. ${\beta }_{2,\mathrm{B}}$ by altering the elements at the RIS. For this scenario, we considered that all indirect paths follow Rician fading, i.e., $N_{\mathrm{A},\mathrm{RIS}}=N_{\mathrm{RIS},\mathrm{B}}=N_{\mathrm{RIS},\mathrm{E}}=1$ with $V_1^{(1,·)}=V_{2,\mathrm{B}}^{(1,·)}=V_{2,\mathrm{E}}^{(1,·)}=1$ for $K_{\mathrm{dB}}^{\mathrm{A},\mathrm{RIS}}=K_{\mathrm{dB}}^{\mathrm{RIS},\mathrm{B}}=K_{\mathrm{dB}}^{\mathrm{RIS},\mathrm{E}}=20$ dB. Furthermore, $M=4$, $q=6$, $A{\beta }_1=A{\beta }_{2,\mathrm{E}}=-45$ dB, and $d_H=d_V=\lambda /3$. From all instances, it was observed that information leakage was drastically reduced as the number of elements on the RIS increased. Here, the ASL shows how much ${\beta }_{2,\mathrm{B}}$ the system needs to drive the information leak to zero. For instance, in the proposed setup, from ${\beta }_{2,\mathrm{B}}\approx -35$ dB, communication between legitimate links is secure. In addition, notice that in all the analyzed curves, the proposed approximation beats the MoM in precision, mainly in the secrecy outage-based metric. Finally, it is worth mentioning that an energy consumption parameter that integrates energy collection from environmental sources with secure communication mechanisms at the physical layer is not considered. However, this topic is out of this paper’s scope and will be explored in the future.

6. Conclusions

The secrecy performance of the RIS-assisted wiretap MISO system by assuming generalized fading channels and discrete phase shifts was explored. Specifically, secrecy metrics such as the SOP, ASR, and ASL were obtained in closed-form expression to evaluate the secure performance by approximating the end-to-end RIS channel through an unsupervised EM learning algorithm. Some insights reveal how different propagation conditions and RIS practical implementation (e.g., discrete phase-shift noise, spatial correlation, beamforming, presence of direct link) impact secrecy performance. For instance, when the direct link is present in the communication between Alice and Bob, using a RIS is practically unnecessary despite correctly configuring the phase error. On the contrary, when only the non-line-of-sight link between Alice and Bob is available, RIS technology is essential so that the information does not leak to the eavesdropper.