Sensor Placement and State Estimation in Water Distribution Systems Using Edge Gaussian Processes ^†

Abstract

The operation of water distribution systems is based on reliable knowledge about the steady state of the system. This involves sensors to measure flow, facilitating a comprehensive overview of the system’s performance. Given the costs associated with sensor installation and operation, it is important to be strategic with sensor allocation. Recently developed Gaussian Processes with topological kernels can efficiently model mass and energy conservative flows and provide uncertainty bounds. Our work proposes a novel method of state estimation and a greedy search algorithm for water flow meter placement based on the uncertainty bounds provided by a Gaussian Process.

1. Introduction

The main challenge of planning a monitoring scheme for a water distribution system (WDS) is striking a balance between maximizing the observability and the cost. Most attempts to tackle this challenge use computationally expensive optimization processes that can be prohibitive for large networks [1]. Approaches based on graph theory provide a remedy; however, they do not account for physical laws that govern the system [2].

Recent advancements in geometric deep learning enable the incorporation of network topology and physical laws into the model [3]. This includes novel Gaussian Processes with topological kernels that can efficiently model mass and energy conservative flows. By including connectivity information into the kernel, Gaussian Processes (GPs) can interpolate flows in a network based on mass-conservation principles. Consequently, the variance of the GP can serve as an indicator of uncertainty. Our work proposes a greedy search algorithm for water flow meters based on the uncertainty of the estimated flowrates.

2. Materials and Methods

2.1. Problem Statement

We define a directed graph $G=\left(V,E\right)$ that describes a water distribution system. The set of nodes $V$ corresponds to the junction, reservoirs, and tanks, while the set of edges $E$ represents the pipes. The direction of the edges is chosen arbitrarily. The matrix $B_1\in R^{\left|V\right|\times \left|E\right|}$ denotes the incidence between edges and nodes of the graph [4]. We additionally define a set of loops $C$ in the network and assign an arbitrary orientation. Similarly, $B_2\in R^{\left|E\right|\times \left|C\right|}$ is an incidence between the cells and incidental edges.

We assume noisy demands on the nodes $q\in R^{\left|N_c\right|}$ and flowrate sensors, where $N_c$ is the number of consumption nodes, and a set of $k$ sensor edges, i.e., water flow meters. The desired output is the vector of flowrates on the pipes $f\in R^{\left|E\right|-k}$ along with the uncertainty bounds. The negative sign of the vector value means that the true direction of the flow is the opposite to the one selected. We are additionally interested in finding the set $S$ of $k$ best sensor locations out of set $E$.

2.2. Flowrate Estimation with Gaussian Processes

Let X be a set of pipes. A flowrate vector can be modeled with a multi-dimensional Gaussian process $f\sim GP\left(\mu ,k\right)$, with mean vector $\mu =\mu \left(x\right)$ and covariance matrix $K=R^{\left|E\right|\times \left|E\right|}$. We assume that the prior mean $\mu$ is zero. The resulting function on the edges $f\left(x\right)$ is assumed to follow a multivariate Gaussian distribution where each dimension in it corresponds to a pipe.

For a given set of sensor locations and sensor measurements $\left(x_i,y_i\right)$, we define the model $y_i=f\left(x_i\right)+{ϵ}_i$, where $f\sim GP\left(0,k\right)$ and noise ${ϵ}_i\sim N\left(0,{\sigma }^2\right)$. The posterior of $f$, given the observations at $x_i$, is another GP. Its conditional mean and covariance at the rest of the pipes (.) are as follows:

$${\left.\mu \right|}_y\left(.\right)=K_{.x}{\left(K_{xx}+{\sigma }^{2}I\right)}^{-1}y$$

(1)

$${\left.K\left(.,.\prime \right)\right|}_y=k\left(.,.\prime \right)-K_{.x}{\left(K_{xx}+{\sigma }^{2}I\right)}^{-1}{K}_{x.\prime }$$

(2)

The result of the posterior is a multi-variate distribution of flowrates, conditioned by known flowrates at sensor locations. The predicted flowrates can be extracted as the mean of the Gaussian flowrates.

2.2.1. Mass-Conservative Covariance

The mass conservation principle states that all incoming water flows are equal to the outflow.

$$B_{1}f=q$$

(3)

Recent works introduce a kernel that describes the relationship between the values defined on the edges of the graph. In fact, if the covariance is selected as $L_{down}^H$= $e^{-B_1^T{B}_1}$, the sampled $f$ will be mass conservative [3].

To ensure energy conservation, the sampled flowrates are transformed using the Hazen–Williams relation into headlosses $h$. As the relation is non-linear, the distribution of $h$ is no longer Gaussian. Energy conservation can be assured by projecting $h$ with a linear operator $L_{up}^H$ = $e^{B_2{B}_2^T}$ [5].

$$h^{\prime }=L_{up}^{H}h$$

(4)

The resulting $h^{\prime }$ are energy conservative, meaning that the sum of energy losses within a closed loop with respect to their orientations are equal to 0.

2.2.2. Virtual Edges

To incorporate the demand on the nodes into the estimation, we propose to extend the graph $G$ with $\left|V\right|$ virtual nodes paired with each real node. As a result, $q$ on the corresponding nodes act as sensory input on pipes to GP.

2.3. Sensor Placement

The sensor placement strategy is based on the greedy selection of the GP dimension with the highest variance. The algorithm iteratively updates the set of sensors $S$ and evaluates ${\left.\mu \right|}_y$ and $K{|}_y$, applying Equations (1) and (2). The latter estimates the uncertainty of the prediction. This strategy is akin to the Bayesian optimization procedure [6].

2.4. Evaluation

Algorithm 1 is evaluated based on 3 benchmark networks: Zhi-Jiang [7], area C of L-Town [8], and Net-3 [9]. The initial set $S$ of sensors is selected as the flowrates on virtual edges (i.e., demands and reservoir outflows), k = 10. For Net-3, we additionally visualize the location of the sensors. The accuracy of the state estimation is evaluated with the R² of flowrates on unknown pipes against the ones obtained via EPANET [9].

Algorithm 1. Sensor Placement Strategy

Input: Covariance K, $k$, $x\subset E$, $S$ for j = 1 to k: Update K according (1) and (2) $\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}h\left(x\right)\leftarrow HazenWilliams\left(f\left(x\right)\right)$ $\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}h\prime \left(x\right)\leftarrow L_{up}^{H}h\left(x\right)$ $\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}f\left(x\right)\leftarrow HazenWilliam{s}^{-1}\left(h\left(x\right)\right)$ $\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{S}_x^{argmax}=Var\left(f\left(x\right)\right)$ $\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}S\leftarrow S\cup S^{\prime }$ end

3. Results

Figure 1a visualizes the dynamics of errors of the estimated flowrates against the number of flow meters installed in the network. The estimation accuracy increases with the number of sensors. For ZJ and L-Town, the largest gain is visible with the first suggestion as the accuracy reaches 0.99 in R². However, further suggestions are less informative. In the example of Net-3, the accuracy gradually increases with the number of flowrate sensors and reaches 0.97.

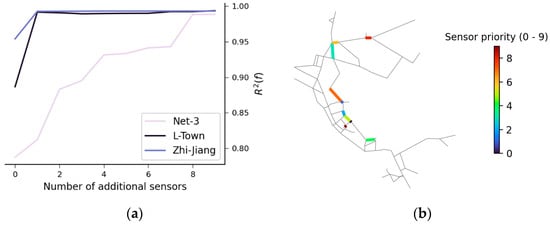
Figure 1. Results of a sensor placement algorithm. (a) Ten selected sensor locations on the example of Net-3. (b) Accuracy of the flowrate estimation.

4. Discussion

For ZJ and L-Town, the sensor placement algorithm prioritizes the allocation of sensors on the pipes that are located next to the reservoir. Assuming the demands are known with some noise factor, these pipes are the most influential for estimating water flow in the pipes. Figure 1b shows that the algorithm prioritizes the pipes that act as bottlenecks and influence the rest of the network.

The difference in the accuracy between the networks requires further investigation.

Currently, the algorithm shows the preliminary results on simple networks and requires further investigation. Further work can include pressure sensor placement and can combine multiple Gaussians to incorporate energy conservation more thoroughly.

5. Conclusions

This work introduces a novel method of estimation of flowrates and uncertainty bounds based on GP. We additionally propose a greedy water flow sensor placement algorithm that systematically prioritizes pipes in the water network with the highest uncertainty of estimated flowrates. This approach is similar to the exploration objective based on the acquisition function of Bayesian optimization. For simple networks, this allows for interpolating the flowrates with assumed demands and a single flowrate sensor with high accuracy. Finally, by omitting the need to run expensive hydraulic simulations, we provide a fast sensor-placement technique that is both geometrically and physically informed.