Abstract
The utilization of conventional fossil fuel-based energy for power generation is associated with various issues, such as greenhouse gas emissions, rising costs, and scarcity of resources. Renewable energy sources offer a solution to these problems. Although solar photovoltaic technologies have been leading the way in this area, the output of solar cells is constrained by optical losses. Surface texturing reduces reflectance, increasing the absorbance of solar cells. Therefore, it is necessary to obtain proper values of texturing parameters before fabricating the solar cell. Software simulation tools can help to do this. In the present work, the PC1D 5.0 tool is used to obtain an optimum texture thickness and angle for a solar cell of a 100 cm2 cross-sectional area. For the texture angle of 65°, the optimum texture was found to be 4 µm.
1. Introduction
The advancement of any nation hinges on several critical factors, including social growth, industrial progress, economic growth, and electrical energy capacity [1]. The global requirement for energy is perpetually increasing [2]. Hence, conventional energy sources do not match up to rising energy demand [3]. Moreover, these conventional energy generation techniques are major sources of pollution. Environmental protection agencies worldwide have devised and enforced various policies to mitigate or curb pollution [4]. The utilization of various non-conventional energy sources along with integrated energy storage systems is the need of the hour [5]. Scientists are exploring various techniques to enhance the efficiency of renewable energy systems. Some researchers are trying to enhance the performance of biofuel [6], and others are utilizing solar energy for energy storage systems [7,8,9,10]. The modification of wind power systems is also being explored [11]. Despite solar photovoltaics having a wide energy generation share, fossil fuels are still predominantly favored because of the comparatively lower photovoltaic conversion efficiencies. Solar cell photoelectric conversion efficiency is affected by the absorption and reflection of photons at its top surface.
Numerous methods have been explored to modify the morphology of the top layer to attain maximum absorption and minimize reflection. Surface texturing is an effective method to minimize light reflection and modify optical transitions [12]. Due to the texturized surface, when incident light follows a non-perpendicular trajectory, multiple reflections may occur in the absorber layer [13]. The oblique incidence of light rays at the front surface creates a light-trapping effect. This oblique propagation of light rays not only helps to increase the path length but also enhances the chances of re-reflection due to the phenomenon of total internal reflection [14]. The angular inclination and thickness of the textured layer can be regulated to obtain optimum performance from a solar cell.
Nonetheless, the predicament with these enhancement techniques is that they are either time-intensive or costly. As an alternative, modeling and simulating the system’s performance using various software as simulation tools has emerged as an optimistic solution. During the previous decade, numerous scientists have investigated the modeling of photovoltaic (PV) cell technology using a variety of simulation and modeling software. Kumar et al. (2020) evaluated current voltage and power voltage characteristics by partial shading using the MATLAB/Simulink (R2020a) environment [15]. Waseem et al. (2021) simulated a photovoltaic power plant in PVsyst 6.8 software [16]. Yadav et al. (2021) compared Si and Ge solar cell electrical characteristics using PC1D [17]. Hashmi et al. (2018) experimented with modifying various parameters on a solar cell through PC1D simulation [18]. Texturing the top (front-to-light incidence) surface of a solar cell is an important process to enhance the optical path length of the Sun’s rays inside the solar cell. It not only increases the surface area for light incidence but also reduces front surface reflection due to light trapping. Hence, it is imperative to design optimal thickness and slope for the texturing. This work concentrates on the effect of changes in surface texturing depth and inclination using PC1D simulation. Electrical parameters like PV efficiency (η) values, fill factor (FF) values, open circuit voltage (VOC) values, and short circuit current (ISC) values were tested through simulation.
2. Design of the Model
A solar PV cell with a thin N-type emitter layer and a hilly textured surface was designed using PC1D software. It has a front surface area of 200 cm2 and a thickness of 200 µm and features series and shunt resistance. In Figure 1, the solar PV cell designed in PC1D is shown with an initial texture depth of 1 µm and a front surface reflectance of 30% at a 50° inclination. The simulation was conducted using an air mass code of AM1.5 and 1000 W/m2 constant light intensity. The base contact resistance was set to 0.15 Ω, while the internal conductance was 0.3 S. Table 1 shows the values of the Si parameters used in the simulation, where the test temperature was set at 25 °C and the carrier excitation was frequency set to 20 steps.
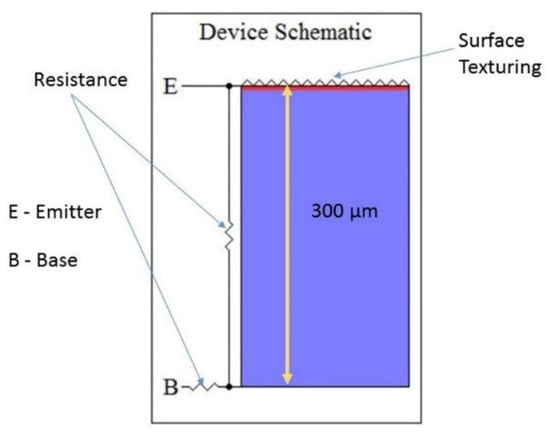
Figure 1.
Schematic of solar cell.

Table 1.
Parameters for silicon.
3. Results and Discussion
3.1. Surface Texturing of 0.5 µm Depth
Figure 2 depicts the I-V and P-V curves of the designed solar cell model with a 0.5 µm thick surface texturing depth at angles of 50°, 55°, 60°, 65°, and 70°. The highest VOC of 0.62617 V was obtained at 50°, while the highest ISC value of 6.341 A was obtained at 70°. The highest FF value of 0.724067 was attained at 50°, while the highest η value of 0.135866 was obtained at 70°. As the slope of texturing increases, the value of ISC also increases. This is attributed to the more incident light trapping in the PV cell resulting in more carrier generation. Due to the same phenomena, VOC was decreasing with an increased slope.
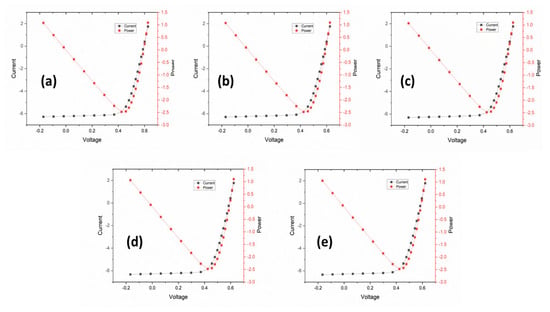
Figure 2.
I−V curves of 0.5 µm thick surface texture and angles of (a) 50°, (b) 55°, (c) 60°, (d) 65°, and (e) 70°.
3.2. Surface Texturing of 1.0 µm Depth
Figure 3 depicts the I-V and P-V curves of the designed solar cell model with a 1 µm thick surface texturing depth at angles of 50°, 55°, 60°, 65°, and 70°. The highest VOC of 0.62562 V was obtained at 50°, while the highest ISC value of 6.4377 A was obtained at 70°. The highest FF value of 0.723673 was attained at 55°, while the highest η value of 0.136215 was obtained at 65°. The VOC decreased, but the ISC increased more than the values for 0.5 µm depth. The increase in texture thickness leads to more light trapping.
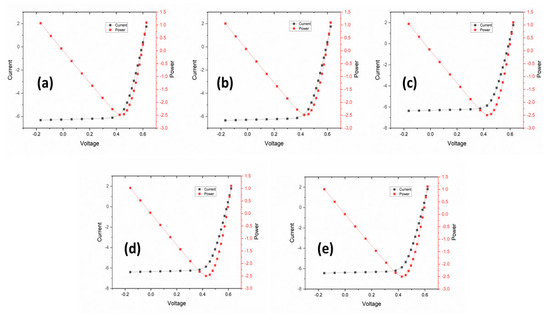
Figure 3.
I−V curves of 1 µm thick surface texture and angles of (a) 50°, (b) 55°, (c) 60°, (d) 65°, and (e) 70°.
3.3. Surface Texturing of 1.5 µm Depth
Figure 4 depicts the I-V and P-V curves of the designed solar cell model with a 1.5 µm thick surface texturing depth at angles of 50°, 55°, 60°, 65°, and 70°. The highest VOC of 0.62545 V was obtained at 50°, while the highest ISC value of 6.4569 A was obtained at 70°. The highest FF value of 0.72439 was attained at 60°, while the highest η value of 0.136648 was obtained at 60°. Here, also a similar trend for VOC and ISC was obtained.
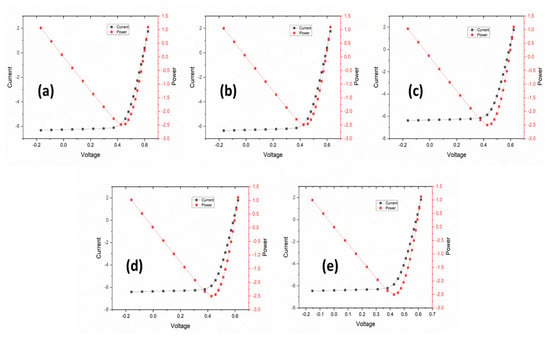
Figure 4.
I−V curves of 1.5 µm thick surface texture and angles of (a) 50°, (b) 55°, (c) 60°, (d) 65°, and (e) 70°.
3.4. Surface Texturing of 2.0 µm Depth
Figure 5 depicts the I-V and P-V curves of the designed solar cell model with a 2 µm thick surface texturing depth at angles of 50°, 55°, 60°, 65°, and 70°. The highest VOC of 0.62537 V was obtained at 50°, while the highest ISC value of 6.4648 A was obtained at 70°. The highest FF value of 0.724066 was attained at 50°, while the highest η value of 0.136609 was obtained at 60°. An increase of 300% in texture thickness also provided a higher amount of light trapping, which can be seen from higher values of ISC.
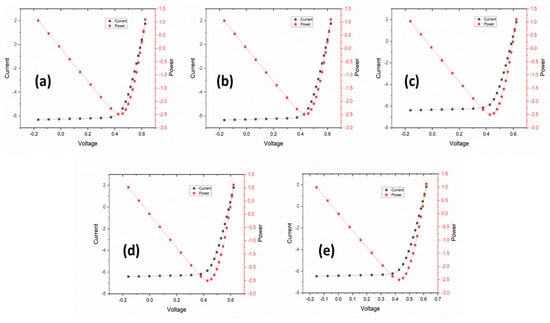
Figure 5.
I−V curves of 2 µm thick surface texture and angles of (a) 50°, (b) 55°, (c) 60°, (d) 65°, and (e) 70°.
3.5. Surface Texturing of 2.5 µm Depth
Figure 6 presents the I-V and P-V curves of the designed solar cell model with a 2.5 µm thick surface texturing depth at angles of 50°, 55°, 60°, 65°, and 70°. The highest VOC of 0.62532 V was obtained at 50°, while the highest ISC value of 6.474 A was obtained at 70°. The highest FF value of 0.724062 was attained at 50°, while the highest η value of 0.136745 was obtained at 60°. Here, a similar trend was observed, but the change in the values of VOC and ISC was not significant. This shows that above a certain texture thickness, it acts as light shading instead of a light-trapping structure. Hence, the surface texture thickness needs to be optimized during PV cell design.
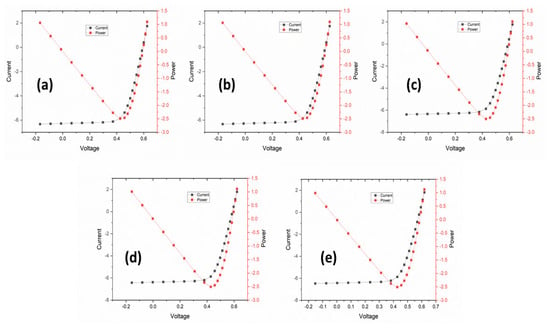
Figure 6.
I−V curves of 2.5 µm thick surface texture and angles of (a) 50°, (b) 55°, (c) 60°, (d) 65°, and (e) 70°.
The below readings in five different parameters show that as the angle increases above 50°, the FF keeps on decreasing until 65° is reached, but it drops to 70°. As for the efficiency, a reverse trend was observed. As the thickness of the texture increases from 1 µm to 5µm, the efficiency first decreased for 2 µm and then increased for 3 µm and 4 µm, and then it declined to 5 µm. This shows that when the thickness is increased, then the formed trough traps more light entering into it, but after a certain point, the amount of light entering the trough is also reduced. Therefore, the texture thickness should be properly optimized. Also, Hashmi et al. [19] performed an optimization of surface texturing, anti-reflective coating, and p-type and n-type doping to obtain an efficiency improvement of nearly 2%. In the present work, by optimizing only surface texturing, efficiency was enhanced by 0.64%.
4. Analysis Using COMSOL
This section presents the analysis of the PV system using COMSOL 6.0. The surface texturing forms pyramid-shaped surfaces on the PV, which traps most of the light and reflects internally, which in turn improves the performance parameters of the solar cell. Figure 7 depicts the simulation of the heat transfer in a PV solar cell at room temperature.
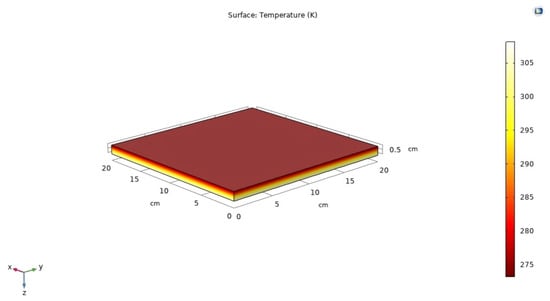
Figure 7.
Surface temperature.
In COMSOL, a rough surface is formed to analyze the absorption of heat and light. In this dimension, x and y remain at 1 cm and the surface roughness using the mathematical equation. In actual practice, texturing is performed by etching or using photolithographic methods. This forms a pyramid-like structure which helps in absorbing the heat and light energy. The dimension of the z surface is given by varying the value of W in the equation, which indicates surface roughness. When the angle of W decreases, the surface roughness increases. The simulation of a rough surface silicon block is shown in Figure 8. The parametric surface equation used is given below.
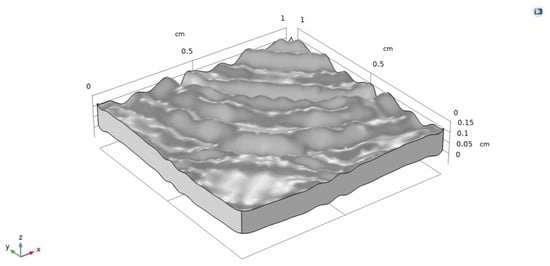
Figure 8.
Solar cell with rough texture.
Figure 9 indicates that after introducing the rough texture, heat and light absorption is increased compared to the flat surface. This can be further analyzed with the coating of different materials, and a suitable coating is used to improve the efficiency of the PV system.
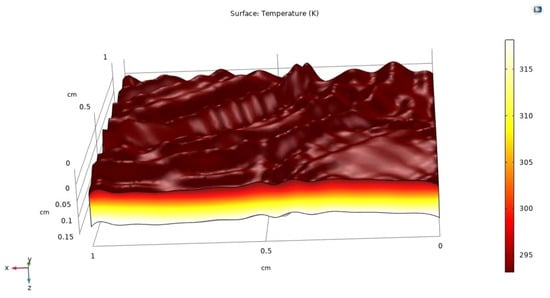
Figure 9.
PV cell after surface texturing.
5. Conclusions
This research presents a simulation on the PC1D tool to analyze the effect of varying the surface texture thickness and texture angle on the electrical performance parameters of a solar PV cell. An opensource PC1D software simulation tool was used for the PV analysis. Readings were taken by changing the surface texture angle to five values of 50°, 55°, 60°, 65°, and 70°. Also, there were five different texture thicknesses of 1 µm, 2 µm, 3 µm, 4 µm, and 5 µm. It was noticed that for a solar cell of a 100 cm2 cross-sectional area, the optimum texture thickness is 3 µm with a texture angle of 60°.
Author Contributions
Conceptualization, A.Y. and S.R.P.; methodology, A.Y.; software, A.Y. and S.R.P.; validation, A.Y. and S.R.P.; writing—original draft preparation, A.Y.; writing—review and editing, A.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- REN21. Renewables 2019 Global Status Report. 2019. Available online: https://wedocs.unep.org/handle/20.500.11822/28496 (accessed on 23 May 2020).
- Tvaronavičienė, M.; Baublys, J.; Raudeliūnienė, J.; Jatautaitė, D. Global energy consumption peculiarities and energy sources: Role of renewables. In Energy Transformation Towards Sustainability; Elsevier: Amsterdam, The Netherlands, 2020; pp. 1–49. [Google Scholar]
- Vaishak, S.; Bhale, P.V. Photovoltaic/thermal-solar assisted heat pump system: Current status and future prospects. Sol. Energy 2019, 189, 268–284. [Google Scholar] [CrossRef]
- Solorio, I.; Jörgens, H. Contested energy transition? Europeanization and authority turns in EU renewable energy policy. J. Eur. Integr. 2020, 42, 77–93. [Google Scholar] [CrossRef]
- Rekioua, D. Storage in Hybrid Renewable Energy Systems. In Hybrid Renewable Energy Systems; Springer: Cham, Switzerland, 2020; pp. 139–172. [Google Scholar]
- Kumar, S.; Yadav, A. Comparative experimental investigation of preheated thumba oil for its performance testing on a CI engine. Energy Environ. 2018, 29, 533–542. [Google Scholar] [CrossRef]
- Kumar, V.; Dhasmana, H.; Yadav, A.; Kumar, A.; Verma, A.; Bhatnagar, P.K.; Jain, V.K. Theoretical analysis of temperature-dependent electrical parameters of Si solar cell integrated with carbon-based thermal cooling layer. In Advances in Solar Power Generation and Energy Harvesting; Springer: Singapore, 2020; pp. 27–36. [Google Scholar]
- Safaei, M.R.; Goshayeshi, H.R.; Chaer, I. Solar still efficiency enhancement by using graphene oxide/paraffin nano-PCM. Energies 2019, 12, 2002. [Google Scholar] [CrossRef]
- Yadav, A.; Verma, A.; Bhatnagar, P.K.; Jain, V.K.; Kumar, V. Enhanced thermal characteristics of ng based acetamide composites. Int. J. Innov. Technol. Explor. Eng. (IJITEE) 2019, 8, 4227–4231. [Google Scholar] [CrossRef]
- Chauhan, S.; Singh, B. Control of solar PV-integrated battery energy storage system for rural area application. IET Renew. Power Gener. 2021, 15, 1030–1045. [Google Scholar] [CrossRef]
- Rekioua, D. Hybrid Renewable Energy Systems Overview. In Hybrid Renewable Energy Systems; Springer: Cham, Switzerland, 2020; pp. 1–37. [Google Scholar]
- Ackermann, J.; Videlot, C.; El Kassmi, A. Growth of organic semiconductors for hybrid solar cell application. Thin Solid Film. 2002, 403, 157–161. [Google Scholar] [CrossRef]
- Carson, J.A. (Ed.) Solar Cell Research Progress; Nova Publishers: New York, NY, USA, 2008. [Google Scholar]
- Luque, A.; Mellor, A.V. Photon Absorption Models in Nanostructured Semiconductor Solar Cells and Devices; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Kumar, D.; Mishra, P.; Ranjan, A.; Dheer, D.K.; Kumar, L. A Simplified Simulation Model of Silicon Photovoltaic Modules for Performance Evaluation at Different Operating Conditions. Optik 2020, 204, 164228. [Google Scholar] [CrossRef]
- Waseem, N.; George, A.S.; Hameed, S.; Yadav, A.; Pillai, S.R.; Shukla, V.K. Simulation of a Dubai Based 100 KW Solar Plant on PVsyst. In Proceedings of the 9th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions) (ICRITO), Noida, India, 3–4 September 2021; IEEE: Toulouse, France, 2021; pp. 1–5. [Google Scholar]
- Yadav, A.; Yadav, H.; Vashishtha, V.K.; Shivhare, M.K. Comparative performance evaluation of Si and Ge solar cell using PC1D modelling. In Recent Advances in Mechanical Engineering; Springer: Singapore, 2021; pp. 199–205. [Google Scholar]
- Hashmi, G.; Akand, A.R.; Hoq, M.; Rahman, H. Study of the enhancement of the efficiency of the monocrystalline silicon solar cell by optimizing effective parameters using PC1D simulation. Silicon 2018, 10, 1653–1660. [Google Scholar] [CrossRef]
- Hashmi, G.; Rashid, M.J.; Mahmood, Z.H.; Hoq, M.; Rahman, M.H. Investigation of the impact of different ARC layers using PC1D simulation: Application to crystalline silicon solar cells. J. Theor. Appl. Phys. 2018, 12, 327–334. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).