Extended Object Tracking Performance Comparison for Autonomous Driving Applications ^†

Abstract

Extended object tracking is crucial for autonomous driving, as it enables vehicles to perceive and respond to their environment accurately by considering an object’s shape, size, and motion over time. Two commonly used methods for extended object tracking, Joint Probabilistic Data Association (JPDA) and Gaussian Mixture Probability Hypothesis Density (GM-PHD), were compared in autonomous vehicles using radar data. Both JPDA and GM-PHD perform well in tracking multiple extended objects, but GM-PHD demonstrates a performance advantage, especially in terms of the Generalized Optimal Sub-Pattern Assignment (GOSPA) metric, which measures the accuracy of tracked object positions in comparison to their actual positions.

1. Introduction

Radar technology has revolutionized the way that information is gathered about the surrounding environment, providing valuable insights into the movement and position of objects. One of the most important applications of radar technology is extended object trackers (EOTs), which are sophisticated systems that enable the detection and tracking of multiple objects simultaneously.

An EOT is a critical component of many modern systems, including air traffic control, weather monitoring, and autonomous driving systems. By using advanced algorithms and sophisticated hardware, these systems can accurately identify and track the position, speed, and direction of objects in real time, even in challenging weather conditions. The main aims of an EOT are to track the kinematics and estimate the size of the objects nearby the ego vehicle [1]. As per [2], the shape is often assumed to be rigid, i.e., non-changing. Tracking an extended object is in general a highly complex problem due to the non-linearity of the resulting estimation problem.

Various tracking algorithms have been developed for EOTs. One popular approach is the multi-hypothesis tracking (MHT) algorithm [3], which generates multiple hypotheses about the object’s position and shape based on measurements. Another approach is the JPDA algorithm [4], which assigns probabilities to each measurement–object association and updates the probabilities over time. More recently, deep-learning-based object detectors have been proposed, such as the CenterNet [5] and YOLO [6] algorithms, which use convolutional neural networks to predict the object’s position and size.

One notable work in this area is the method proposed by Granström et al. [7], who proposed a probabilistic approach to extended object tracking based on the concept of random matrices. Their method also uses a Bayesian filter to estimate the object’s state and shape, and it was shown to be effective in tracking vehicles in cluttered environments. Another approach was presented by Ba-Ngu Vo and Wing-Kin Ma [8], who propose a GM-PHD filter for extended object tracking. Their method uses the probability hypothesis density to represent the object’s state and shape and was shown to be effective in tracking multiple objects with varying shapes and sizes.

In this paper, two methods are compared for the purpose of extended object tracking, which are JPDA and GM-PHD. The main reason for comparing these two algorithms here is to see which algorithm’s results are at the desired level and to determine the algorithm we will use in real-time applications in the future. Both algorithms are coded in the MATLAB environment. The Driving Scenario Designer Toolbox [9] in MATLAB is used to test the implemented algorithms. The created scenarios include an ego vehicle and three surrounding vehicles. Measurements are taken from the radar on the ego vehicle, and the designed algorithms are executed and compared with ground truth data.

The remainder of this paper is structured as follows. Firstly, details of both algorithms are explained, then the Generalized Optimal Sub-Pattern Assignment metric, which is defined for comparison, is given. Finally, the simulation system and results are presented and future work is discussed.

2. Extended Object Tracking

2.1. Joint Probabilistic Data Association Tracker

The JPDA algorithm is a statistical approach used to solve the problem of data association in multiple target tracking [4]. The problem of data association involves assigning observations to a set of targets, where the observations are potentially noisy.

The JPDA algorithm considers all possible combinations of the observations and targets and computes the probability of each association based on the likelihood of the observations given the targets, as well as the prior probability of each target being present. These probabilities are then combined using Bayes’ rule to obtain the posterior probability of each target being associated with each observation.

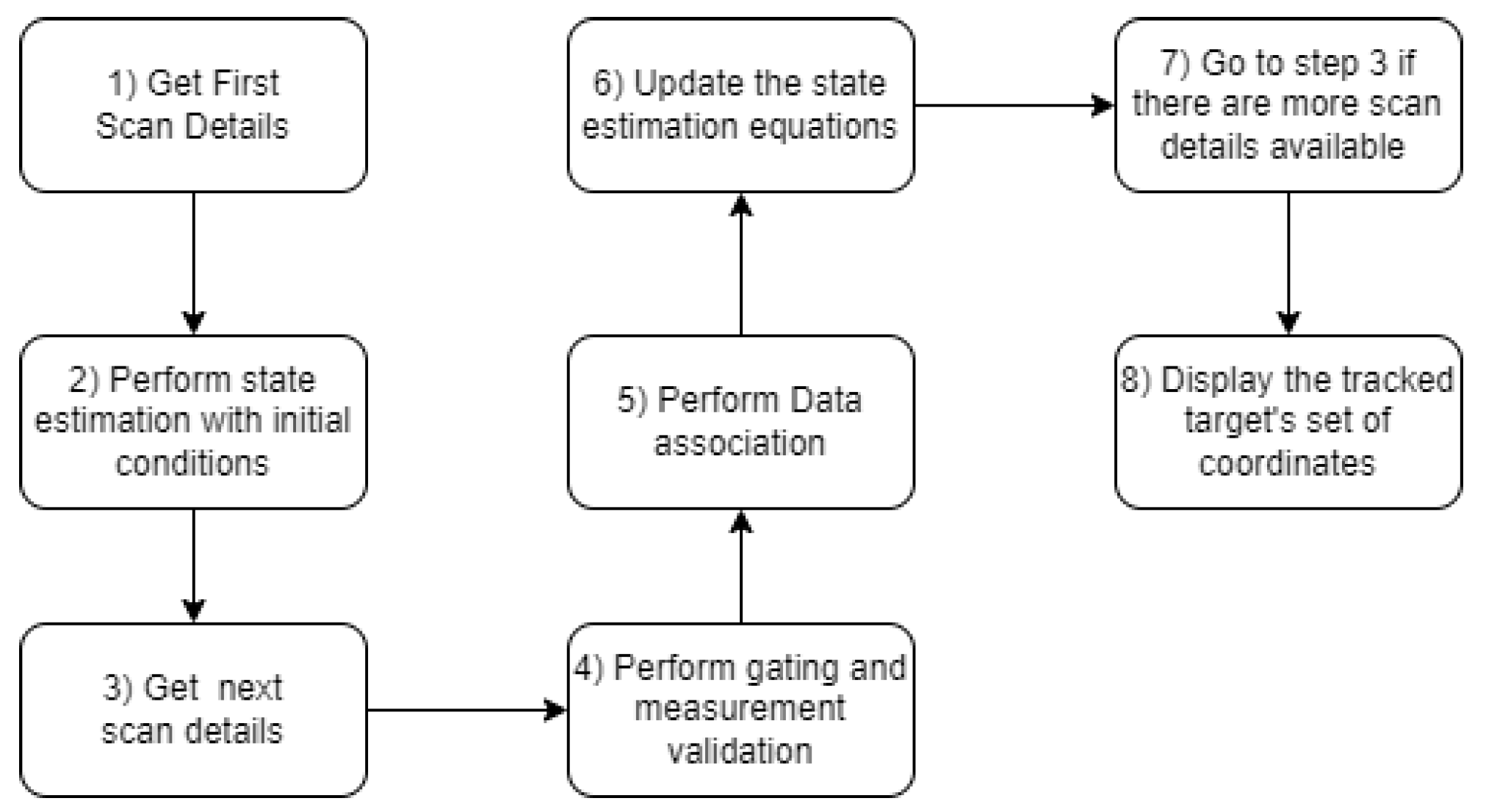
The JPDA tracker is an implementation of the JPDA algorithm for multiple target tracking. The main steps of the algorithm are summarized as follows:

• Initialization: Initialize the target states and their associated covariances and set the prior probabilities of each target being present.
• Prediction: Predict the state and covariance of each target based on a motion model and update the prior probabilities of each target being present.
• Data Association: Compute the likelihood of each observation given each target, and use the JPDA algorithm to compute the posterior probability of each target being associated with each observation
• Track Update: Update the state and covariance of each target based on the associated observations and compute the likelihood of each track.
• Track Management: Decide whether to create a new track for an unassociated observation or terminate a track if its likelihood falls below a certain threshold.

The general structure of the JPDA filter flowchart is shown in Figure 1.

2.2. Gaussian Mixture Probability Hypothesis Density Filter

The GM-PHD filter is a Bayesian filtering algorithm that is commonly used for multiple target tracking. It is an extension of the probability hypothesis density (PHD) filter, which is a non-parametric approach to multi-target tracking that represents the state of the targets using a single probability density function.

The GM-PHD filter extends the PHD filter by modeling the probability density function of the targets as a mixture of Gaussian components. Each Gaussian component corresponds to a potential target, and its mean and covariance represent the state and uncertainty of the target.

The GM-PHD filter consists of two main steps: prediction and update.

• Prediction: The means and covariances of the Gaussian components are propagated using a motion model. The weights of the Gaussian components are also updated based on the predicted probability of each target being present.
• Update: The filter incorporates the measurement information by calculating the likelihood of each measurement given each Gaussian component. The weights of the Gaussian components are then updated based on the likelihood and the predicted probability of each target being present.

The GM-PHD filter is efficient and scalable, as it can handle a large number of targets and clutter measurements. It also provides a probabilistic representation of the estimated target states, which can be used for decision making and sensor fusion. The general structure of the GM-PHD filter flowchart is shown Figure 2.

3. Comparison Metric

The GOSPA metric was proposed by Rahmathullah et al. [10] as a way to evaluate the performance of extended object tracking algorithms. The metric compares the estimated and true object trajectories and provides a quantitative measure of the tracking accuracy. It is a generalization of the Optimal Sub-Pattern Assignment (OSPA) metric that considers not only the distances between individual detections/tracks, but also the cardinality differences between the sets being compared.

The GOSPA metric measures the similarity between two sets of detections/tracks based on the distances between their individual elements, as well as the number of false alarms and missed detections. The metric is defined by four parameters: p, c, $\alpha$, and $\beta$. The parameter p determines the order of the distance metric used to compare individual detections/tracks (e.g., p = 2 corresponds to the Euclidean distance). The parameters c, $\alpha$, and $\beta$ control the trade-off between the cardinality differences and the distances between the sets.

The GOSPA metric is a useful tool for evaluating the performance of multiple object tracking algorithms, as it provides a comprehensive measure of their accuracy and robustness. The code structure of the GOSPA algorithm is detailed in Algorithm 1 briefly.

4. Simulation System and Results

4.1. Simulation System

The MATLAB environment was used as the simulation system. Both the JPDA tracker and GM-PHD algorithm were implemented in the MATLAB environment. The implemented algorithms were tested with radar data obtained from Driving Scenario Toolbox. The studies were carried out on a single radar dataset on the ego vehicle. In the tested scenarios, the number of vehicles in the environment is fixed.

In order to provide more reliable measurement values from surrounding vehicles to the algorithm and to make more accurate decisions about which measurement belongs to which vehicle, a clustering algorithm was applied to the obtained radar measurements. The clustering algorithm was selected as Density-Based Spatial Clustering of Applications with Noise (DBSCAN) [11]. This clustering algorithm takes two parameters as input along with the incoming measurement values. These two parameters are a radius value $ϵ$ and the minimum number of points required to form a dense region (minPts). In the simulations, $ϵ$ was taken as 20 and minPts was taken as 3.

The simulation scenario was created in Driving Scenario Designer Toolbox [9]. In this scenario, the vehicles around the ego vehicle do not only move on a straight road. To increase the complexity of the scenario, lane changes were introduced and the vehicles were brought closer together. In the next section, the implementation of both JPDA and GM-PHD algorithms to the simulation system and the results obtained are shown.

4.1.1. JPDA Tracker

In this section, the JPDA tracker algorithm, which is explained in Section 2.1, is implemented in the MATLAB environment. Studies are carried out on a single radar dataset on the ego vehicle.

A covariance ellipse was created by using the velocity and position of the ego vehicle with the radar data. These created ellipses are also shown in Figure 3. The parameters used in the JPDA tracker algorithm and ellipse generation and their definitions are shown in

Table 1. JPDA parameters.

Symbol	Definition
$C_v$	Measurement Noise Covariance
$C_{rw}$	Error Covariance for Kinematic State
$A_r$	Transition for Kinematic State
$A_p$	Transition for Shape Parameters
$C_r$	Pos x,y and Vel x,y Covariance Matrix
$C_p$	Major and Minor Axes and Azimuth Angle of Ellipse

. Initial values of these parameters are given as follows.

$$\begin{array}{c}{C}_v=\mathrm{diag}(10,10),\hspace{1em}{C}_{rw}=\mathrm{diag}(10,10,1,1),\\ A_p=\mathrm{diag}(1,1,1),\hspace{1em}{C}_r=\mathrm{diag}(0.3,0.3,0.1,0.1)\\ A_r=\left[\begin{array}{cccc}1& 0& 0.05& 0\\ 0& 1& 0& 0.05\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right],\\ C_p=\mathrm{diag}(0.2,0.1,0.1)\end{array}$$

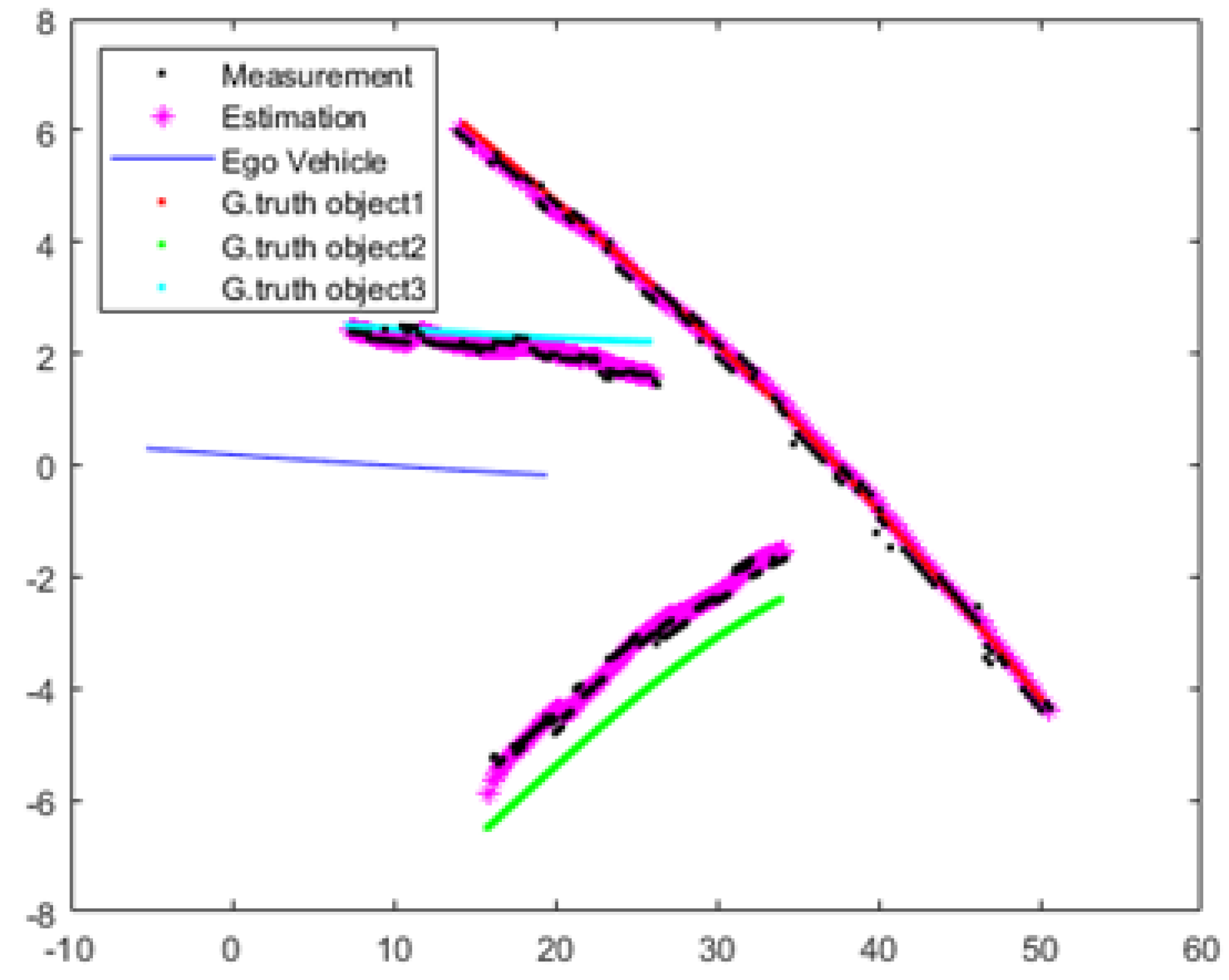
When observing Figure 3, it can be seen that the position estimations of the vehicles surrounding the ego vehicle are quite close to the ground truth data. However, it is observed that the errors in position estimation begin to increase as the vehicles move closer to each other. When the vehicles are close to each other, the data association part can be a problem due to the distinguishing part.

4.1.2. GM-PHD

In this section, the GM-PHD algorithm, which is explained in Section 2.2, is implemented in the MATLAB environment. Studies are carried out on a single radar dataset on the ego vehicle. The data used here are the same as the data used in the JPDA algorithm. Some of the parameters and their definitions are shown in

Table 2. GM-PHD parameters.

Symbol	Definition
$v_{sigma}$	Q noise matrix amplitude
$P_s$	Survival probability
$P_d$	Probability of detection
$w_{birth}$	Weighting of birth terms
$m_{birth}$	Mean of birth terms
$P_{birth}$	Covariance of birth terms

. The initial values of these parameters are also given as follows.

$$\begin{array}{c}{v}_{sigma}=1,\hspace{1em}{P}_s=0.99,\hspace{1em}{P}_d=0.99\\ w_{birth}=0.99,\hspace{1em}{P}_{birth}=\mathrm{diag}(1,1,1,1)\\ m_{birth}=\left[\begin{array}{ccc}14.400& 15.800& 7.200\\ 5.832& 2.901& 2.999\\ 6.100& -6.500& 2.500\\ -1.407& 0.7636& -0.057\end{array}\right]\end{array}$$

When observing Figure 4, it can be seen that the position estimations of the vehicles surrounding the ego vehicle are quite close to the ground truth data. It can be observed that even when vehicles approach each other, the predictions do not shift to other vehicles. It can easily be said that the data association part works more effectively in the GM-PHD algorithm when compared with Figure 3 and Figure 4.

4.2. Performance Comparison of JPDA and GM-PHD Algorithms

The results obtained in Section 4.1.1 and Section 4.1.2 qualitatively illustrate the good performance of both algorithms. However, we need a quantitative metric which shows the accuracy of the performance of each algorithm. The GOSPA metric defined in Section 3 is used to illustrate the tracking performance of the JPDA and GM-PHD algorithms. Based on their values (the performance improves as the GOSPA value decreases), the performances of the algorithms are compared. The parameters p and c were chosen to be 2 and 100, respectively. 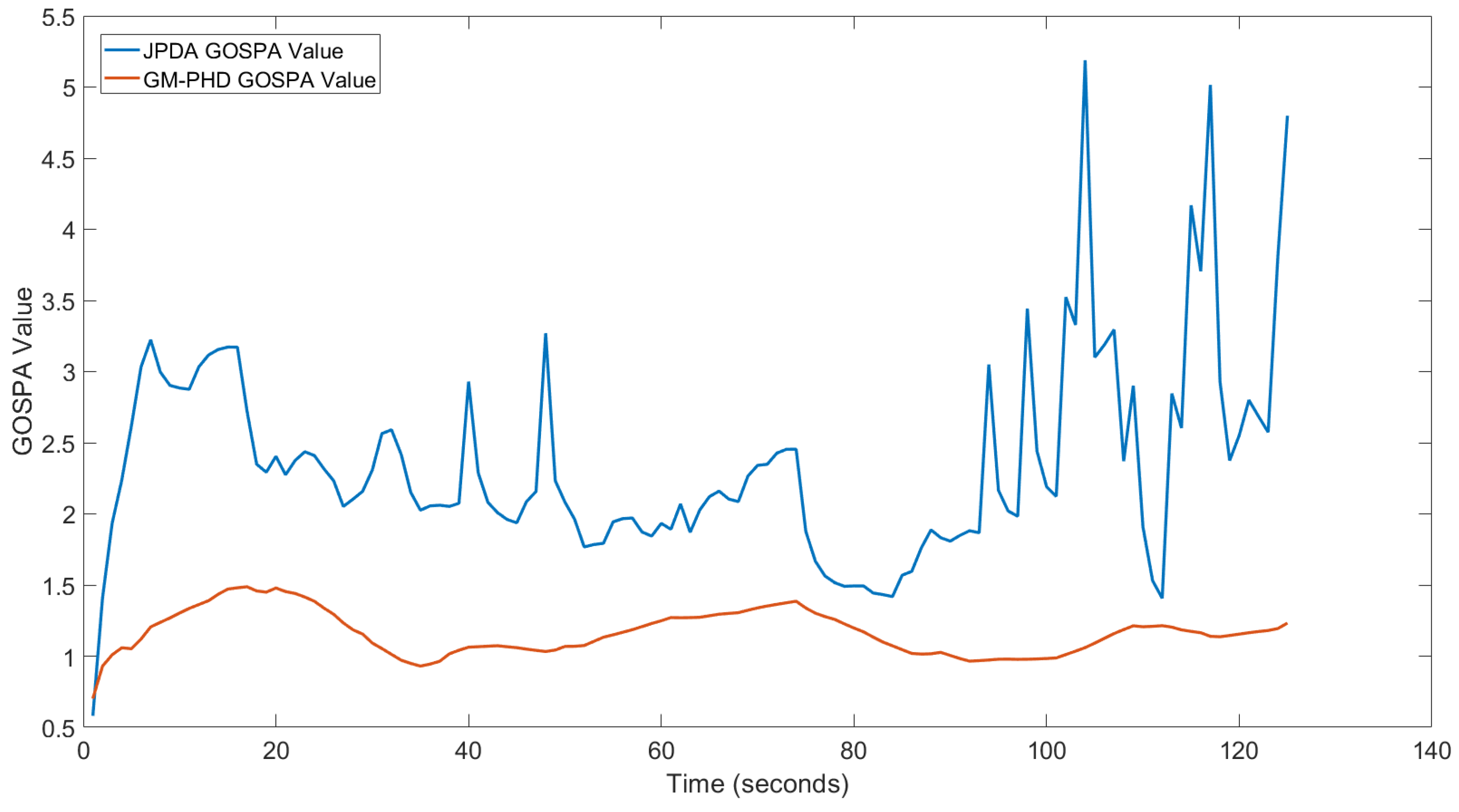Figure 5 illustrates the comparison of GOSPA values for the tracking performance of JPDA and GM-PHD algorithms.

The GOSPA value comparison illustrates that both algorithms are good at keeping track of the surrounding objects. For both of them, the GOSPA values are quite low. It can be seen that the GOSPA values obtained with GM-PHD are much lower than those obtained with JPDA. The GOSPA values oscillate between 1 and 1.5 for GM-PHD, whereas the GOSPA values obtained with JPDA vary between 1.5 and 5. In brief, the GOSPA results quantitatively illustrate that the tracking performance of GM-PHD is superior to JPDA.

5. Conclusions

In this paper, JPDA and GM-PHD methods are compared with each other for the purpose of extended object tracking. Both methods have advantages and disadvantages with respect to each other. In autonomous driving applications, there is no study which compares the performance of both methods based only on radar data. The GOSPA metric was chosen to compare the performance of GM-PHD and JPDA. The simulation platform was chosen to be the MATLAB Driving Toolbox.

The simulation results show that both algorithms are good at keeping track of the surrounding vehicles, which is understood from the low GOSPA values at all time stamps of the simulation. It is also clearly observed that the GOSPA values obtained with GM-PHD are much lower than the GOSPA values obtained with JPDA, which shows the superiority of GM-PHD over JPDA based on performance. Although it is known that GM-PHD is able to keep track of the objects when the number of objects is varied, unlike JPDA, GM-PHD is not optimal to estimate the cardinality of the objects when the newborn object is modeled as static and not measurement-driven. In the future, we aim to keep track of the surrounding objects by using the adaptive-birth GM-PHD algorithm in real-time implementations for autonomous driving applications.