Sensitivity Analysis of Internally Reinforced Beams Subjected to Three-Point Bending Load ^†

Abstract

This work focused on the study of efficient solutions for the improvement of the mechanical behavior and movement capability of industrial devices with mobile parts subjected to three-point bending load. To achieve the aim of developing efficient engineering solutions, several stages were followed. A sensitivity analysis was conducted on one of the beams in order to determine the influence of each variable in the mass and in the displacement’s parameter space. It has been shown that parameterizing the ANSYS input file is effective for finding out how sensitive the system is to the design variables studied. The results of the sensitivity analysis may be used in the future to choose the variable weights that will be used in optimization techniques and processes. Further study might be performed in the future to attempt to find a way to generalize the methodology for different models and/or in different situations.

1. Introduction

In numerous applications involving industrial apparatus, the load accelerates electrically motor-driven moving components. These actuators accelerate twelve times more rapidly than gravity. Acceleration necessitates structures that are more rigid and robust. Stiffness influences equipment efficacy more than strength. Accelerations can cause equipment deflection and output reduction. Increased vibrations may lead to complications. Geometric optimization increases stiffness more so than material selection. Geometry may increase the stiffness of a burden. The combination of mass and deflections is more effective than deflections alone. By reducing the size of industrial machinery with movable components, it is possible to increase their speed without diminishing their mechanical performance. Because thin-walled structures can be reinforced internally and have high effectiveness by mass unit, hollow solid sections present advantages in engineering applications in relation to their bulk counterparts, with the same outer section dimension and section shape. Similar beams to the one presented herein were already studied in terms of their mechanical behavior in [1].

Engineering structures like plates and casings need to be stiff—the stiffness in form of the ribbed, webbed, and curved walls is the typical solution. This objective necessitates the previous two. Ribs and webbing provide reinforcement for thin-walled components [2]. Orlov states that ribs increase the moment of inertia and strength [2]. Few studies have examined structural steel’s stiffening. These aircraft structures, which have been in use since the beginning of the 20th century, may have been investigated in the past [3]. Vieira and colleagues investigated the mechanics of structural stiffening. This effort could benefit from the author’s design [4]. Thin-walled steel columns reinforced by Liu increase their bending and torsion strength without increasing their weight [5]. Steel beam dynamics are influenced by transverse ribs [6]. Under various load regimens, the same author evaluated the spatial stability of rib-reinforced thin-walled beams. Differential equations were solved by orthogonalization of Bubnov–Galerkin. Problems were resolved by analyzing and substantiating circumstances. Eigenvalue problems were transformed from general solutions. Experiments confirmed the validity of the method. It is computed [7]. Liu and Gannon welded plates to a loaded W-shaped steel girder. Reinforcement patterns, welding preload magnitudes, and unreinforced beam defects were modeled using the Finite Element Method [8]. In [9], the type, size, and location of stiffeners were proposed. This effort improves the mechanical performance of thin-walled beams by adding ribs, lattice, and sandwich panels to rectangular hollow-box beams.

2. Materials and Methods

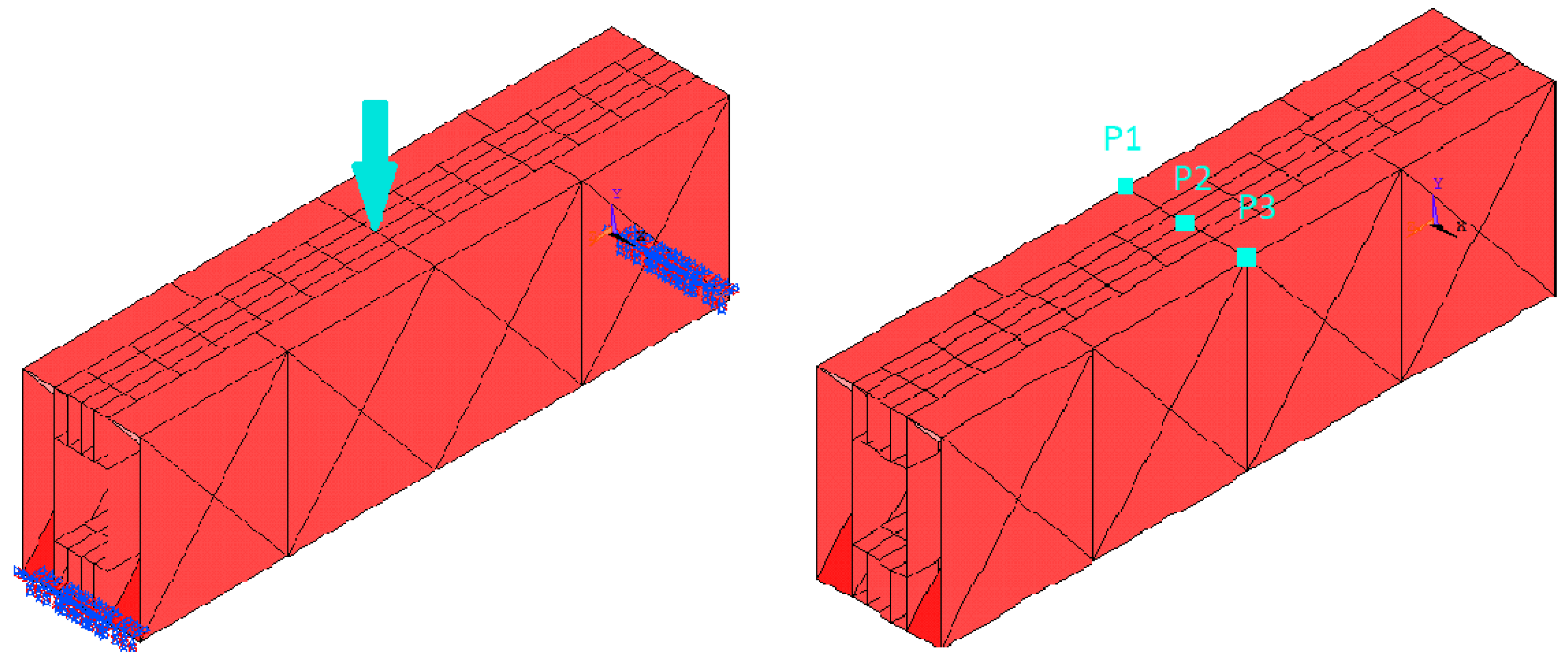
Sensitivity analysis utilized a single Finite Element Model (FEM) model. The FEM model with applied loading and degrees of freedom (DOF) constraints is depicted in Figure 1 (left). Several keypoints were selected to depict the data presented in this article, as shown in Figure 1 (right).

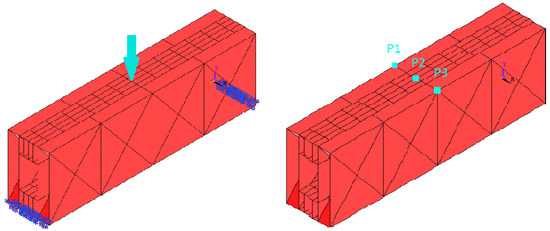
Figure 1. Applied load and DOF constraints (left); points used to calculate displacements on sensitivity analysis procedure (right), adapted from [1].

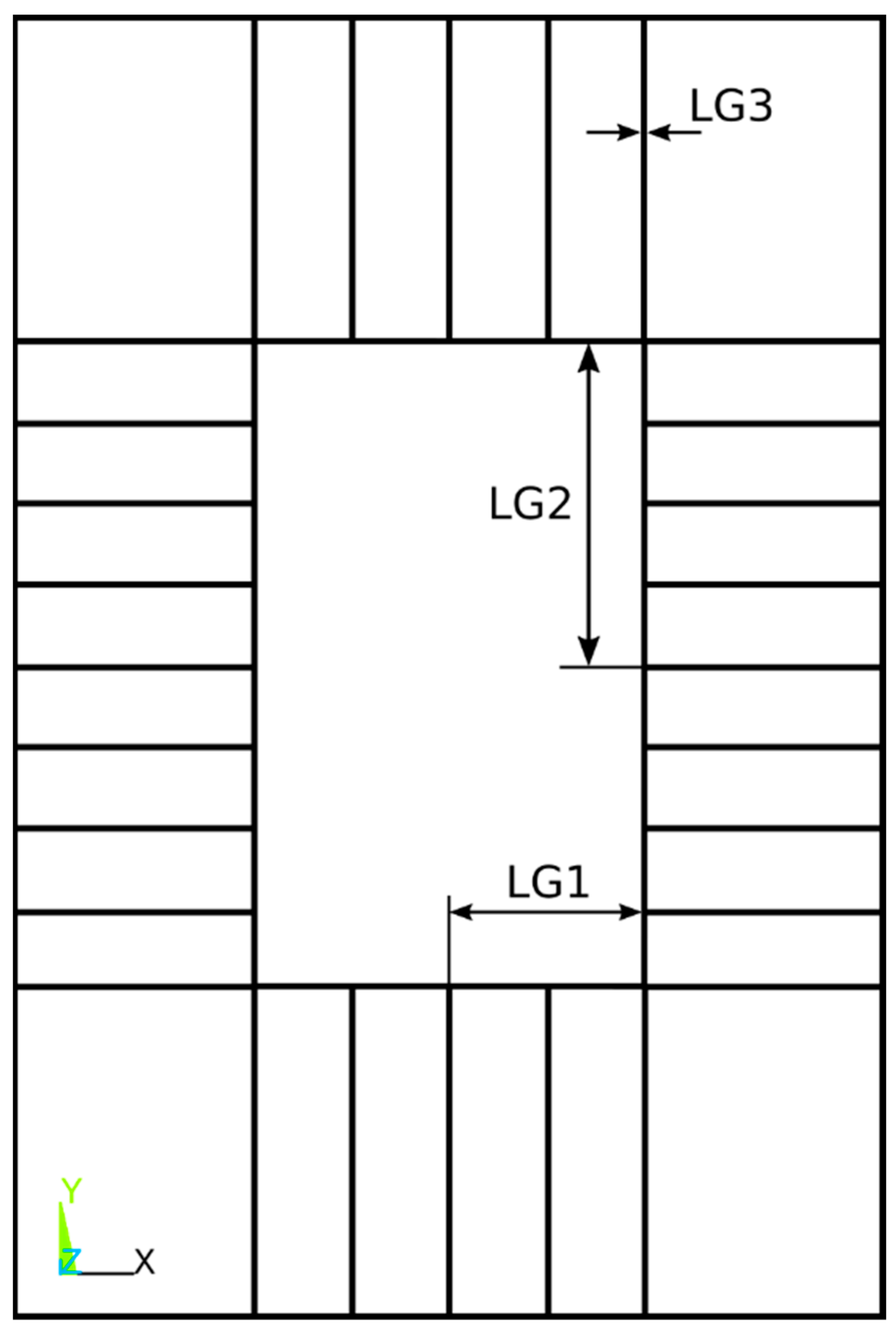
These keypoints were chosen because their coordinates are unaffected by a change in the variable values during optimization. As these areas are extensively reinforced with ribs, it is not anticipated that the thin material at the under-consideration thicknesses can result in significant local deformation. This was demonstrated by analyzing large deformation in terms of geometrical nonlinearity. The outcome was identical to that of a linear static analysis. Providing an analysis falls outside the scope of this endeavor at this time. During the evaluation of the thickness variable LG3, values between 2 and 4 mm were considered. The thickness remained unchanged at 3 mm in all other instances. Clearly, the laterals have a greater effect on the results than the initial beams subject to torsion stresses. The sandwich panel was subservient to the lateral reinforcements from a mechanical standpoint. Thus, the height of the intermediate compartments was diminished. These sites were selected at locations where changes in geometric variables do not influence any coordinates. This eliminated the direct impact of changes in design variables on the results. Requesting local results from points whose coordinates change as geometric variables change would be misleading. For each set of variable values, we captured data from the same points (P1, P2, and P3), but these points have distinct coordinates, i.e., they are in a different zone of the model. This article makes use of the characteristics for typical steel: E = 210 GPA, 7890 kg/m³, and 0.29 [-] Poisson coefficient. The applied load intensity was N, the element type was SHELL63, and the average lattice element size was 2.5 mm. For the model’s sensitivity analysis, three design variables characterizing the most important stiffeners properties were chosen, Figure 2 shows the geometric variables LG1, LG2 and LG3 on Beam 1—Pattern 1. LG1 is the distance from the center of the beam to the inner wall of the beam in the direction of the section width; LG2 is the distance from the center of the section of the beam to the inner wall of the beam in the direction of the section height and LG3 is the thickness of all the walls of the beam.

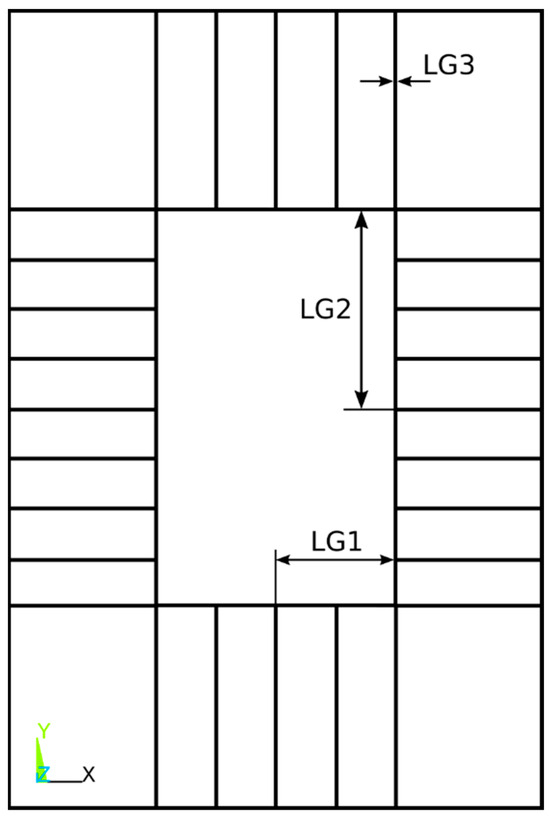
Figure 2. Geometric variables of the FEM model used in the sensitivity analysis [1].

The outer section dimensions are maintained. It is assumed, from an industrial standpoint, that all beams are constructed with panels of identical thickness. The goal is to obtain a set of reinforcements that is straightforward to assemble on a large scale.

3. Results and Discussion

3.1. Mesh Convergence

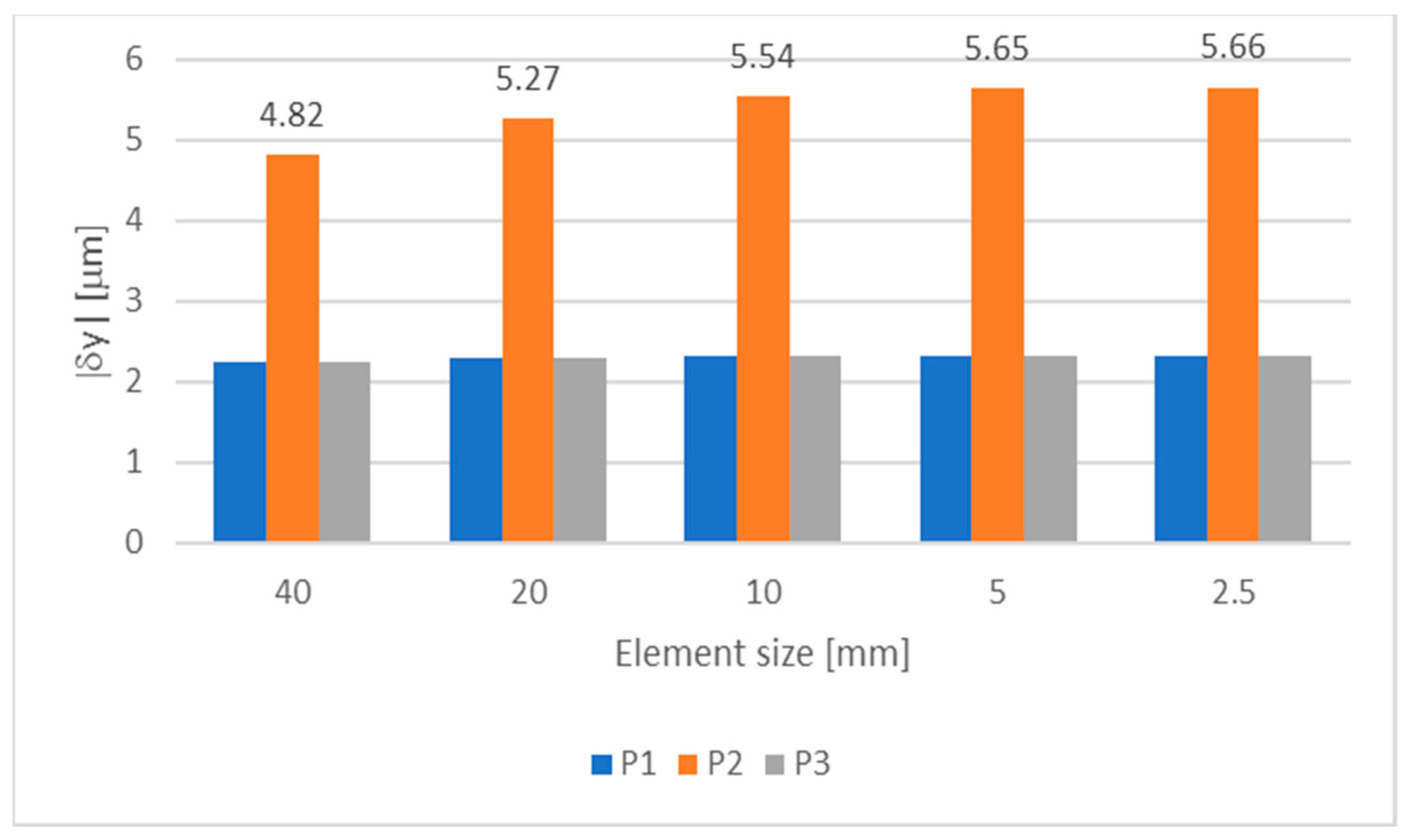
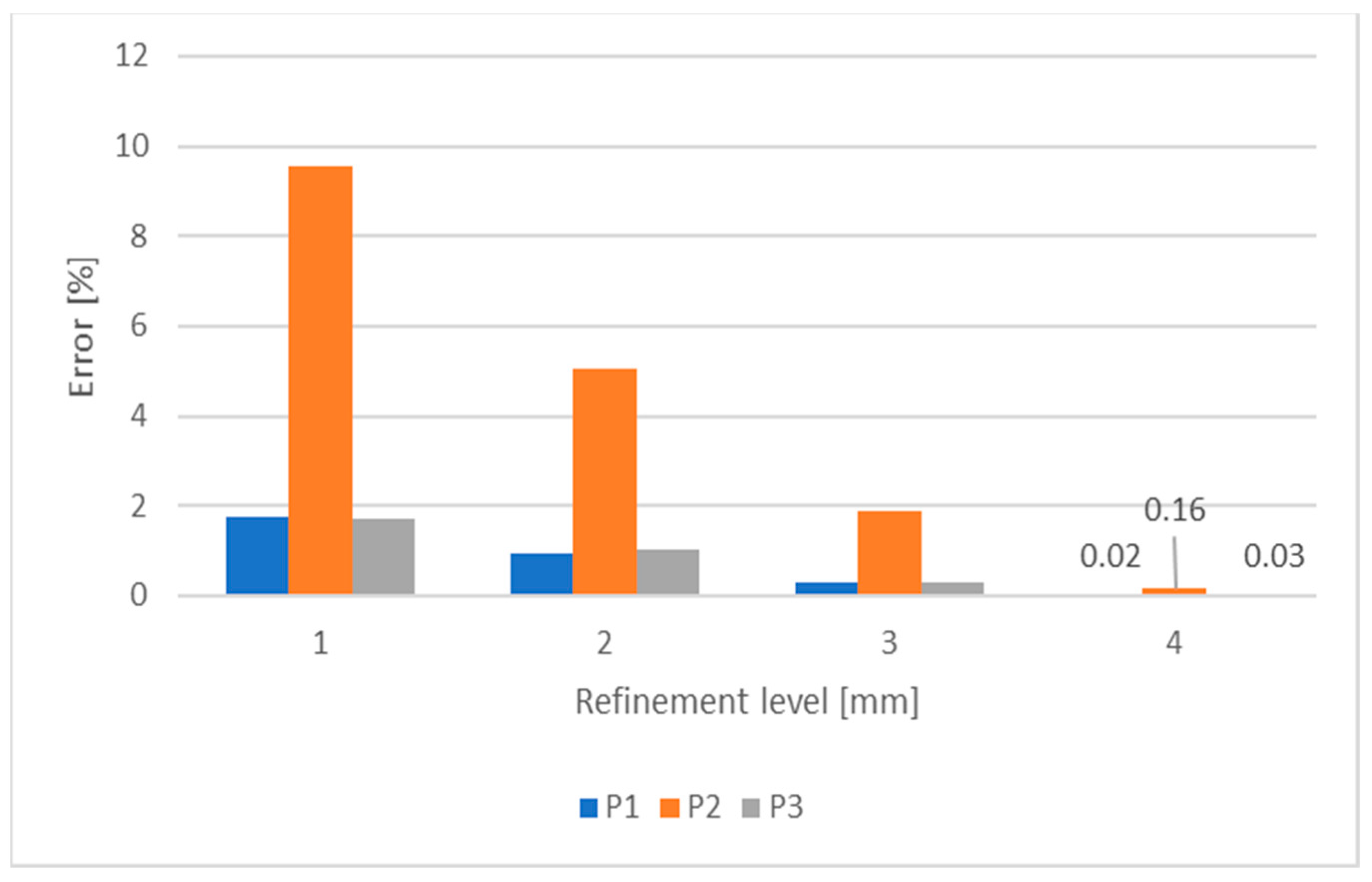
In order to obtain accurate results, a mesh sensitivity analysis was performed in ANSYS Mechanical APDL. Element sizes of 2.5, 5, 10, 20 and 40 mm were used. Four refinement levels were defined in order to compare the results of a mesh size with the ones with double element size. The y deflection was measured in points P1, P2 and P3, shown in Figure 1 (right). The results of the mesh convergence analysis are shown in Figure 3 and Figure 4.

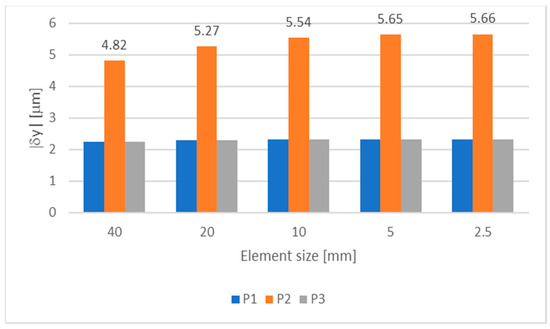
Figure 3. Mesh convergence analysis of the FEM model used in the sensitivity analysis: deflections.

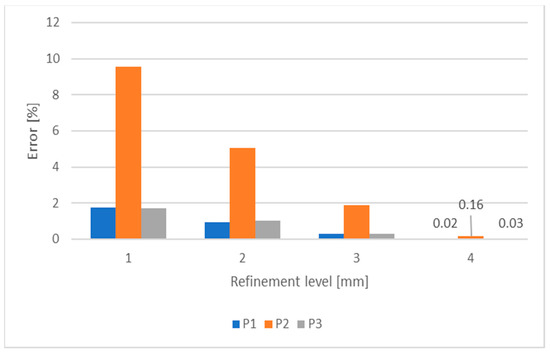
Figure 4. Mesh convergence analysis of the FEM model used in the sensitivity analysis: errors obtained.

As expected, mesh refinement increases the accuracy of results, as they vary less with decreasing element size. The element size of 2.5 mm was selected, as it originates accurate results, with a maximum error of 0.16%. In Figure 3 and Figure 4, the results are very close in every case, because the same model was used, with the same conditions. The only difference is the mesh size which is not a critical parameter here.

3.2. Sensitivity Analysis

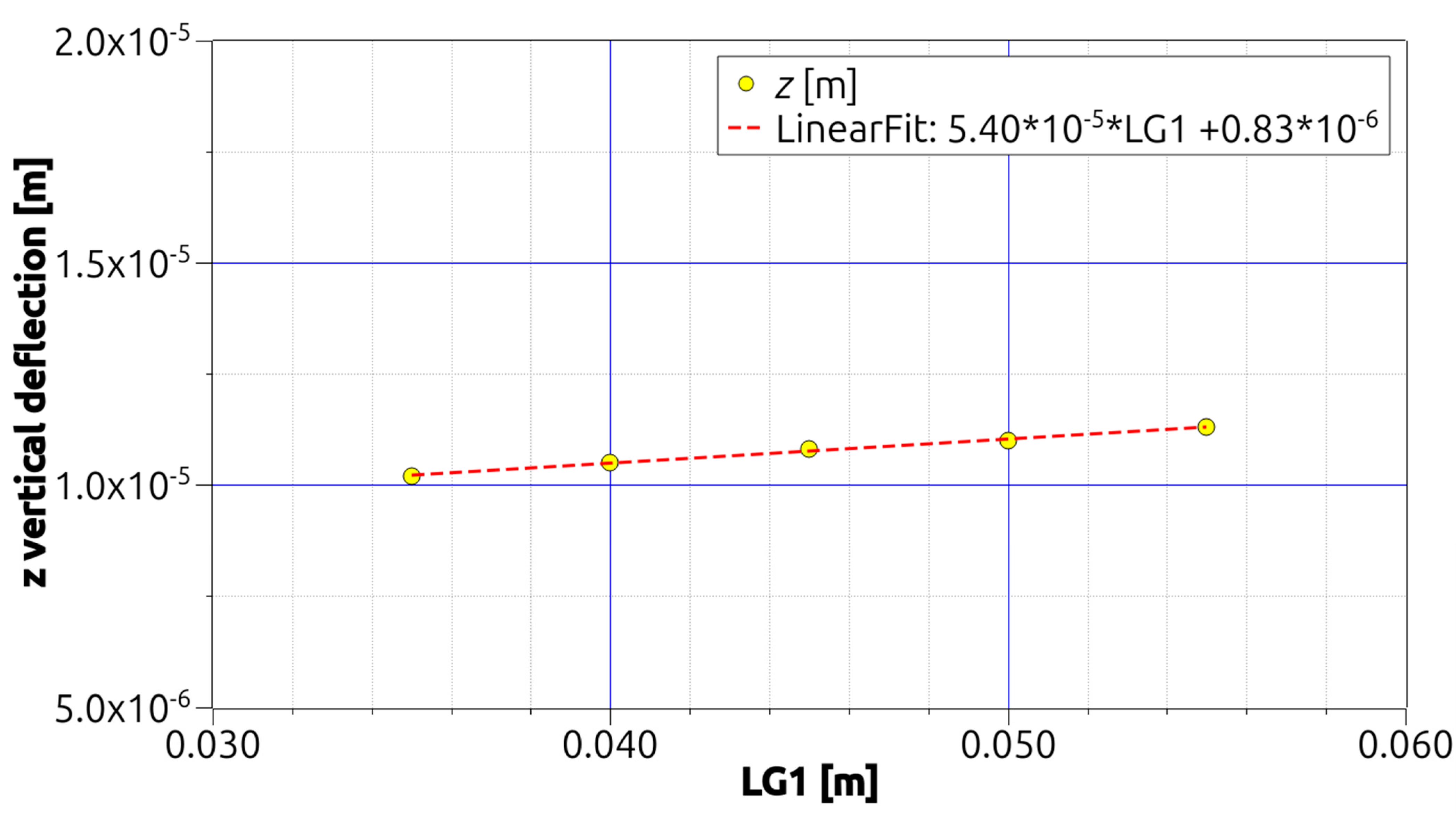
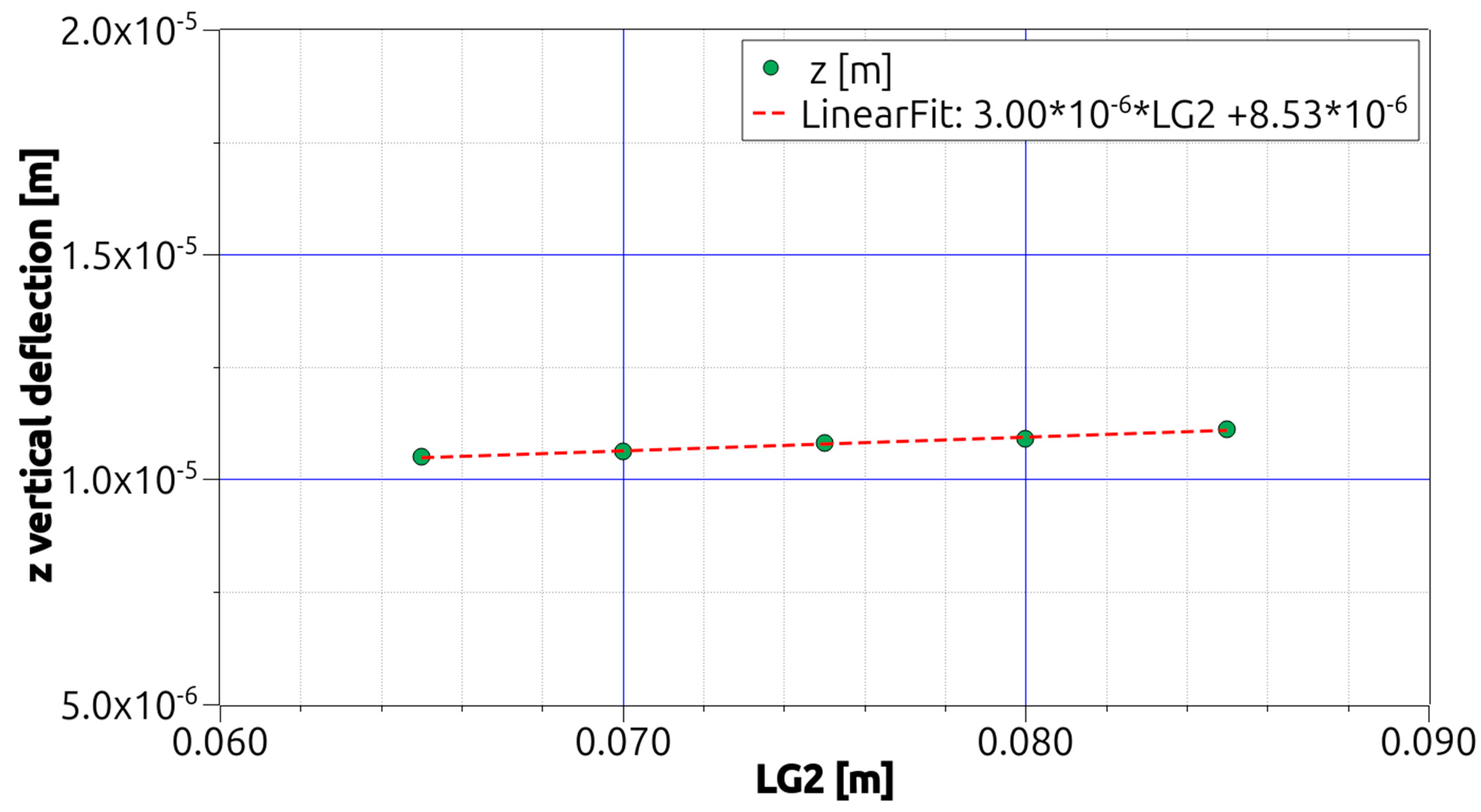
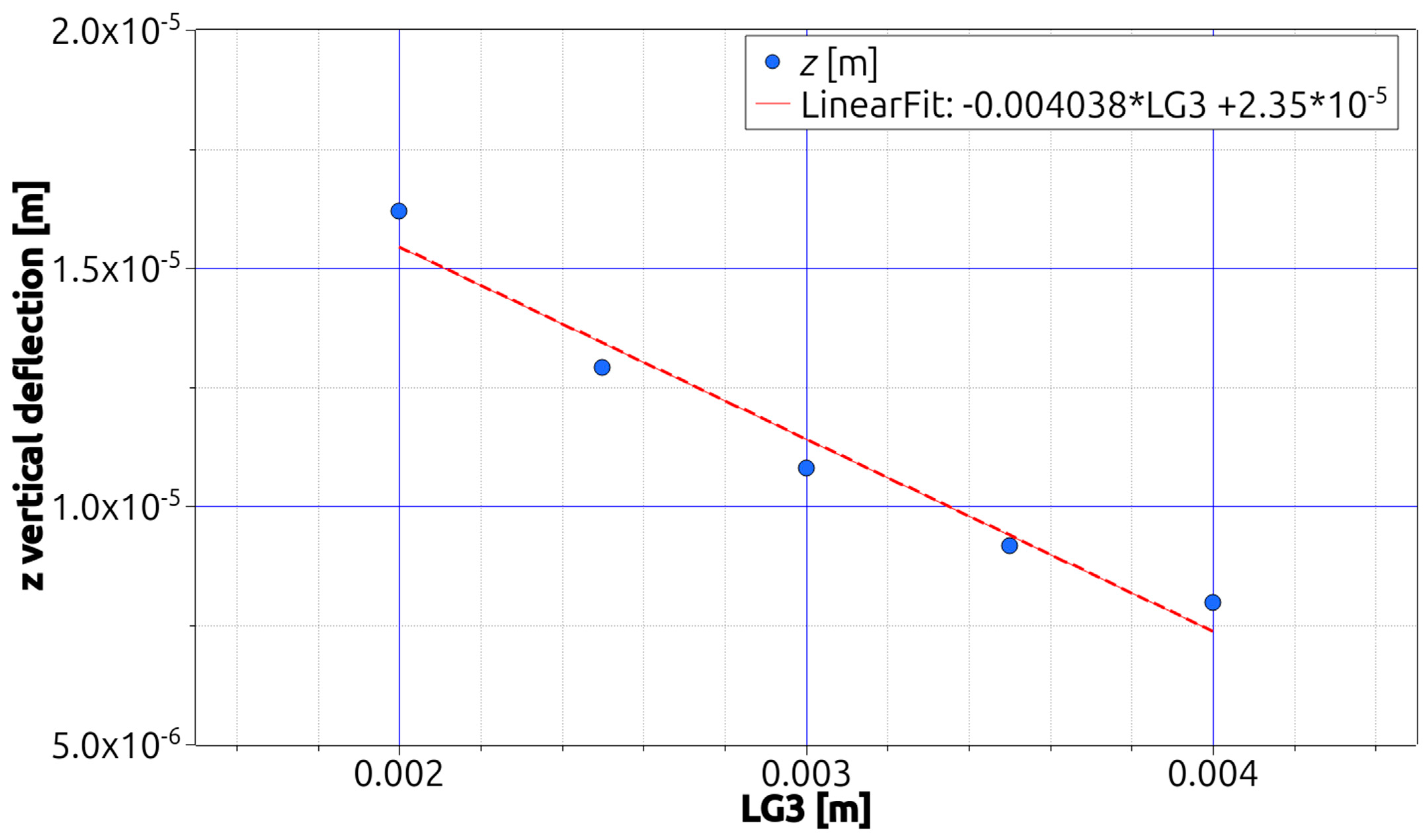
This section contains graphs generated from Table 1, Table 2 and Table 3. ANSYS MECHANICAL APDL was used to generate Table 1, Table 2 and Table 3 by modifying one variable at a time and repeatedly executing the ANSYS input file. Other variables are held constant in geometry. Nonetheless, the beam’s mass varies when a single geometric variable is altered. The linearity of the relationship between the variables and the deflections and between the variables and the mass was determined using a linear fit. Numerical and statistical information was displayed in Figure 5, Figure 6 and Figure 7 and Table 1, Table 2 and Table 3. Because the figures depict the total deflection of the three selected points in relation to the variable’s values and approximate trendlines, this was the case. In contrast, Table 1, Table 2 and Table 3 illustrate the masses and deflections of the obtained beams at each of the locations P1, P2, and P3. Figure 5, Figure 6 and Figure 7 are the graphical representation of the results shown in Table 1, Table 2 and Table 3. As the obtained results appear to show almost linear dependence on the parameters chosen, linear fits are added to the charts. The results are expressed as a single series, representing the aggregate of the absolute deflections at locations P1, P2, and P3 (see Figure 5, Figure 6 and Figure 7), for LG1, LG2, and LG3, respectively.

Table 1. Sensitivity analysis for the LG1 variable under bending loads.

j = 5	j = 4	j = 3	j = 2	j = 1
0.055	0.05	0.045	0.04	0.035	LG1
77.981	79.176	80.372	81.567	82.762	mass (kg)
−2.29 × 10−6	−2.18 × 10−6	−2.06 × 10−6	−1.95 × 10−6	−1.84 × 10−6	δyP1 (m)
−6.71 × 10−6	−6.67 × 10−6	−6.63 × 10−6	−6.58 × 10−6	−6.52 × 10−6	δyP2 (m)
−2.29 × 10−6	−2.18 × 10−6	−2.06 × 10−6	−1.95 × 10−6	−1.84 × 10−6	δyP3 (m)
1.13 × 10−5	1.10 × 10−5	1.08 × 10−5	1.05 × 10−5	1.02 × 10−5	δsum (m)

Table 2. Sensitivity analysis for the LG2 variable under bending loads.

j = 5	j = 4	j = 3	j = 2	j = 1
0.085	0.08	0.075	0.07	0.065	LG2
78.397	79.384	80.372	81.359	82.346	mass (kg)
−2.10 × 10−6	−2.08 × 10−6	−2.06 × 10−6	−2.04 × 10−6	−2.02 × 10−6	δyP1 (m)
−6.90 × 10−6	−6.75 × 10−6	−6.63 × 10−6	−6.51 × 10−6	−6.41 × 10−6	δyP2 (m)
−2.10 × 10−6	−2.08 × 10−6	−2.06 × 10−6	−2.04 × 10−6	−2.02 × 10−6	δyP3 (m)
1.11 × 10−5	1.09 × 10−5	1.08 × 10−5	1.06 × 10−5	1.05 × 10−5	δsum (m)

Table 3. Sensitivity analysis for the LG3 variable under bending loads.

j = 5	j = 4	j = 3	j = 2	j = 1
0.004	0.0035	0.003	0.0025	0.002	LG3
107.162	93.767	80.372	66.976	53.581	mass (kg)
−1.65 × 10−6	−1.84 × 10−6	−2.06 × 10−6	−2.34 × 10−6	−2.67 × 10−6	δyP1 (m)
−4.66 × 10−6	−5.49 × 10−6	−6.63 × 10−6	−8.27 × 10−6	−1.08 × 10−5	δyP2 (m)
−1.65 × 10−6	−1.84 × 10−6	−2.06 × 10−6	−2.34 × 10−6	−2.67 × 10−6	δyP3 (m)
7.97 × 10−6	9.17 × 10−6	1.08 × 10−5	1.29 × 10−5	1.62 × 10−5	δsum (m)

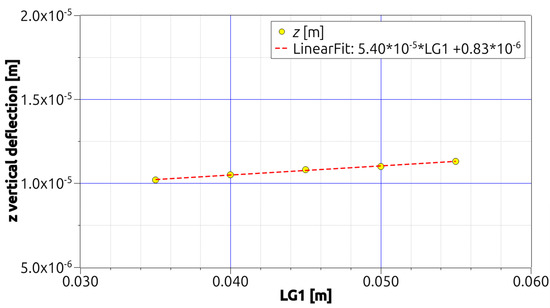
Figure 5. Variation of the z deflections with the LG1 variable under bending [1].

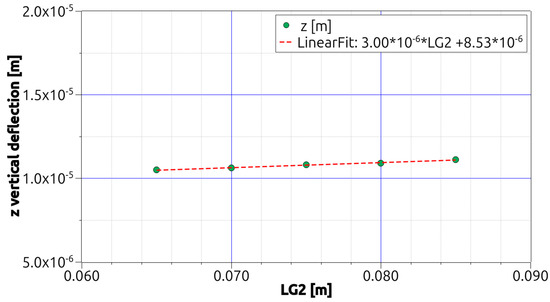
Figure 6. Variation of the z deflections with the LG2 variable under bending [1].

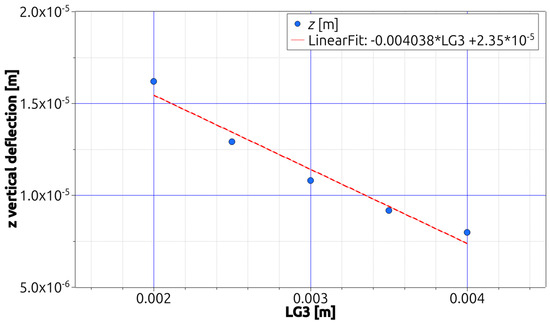
Figure 7. Variation of the z deflections with the LG3 variable under bending [1].

The deflection increases strictly as the LG1 (Figure 5) and LG2 (Figure 6) variables increase but decreases as the LG3 variable increases, see Figure 7. It can be seen that the results at points P1 and P3 are identical, as can be seen in Table 1, Table 2 and Table 3. In terms of the stiffness sensitivity of the investigated structure, variable LG3 is the most influential to its value as with doubling its value the vertical displacement reduces by half. In other cases, any increase of the parameter LG1 or LG2 lowers the resulting stiffness value −67% LG1 increase gives −10% stiffness decreases and 30% increase of LG2 results in −6.7% decrease, respectively. This is expected, as this variable is applied to all the walls of the beam, so its influence is total, while the influence of LG1 and LG2 on the mechanical behavior of the beam is partial, as it can be seen in Figure 5, Figure 6 and Figure 7. is possible to observe that the beams’ deflections are in the micrometer range, which, for applied load intensities of 1500 N in three-point bending and taking into consideration the beams’ thinness, indicates the beams’ excellent stiffness.

4. Conclusions

In result of performed analysis, it is clear that all the selected geometric variables, LG1, LG2, and LG3, are adequate for optimization objectives. The results suggest that the FEM model’s deflections are sensitive to them. Initial variable values were specified in order to enable a large search space. The models are constrained geometrically, primarily in terms of their inner section. The values of variables LG1 and LG2 cannot be so low as to cause structural elements from the sides or top/bottom to collide, preventing further optimization evaluations. This precludes the discovery of an optimal solution. Otherwise, the interior ribs will be smaller than the average element size, leading to defects. LG3 is the least essential variable in this regard. Nevertheless, it must be high enough to prevent substantial nonlinear effects in future practical applications, while remaining low enough to permit the production of lightweight components suitable for the applications intended by this work. It has been shown that parameterizing the ANSYS input file is an effective way to determine the system’s sensitivity to the investigated design variables. The results of the sensitivity analysis may be used in the future to determine the variable weights for optimization techniques and processes. This study presents only the analysis for a single beam. Therefore, generalization of the findings for similar beams with slightly different geometries is, therefore, not possible. The limitations of the methodology are, therefore, not being unable to obtain a generalized model that allows the prediction of the sensitivity of the studied variables for similar beams, with slightly different geometry. Nevertheless, the study proves that the three geometric variables are useful for design optimization purposes.