Procedure of Forming Power Law Functionally Graded Material (FGM) Plate Using ANSYS ^†

Abstract

The deflection, stress, and heat transfer of a plate made of functionally graded material (FGM) were investigated using the data of mechanical loads and temperatures using ANSYS Workbench. The 2D planar problem-solving method in ANSYS Workbench was used to simulate the FGM plate with the neutral surface for the mechanical problem. The problem of stable heat transfer for the plate was assumed for the solid block for the FGM plate. The results were compared with those of previous studies to validate the reliability of the newly fabricated FGM. The thin plate theory for materials with mechanical properties was considered with the power law distribution as each layer had identical thickness and temperature. Each layer showed material properties that changed with the thickness of the plate.

1. Introduction

Materials with improved durability, plasticity, high bearing capacity, and temperature resistance have been researched in structural mechanics. As one of such materials, functional graded materials (FGM) are studied widely to apply them to aviation, space, construction, and mechanical engineering. FGM is a composite material characterized by continuously changing mechanical properties. Such properties help overcome the limitations of traditional composite materials and improve the ability to withstand mechanical and thermal loads in the structure. To expand the application of FGM, the behavior of materials with various methods and models is required. Research on the mechanical properties of FGM has been conducted by many researchers. Thai and Choi analyzed the FGM plate for bending and free vibration using the first-order shear theory [1]. Singha et al. analyzed it subjected to uniformly distributed loads by the finite element method [2]. Olley analyzed the application of FGM in aircraft structures [3,4]. The result of the previous research was compared to that of this research to provide reference and basic information for constructing appropriate models to understand the properties of FGM plates with muli-layers.

2. Materials and Methods

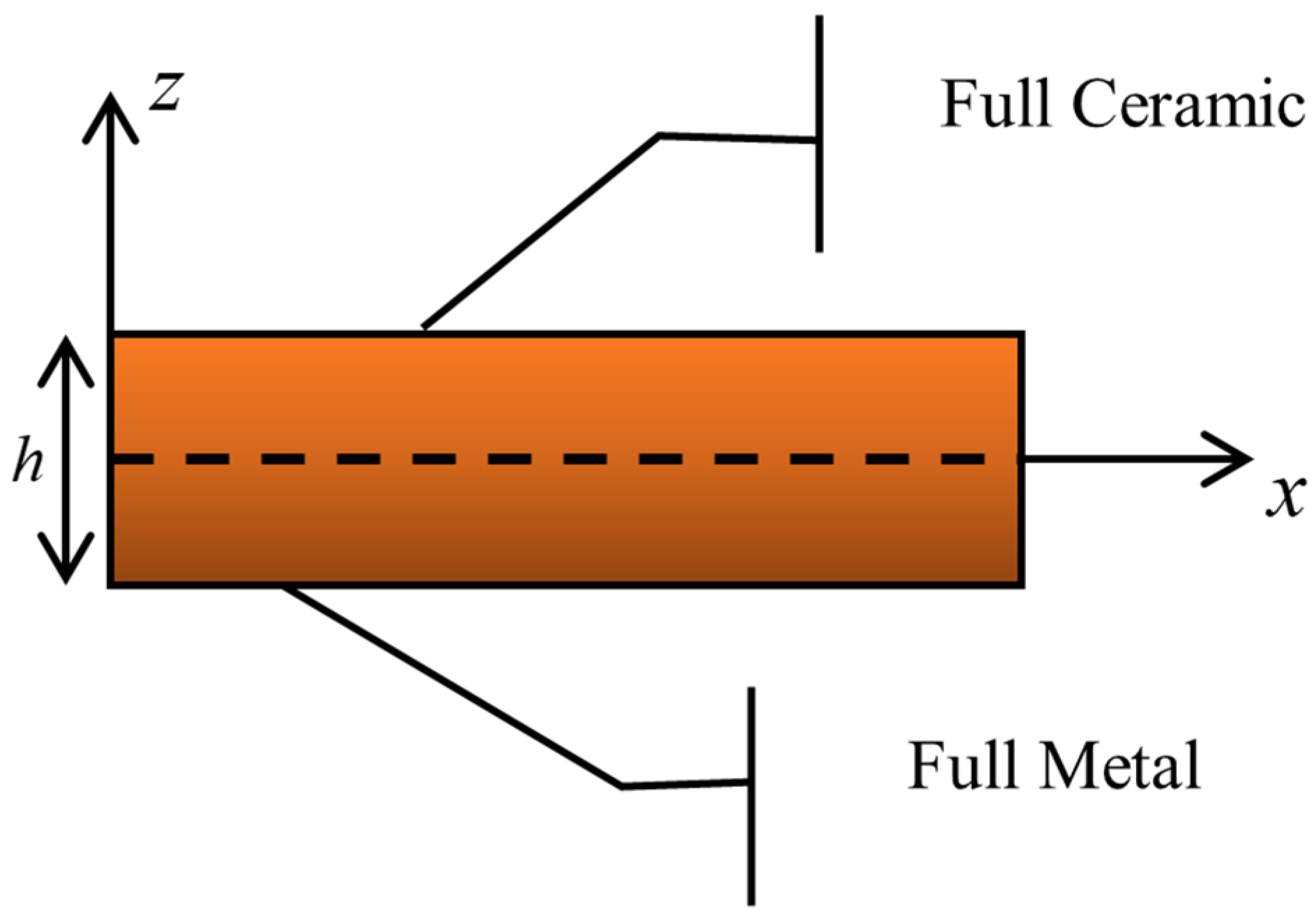
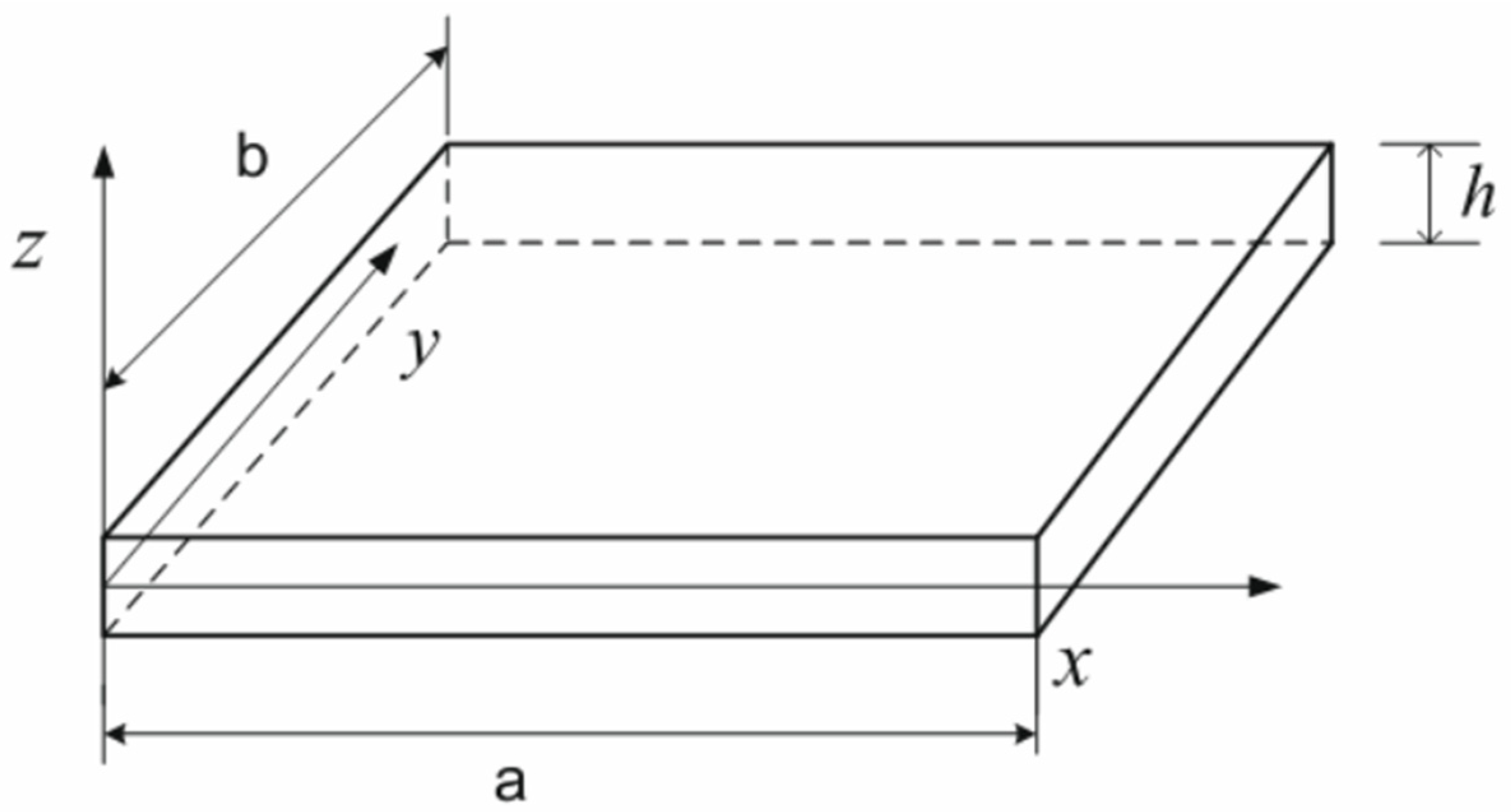
2.1. Structure of FGM

The ceramic and metal components are linearly distributed along the structural wall, which has either a ceramic-rich surface or a metal-rich surface in the FGM plate. The FGM plate with such properties is called a power law FGM plate (P-FGM). The structure of P-FGM is shown in Figure 1.

Material properties of P-FGM depend on the p-value and the position in the plate and vary according to a power law according to Equation (1).

$$\begin{array}{l}{V}_c(z)={\left(\frac{2z+h}{2h}\right)}^p, -\frac{h}{2}\le z\le \frac{h}{2}\\ V_m(z)=1-V_c(z)\end{array}$$

(1)

where p is a non-negative number called the volume fraction index, h is the thickness of the structure, and m and c indicate metal and ceramic components. According to the law of material distribution in Equation (1), when p = 0, the homogeneous plate is ceramic; when p ≥ 1, the proportion of ceramic in the P-FGM plate decreases.

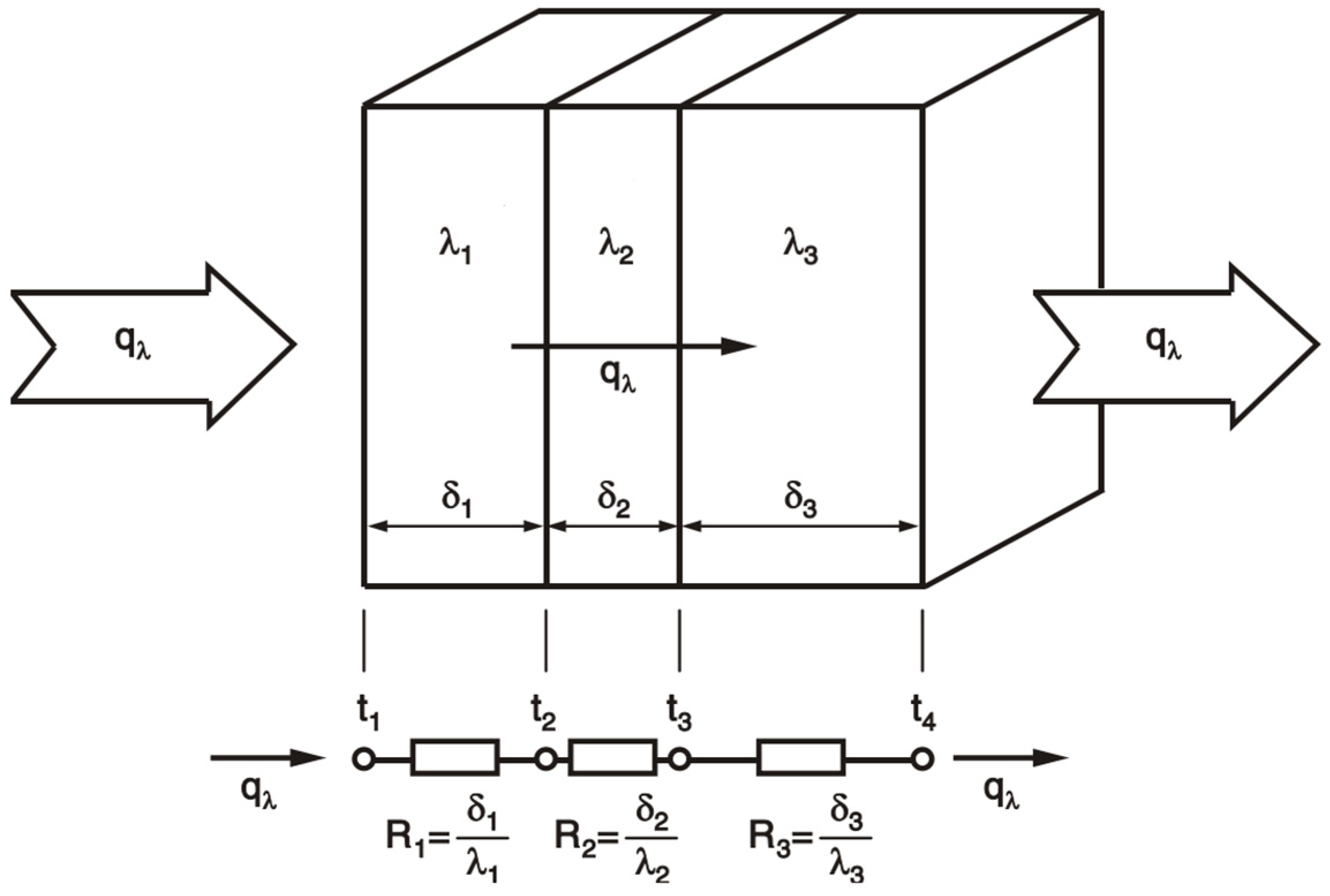
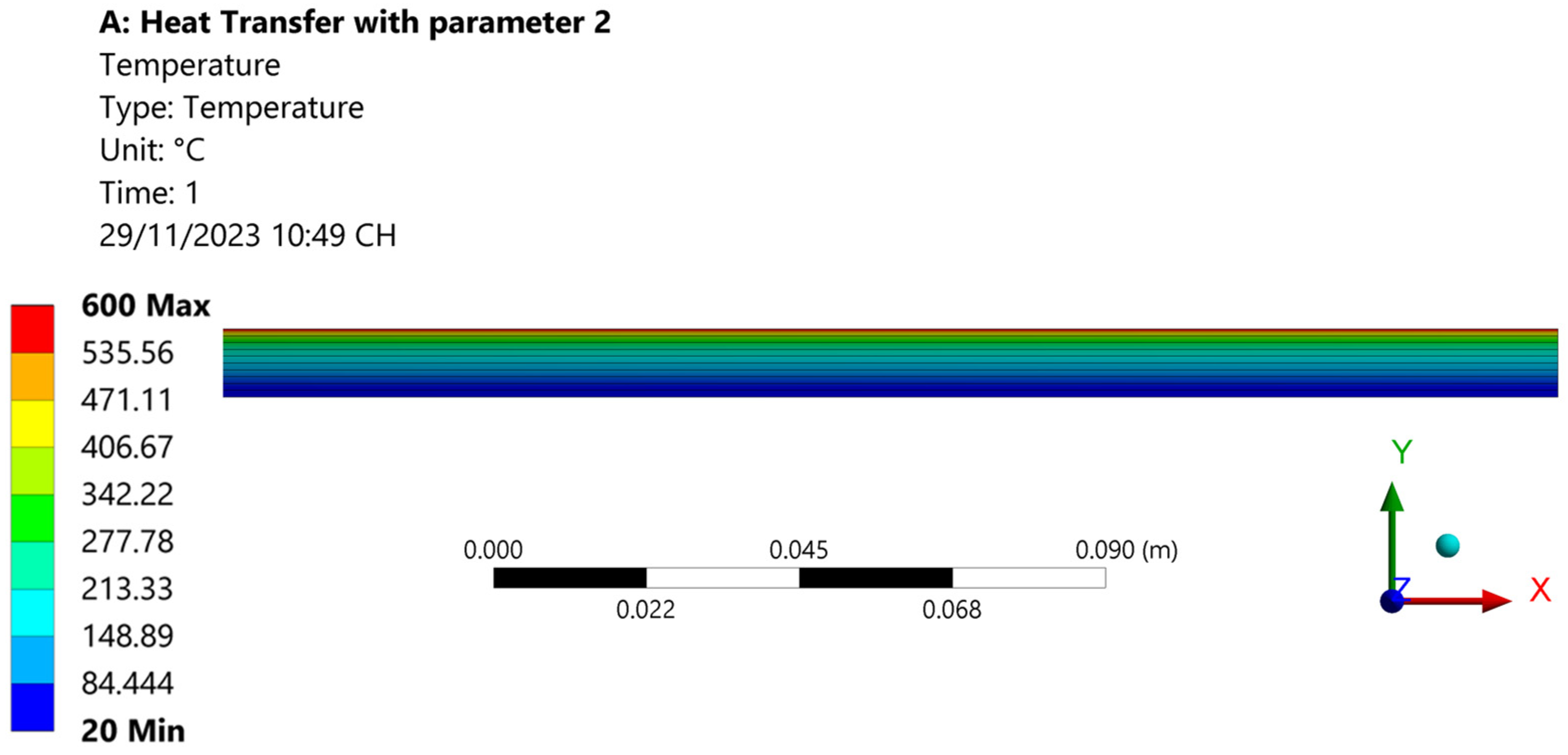
2.2. Heat Transfer in P-FGM

Assuming that a P-FGM plate has three layers with each layer’s thickness of δ₁, δ₂, and δ₃ (m) and the thermal conductivity of λ₁, λ₂, and λ₃ (W/m∙temp), and the surface temperatures are ($t_1$ − $t_4$), Figure 2 shows the layers affected by the temperature of the P-FGM plate.

Then, heat flux through the layers is calculated using Equation (2).

$$\left.\begin{array}{l}q=\frac{{\lambda }_1}{{\delta }_1}(t_1-t_2)\\ q=\frac{{\lambda }_2}{{\delta }_2}(t_2-t_3)\\ q=\frac{{\lambda }_3}{{\delta }_3}(t_3-t_4)\end{array}\right\}$$

(2)

From Equation (2), the following relationship is defined.

$$\left.\begin{array}{l}{t}_1-t_2=q\frac{{\delta }_1}{{\lambda }_1}\\ t_2-t_3=q\frac{{\delta }_2}{{\lambda }_2}\\ t_3-t_4=q\frac{{\delta }_3}{{\lambda }_3}\end{array}\right\}$$

(3)

($t_1$ − $t_4$) is calculated using Equation (4), and the heat flux is estimated using Equation (5).

$$\left(t_1-t_4\right)=q\left(\frac{{\delta }_1}{{\lambda }_1}+\frac{{\delta }_2}{{\lambda }_2}+\frac{{\delta }_3}{{\lambda }_3}\right)$$

(4)

$$q=\frac{t_1-t_4}{\frac{{\delta }_1}{{\lambda }_1}+\frac{{\delta }_2}{{\lambda }_2}+\frac{{\delta }_3}{{\lambda }_3}}=\frac{t_1-t_4}{R_{{\lambda }_1}+R_{{\lambda }_2}+R_{{\lambda }_3}}$$

(5)

For the plate with n layers, the heat flux is estimated using Equation (6).

$$q=\frac{t_1-t_{(n+1)}}{{\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{{\lambda }_i}}}=\frac{t_1-t_{(n+1)}}{{\displaystyle \sum _{i=1}^n{R}_i}}{(\mathrm{W}/\mathrm{m}}^2)$$

(6)

where ${\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{{\lambda }_i}}$ is the thermal conductivity of a layer of the plate.

The heat flux of the contact layer of the plate is defined as

$$q=\frac{t_1-t_{(n+1)}}{{\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{{\lambda }_i}}}=\frac{t_1-t_{(n+1)}}{{\displaystyle \sum _{i=1}^n{R}_i}}(W/m^2)$$

(7)

Therefore, the temperature of the layer is calculated as

$$t_{(k+1)}=t_1-q{\displaystyle \sum _{i=1}^k\frac{{\delta }_i}{{\lambda }_i}}$$

(8)

3. Results

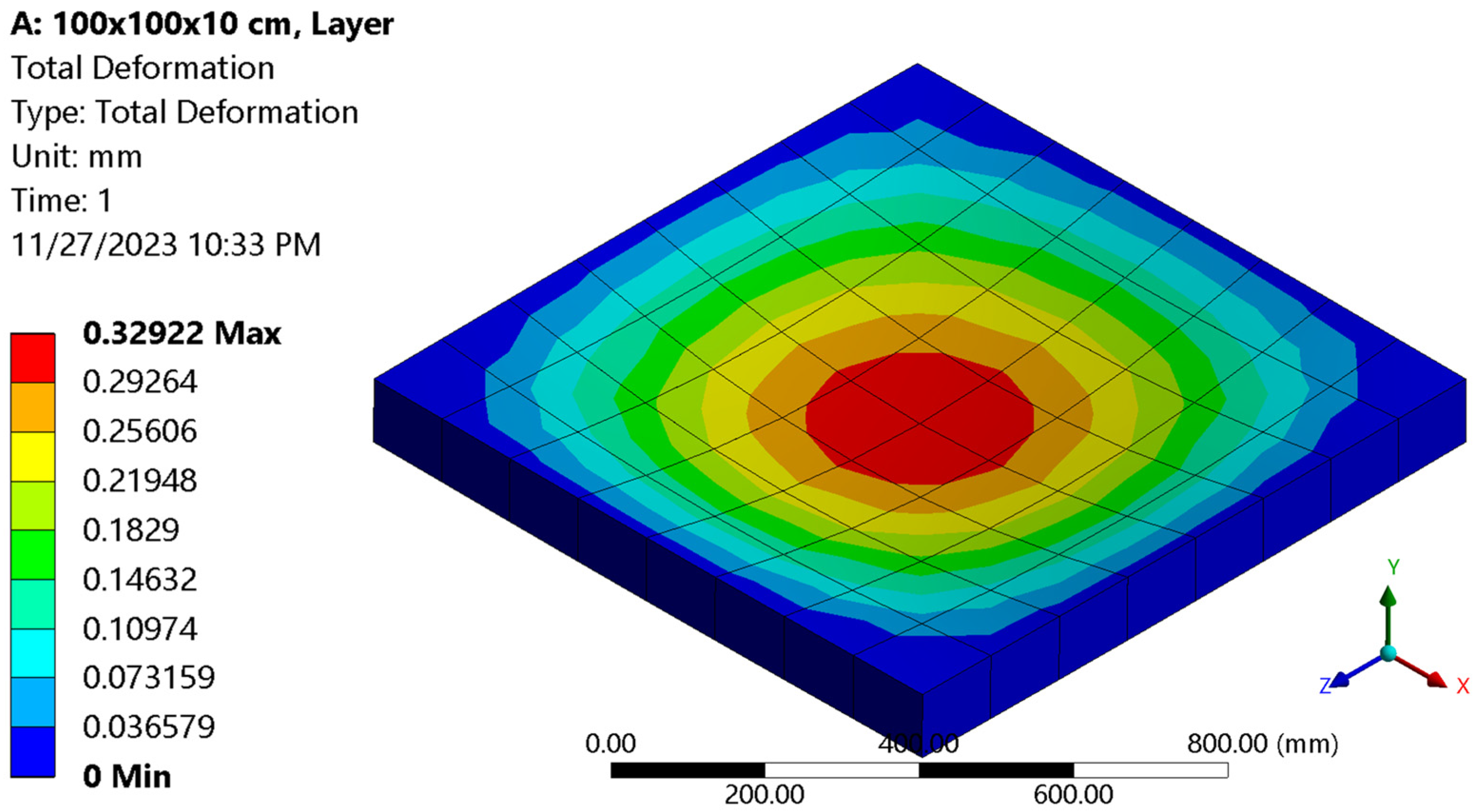
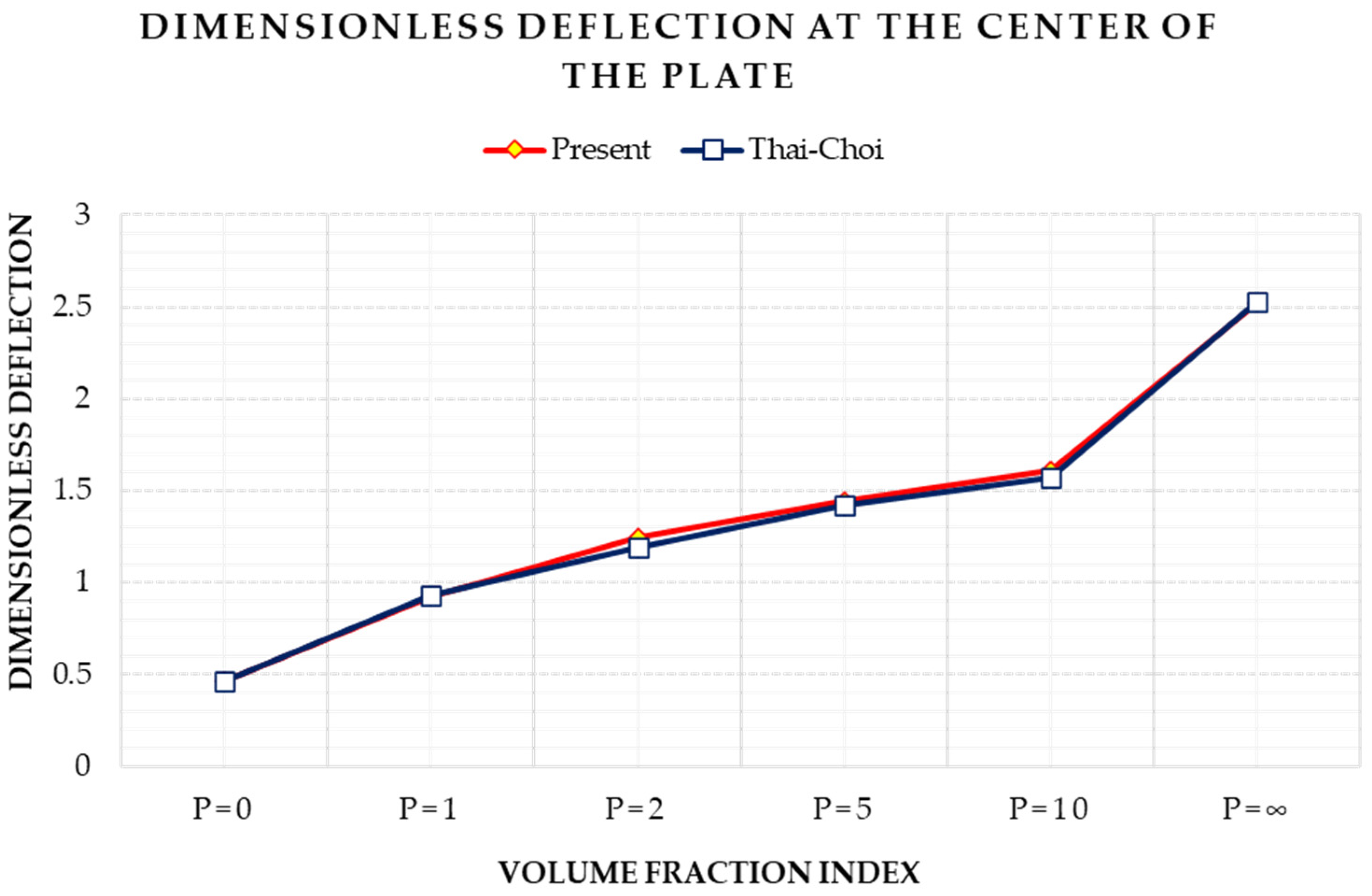
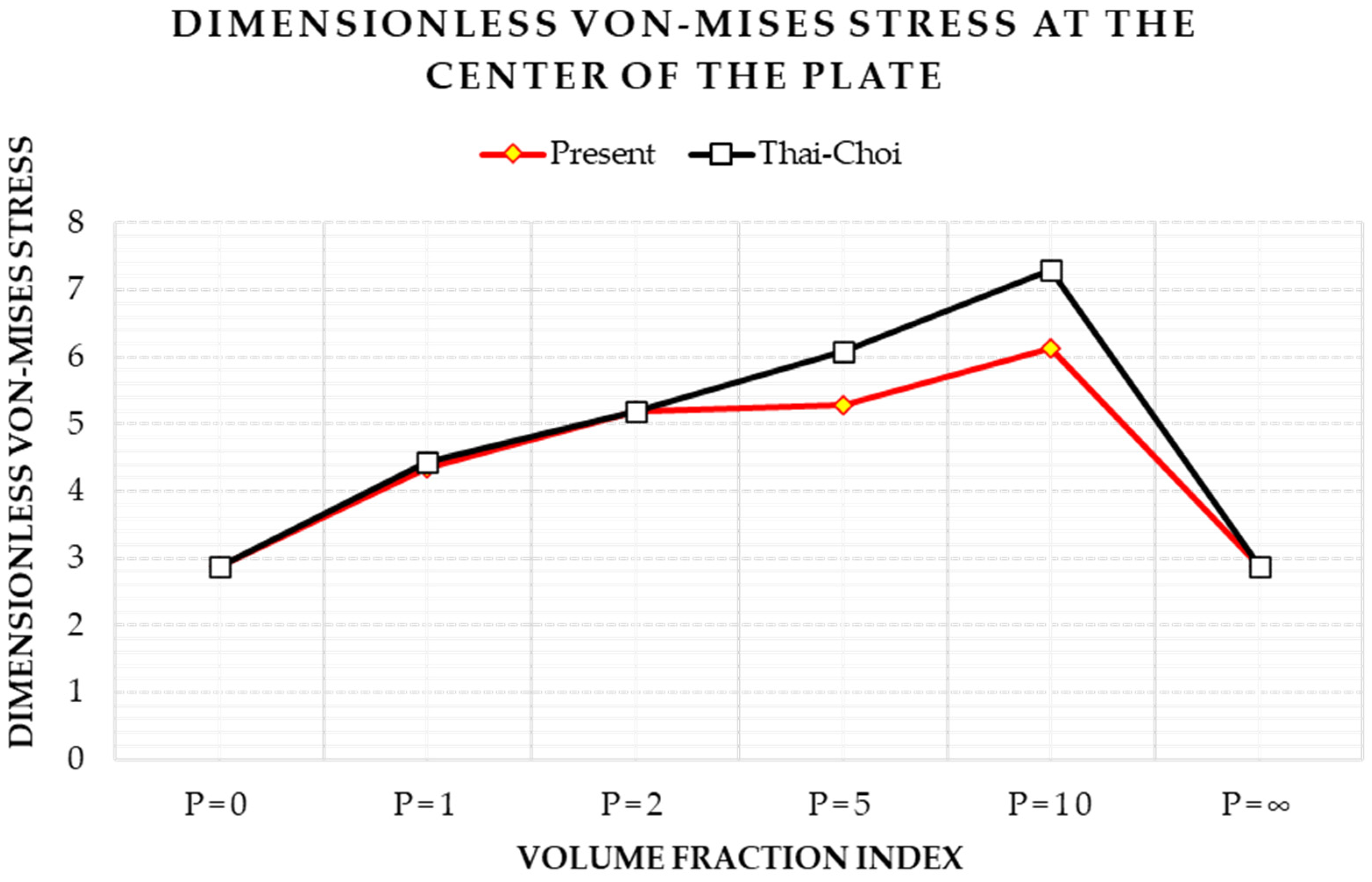
3.1. P-FGM Plate with Uniformly Distributed Load

For different FGM plates, bending under uniform load ($q_0=1 \mathrm{MPa}$), and the responses of simple support with the SSSS boundary condition were estimated. The material properties of the plate are shown in

Table 1. Material properties of P-FGM plate.

Material Properties	Metal Aluminum (Al)	Ceramic Alumina (Al2O3)
E (GPa)	70	380
ν	0.3	0.3

. Numerical results are compared with those of previous studies to show the reliability of the proposed P-FGM model. Figure 3 shows the P-FGM plate with its dimensions.

For an elastic square plate with a surface on the x-y plane and a thickness in the z-direction, tensile (compression) modulus E is defined as a function of E = E(z), and Poisson’s ratio ν for smooth variation in thickness with a given rule is defined as a function of ν = ν(z). The square plate has a dimension of a × b × h = 100 × 100 × 10 or a/h = 10. As P-FGM has continuously varying mechanical properties, it was assumed that each layer of the P-FGM plate has different material parameters to model the plate in ANSYS Workbench. Using the power-law distribution, the details of 10 layers of the FGM plate were determined, as shown in

Table 2. Layer’s material properties of the P-FGM plate.

$\frac{\mathit{z}}{\mathit{h}}$	Young’s Modulus (Pa)
	p = 0	p = 1	p = 2	p = 5	p = 10	p = ∞
0.45	3.80 × 1011	3.65 × 1011	3.50 × 1011	3.10 × 1011	2.56 × 1011	7.00 × 1010
0.35	3.80 × 1011	3.34 × 1011	2.94 × 1011	2.08 × 1011	1.31 × 1011	7.00 × 1010
0.25	3.80 × 1011	3.03 × 1011	2.44 × 1011	1.44 × 1011	8.75 × 1010	7.00 × 1010
0.15	3.80 × 1011	2.72 × 1011	2.01 × 1011	1.06 × 1011	7.42 × 1010	7.00 × 1010
0.05	3.80 × 1011	2.41 × 1011	1.64 × 1011	8.56 × 1010	7.08 × 1010	7.00 × 1010
−0.05	3.80 × 1011	2.10 × 1011	1.33 × 1011	7.57 × 1010	7.01 × 1010	7.00 × 1010
−0.15	3.80 × 1011	1.79 × 1011	1.08 × 1011	7.16 × 1010	7.00 × 1010	7.00 × 1010
−0.25	3.80 × 1011	1.48 × 1011	8.94 × 1010	7.03 × 1010	7.00 × 1010	7.00 × 1010
−0.35	3.80 × 1011	1.17 × 1011	7.70 × 1010	7.00 × 1010	7.00 × 1010	7.00 × 1010
−0.45	3.80 × 1011	8.55 × 1010	7.08 × 1010	7.00 × 1010	7.00 × 1010	7.00 × 1010

.

For the material properties with p = 2 and load with the SSSS boundary condition, the deflection and the von Mises stress of the P-FGM plate under a uniform load are shown in Figure 4 and Figure 5.

The non-dimensional result of the modeled P-FGM was similar to that of Ref. [1]. The following equations were used to convert numerical results to non-dimensional ones in ANSYS Workbench [1].

Non-dimensional deflection of FG plate under uniform load was defined as

$${\overline{w}}_{\max }=\frac{10h^3{E}_c}{p_0{b}^4}w\left(\frac{a}{2};\frac{b}{2}\right)$$

(9)

where $w\left(\frac{a}{2};\frac{b}{2}\right)$ is deflection in the center of the plate.

The non-dimensional von Mises stress of the P-FGM plate under uniform load was calculated as

$${\overline{\sigma }}_{xx}(z)=\frac{h}{q_{0}a}{\sigma }_x\left(\frac{a}{2},\frac{b}{2},z\right)$$

(10)

where ${\sigma }_x\left(\frac{a}{2},\frac{b}{2},z\right)$ is von Mises stress in the center of the plate.

For the P-FGM plate with 10 layers, the result of the modeled plate in this research and the other research was compared, as shown in

Table 3. Non-dimensional result of P-FGM plate with 10 layers.

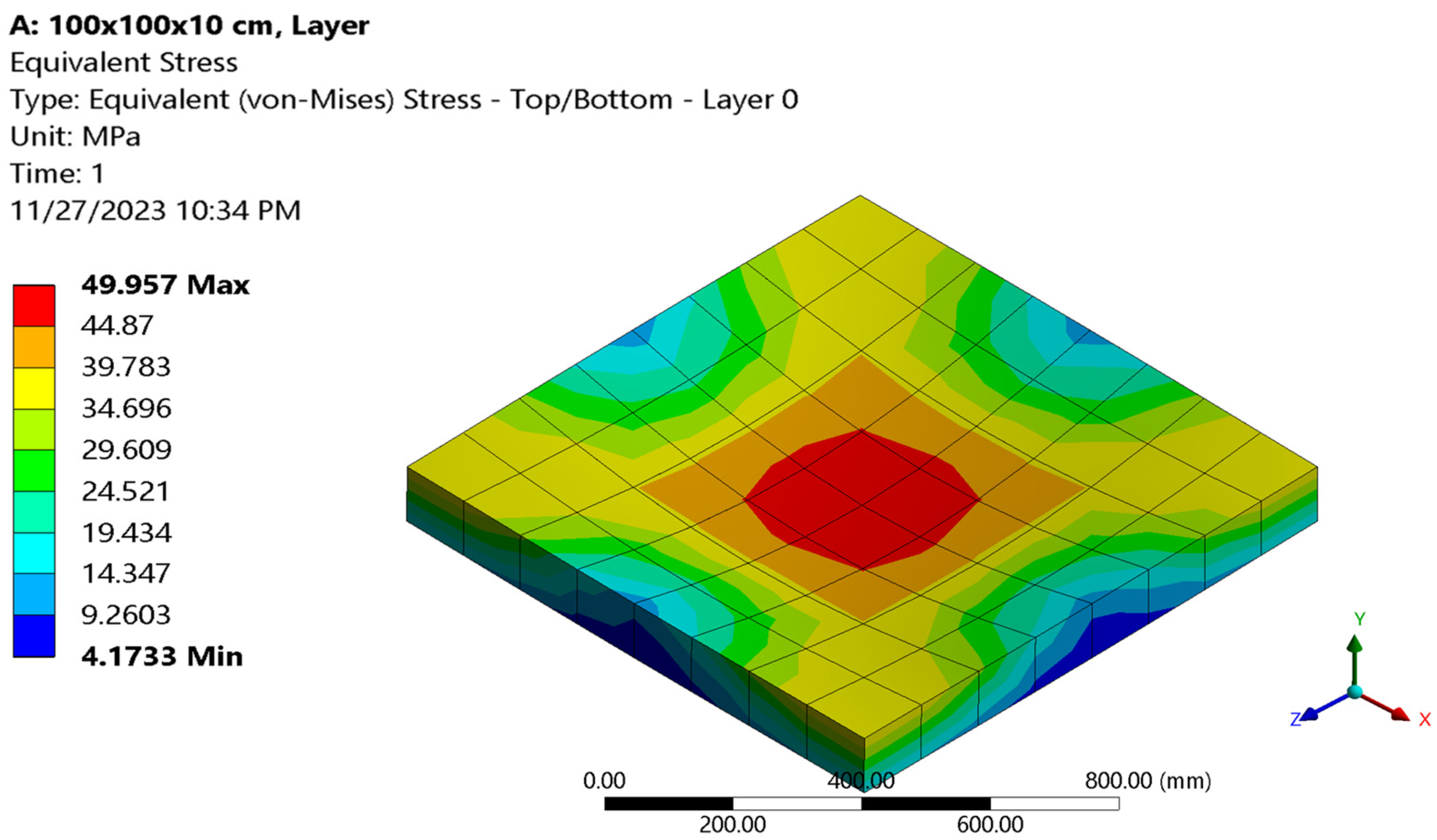
p	Reference	$\mathit{w}$max (mm)	$\mathit{w}$max (Non-Dimensional)	σmax (MPa)	σmax (Non-Dimensional)
2	This research	0.32922	1.251	49.957	4.9957
	[1]		1.1909		5.1852
	Error		4.8%		4%

.

For the P-FGM plate with 20 layers, the result of the modeled plate in this research and the other research was compared, as shown in

Table 4. Non-dimensional result of P-FGM plate with 20 layers.

p	Reference	$\mathit{w}$max (mm)	$\mathit{w}$max (Non-Dimensional)	σmax (MPa)	σmax (Non-Dimensional)
2	This research	0.32858	1.2486	51.859	5.1859
	[1]		1.1909		5.1852
	Error		4.6%		4%

.

Remodeling the FG plate with 40 layers, the result of the modeled plate in this research and the other research was compared, as shown in

Table 5. Non-dimensional result of FGM plate with 40 layers.

p	Reference	$\mathit{w}$max (mm)	$\mathit{w}$max (Non-Dimensional)	σmax (MPa)	σmax (Non-Dimensional)
2	This research	0.32858	1.2486	51.859	5.1859
	[1]		1.1909		5.1852
	Error		4.6%		4%

.

The results of dimensionless deflection and von Mises stress in different volume ratios were compared in Figure 6 and Figure 7.

3.2. Influence of Temperature

Assuming the elastic square plate of size 200 × 200 × 10 (mm), the square plate of P-FGM had a ceramic-rich top surface and metal-rich bottom surface, material parameters changed linearly according to the P-FGM model, and volume fraction index p = 2, it was found that the P-FGM plate was affected by temperature. The ceramic-rich surface endured heat up to 600 °C, and the metal-rich surface only afforded heat up to 20 °C. Details of the properties of ceramic and metal surfaces of the square plate are presented in

Table 6. Properties of ceramic and metal surfaces of P-FGM plate.

Material Properties	Metal Aluminum (Al)	Ceramic Alumina (Al2O3)
E (GPa)	70	380
ν	0.3	0.3
ρ (kg/m3)	2.707	3
Thermal Conductivity k (W/mK)	204	2.09

.

In this research, a steady heat transfer from one surface of the plate to the other was considered. By dividing the plate into many small layers and using their material properties, a solid plate model with dimensions of 200 × 200 × 10 (mm) was constructed, as shown in Figure 8.

Table 7. Properties of 10 layers of P-FGM plate in 200 × 200 × 10 (mm).

$\frac{\mathit{z}}{\mathit{h}}$	Volume Faction Index (p = 2)
	E (MPa)	ρ (Kg/m3)	ν	K (W/mK)
0.45	1.47	2.985	0.3	12.19
0.35	1.39	2.956	0.3	32.38
0.25	1.31	2.927	0.3	52.57
0.15	1.23	2.897	0.3	72.76
0.05	1.15	2.868	0.3	92.95
−0.05	1.06	2.839	0.3	113.14
−0.15	9.84	2.810	0.3	133.33
−0.25	9.03	2.780	0.3	153.52
−0.35	8.22	2.751	0.3	173.71
−0.45	7.41	2.722	0.3	193.90

presents the details of 10 layers of the P-FGM plate of the size of 200 × 200 × 10 (mm).

Using the steady-state analysis in Ansys Workbench, the heat transfer of the plate was simulated, as shown in Figure 9.

The comparison of the results of the software simulation and the theory are shown in

Table 8. Comparison of heat transfer results simulated using software and calculated with theory.

$\frac{\mathit{z}}{\mathit{h}}$	Volume Faction Index (p = 2)
	T (°C) (Project)	T (°C) (Theory)	Error
0.45	600	600.00	0.00%
0.35	373.09	371.32	0.47%
0.25	287.63	285.64	0.69%
0.15	232.45	230.57	0.81%
0.05	190.26	188.61	0.87%
−0.05	155.09	153.77	0.85%
−0.15	124.20	123.24	0.77%
−0.25	96.031	95.46	0.60%
−0.35	69.60	69.44	0.23%
−0.45	44.21	44.47	0.59%

, which presents similar results for the two methods.

4. Conclusions

The mechanical behavior and heat transfer properties of the P-FGM plate were explored in this research. Specifically, a model was established according to the power-law distribution. The result showed the maximum deflection and stress at the center of the plate, as well as the heat transfer through the layers of the plate. A comparison of the results of other research proved the reliability of this research’s model. It was found that the modeled P-FGM plate helped understand the properties and heat transfer of the plate and provided intuitive results. However, the model needs improvement as it was constructed based on the properties of the P-FGM plate estimated using software. Thus, variables might not be optimized for the model. This produced simple numerical results, which were not enough to explain the various problems in the plate’s structure. The research method using ANSYS also needs to be improved for the construction of a better model.