Genetic Algorithm-Based Optimal Protection Scheme for the Coordination of Bi-Directional Overcurrent Relays in a Carbon-Free AC Microgrid ^†

Abstract

With the increasing predilection for renewable energy sources across the world, the novel idea of a miniature version of a grid, called a microgrid, has emerged. The efficiency and sustainability of a power grid increase by integrating distributed energy resources (DERs). However, designing an optimum protection scheme has become a substantial challenge due to bi-directional power flows and varying fault levels in the microgrid with distributed energy resources (DERs). The existing protection strategies are not capable of dealing with the different operational states and natures of DERs. Therefore, modifications to the conventional protection schemes are required to benefit from the advantages of de-centralized power generation. Optimum co-ordination between the protection devices (PDs) is needed to achieve fast, secure, and reliable protection of the system. This paper proposes a protection philosophy for a renewable-based AC microgrid and validates its resilience by analyzing the response of the system in different faulty scenarios. Moreover, a genetic algorithm (GA) is used to optimize the proposed protection scheme to achieve a cost-effective, resilient, reliable, and long-term solution for sustainable power generation.

1. Introduction

In today’s world, energy inadequacy has turned into a serious challenge that deserves our attention. As a result, the worldwide energy supply is being drained, and the conventional resources of power generation will one day be depleted. Over the past few years, the capacity of solar and wind has increased to 20% and 25% of the total generation alone [1]. These renewable sources are interconnected as distributed generation in the form of a microgrid, which improves the utilization efficiency of renewable energy compared to large-scale power grids.

As the microgrid contains de-centralized sources of generation, its protection and control are also a big challenge because it has to provide high reliability. Conventional protection settings cannot be used due to their robust nature, and hence, a well-coordinated protection system is required because the fault current in a grid-connected and islanded mode of operation of the microgrid is very different. Apart from this, due to distributed generation, in case of the occurrence of any fault, bi-directional power flow can also occur, which has to be considered while designing a protection scheme for a microgrid.

Taking into account the influence on fault currents of distribution generation (DG) and network locations, an ideal coordination scheme is created using an optimization approach called the genetic algorithm (GA). The optimum coordination approach intends to increase the sensitivity reliability of the protective system by reducing the working duration of overcurrent relays (OCRs) using a deviant tripping characteristic [2]. This paper has proposed a model of a carbon-free AC microgrid that entirely uses renewable sources for the generation of electricity. Furthermore, the decentralized generation results in a decrease in transmission losses and a lower cost of generation per kWh. In order to accommodate the varying nature of fault currents and the dynamic operating conditions of DERs, an adaptive protection scheme is proposed. This protection scheme increases the resilience of the microgrid and overcomes the shortfalls of conventional protection systems.

2. Methodology

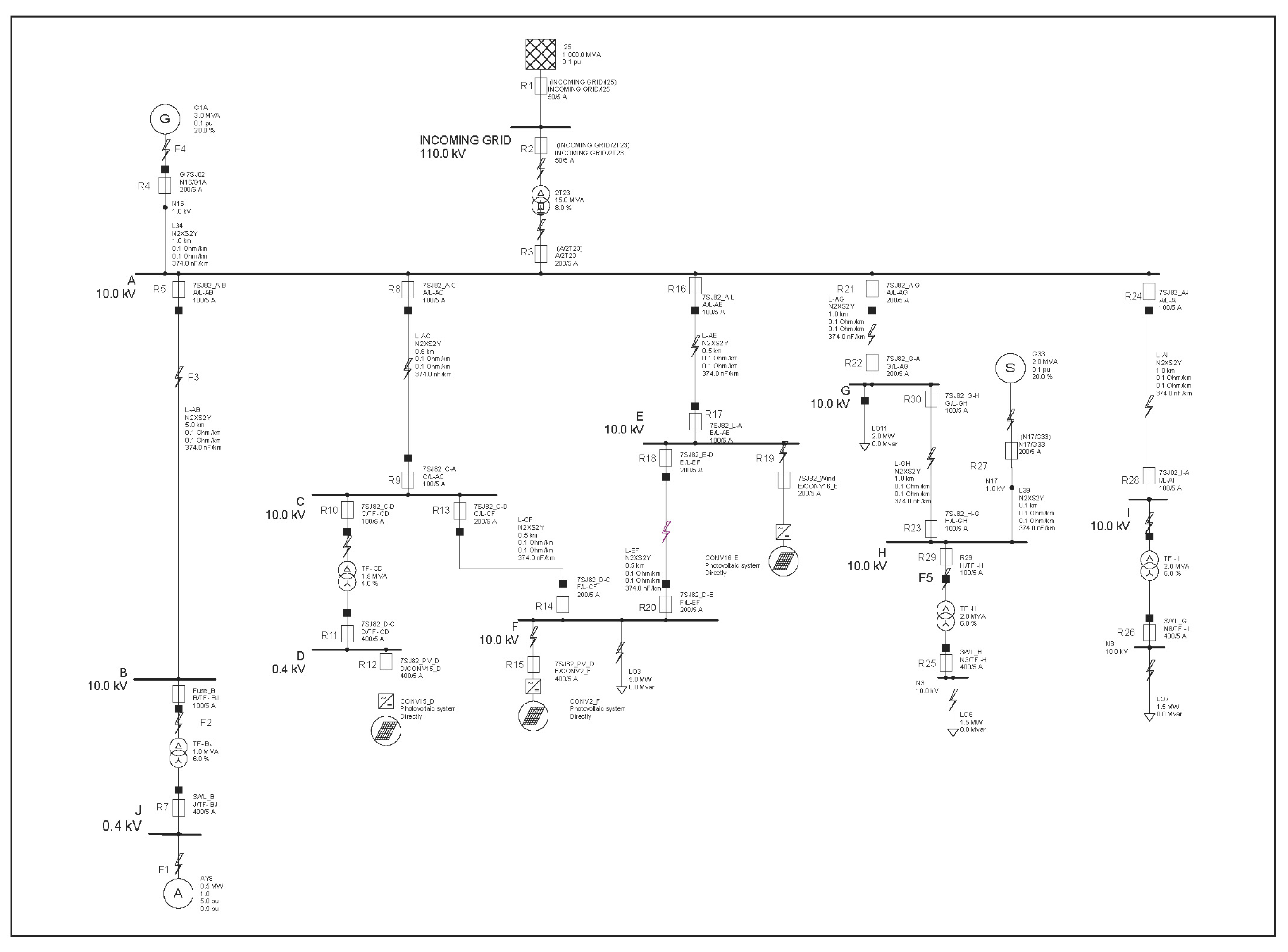
The fundamental step is the modeling of the topology of microgrids integrated with renewable sources (Photovoltaic, (PV), commonly known as solar power and hydro source). The network modeled on PSS SINCAL is shown in Figure 1.

2.1. Load Flow Analysis

In the load flow analysis [3], the proper load sharing of generators is studied, and the tolerance in voltage is taken up to the range of 5% on both the positive and negative sides. The iterative Newton–Raphson method is used for load flow analysis [4] with 99 iterations of accuracy, i.e., 0.0001 [5].

2.2. Short-Circuit Analysis

As a matter of fact, short-circuit analysis determines the steady-state solution of a linear network with a balanced three-phase excitation. In this study, a 2-phase minimum short-circuit analysis in grid-connected mode and then in islanded mode is carried out. Followed by the 3-phase maximum short-circuit analysis with both modes of operation, which helped formulate the protection strategy.

Formulation of Protection Strategy

Developing protection strategy in a power system is of utmost importance for the fundamental reason of rapidly isolating the faulty zones or the zones that contain some sort of disturbance without affecting the operation of the rest of the system.

2.3. Coordination Criteria

The coordination restriction is mentioned in Equation (1). If Ri is the primary relay for the fault at k and Rj is the backup relay for the same fault,

tj,k − ti,k ≥ ∆t

(1)

where,

• ti,k is the time of operation for the primary relay Ri for fault at point k.
• tj,k is the time of operation for the backup relay Rj for the same fault (at point k).

2.4. Relay Characteristics

2.4.1. Protection Modeling

In the proposed model, the relays used possess three states of operation. The first state is Ip stage, which is the primary stage where the relay operates in overload condition. The pickup current (Ip) is usually set with a 10–25% increase in the rated current of the device that this relay usually protects. The next stage is I>>, known as the definite stage, in which the current value is usually set to 60–70% of the 2-phase minimum short-circuit current. The time for tripping in this mode of operation is quite low, as a high fault current requires quicker tripping to avoid major damages. The third stage of relay operation is I>>>, which is also known as the instantaneous stage. The value of current at this stage is usually set to 80–90% of the short-circuit fault current. The time of operation at this stage is at least possible or nil, as it instantly trips when the fault is sensed.

2.4.2. Optimizing DOCRs (Directional Overcurrent Relays) Coordination with Genetic Algorithm

After modeling a protection scheme, genetic algorithm is implemented to optimize the Ip stage of protection relays, which follows the standard inverse function [6]. Genetic algorithm is an iterative optimization algorithm based on the genetic rule of survival of the fittest [7]. Here, it has a set of population of solutions (relay settings) that are iteratively implemented to calculate the time of operation of relay. After this, the fittest solutions are extracted, and a crossover is applied to achieve better population of the solution set. The constraints and objective function considered to minimize the overall time of tripping are discussed below.

First Constraint

To mitigate false tripping and ensure proper coordination, a primary relay must operate first during the fault occurrence. Ri is the primary relay, and Rj is the secondary relay for fault at point k. The first constraint can be formulated as shown in Equation (2)

tj,k − ti,k ≥ CTI

(2)

where

• ti,k = operating time of relay Ri for fault at point k.
• tj,k = operating time of relay Rj for fault at point k.
• CTI = current time interval.

Second Constraint

This constraint provides the minimum time of operation for a relay. Any relay cannot operate at a time less than this. The minimum operating time of all relays used in the system is 0.01 s.

Third Constraint

The tripping time of each relay depends upon its TMS (Time Multiplier Setting). Its range is 0.1–15. Genetic algorithm optimizes the TMS of relays to optimize the protection settings.

Fourth Constraint

The fourth constraint is the current setting (CS), which describes the pickup value for the relay. Its value is kept fixed and is not optimized so that the pickup value of the relay does not change.

Fifth Constraint

This is the most important constraint that determines the actual tripping time for each relay. The relay follows standard inverse, and its tripping time is optimized as shown in Equation (3).

$$t=\frac{\mathrm{T}\mathrm{M}\mathrm{S} \times 0.14}{{(\mathrm{P}\mathrm{S}\mathrm{M})}^{0.02}-1}$$

(3)

2.4.3. Objective Function

The objective function of implementing the genetic algorithm is to minimize the time of operation (top) of the relay [2]. It is achieved by optimizing the value of TMS while taking the above-mentioned constraints into consideration. It is achieved by computing the minimum possible time of operation of relay while maintaining the selective coordination criteria.

3. Results and Analysis

After completing the modeling of the network, it was validated against the standards of power system studies. The results of different studies are mentioned below.

3.1. Load Flow Studies

The results obtained after performing load flow studies on the proposed model comply with the standards defined in IEEE 3002.2TM, i.e., the bus voltages are in the range of 95–105%. Moreover, the power factor of the system is found satisfactory, i.e., 0.95 [8].

3.2. Short-Circuit Studies

The short circuit was carried out on the network in both modes of operation of the microgrid, whose results are discussed below.

3.2.1. Short-Circuit 2-Phase Minimum

For optimum relay settings, we need to find out the minimum fault current of the network. In order to achieve this, the short-circuit analysis tool of PSS SINCAL was used to carry out a 2-phase minimum short-circuit current when the microgrid was in islanded mode.

3.2.2. Short-Circuit 3-Phase Maximum

The maximum fault current of each bus was found by carrying out a 3-phase maximum short-circuit study when the microgrid was in grid-connected mode, so that the fault current contribution from the utility was also considered. The results of minimum short-circuit currents (Ifmin.) and maximum short-circuit currents (Ifmax.) are shown in

Table 1. Results of short-circuit studies.

Bus	kV Rating	Ifmin. (kA)	Ifmax. (kA)
A	10	1.21	1.67
B	10	1.03	1.46
C	10	1.19	1.65
D	0.4	16.42	24.24
E	10	1.19	1.65
F	10	1.19	1.65
G	10	1.20	1.66
H	10	1.19	1.64
I	10	1.17	1.62
J	0.4	10.45	18.88

.

3.3. Protection Coordination

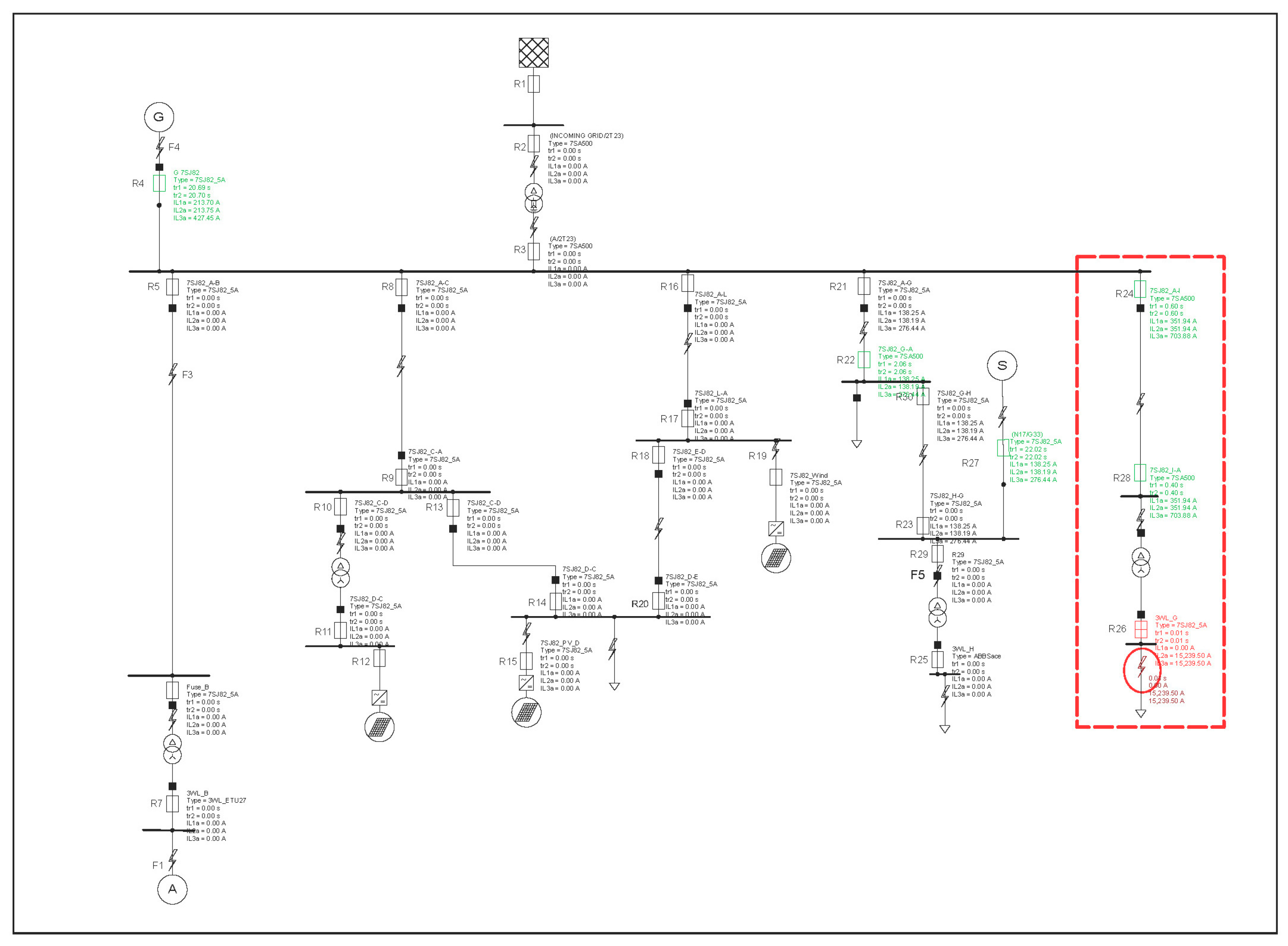
The validity of the proposed protection scheme is ensured by inserting hypothetical faults at different locations of the system. The selective tripping of relays in case of a fault at the node is shown in Figure 2.

When a fault occurred at point F3, the primary relay R26 operated instantly, while relays R24 and R28 served as the backup relays for this fault point. The other relays from which the current was flowing sensed the fault but did not become tripped, which shows that there is proper coordination between the relays.

3.4. Optimization of Relay Settings

As mentioned earlier, the relay settings are optimized by implementing a genetic algorithm using MATLAB 2018. MATLAB is an example of fourth-generation language used in research and industrial purposes [9]. The zone that is shown above is considered for the application of genetic algorithms. The comparison between old and optimized relay settings is shown in Table 2.

Table 2. Comparison between previous and optimized relay settings.

	Relay R26				Relay R28				Relay R24
	TMS	CS	Ip	Top	TMS	CS	Ip	Top	TMS	CS	Ip	Top
Before Optimization	0.15	5.95	29.75	0.555	0.2	1.27	6.35	1.36	0.4	1.384	6.92	2.98
After Optimization	0.1	5.95	29.75	0.37	0.1	1.27	6.35	0.68	0.12	1.384	6.92	0.89

Table 2. Comparison between previous and optimized relay settings.

	Relay R26				Relay R28				Relay R24
	TMS	CS	Ip	Top	TMS	CS	Ip	Top	TMS	CS	Ip	Top
Before Optimization	0.15	5.95	29.75	0.555	0.2	1.27	6.35	1.36	0.4	1.384	6.92	2.98
After Optimization	0.1	5.95	29.75	0.37	0.1	1.27	6.35	0.68	0.12	1.384	6.92	0.89

• where

• TMS = Time Multiplier Settings.
• tj,k = Coil Settings.
• Ip = Pickup of the relay.
• Top = Time of operation of the relay.

It can be seen that the value of TMS is optimized, the tripping time, “Top”, of all the relays is optimized, and the relays are working with proper coordination. The primary relay “R26” will trip first in 0.37 s. If this relay is unable to clear the fault, the relay “R28” will trip in 0.68 s and at last, relay R24 will operate if both of the above-mentioned relays are unable to clear the fault after 0.89 s.

4. Conclusions

Enhanced system reliability and efficiency are the two major benefits of inclining toward microgrids. By using renewable energy as fuel to generate carbon-free electricity, microgrids can be environmentally friendly. After modeling, the network is analyzed and then the protection settings are computed on it, which were later optimized using a genetic algorithm to achieve the best possible protection settings using MATLAB. This optimization decreases the cost of communication between the devices, which requires very complex and costly equipment.