An Optimization-Based Case Study of Aluminum Pedestrian Bridge Decks ^†

Abstract

In Sweden, steel bridges are the most common solution regarding prefabricated short-span (15–35 m) pedestrian bridges. The most common bridge type for this application is a carbon steel truss bridge with an orthotropic deck consisting of a 10–12 mm deck plate and trapezoidal stiffeners. For these bridges, the deck is the main driver regarding economic and environmental costs, originating from, e.g., high material consumption and maintenance activities. This paper aims to compare the economic aspects between a conventional steel deck and an extruded aluminum deck from an investment cost perspective. The aluminum deck is homogenous, i.e., containing no mechanical connections. To perform this case study, an optimization routine is developed and executed for the aluminum alternative. This optimization study targets the minimum weight and is constrained by the Eurocode design code. A sub-model approach is adopted for the numerical analysis, based on shell and solid elements. The procedure to go from a cross-section defined by a set of parameters to reach the optimized bridge deck is presented. The studies that are reported in this paper show that the developed optimization routine gives satisfactory results. Furthermore, they indicate that homogenous extruded aluminum decks can be a viable deck option for pedestrian bridges.

1. Introduction

In Sweden, pedestrian bridges with prefabricated superstructure are predominantly made from painted carbon steel or duplex stainless steel. Traditionally, carbon steel has been most common, but the number of stainless steel bridges has increased during recent years. The reason for an increased amount of stainless steel bridges is the increased attention to lifecycle costs. Refurbishment of the corrosion protection system of carbon steel bridges is the action dominating the in-service cost of this bridge type. Connected to the re-painting, societal costs can be substantial, dependent on the location of the bridge. In rural areas, this can have a moderate effect on the lifecycle cost. However, if the refurbishment affects vital traffic routes, the effect is substantial. Of course, this is in addition to the cost of painting, including weather protection scaffolding.

A very common bridge type for this application is the truss bridge. The two trusses are made from rectangular hollow sections and the bottom chords are connected to a traditional orthotropic bridge deck. A bridge deck consisting of a deck plate and trapezoidal stiffeners is the most common deck type. Recent studies in Sweden [1] show that the bridge deck is the dominant cost driver in this bridge type.

At present, aluminum bridges are rarely built in Sweden compared to traditional structural materials. However, historically, aluminum bridge decks have been used. However, due to high maintenance costs, many of them have been replaced to orthotropic steel decks during recent years. This is due to insufficient design and detailing. As it is known that proper detailing and design can enable durable aluminum bridges with low maintenance cost, a comparative case study in terms of investment cost is presented in this paper.

Since the material cost is a significant part of the investment cost, an optimization tool needs to be developed. One efficient way to analyze this type of bridge deck is to use finite element analysis (FEA). For the work presented in this paper, a combination of a built-in Matlab [2] genetic algorithm optimization function and a Abaqus [3], fully automated, FEA is used.

A main aim of the work that is presented in this paper is to develop a FE-based optimization routine that can be used to find optimal aluminum extrusion geometries for pedestrian bridge decks. This routine is to be constructed in such a way that it can be developed further in order to handle different cross-sections, optimization targets and bridge applications. Another main aim is to investigate the cost-efficiency of aluminum pedestrian bridge decks in comparison to traditional solutions used in Sweden. This is to be made based on investment cost, i.e., including production costs.

2. Design Basis

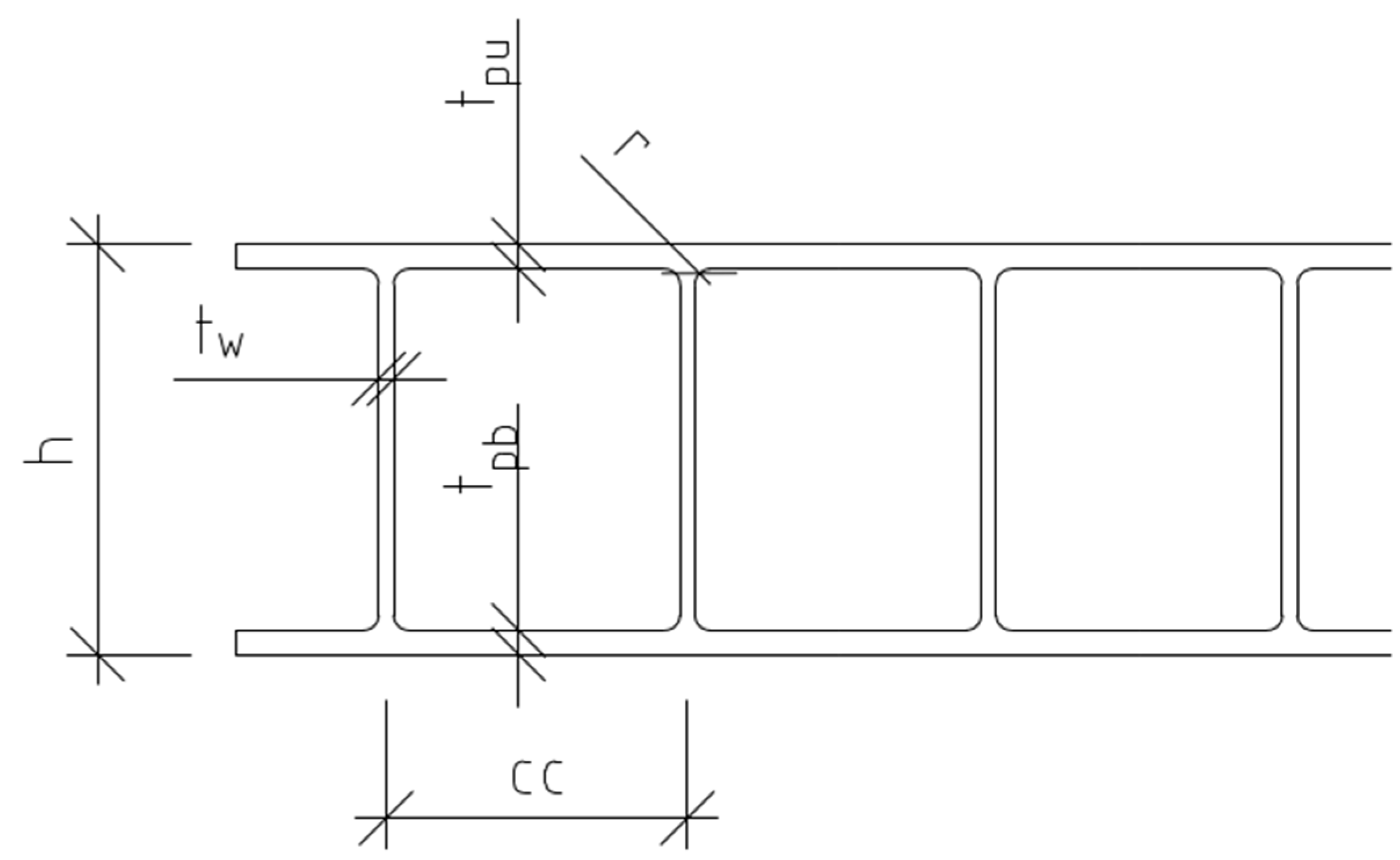
Aluminum bridge decks can take on a variety of geometrical shapes. Different shapes are investigated in [4,5,6,7,8]. The extruded sandwich sections can be formed into sandwich panels. This yields beneficial load-carrying properties. For detailed information regarding the structural behavior of sandwich structures with different types of core geometry; see [9]. Here, the rectangular cell is investigated; see Figure 1. It is defined by a set of parameters; the deck height, h; distance between webs, cc; thickness of the web, t_w; thickness of the bottom skin, t_pb; thickness of the upper skin, t_pu; corner radius, r.

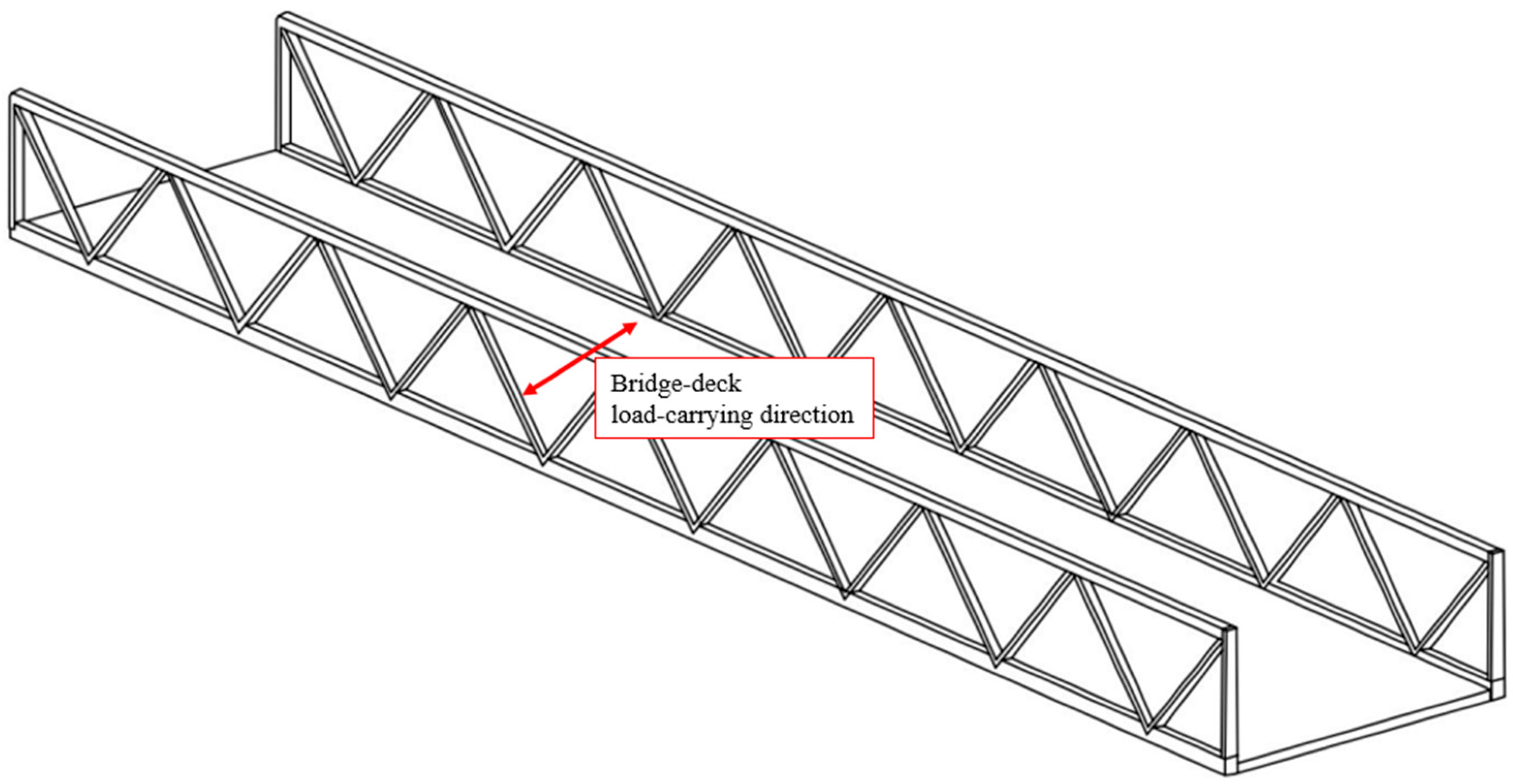
As was stated in the introduction chapter, pedestrian bridge decks are connected to a main load-carrying structure, e.g., truss beams. The bridge deck can have an orientation either in the longitudinal or transversal direction of the bridge. Here, a transversal load-carrying direction is chosen; see Figure 2. As was shown by Lindqvist and Svensson [11], the truss provides modest rotational constraint to the deck. Therefore, the deck is considered to be simply supported on two edges. The deck is considered not to be in composite action with the main load-carrying members. A bridge width of 3.5 m is used for the investigations presented in this paper.

The work presented in this paper follows the design guidelines of the Eurocodes [12] and the Swedish bridge regulations by Krav brobyggande [13]. The chosen aluminum alloy is AW-6005A-T6. The modulus of elasticity, E, is set to 70 GPa and Poisson’s ratio, ν, to 0.3. For material strength properties; see

Table 1. Material strength properties for AW-6005A-T6 (MIG-welded) [10].

Thickness t [mm]	f0 [MPa]	f0d [MPa]	fu [MPa]	f0,HAZ [MPa]	fu,HAZ [MPa]	ρ0,HAZ [MPa]	ρu,HAZ [MPa]	Buckling Class
t ≤ 5	215	195	255	115	165	0.53	0.65	A
5 < t ≥ 10	200	182	250	115	165	0.58	0.66	A

. The designing value, f_0d, is given as f₀/γ_M1, where the partial factor, γ_M1 = 1.1.

The deck design is dominated by the service vehicle load according to SS-EN 1991-2 [14]. The deck design consists of two axes, with load magnitudes of 40 and 80 kN. The service vehicle load is shown in Figure 3. As the orientation of the deck is transversal and highly orthotropic (due to low transverse shear stiffness in the weak direction), the interaction of the two axes is disregarded. Self-weight and service vehicle load are the two loads considered in this study. The validity of this assumption was verified in [10] and [11], where other loads, such as the breaking load, the crowd load and the temperature load, were shown to have a moderate impact on the deck design. The deck is designed with respect to the Ultimate Limit State (ULS) and Serviceability Limit State (SLS) requirements in [12].

For the design analysis that is presented in the coming section, a direct stress comparison between the design requirement given in [15] based on the proof strength, f₀, and the von Mises stress in the FEA is used as the design criteria. The stresses directly under the wheel pressure load are used and the axle is placed in the transversal direction of the bridge such that the wheel pressure interacts with the maximum bending in the transverse direction of the bridge. This stress check is what is used in the optimization routine. However, the final cross-section is studied in detail and verified with respect to deck deflection, the local deflection of t_pu, the shear force capacity in the web and local instability. The local deformation control is not considered as a design requirement in [12]. However, it is an aspect known to cause premature deterioration of the deck pavement. Therefore, a comparison between a steel deck design according to SS-EN 1993-2 [16] and the aluminum bridge deck is made. The only case of instability that is relevant for this application is normal stress buckling in the upper skin from bending of the deck. Therefore, verification is performed considering the cross-section class, i.e., a check of slenderness.

3. Optimization and Numerical Analysis

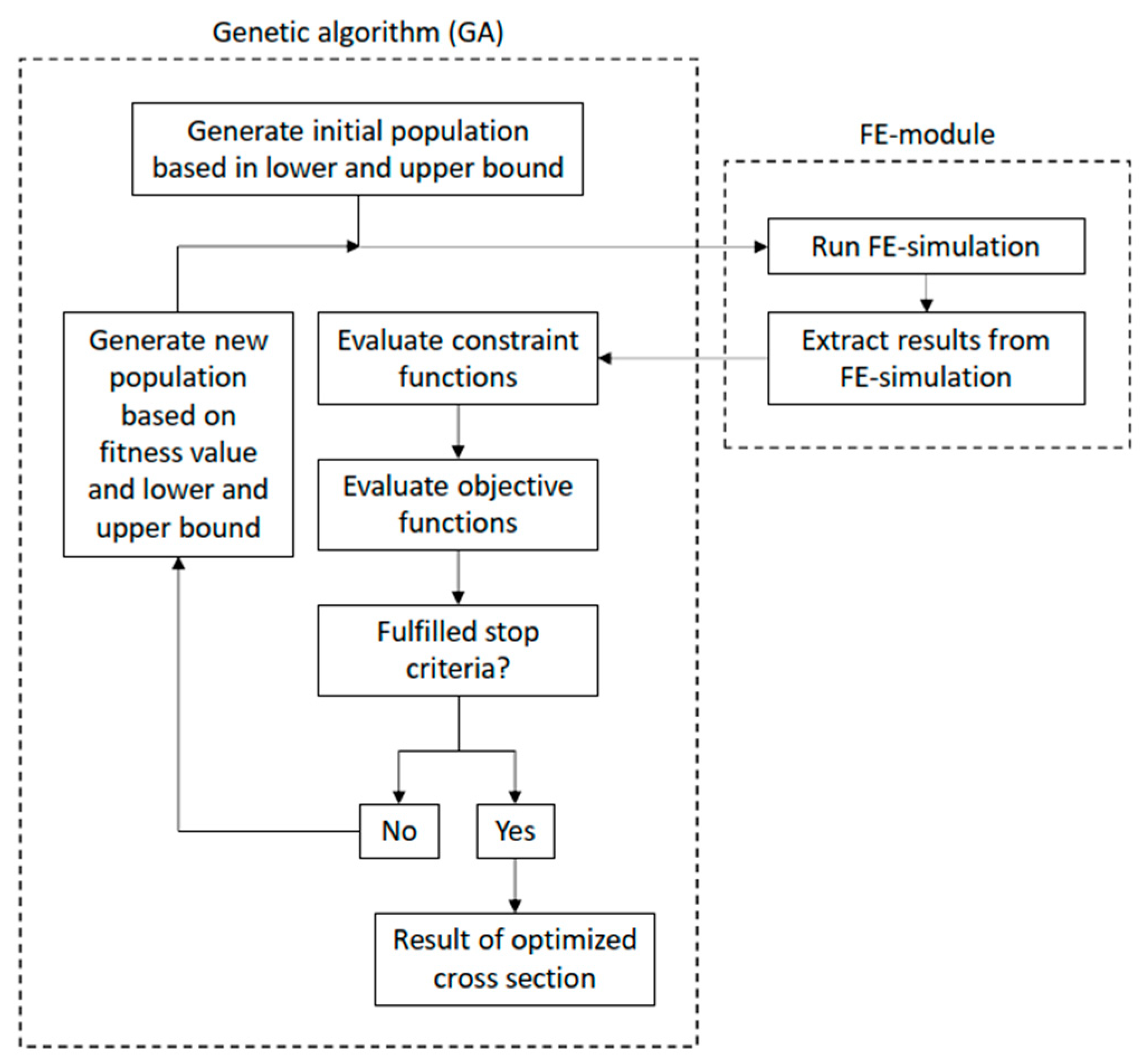
The optimization procedure is divided into two parts, a genetic algorithm optimization procedure in Matlab [2] and an FEA module in Abaqus [3]. The two parts interact in order to create a closed loop. The optimization aims to minimize the structural weight, i.e., the cross-sectional area. The decision variables for the optimization are the six parameters given in Figure 1. An overview of the optimization procedure is given in Figure 4. As genetic algorithm optimization is a stochastic process, multiple runs are needed in order to validate the results.

For each individual that is evaluated in the optimization process, a finite element analysis is run, and the resulting stresses are sent back for evaluation. This automized FEA is executed by using Python scripts that create the geometric model, apply loads and boundary conditions, create the mesh, execute the analysis and extract the resulting stresses.

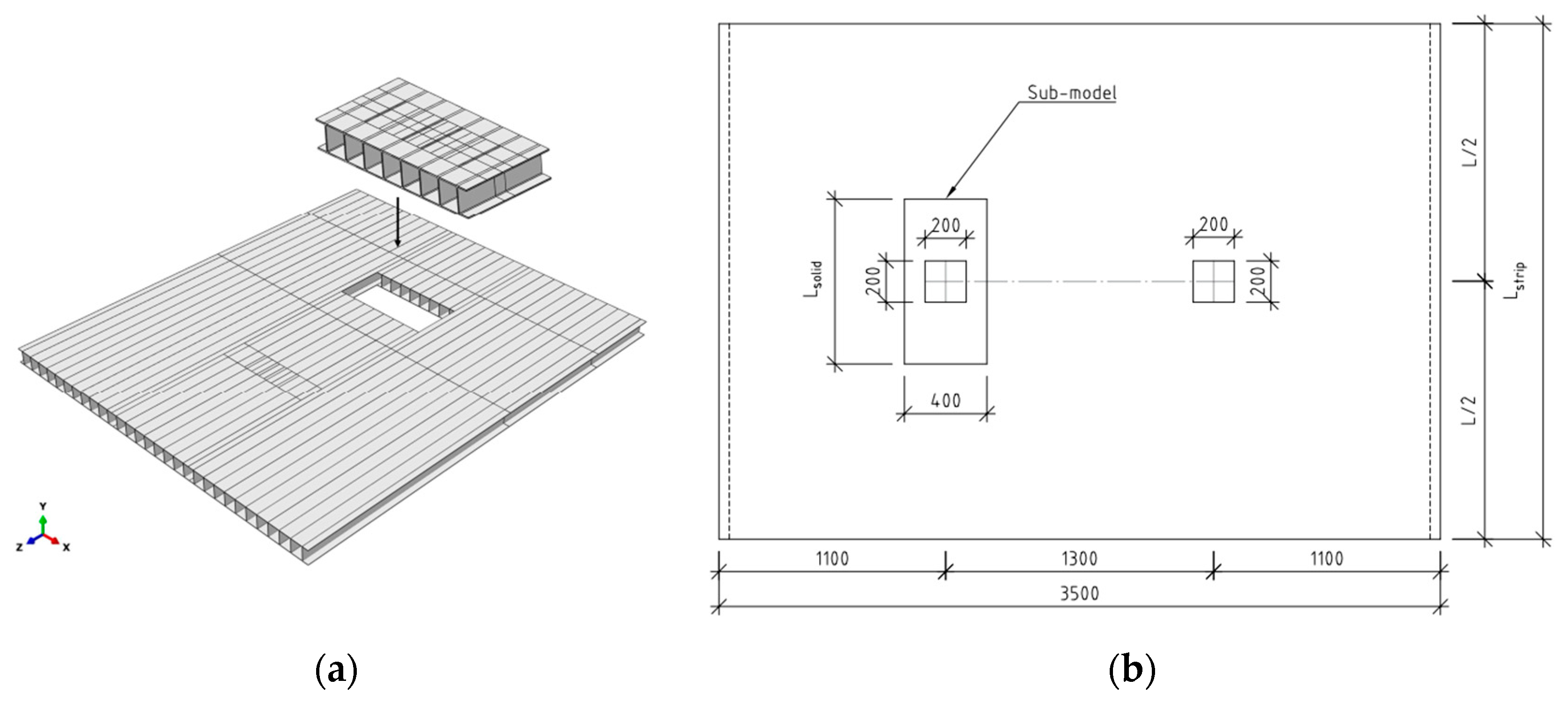
The model is a combination of shell and solid elements connected by kinematic couplings. All elements are second-order elements, i.e., 8- and 20-node elements. In the region of interest, directly under wheel pressure, solid elements are used. Shell elements are used in the surrounding areas; see Figure 5.

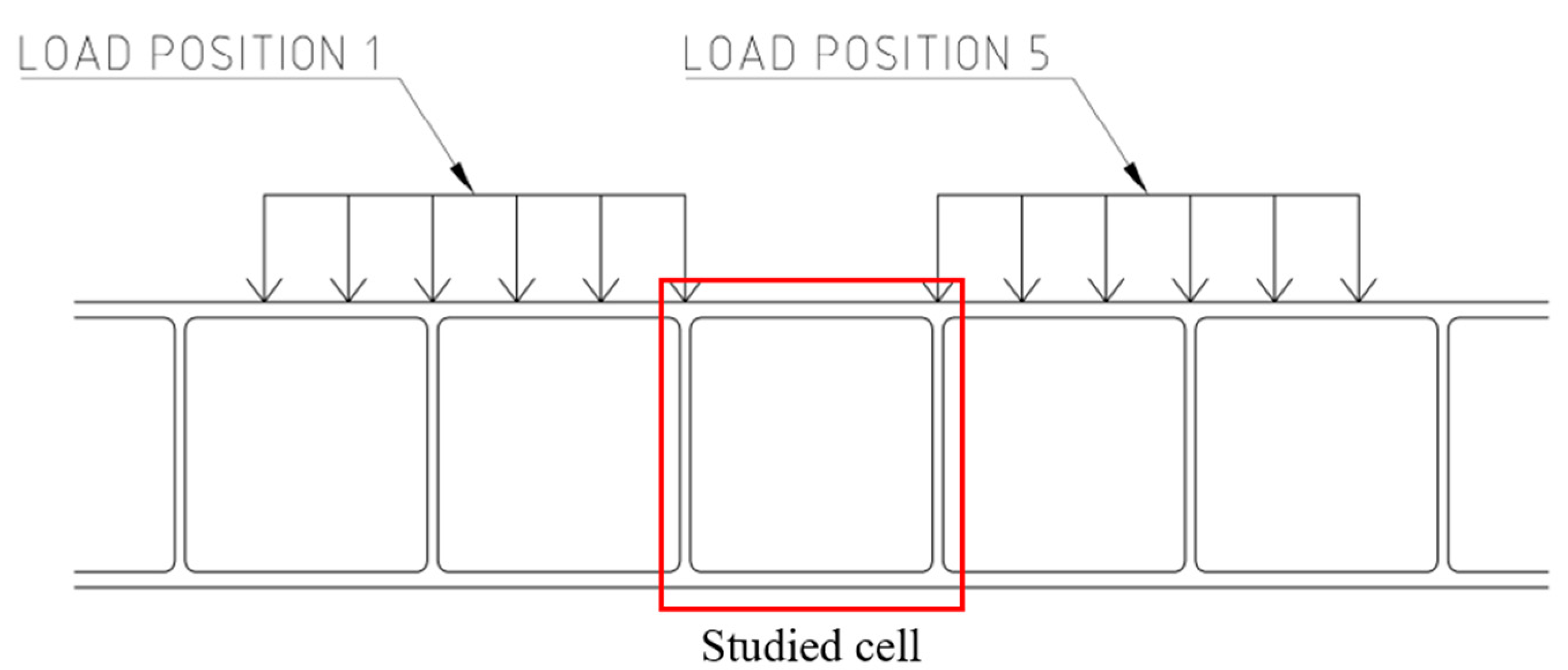
The position for designing the axis in the transverse direction is chosen such that it causes the maximal bending moment. In the longitudinal direction, five positions are tested for each FEA run in order to find the governing stress; see Figure 6. In the studied cell, the von Mises stresses are extracted from the inner and outer surface of the skins, from the inner surface of the web and from the inner surface of the corners.

The FEA is verified with respect to mesh convergence for stress and model length L in Figure 5. A model length of 3 m is used. The upper and lower bound together with the step size of the decision variables are shown in

Table 2. Upper bound, lower bound and step size in mm [10].

Variable	Domain	Variable	Domain	Variable	Domain
cc	50, 55 … 200	h	50, 60 … 200	tw	4, 5 … 8
r	1, 2 … 10	tpu	3, 4 … 8	tpb	3, 4 …8

. The productional limitations from the extrusions process are met by a geometrical constraint.

Two runs for the optimization are executed and the results are shown in

Table 3. Results from optimization analyses [10].

Variable	Optimization 1	Optimization 2
cc [mm]	65	55
r [mm]	7	8
h [mm]	60	50
tpu [mm]	5	5
tw [mm]	6	6
tpb [mm]	5	5
σmax [MPa]	180	177
A [mm2/mm]	15.26	15.36

. The two solutions give similar results: a low structural height and stocky sections as cc is small. Utilization with respect to the von Mises stress is 99% and 97% for optimizations 1 and 2, respectively. All additional design checks given in the previous section are shown to have a utilization ratio below 1; see

Table 4. Utilization of design checks [10].

Verification	Utilization Ratio [%]
Shear	80
Instability (slenderness)	Not in class 4
Deck deflection	75
Local deflection	47

. One optimization run takes approximately 6 days of analysis time, running on one local computer.

4. Cost Comparison

In order to evaluate if extruded aluminum bridge decks are an economically viable solution, a comparative study is conducted. The investment cost for the aluminum deck for a 30 × 3.5 m case is estimated by the research project LightSpan [1]. In the investment cost, the material and production costs of the deck are included. The production cost includes the cost of the extrusion of profiles, friction stir welding into panels and conventional welding of the panels into a homogenous 30 m long deck.

The aluminum deck is compared to four conventional decks out of steels S355 and S460 and stainless steels 1.4162 and 1.4462. In Swedish regulations, the stainless steels 1.4162 and 1.4462 are allowed in corrosion classes C4 and C5, respectively. C5 is for a highly corrosive environment, e.g., in costal regions with high chloride levels is the air. The investment costs for the conventional steel decks include the material and production costs. The production cost includes edge preparation, welding, mounting prior to welding, cold forming, and non-destructive testing costs. Information regarding the cost of production was gathered within the research project LightSpan [1]. Conventional steel geometries are not optimized in the same manner as the aluminum alternative but carefully chosen to be as material efficient as possible. Costs for the five investigated cases are given in

Table 5. Investment cost for five different pedestrian bridge decks [10].

Cost	S355 [kSEK]	S460 [kSEK]	1.4162 [kSEK]	1.4462 [kSEK]	AW-6005A-T6 [kSEK]
Material	165	184	394	525	175
Total	424	414	513	645	473

.

5. Concluding Remarks, Discussion and Future Research

From the work presented in this paper, it is concluded that this type of optimization procedure, incorporating several different computer programs and direct FEA stress comparison, is viable for the task at hand. However, the computational time was long. This led to the limitations of the investigation presented in previous chapters—single legation, a single extrusion profile, a large decision variable step size, etc. For future research, two main aspects will be incorporated in order to widen the scope of the investigations: a shorter analysis time for each FEA run by optimizing the developed scripts, and several individuals in the genetic algorithm will be processed simultaneously by adopting a computational cluster. This will enable a wider scope. In addition, different parametric extrusion sections and other applications, such as road vehicular bridge decks, will be enabled in future development.

The cost comparison shows that bridge decks of extruded aluminum profiles welded together by friction stir welding and conventional welding can be an economically viable option in comparison to orthotropic steel decks. A direct comparison between the duplex stainless steel solutions can be made, as both can be considered maintenance free. However, a direct connection between different aluminum legations and corrosivity class was not found in the scope of this work. Several aluminum bridges have been in service for many years, and in harsh corrosion environments, indicating that the aluminum alternative may be similar to the stainless steel alternatives. In future work, optimization studies will be executed both for conventional and aluminum solutions, considering the production cost within the optimization routine, in order to achieve refined investigations. On continuing to develop the optimization tool, by including other sections and a smaller step size for the decision variables, the aluminum deck weight and cost are expected to be further reduced.

One additional aspect of aluminum extrusions is that they are well suited for a product way of thinking, since the production cost of the tool needed for a specific cross-section is substantial. Therefore, the price per kg of bridge deck is reduced on increasing the quantity of the same extruded cross-section. The optimization procedure developed in this project can be a base for this type of product development.