Evaluation of Signal Level Distribution in 5G Radio Relay Transmissions †
Abstract
:1. Introduction
2. Use of Polarization Multiplexing
2.1. Cross-Polarization Interference Cancellation
2.2. Frequency Diversity
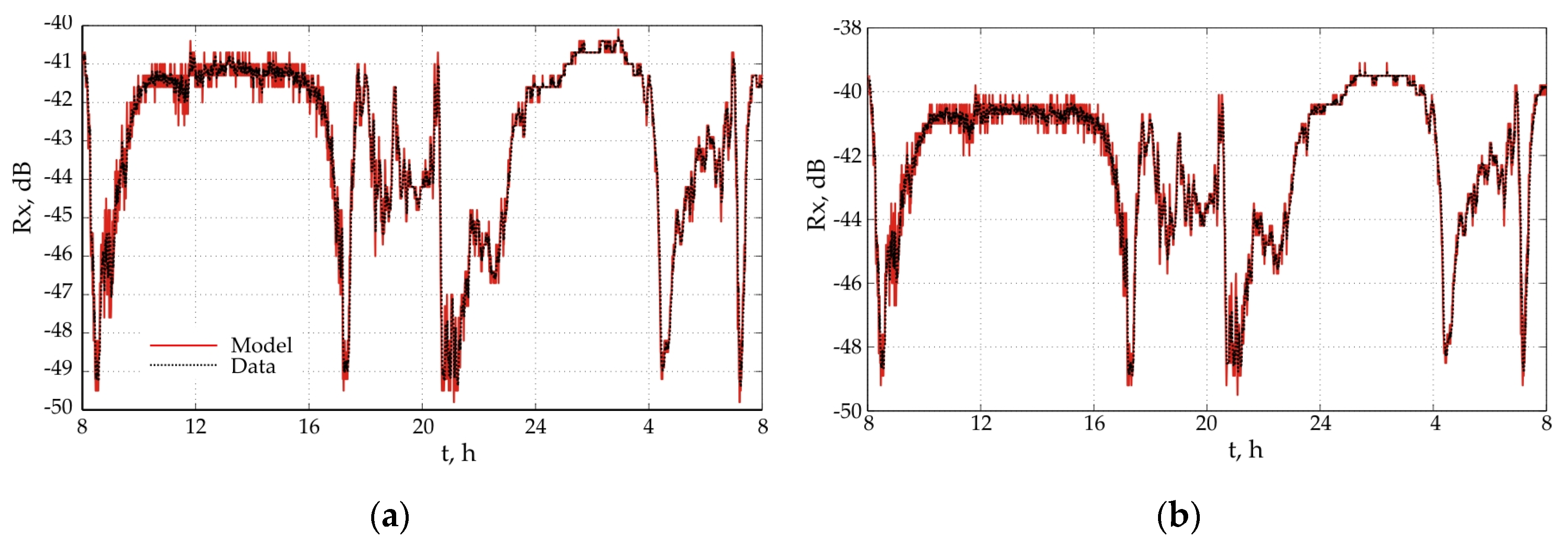
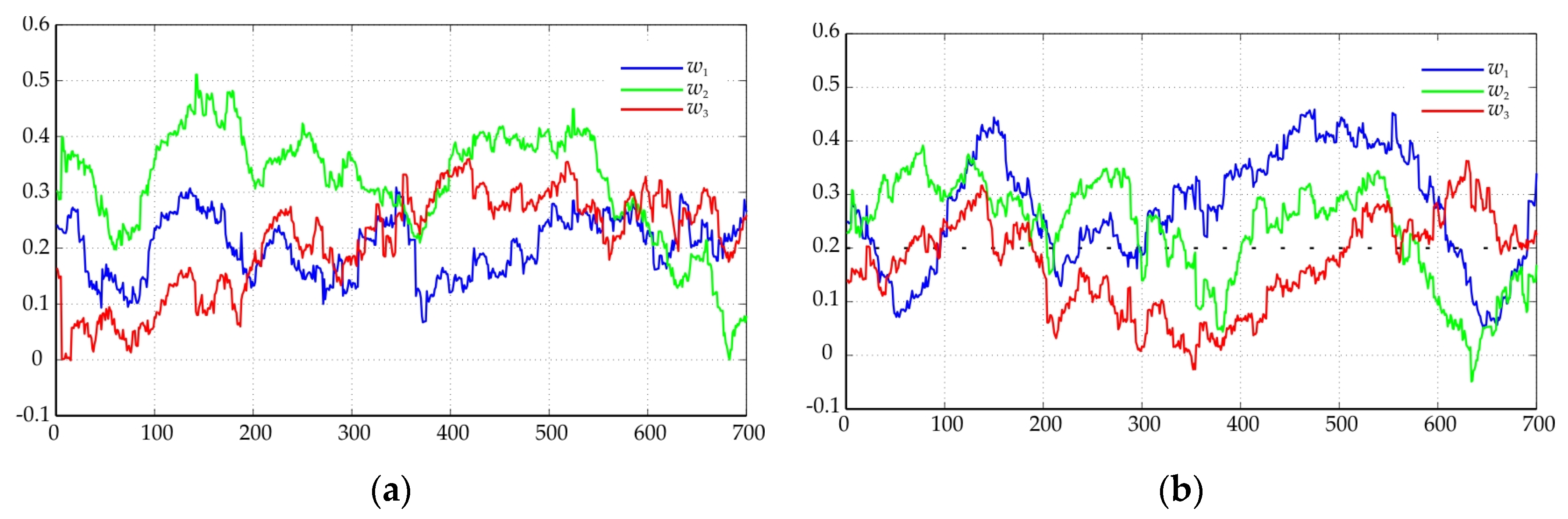
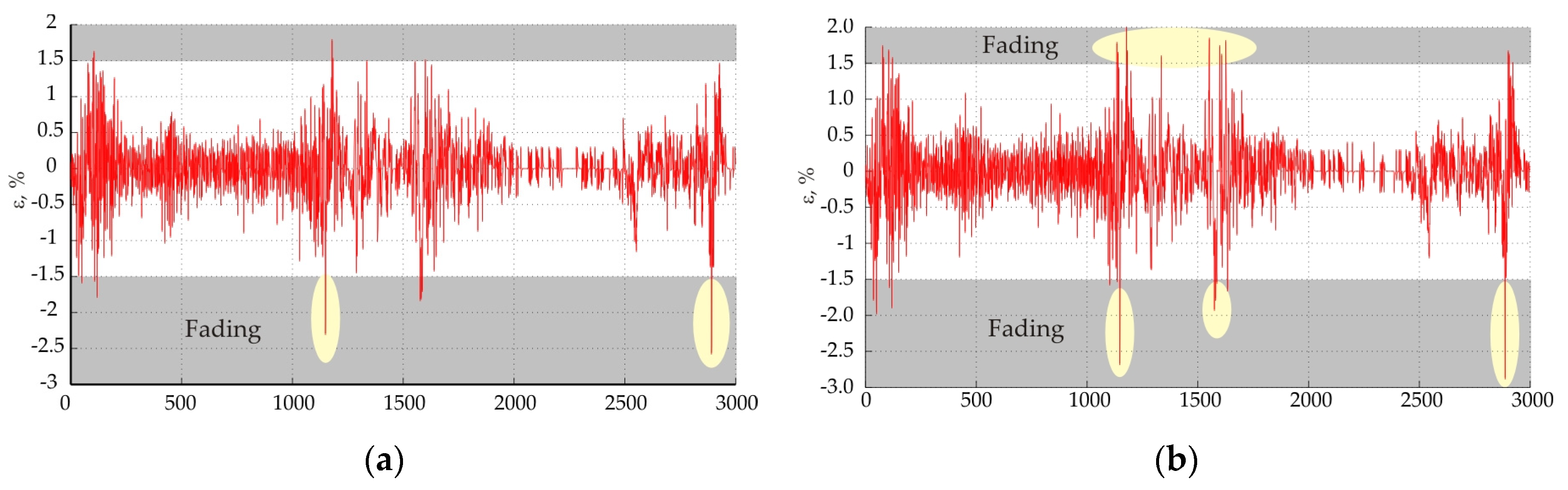
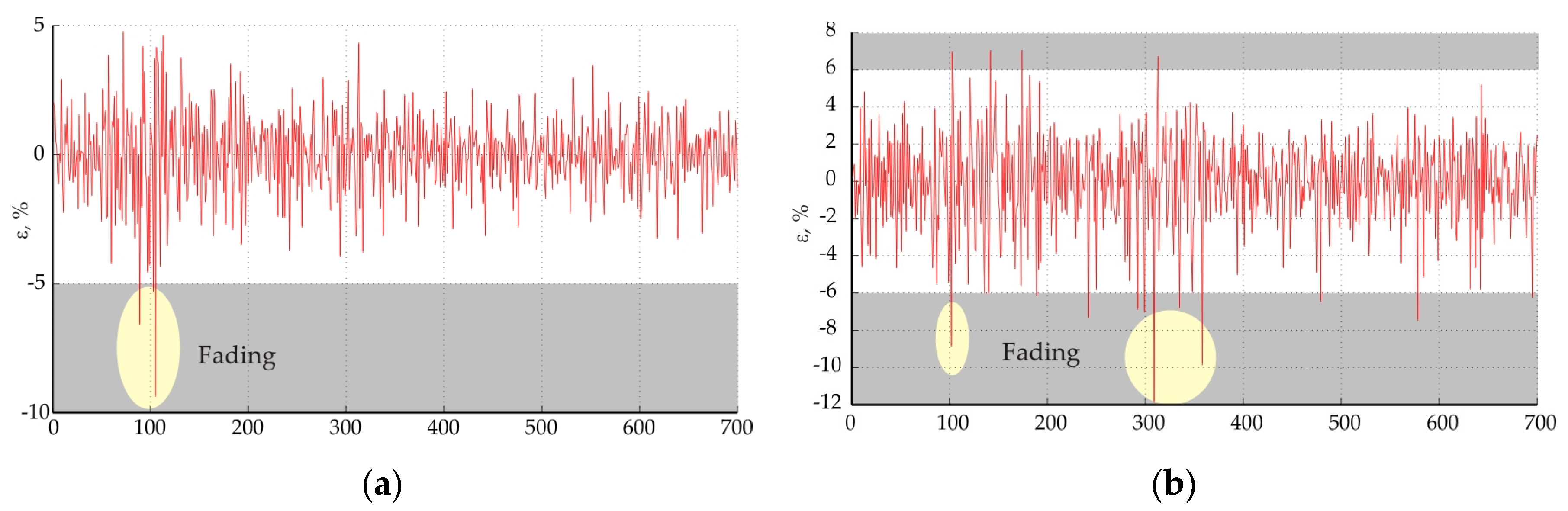
3. Analysis and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sadinov, S.M.; Angelov, K.K.; Kogias, P.G.; Malamatoudis, M.N. Approach for MIMO Wireless Channel Modelling and System Characterization for an Indoor Environment. In Proceedings of the National Conference with International Participation (TELECOM), Sofia, Bulgaria, 30–31 October 2019; pp. 54–57. [Google Scholar] [CrossRef]
- Haka, A.; Vasilev, R.; Aleksieva, V.; Valchanov, H. Simulation Framework for Building of 6LoWPAN Network. In Proceedings of the 2019 16th Conference on Electrical Machines, Drives and Power Systems (ELMA), Varna, Bulgaria, 6–8 June 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Lemeshko, O.; Lebedenko, T.; Al-Dulaimi, A. Improvement of Method of Balanced Queue Management on Routers Interfaces of Telecommunication Networks. In Proceedings of the 3rd International Conference on Advanced Information and Communications Technologies (AICT), Lviv, Ukraine, 2–6 July 2019; pp. 170–175. [Google Scholar] [CrossRef]
- Sadinov, S.; Kogias, P.; Angelov, K.; Malamatoudis, M.; Aleksandrov, A. The Impact of Channel Correlation on the System Performance and Quality of Service in 5G Networks. In Proceedings of the 7th International Conference on Energy Efficiency and Agricultural Engineering (EE&AE), Ruse, Bulgaria, 12–14 November 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Kostadinova, S.; Markova, V.; Kostov, N.; Balabanova, I.; Georgiev, G. Latency Analysis for 5G Optical Transport Network. In Proceedings of the International Conference on Biomedical Innovations and Applications (BIA), Varna, Bulgaria, 2–4 June 2022; pp. 9–12. [Google Scholar] [CrossRef]
- Liu, X.; Chen, M.; Jiang, P.; Wang, J. Research and implementation of high data rate full digital XPIC technique. In Proceedings of the 15th International Conference on Optical Communications and Networks (ICOCN), Hangzhou, China, 24–27 September 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Doubling Capacity in Wireless Channels; Provigent Inc.: Los Altos, CA, USA, November 2004; Available online: https://vdocuments.mx/xpic-tutorial.html?page=3 (accessed on 15 February 2023).
- Rencher, A.C. Methods of Multivariate Analysis; John Willey and Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Salvatore, D.; Reagle, D. Theory and Problems of Statistics and Econometrics; McGraw Hill: New York, NY, USA, 2001. [Google Scholar]
- Eshkabilov, S. Beginning MATLAB and Simulink; Apress: New York, NY, USA, 2022. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iliev, T.; Stoyanov, I.; Mihaylov, G.; Fazylova, A.; Papadopoulou, M.S. Evaluation of Signal Level Distribution in 5G Radio Relay Transmissions. Eng. Proc. 2023, 41, 2. https://doi.org/10.3390/engproc2023041002
Iliev T, Stoyanov I, Mihaylov G, Fazylova A, Papadopoulou MS. Evaluation of Signal Level Distribution in 5G Radio Relay Transmissions. Engineering Proceedings. 2023; 41(1):2. https://doi.org/10.3390/engproc2023041002
Chicago/Turabian StyleIliev, Teodor, Ivaylo Stoyanov, Grigor Mihaylov, Alina Fazylova, and Maria S. Papadopoulou. 2023. "Evaluation of Signal Level Distribution in 5G Radio Relay Transmissions" Engineering Proceedings 41, no. 1: 2. https://doi.org/10.3390/engproc2023041002
APA StyleIliev, T., Stoyanov, I., Mihaylov, G., Fazylova, A., & Papadopoulou, M. S. (2023). Evaluation of Signal Level Distribution in 5G Radio Relay Transmissions. Engineering Proceedings, 41(1), 2. https://doi.org/10.3390/engproc2023041002









