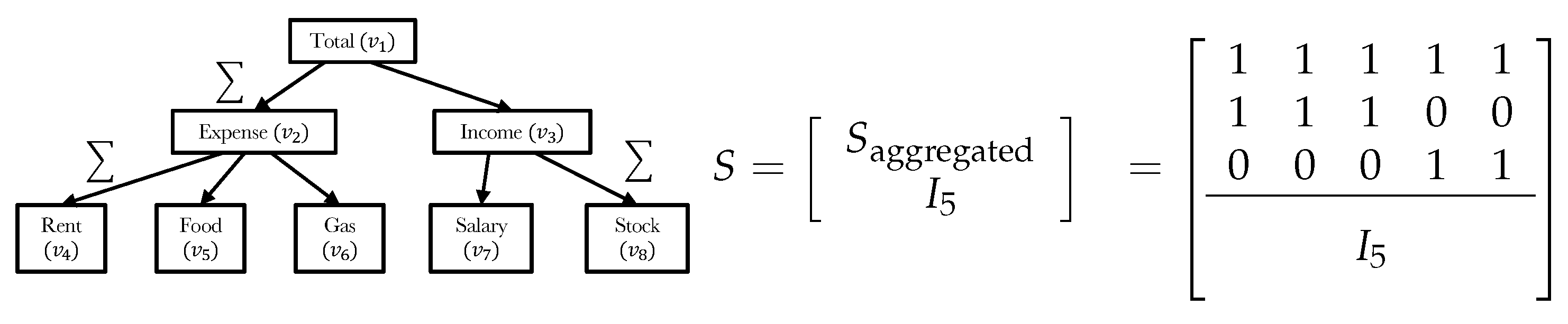Abstract
We propose a novel approach to cluster hierarchical time series (HTS) for efficient forecasting and data analysis. Inspired by a practically important but unstudied problem, we found that leveraging local information when clustering HTS leads to a better performance. The clustering procedure we proposed can cope with massive HTS with arbitrary lengths and structures. In addition to providing better insights, this method can also speed up the forecasting process for a large number of HTS. Each time series is first assigned the forecast from its cluster representative, which can be considered as “prior shrinkage” for the set of time series it represents. Then, the base forecast can be efficiently adjusted to accommodate the specific attributes of the time series. We empirically show that our method substantially improves performance for large-scale clustering and forecasting tasks involving HTS.
1. Introduction
Time series with hierarchical aggregation constraints are commonly seen in many practical scenarios [1]. In applications such as finance or e-commerce, an HTS normally represents historical records from one user (e.g., the cash flow example in Figure 1). Normally, separately building a predictive model for each user is inefficient, particularly when the number of users is quite large, or the length of user records varies significantly. To address this problem, we design a novel clustering procedure. It effectively finds the cluster representatives of a large group of HTS, followed by fine-tuning forecasts on these representatives to obtain user-specific forecasts.
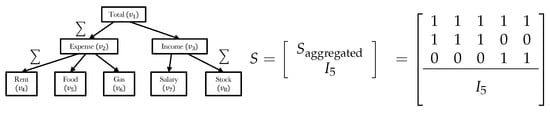
Figure 1.
Left: an example of hierarchical time series (HTS) with five bottom-level time series and three-level hierarchical structure. Each vertex () represents time series aggregated on different variables related through a domain-specific conceptual hierarchy (e.g., product categories, locations, etc.). Right: the summation matrix used to denote the given hierarchy.
Clustering time series is an important tool for discovering patterns over sequential data when categorical information is not available. Most clustering approaches fall into discriminative and generative categories. Discriminative approaches normally define a proper distance measure [2] or construct features [3] that capture temporal information. Generative approaches [4] specify the model type (e.g., HMM) a priori and estimate the parameters using maximum likelihood algorithms. Deep learning has also been applied to time series clustering. Most state-of-the-art discriminative approaches first extract useful temporal representations followed by clustering in the embedding space [5]. However, there is no prior work on clustering HTS data. This problem is more challenging since data at different level of HTS have distinct properties. Regular clustering methods for time series lead to inferior performance, particularly when the hierarchy is complex. When clustering HTS, we need to leverage level-wise information, but it is difficult to completely respect the hierarchy since the data are not easy to partition given the imposed constraints.
There is little prior work on the clustering of multilevel-structured data. A pioneering effort [6] proposed to simultaneously partition data at both local and global levels and discover latent multilevel structures. This work proposed an optimization objective for two-level clustering based on Wasserstein metrics. Its core idea was to perform global clustering based on a set of local clusters. However, this work mainly applies to discrete and semi-structured data such as annotated images and documents. It cannot be applied to HTS involving continuous or structured data, which has more constraints. A follow-up work [7] extended this to continuous data by assuming that the data at the local level is generated by predefined exponential family distributions. The authors then performed model-based clustering at both levels. However, model-based clustering for time series is computationally expensive and crucially depends on the modelling assumptions. Moreover, both these works were limited to two-level structures, whereas for several HTS applications, given a set of pre-specified features as aggregation variables, it is possible to have a multilevel hierarchy. Note that, our problem is different from hierarchical clustering [8]: the hierarchy comes from the time series data instead of the method that builds a hierarchy of clusters.
In this paper, we propose HTS-Cluster, an efficient model-free clustering method that can handle HTS with various types of individual components and hierarchies. HTS-Cluster employs a combined objective that involves clustering terms from each aggregated level. This formulation uses Wasserstein distance metrics coupled with Soft-DTW divergence [9] to cater to variable length series that are grouped together. In addition to providing superior clustering results for multilevel hierarchies, HTS-Cluster significantly improves the efficiency of forecasts when applied to large HTS datasets containing hundreds of thousands of time series.
2. Backgrounds
Hierarchical time series: Given the time stamps , let be the value of HTS at time t, where is the value of the (out of n) univariate time series. Figure 1 shows an example of HTS with a three-level structure. We refer to the time series at the leaf nodes of the hierarchy as bottom-level time series and the remaining nodes as aggregated-level time series. We split the vector of into m-bottom time series and l-aggregated time series such that where and with . The summation matrix satisfies , which can later be used to calibrate forecasting results to be aligned with a given hierarchical structure. For notational simplicity, we omit the time stamp of each series in the following discussion.
Dynamic Time Warping (DTW) [10]: DTW is a popular method for computing the optimal alignment between two time series with arbitrary lengths. Given and of length and , respectively, DTW computes the pairwise distance matrix between each time stamp and solves a dynamic program (DP) using Bellman’s recursion in time. DTW discrepancy can be used to describe the average similarity within a set of time series [2]. However, DTW is not a differentiable metric given its DP recursion nature. To address this issue, the authors of [11] proposed Soft-DTW by smoothing the operation using the log-sum-exp trick. Specifically, we assume is the alignment matrix between two time series and is the cost matrix, the formulation of the Soft-DTW can be written as
where is a parameter that controls the trade-off between the approximation and smoothness, and is the collection of all possible alignments between two time series. Soft-DTW is differentiable with respect to all of its variables and can be used for a variety of tasks such as averaging, clustering, and prediction of time series. However, Soft-DTW also has several drawbacks. Ref. [9] recently showed that Soft-DTW is not a valid divergence given its minimum is not achieved when two time series are equal; furthermore, the value of Soft-DTW is not always non-negative. Ref. [9] proposed Soft-DTW divergence, which can address these issues and achieves a better performance. This divergence can be written as
Our method incorporates the Soft-DTW divergence as a base distance measure for variable length sequences, and use it as a differentiable loss during the clustering procedure.
Wasserstein distance: For any given subset , let denote the space of Borel probability measures on . The Wasserstein space of order r of probability measures on is defined as , where denotes the Euclidean metric in . For any P or Q in , the r-Wasserstein distance between P and Q is
where contains all the joint (coupling) distributions whose margins are P and Q, and the coupling that achieves the minimum of Equation (3) is called the transportation plan. In other words, is the optimal cost of moving mass from P to Q, which is proportional to the r-power of the Euclidean distance in . Furthermore, by recursion of concepts, we define as the space of Borel measures on , then ,
Similarly, the cost of moving unit mass in its space of support is proportional to the r-power of the distance in . The Wasserstein distance can be thought of as a special case of the Wasserstein barycenter problem. Computation of the Wasserstein distance and Wasserstein barycenter has been studied by many prior works, where [12] proposed an efficient algorithm to find its local solutions. The well-known K-means clustering algorithm can also be viewed as a method to solve the Wasserstein means problem [6].
3. Hierarchical Time Series Clustering
In this section, we present the HTS-Cluster for clustering time series with both two-level and multilevel hierarchical structures. We use to denote the univariate time series of the HTS, where and . We assume the index i of each series is given by the level-order traversal of the hierarchical tree from left to right at each level. We will use and for the corresponding aggregated and bottom-level series, respectively.
3.1. Two-Level Time Series Clustering
We define a new Wasserstein distance measure as
For any , we denote the empirical measure of all bottom-level series as , where given that each HTS has at least one bottom-level series. For local (bottom-level) clustering, we assume that at most clusters can be obtained, we perform K-means that can be viewed as finding a finite discrete measure that minimizes , where is the “cluster mean” time series to be optimized in support of the finite discrete measure G and , where is the probability simplex for any .
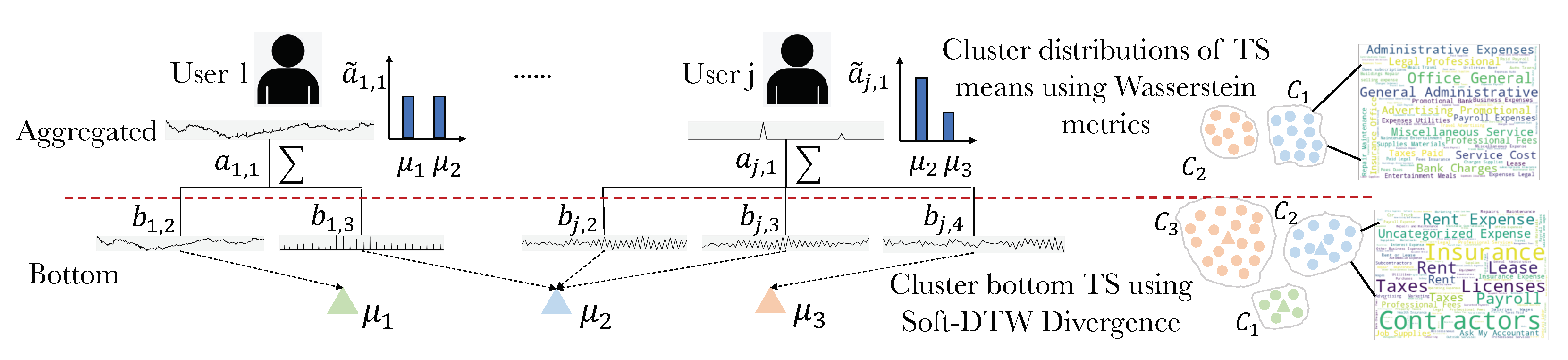
Although this approach can be extended to any aggregated level, such a method cannot leverage the connections with adjacent levels. As Figure 2 shows, aggregation of data will cause the loss of information: it is less likely to obtain reasonable results by simply clustering data at the aggregated level. Therefore, we believe that with the help of bottom-level information, clustering at the aggregated level can be further improved.
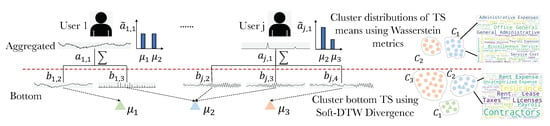
Figure 2.
Leveraging local clustering results for HTS clustering. We improve the clustering performance at the aggregated level by clustering empirical distributions over cluster representatives obtained from the bottom-level.
Problem formulation: A direct solution is to replace each top-level series with a large feature vector obtained by concatenating all bottom-level series, but this will introduce redundancy and require large training datasets due to the induced high dimensionality. Instead, we propose to leverage local information by utilizing local clustering results. For the HTS, we denote as the set that contains all descendant indices of its series, and assume each top-level series is aggregated from the bottom-level series . First, we cluster all bottom-level series into clusters with centred at . We then assign the following probability measure to each :
that is, we represent the top-level time series as an empirical distribution of , where the weight of each is determined by the number of that belongs to cluster . Note that, we distinguish from , where is its corresponding probability measure of . This formulation represents the top-level time series using a finite number of bottom-level clusters, reducing computation time from concatenating bottom-level time series while simultaneously leveraging local information. We now define the objective function to jointly optimize both local and global clusters as follows
where is the number of clusters at the top-level, and is the distribution over top-level cluster centroids. Similar to each top-level time series , the supports of are also finite discrete measures. Specifically, , where , and . Equation (6) is our formulation for the two-level HTS clustering problem, where the first term is the Wasserstein distance defined in the space of measures and the second term is defined in .
3.2. Multilevel Time Series Clustering
For HTS with multiple levels, we employ a “bottom-up” clustering procedure that recursively uses lower-level information for higher-level clustering, till the root is reached. We assume we are given N HTS with levels; we denote by a collection of the -level time series from the first N HTS and as the replacement of the corresponding time series represented by lower-level clusters. We formulate the objective function to cluster multilevel time series as
where is the total number of time series at level l among N HTS. Similarly, we have , and . Algorithm 1 shows the full procedure of the bottom-up clustering for HTS with arbitrary levels, while its core steps also apply to two-level HTS clustering. Specifically, steps 4 and 5 are the centring and cluster assignment steps for clustering time series at the (bottom) level, which uses Soft-DTW divergence as a distance measure between each input pair. After obtaining the clustering result at the -level, its cluster indices and means are used to construct probability measures for each time series at the level (step 8). Meanwhile, we still have access to the original time series in the aggregated levels. Steps 10 and 11 perform clustering in the space of probability measures. To efficiently compute the Wasserstein barycenter, we optimize the support of the barycenter , featured as the free-support method studied in [12]. For cluster assignment, we compute the Wasserstein distance between pairs of probability measures in the Soft-DTW divergence space. Both the assignment and centring steps utilize information from lower aggregation levels, where these steps are repeated until the cluster assignments are stable. We then use the results of the cluster assignment to compute the cluster means of the original time series at that level, used as supports of the probability measure to represent time series in the next aggregation level, until the clustering procedure for all levels is finished.
Computational efficiency: Compared with model-based clustering, HTS-Cluster waives the extensive computation of HMM parameters and the data assumptions. Note that, computing the Wasserstein barycenter at step 10 is very efficient since one just needs to compute the Soft-DTW divergence between the supports of each distribution, which can be obtained beforehand. The process of finding the optimal barycenter (steps 4 and 10) is differentiable. Therefore, the clustering time is progressively reduced as we proceed to higher levels.
| Algorithm 1 HTS-Cluster. |
|
HTS forecasting; Forecasts for individual HTS can “borrow strength” from the forecasts of the nearest cluster means at each level. Specifically, we first perform forecasts for the bottom- and aggregated-level cluster-mean time series and , respectively. The forecast for each time series can be represented as the weighted combination of forecasts of the corresponding cluster means at that level. We define the weight between time series i and cluster mean j at level l as
where the closer is to a certain cluster mean, the higher its weight is. Equation (8) is well known in fuzzy clustering, where a data point can belong to more than one cluster, and m is the parameter that controls how fuzzy the cluster assignments are. One can use post-reconciliation methods, such as in [1], to calibrate the results for individual forecasts.
4. Experiments
We evaluate HTS-Cluster in multiple applications. Overall, our experiments include (1) clustering time series with multilevel structures (Section 4.1); (2) facilitating time series forecasting with the help of clusters (Section 4.2).
4.1. HTS Clustering
Two-level HTS: We first conduct experiments on synthetic data using ARMA simulations, to provide a feel for the setting and the results attainable. We generate a simple HTS with two levels: one parent node with four children vertices, i.e., for the hierarchy . The length of each X is different, ranging from 80 to 300. We use the following simulation function for each time series
where is a white noise error term at time t, and c is an offset that is used to separate different clusters. We simulate four clusters, each having 30 HTS as members. Additionally, the evaluation is performed on a real-world HTS dataset containing financial records from multiple users for tax purposes. This dataset contains 12,000 users’ electronic records of expenses in different categories. The bottom-level time series are summed across all categories to obtain the total expenses. Each user owns an HTS but the length of records varies from user to user.
Multilevel HTS: We also test our method on HTS with multiple aggregated levels. It is simple to extend simulated two-level HTS to multiple levels by modifying the summation matrix S. The evaluation is also performed on a large, real-world financial dataset that contains HTS with ≥3 aggregated levels. Each HTS represents the expense records of a small business, where the bottom level (or the lowest two levels) time series are user-defined accounts (or sub-accounts), which are then aggregated by different tax purposes to obtain the middle-level time series. The top-level time series are the total expenses aggregated from the middle level, including the overall information of the business. The dataset contains 18,568 HTS with 222,989 bottom-level time series in total.
Experiment baselines: Our baselines for evaluating HTS-Cluster include the recent state-of-the-art method DTCR [5], which employs an encoder–decoder structure integrated with a fake sample generation strategy. The authors of [5] showed that DTCR can learn better temporal representations for time series data that improve the clustering performance. Here, we implement DTCR to treat HTS as regular multivariate time series data. In addition, we implemented independent level-wise clustering using Soft-DTW divergence (Soft-DTW), i.e., without local information and clustering aggregated-level data via simply concatenating lower-level time series (concat). We used three prevalent methods for clustering evaluation: normalized mutual information (NMI) [13], adjusted mutual information (AMI) [14], and adjusted rand index (ARI) [15].
Clustering results: We conducted 10 experiments, with different random seeds, on both simulated and real datasets. As shown in Table 1 (upper), for the synthetic two-level HTS, our method is superior to the baseline methods in both clustering performance and computational efficiency. Specifically, in terms of clustering performance, level-wise clustering approaches are better than DTCR, at both global (aggregated) and local (bottom) levels, since separating information from different granularities can improve the partitioning of data. As for computation time, DTCR training consists of two stages: it first learns temporal representations and then performs K-means clustering. This results in a longer computation time compared with HTS-Cluster. For level-wise approaches, clustering using Soft-DTW divergence and simple concatenation yield the same results at the bottom level, but concatenating bottom-level data provides better results at the top level since aggregation causes the loss of information. Finally, the alternating updates using the global and local cluster formulations of Equation (6), lead to improved performance due to leveraging both local and global information. Specifically, the top-level time series are represented by empirical distributions over bottom-level cluster means, and the cluster means at the top level can be obtained more efficiently via fast computation of the Wasserstein barycenter. Based on user-specified domain knowledge or constraints, we utilize the global cluster assignment to calibrate local time series that are far from the nearest cluster centre. This procedure improves both the local and global clustering results while simultaneously reducing the total computation time.

Table 1.
Level-wise clustering results on HTS with two aggregated levels. The upper part shows the results of simulated data. The lower part gives the results on real-world financial record data using a weak proxy for the cluster labels.
HTS-Cluster also demonstrates improved performance over baseline methods on multilevel HTS. As shown in Table 2, all methods are evaluated on HTS datasets with four aggregation levels, where level one is the top level and four is the bottom level. Here, HTS-Cluster employs the bottom-up procedure of Algorithm 1, where the clustering results from the lower level are leveraged for upper-level clustering until the root is reached. Therefore, the level-wise clustering methods (Soft-DTW, Concat, and HTS-Cluster) share the same results at the bottom level. At aggregated levels, HTS-Cluster consistently outperforms DTCR and Soft-DTW with the help of local information and achieves a competitive performance with Concat at a much smaller computational cost.

Table 2.
Level-wise clustering results on HTS with multiple aggregated levels. On the left are the results on simulated data while the right shows the results on real-world user financial record data. Since cluster labels are not available for the financial data, scores obtained from a weak proxy are lower than expected.
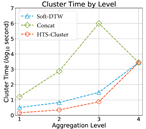
For the financial data, there are no cluster labels. Therefore, we use the “business type”, included in the metadata of each HTS, as a weak “ground truth” label for clustering. Unsurprisingly, the results metrics for all the methods are low (Table 1 bottom), and the utility of HTS-Cluster really emerges when we examine the downstream forecasting results later on. For now, to show that the clusters are still meaningful, we visualize the HTS metadata at the tax code level using our method (Figure 3). We see that HTS-Cluster does create meaningful partitions for HTS by accounting for features from a local time series. Finally, we monitor the level-wise clustering time of each method. The compared baselines include (1) level-wise clustering using Soft-DTW divergence without leveraging local clustering results; (2) simple concatenation of lower-level time series for higher-level clustering. All three methods are conducted in a bottom-up fashion, with the same bottom-level clustering procedure. As shown in Table 3 (left), HTS-Cluster provides the most efficient method for clustering aggregated-level time series. This is because (1) computing the Wasserstein barycenter at aggregated levels based on [12] is more efficient than obtaining the barycenters using Soft-DTW divergence; (2) HTS-Cluster only leverages lower-level clustering result instead of the entire set of time series at that level.

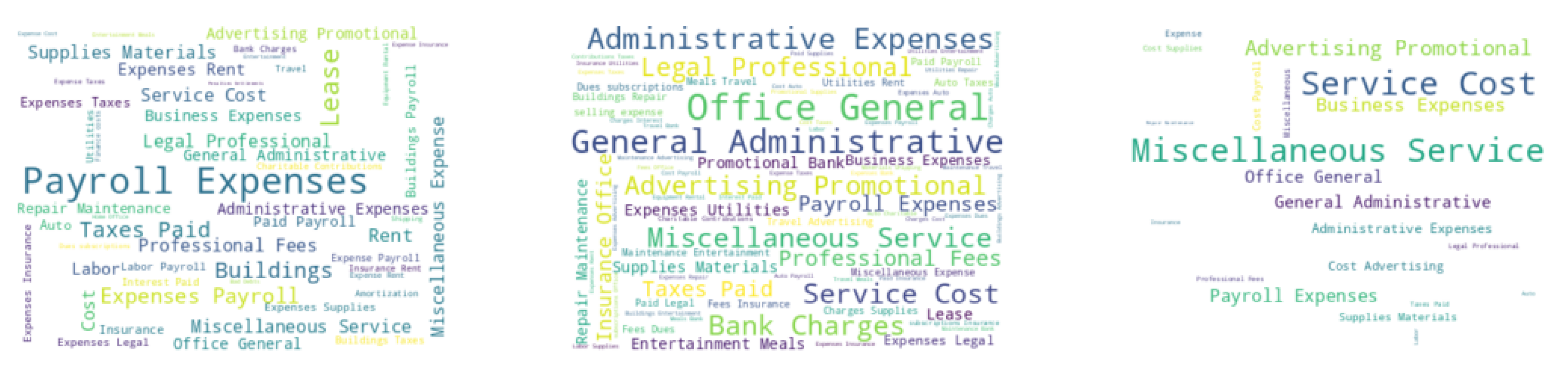
Figure 3.
Word cloud visualization of time series metadata from massive financial records. The keywords represent different types of expenses for tax purpose. The results show keywords from three representative clusters at the expense level, by leveraging the local information of clustering results obtained at the user level. The clusters provide meaningful partitions, such as “payroll expenses”, “administrative expenses”, and “service cost”, which are from distinct categories.

Table 3.
Left: level-wise computation time of different clustering approaches, DTCR is excluded since it is not a level-wise approach and requires a much longer time. Right: forecasting massive HTS with the help of clustering, results are measured by MASE and relative computing time. Results are averaged across ten runs on four-level simulated HTS.
4.2. HTS Forecasting
We propose two forecasting applications that can utilize our proposed method. We use the mean absolute scaled error (MASE) [16] to evaluate the forecasting accuracy.
Case 1: Forecast single-HTS with complex structure: Many public datasets comprise a single hierarchy that includes a large number of time series; this is common when HTS has many categorical variables to be aggregated. Forecasting a large number of correlated time series requires extensive computation for global models or parameter tuning for local models. HTS-Cluster provides an efficient way of modelling such HTS. For the bottom k-levels that have large numbers of time series, one just needs to forecast their cluster means obtained from clustering “sub-trees” at these levels. The forecasts of each time series at the bottom k-levels can be “reconstructed” using a soft combination of cluster means in Equation (8). We test our method using two popular models: DeepAR [17] and LSTNet [18] and two public HTS: Wiki and M5 [19]. In Table 4, this strategy achieves competitive results with less computation compared with the original methods. This could also improve aggregated levels without applying clustering.

Table 4.
HTS-Cluster can be used to improve HTS forecasting when a large number of forecasts are required. Results are measured by the mean absolute scaled error (MASE, the lower the better) using two multivariate time series models. Both Wiki and M5 possess a single hierarchy with many time series; we cluster “sub-trees” at the bottom two levels (out of five) of Wiki and the bottom three levels (out of twelve; we only show levels eight to twelve) of M5 to reduce the total number of time series to be modelled.
Case 2: Forecast massive HTS with simple structures: Similarly, we forecast cluster means obtained from each level of HTS, and then use Equation (8) to obtain a prediction for each HTS. To ensure forecasts are consistent with respect to the hierarchy, we apply reconciliation from [1] to the forecasts of each HTS. Table 3 shows the effectiveness of the clustering, where the total time is normalized by the method without cluster. From the results, HTS-Cluster can greatly reduce the overall computation time without compromising the forecasting accuracy.
5. Conclusions
In this paper, we addressed an important but understudied problem for clustering time series with hierarchical structures. Given that time series at different aggregated levels possess distinct properties, regular clustering methods are not ideal. We introduced a new clustering procedure for HTS such that when clustering is conducted at the same aggregated level it simultaneously utilizes clustering results from an adjacent level. In each clustering iteration, both local and global information are leveraged. Our proposed method shows improved clustering performance in both simulated and real-world HTS and proves to be an effective solution when a large number of HTS forecasting is required as a downstream task. For future work, we plan to extend this framework to model-based clustering for HTS with some known statistical properties.
Author Contributions
Conceptualization, X.H., T.R. and N.H.; methodology, X.H. and T.R.; software, X.H.; validation, X.H. and J.H.; formal analysis, X.H., T.R. and N.H.; investigation, X.H.; resources, X.H.; data curation, X.H.; writing—original draft preparation, X.H.; writing—review and editing, X.H., T.R., J.G. and N.H.; visualization, X.H.; supervision, J.G. and N.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by Intuit AI.
Data Availability Statement
This study applied a simulation dataset and open access datasets (M5 [19], Wiki https://www.kaggle.com/code/muonneutrino/wikipedia-traffic-data-exploration (accessed on 1 April 2023)), which is referenced accordingly. The financial record dataset cannot be publicly accessed due to privacy concerns.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wickramasuriya, S.L.; Athanasopoulos, G.; Hyndman, R.J. Optimal forecast reconciliation for hierarchical and grouped time series through trace minimization. J. Am. Stat. Assoc. 2019, 114, 804–819. [Google Scholar] [CrossRef]
- Petitjean, F.; Ketterlin, A.; Gançarski, P. A global averaging method for dynamic time warping, with applications to clustering. Pattern Recognit. 2011, 44, 678–693. [Google Scholar] [CrossRef]
- Aghabozorgi, S.; Shirkhorshidi, A.S.; Wah, T.Y. Time-series clustering–a decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Zhong, S.; Ghosh, J. A unified framework for model-based clustering. J. Mach. Learn. Res. 2003, 4, 1001–1037. [Google Scholar]
- Ma, Q.; Zheng, J.; Li, S.; Cottrell, G.W. Learning representations for time series clustering. Adv. Neural Inf. Process. Syst. 2019, 32, 3781–3791. [Google Scholar] [CrossRef]
- Ho, N.; Nguyen, X.; Yurochkin, M.; Bui, H.H.; Huynh, V.; Phung, D. Multilevel clustering via Wasserstein means. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1501–1509. [Google Scholar]
- Ho, N.; Huynh, V.; Phung, D.; Jordan, M. Probabilistic multilevel clustering via composite transportation distance. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, PMLR, Okinawa, Japan, 16–18 April 2019; pp. 3149–3157. [Google Scholar]
- Rodrigues, P.P.; Gama, J.; Pedroso, J. Hierarchical clustering of time-series data streams. IEEE Trans. Knowl. Data Eng. 2008, 20, 615–627. [Google Scholar] [CrossRef]
- Blondel, M.; Mensch, A.; Vert, J.P. Differentiable divergences between time series. In Proceedings of the International Conference on Artificial Intelligence and Statistics, PMLR, Virtual, 13–15 April 2021; pp. 3853–3861. [Google Scholar]
- Müller, M. Dynamic time warping. Inf. Retr. Music. Motion 2007, 69–84. [Google Scholar]
- Cuturi, M.; Blondel, M. Soft-dtw: A differentiable loss function for time-series. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 894–903. [Google Scholar]
- Cuturi, M.; Doucet, A. Fast computation of Wasserstein barycenters. In Proceedings of the International Conference on Machine Learning, PMLR, Beijing, China, 21—26 June 2014; pp. 685–693. [Google Scholar]
- Schütze, H.; Manning, C.D.; Raghavan, P. Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008; Volume 39. [Google Scholar]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Vinh, N.X.; Epps, J.; Bailey, J. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. J. Mach. Learn. Res. 2010, 11, 2837–2854. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling long-and short-term temporal patterns with deep neural networks. In Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M5 accuracy competition: Results, findings and conclusions. Int. J. Forecast. 2022, 38, 1346–1364. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).