From Matryoshka and Fukuruma to Hierarchies of Criteria and Ranking Methods in Multi-Criteria Problems of Analysis and Decision Making ^†

Abstract

Compound toys simulate the hierarchy of single inclusion. We propose classification of criteria and ranking methods for multi-criteria problems of analysis and decision making. The definitions of subjective and objective criteria are introduced. The application of two methods of cognitive visualization to identify the structure of ranking algorithms is represented: the method of separation of the ranking scheme and that of the color shading of individual elements of the scheme. A multiple-inclusion hierarchy was identified for the criteria and ranking methods. Visualization of the identified hierarchies of multiple inclusions was performed using circular representations similar to Euler–Venn diagrams. The use of objective criteria and their application in ranking algorithms was shown on the example of solving the problems of forming schedules and calendar schedules.

1. Introduction

There are several versions of the origin of the Russian matryoshka (Figure 1a). According to the most plausible version, the idea—matryoshka—was borrowed from the compound Japanese toy Fukuruma (Figure 1b). The ancient elder Fukuruma is a revered Japanese pantheon deity of the seven gods responsible for luck, happiness and prosperity. The good sage’s appearance is quite specific: an armless and legless body, shaped like an oval body-head, slightly stretched up and decorated with a beard and eyes. The eight copies inside are eight human bodies. This is allegorical, since the ancient sages believed that each person has several “shells”. In the context of this study, both the Russian matryoshka and the Japanese Fukuruma model a single-inclusion hierarchy, in which each object contains only one object of the lower level (Figure 1c). The smallest object is monolithic.

To solve practical problems, one needs to study multiple-inclusion hierarchies in which any object of a higher level can contain an arbitrary number of objects of different lower levels. That is, the multiple-inclusion hierarchy is an asymmetric analogy of the generalization hierarchy, for example, with multiple inheritances in the object-oriented programming language class hierarchy. Both toys model a person for whom decision making is one of the main forms of activity. The compound construction of toys symbolizes the possibility of decision making at each level of the hierarchy, which allows us to consider both toys as models of system analysis related to decision theory [1]. Multiple-criteria decision making (MCDM) and multiple-criteria decision analysis (MCDA) solve problems [2] of selection, comparison, classification using multi-criteria ranking methods. When studying problems in well-structured systems of various types, selection criteria are usually formed based on certain estimates (indicators, characteristics) [3] with vector and multi-vector components. A criterion is some function of a decision made. This function allows for the quantification of the feasibility of a solution. The specific value of a criterion characterizes the level of the goal achievement, as well as the effectiveness of the methods and means used in this process. If the goal generally indicates the direction of action, the criterion complements the concept of the goal and indicates an effective way to achieve it. Criteria in decision support systems can be divided into subjective, set by the decision maker (DM), and objective, depending only on the characteristics and properties of the system under study. It should be noted that MCDM and MCDA software solutions are focused on DM’s subjective criterial; therefore, they are implemented interactively. The possibility of embedding ranking algorithms in the developed software can be provided by using objective criteria. This fact requires a special analysis of ranking criteria and algorithms.

Criteria can be classified [4] as follows:

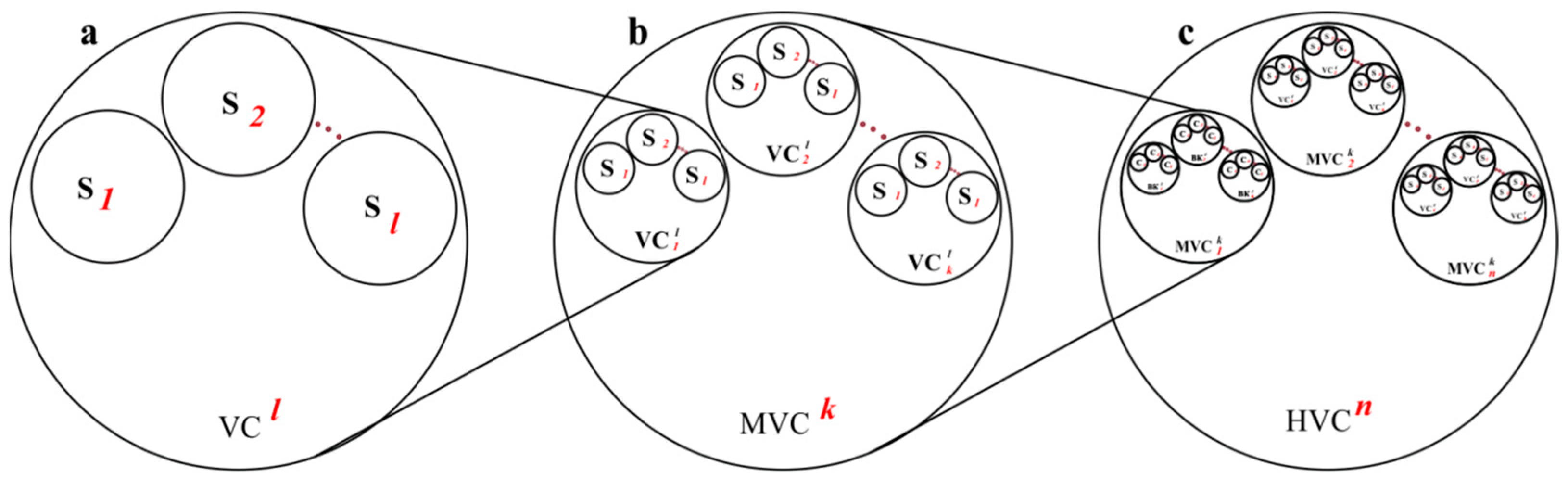
• Vector criterion—an ordered set of scalar components (estimates);
• Multi-vector criterion—an ordered set of vector criteria;
• Hypervector criterion—an ordered set of multi-vector criteria.

The proposed names of the introduced criteria are arbitrary and can be replaced with more preferred names. The criteria classification already contains an inclusion hierarchy. We also introduce the following designations:

• Scalar—S;
• Vector criterion—${VC}^l=\left\{S_i\right\},i=1,2,\dots ,l$;
• Multi-vector criterion—${MVC}^k=\left\{{VC}_i^l\right\},i=1,2,\dots ,k$;
• Hypervector criterion—${HVC}^n=\left\{{MVC}_i^k\right\},i=1,2,\dots ,n$.

To demonstrate the relationships of the criteria, the concept of Euler–Venn diagrams was used. Circular representations of criteria (Figure 2) contain criteria symbols and specified quantities of their components. Figure 2 illustrates a multiple-inclusion hierarchy in which an object of each level contains set numbers of objects of lower levels. The hierarchy of criteria inclusion can be expanded by sequentially adding new levels to form criteria with a more complex structure. For example, you can enter a supervector criterion that contains a predetermined number of hypervector criteria, etc. Structuring objects of lower levels will allow us more fully to take into account the features of the subject area of the system under study.

The study of criteria and algorithms for their ranking is associated with constantly developing multi-criteria decision-making methods [5,6] and artificial intelligence.

The purpose of this study is to analyze the structures of ranking algorithms for multi-criteria decision-making methods in systems of various types, including complex object management systems [1].

2. Methodology

The proposed approach to the analysis of criteria and structures of ranking algorithms in multi-criteria decision-making problems is based on cognitive processes. Cognitive theory covers different types of mental activities, such as observing different phenomena in the environment, pattern recognition, and problem presentation analytical reasoning. Beliefs, images, and roles can be products of cognitive processes, which are forms of heuristic judgment. One method of finding heuristic judgments is the visualization of non-trivial graphic representations [7,8]. The analysis of these representations is based on figurative thinking mechanisms. Visualizing information means transforming character data into geometric shapes that help a person form a mental image of these data.

Computer visualization is a direct route to the acquisition of information, and the application of visualization within multi-criteria methods greatly facilitates their use [3]. In this study, two approaches are considered to facilitate the perception of the features of ranking algorithms and their structure:

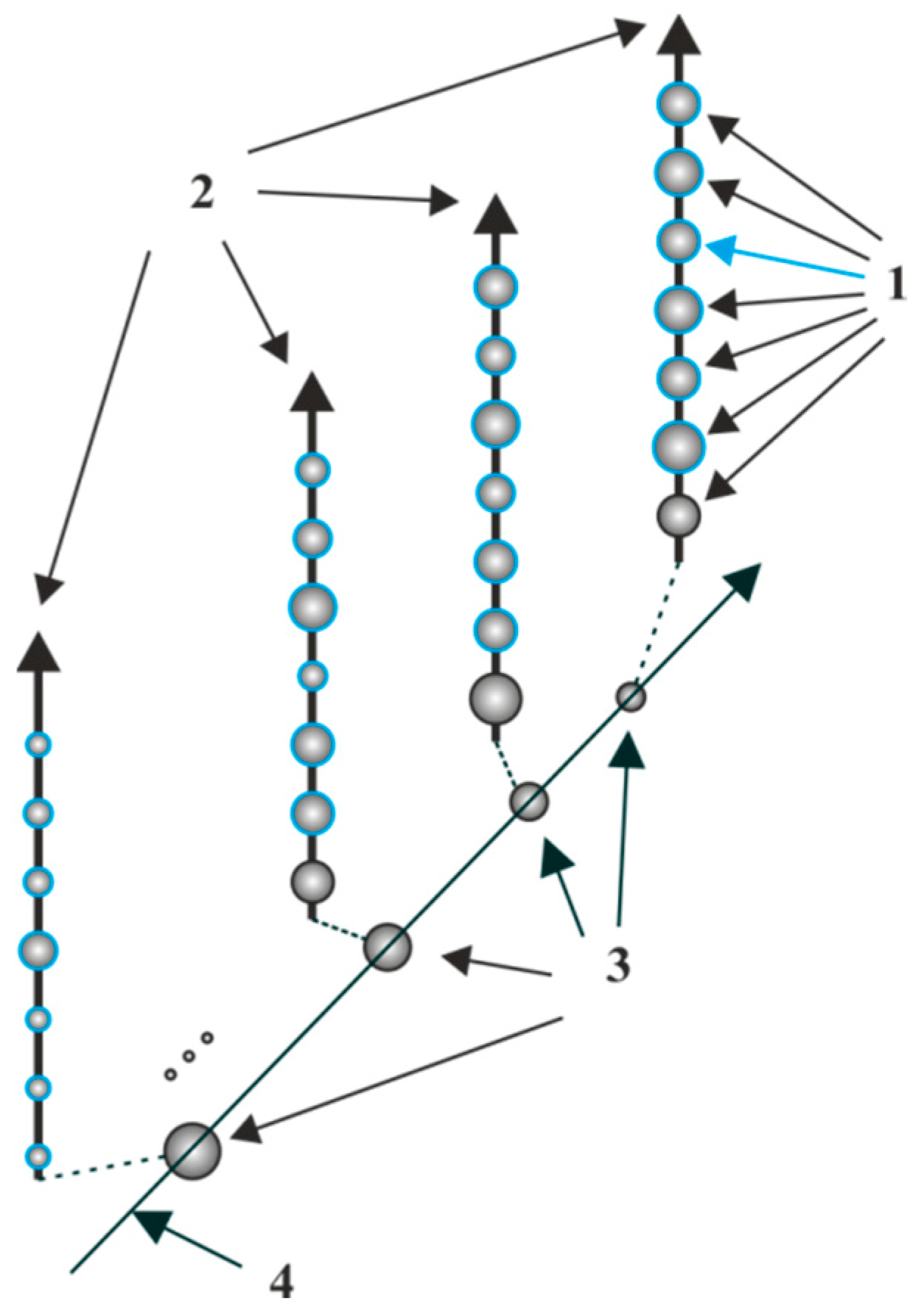
• Separating image ranked criteria and their ranks;
• Colored presentation of ranked criteria and their ranks, similar to the practice of using color plating graphs [9,10].

Examples of using criteria and ranking methods are taken from efforts to solve schedule problems of various types. Any schedule task is the task of determining the sequence of the specified actions in systems with limited resources. The formation of objective criteria in schedule tasks is based on the concepts of workload and uniformity [11]. Workload criteria represent the demand of applications or collections of applications for system resources. The uniformity criteria determine the consumption of system resources in the schedule interval. Both concepts are used in two resource-oriented scheduling strategies of different types [11]—constructive and optimizing. The first strategy is focused on obtaining an initial schedule. The second strategy optimizes the initial schedule and can be used for multi-pass solutions. Each strategy contains two priority rules. The first set of rules defines the busiest demand or set of demands or the most uneven activity or set of schedule activities. The second set of priority rules ensures uniform resource consumption when selecting timeslots for inclusion in the initial schedule in the first strategy or for permutation in the second strategy. Each priority rule uses the ranking algorithm it needs.

3. The Analysis of Ranking Methods

The results of the work of the investigated algorithms are the ranks of the criteria. The forward (ascending) and reverse (descending) ranking types will differ.

Here, we add the following symbols:

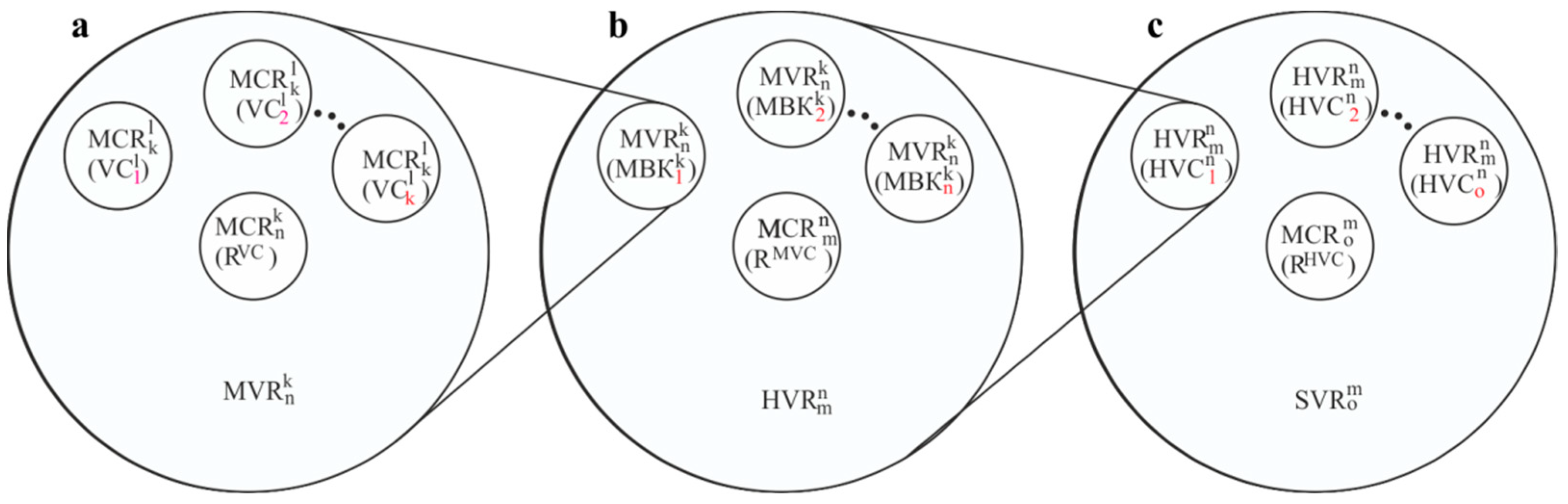
• ${MCR}_k^l\left(\right)$—multi-criterion ranking function k vector criteria ${VC}^l;$
• ${MVR}_n^k\left(\right)$—multi-vector ranking function of n multi-vector criteria ${MVC}^k;$
• ${HVR}_m^n\left(\right)$—hypervector ranking function m hypervector criteria ${HVC}^n;$
• ${SVR}_o^m\left(\right)$—supervector ranking function o supervector criteria ${SVC}^m$;
• $R^{VC}$—ordered set of ranks of vector criteria;
• $R^{MVC}$—ordered set of ranks of multi-vector criteria;
• $R^{HVC}$—ordered set of hypervector criteria.

3.1. Multicriteria Ranking

When forming the schedule of the examination session [12], each demand for the examination at the university is characterized by a vector criterion containing assessments of the workload of a group of students, a teacher and an audience. The selection of the busiest application to be included in the initial exam schedule is determined by multi-criteria ranking, i.e., ranking vector criteria containing ordered sets of scalar components.

The multi-criteria ranking is as follows.

Let there be a set of vector criteria ${VC}^l$ (Figure 3). To take into account the relative importance [13] of scalar components, it is necessary to enter a set of importance coefficients $A=\left\{a_i\right\}, i=1, 2, \dots , l$, for which the condition $\sum _{i=1}^l{a}_i=1 \mathrm{i}\mathrm{s} \mathrm{m}\mathrm{e}\mathrm{t}.$ On the basis of the analysis of results of paired comparison of the scalar component criterion values ${\left({VC}^l\right)}_k$ and ${\left({VC}^l\right)}_i$, an estimated matrix $‖C_{ki}‖$ is formed. Matrix elements $C_{ki}$ allow for the unambiguous determination of the relationship between k-th and i-th vector criteria. The values of the elements $C_{ki}$ are selected so as to further separate ineffective ones, i.e., those not included in the Pareto set solutions, from the effective ones in the estimated matrix.

For the organization of ranking of effective solutions, characteristic numbers are determined: $H_i$—the number of elements in the i-th column of the estimated matrix, the value of which is more than one; $M_i$—the number of elements in the i-th column of the same matrix, whose value is less than one; and $C_{kimax}$—the maximum value of the element in the i-th column of the matrix $‖C_{ki}‖$.

Mathematically, the meaning of the characteristic numbers is as follows:

• $H_i$ shows how many criteria from the set in question exceed the i-th criterion;
• $M_i$ shows how many criteria the i-th criterion dominates;
• $C_{kimax}$ determines how many times the k-th criterion dominates the i-th criterion.

The cyclic processing of the estimated matrix involves redefining the characteristic numbers for all columns of the estimated matrix and then determining the best criterion, for example, in the j-th column with the entry of this criterion in the Pareto tuple. After the estimated matrix processing is completed, the j-th column and the j-th row of the estimated matrix are deleted. The criteria of the Pareto tuple are “rigidly” ranked, with only the direct dominance of one criterion by another being possible. Taking this into account, the author called this method of multi-criteria ranking “rigid” ranking [4].

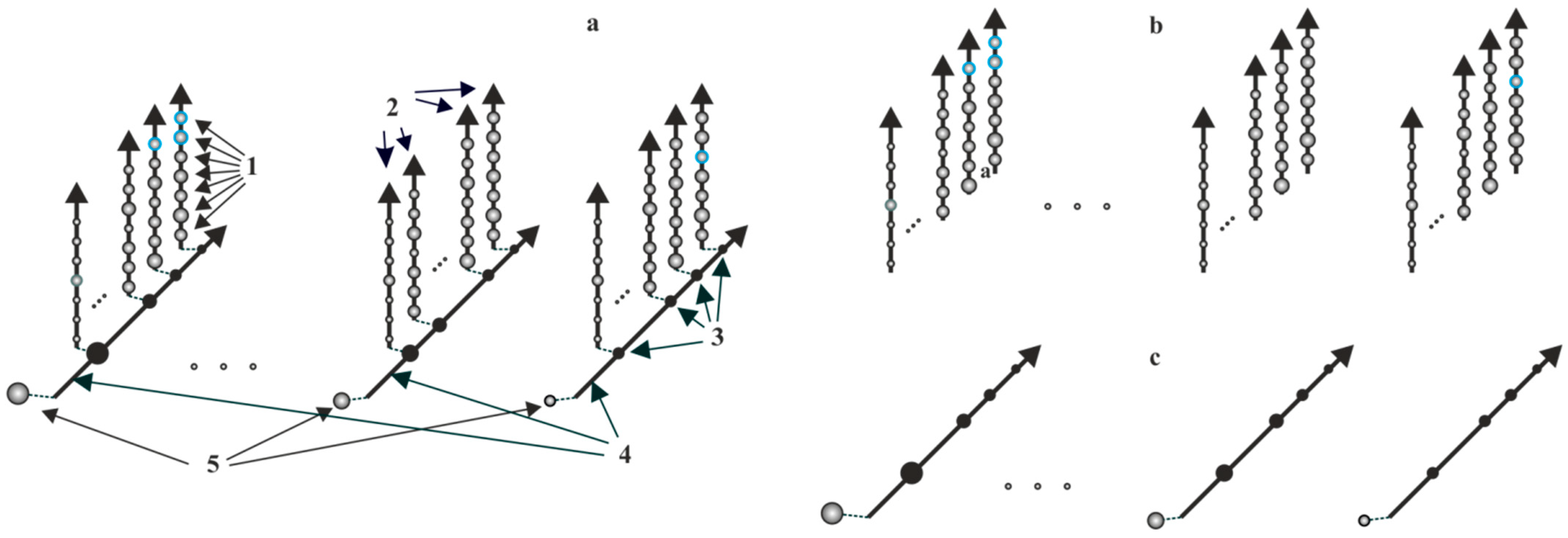
3.2. Multi-Vector Ranking

The formation of the transport schedule [14] is related to the concept of the route, that is, the sequence of loading/unloading points and the paths between these points. The route load criterion contains two vectors with load estimates of loading/unloading points and hauls, respectively. That is, the route load criterion is a multi-vector criterion. The determination of the busiest route is achieved by multi-vector ranking.

Multi-vector ranking ${MVR}_n^k$ is the ranking of multi-vector criteria ${MVC}^k$, representing ordered sets of vector criteria ${VC}^l$, with each vector criterion being an ordered set of scalar components. The analysis of the multi-vector ranking scheme (Figure 4a) allows for the division of its structure into two parts, the first of which (Figure 4b) contains all vector criteria, and with the second part (Figure 4c) there containing rank vectors $R^{VC}$ and ranks $R^{MVC}$. Figure 4c shows that ranks $R^{MVC}$ are the result of multi-criterion ranking of rank vectors $R^{VC}$. Partitioning the multi-vector ranking scheme, on the one hand, is a method of cognitive analysis, and, on the other hand, leads to the following definition. Multi-vector ranking of n multi-vector criteria with k vector criteria (Figure 4a) is performed as follows: initially k multi-criteria rankings ${MCR}_k^l\left({VC}_i^l\right), i=1, 2\dots , k$ are produced in respect to corresponding groups of vector criteria (Figure 4b) with formation of ranks $R^{VC}$ (Figure 4c); then, multi-criterion ranking of n rank vectors ${MCR}_n^k\left(R^{VC}\right)$ (Figure 4c) generates the ranks of multi-vector criteria $R^{MVC}$K^MVC (Figure 4c).

Consideration of the relative importance of criteria in multi-vector ranking is carried out as follows. For each group of vector criteria $\left({VC}_j^l\right), j=1, 2\dots , k$ multiple coefficients of scalar components are introduced: $A_i^c=\left\{a_{i,j}^c\right\},i=1, 2,\dots ,l; j=1, 2,\dots ,k,$ and $\bigvee j\sum _{i=1}^l{a}_{i,j}^c=1$, as well as many coefficients of importance of vector criteria $A_j^{VC}=\left\{a_j^{VC}\right\}, j=1, 2,\dots , k$, under a condition ${\sum }_{j=1}^k{a}_j^{BK}=1.$

3.3. Hypervector Ranking

The most complex workload criteria are the project criteria in multi-project planning [15]. Estimates of the workload demands for each type of resource form their vector loading criteria and form multi-vector loading criteria for the paths of the project graph. The set of graph path criteria generates a hypervector criterion for project load. The choice of the busiest project is determined by hypervector ranking.

Hypervector ranking ${HVR}_m^n$ is a ranking of m hypervector criteria ${HVC}^n$, representing n ordered sets of multi-vector criteria ${MVC}^k$, containing ordered sets of k vector criteria ${VC}^l$, and each vector criterion includes an ordered set of l scalar components (Figure 5). In this case, the red color plating of the ranks of the multi-vector criteria is used to identify a method for determining the ranks of hypervector criteria. This allowed us to draw the following conclusions: the ranks of multi-vector criteria (Figure 5(5)) form vectors (Figure 5(6)), the multi-criterion ranking of which determines the ranks of hypervector criteria (Figure 5(7)).

Thus, hypervector ranking ${HVR}_m^n$ includes n multi-vector rankings, defined in Section 3.2, and multi-criterion ranking of multi-vector criteria rank vectors ${MCR}_n^k\left(R^{VC}\right)$ with the formation of hypervector criteria ranks. Consideration of the relative importance of criteria in hypervector ranking is as follows. In each group of multi-vector criteria (${MBK}_j^k, j=1, 2,\dots , n$), the actions presented in Section 3.2 are performed. A plurality of importance coefficients of the multi-vector criteria $A_j^{MVC}=\left\{a_j^{MVC}\right\}, j=1, 2,\dots , n$, under a condition ${\sum }_{j=1}^n{a}_j^{MVC}=1$.

4. Some Considerations about Ranking Criteria and Methods

The results obtained in Section 3.2 and Section 3.3 provide the basis for a geometric interpretation of the hierarchy of ranking methods (Figure 6). The hierarchy diagram of multiple inclusions of ranking methods, which is also a criteria diagram (Figure 2), contains circular representations. The diagram includes the forecast of the supervector ranking method (Figure 6c).

5. Conclusions

As a result of the analysis of ranking criteria and methods, the following judgments are made:

• Classification of criteria and ranking methods for multi-criteria problems of analysis and decision making is proposed.
• A multiple-inclusion hierarchy is identified for the criteria and ranking methods.