Enhancing Phase Measurement by a Factor of Two in the Stokes Correlation †
Abstract
:1. Introduction
2. Theory
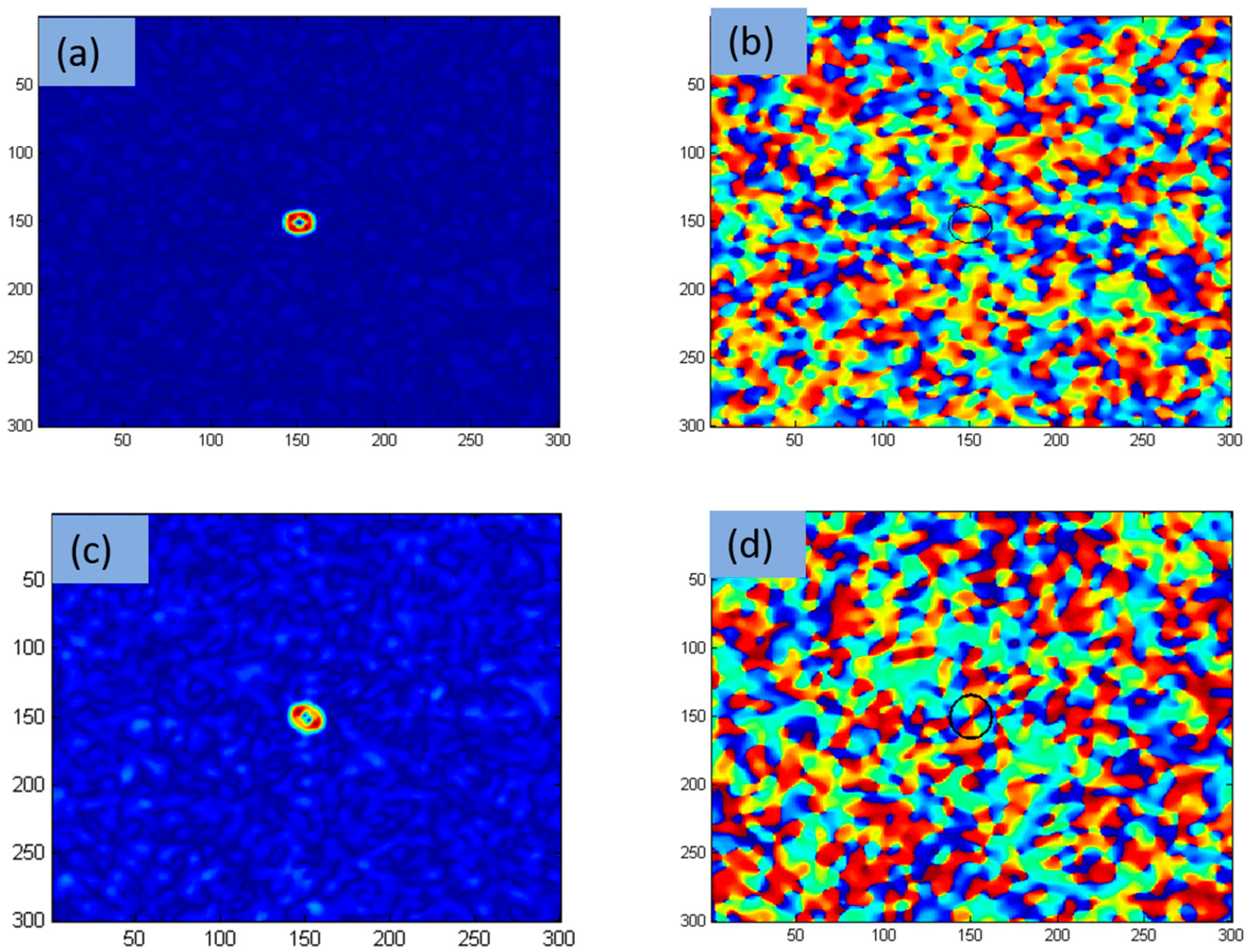
3. Result and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Groot, P.J. A review of selected topics in interferometric optical metrology. Rep. Prog. Phys. 2021, 82, 056101. [Google Scholar] [CrossRef] [PubMed]
- Creath, K. V Phase-Measurement Interferometry Techniques. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 1988; Volume 26, pp. 349–393. [Google Scholar]
- Shirai, T. Phase difference enhancement with classical intensity interferometry. Opt. Commun. 2016, 380, 239–244. [Google Scholar] [CrossRef]
- Singh, R.K.; Vinu, R.V.; Sharma, A.M. Recovery of complex valued objects from two-point intensity correlation measurement. Appl. Phys. Lett. 2014, 104, 111108. [Google Scholar] [CrossRef]
- Kuebel, D.; Visser, T.D. Generalized Hanbury Brown-Twiss effect for Stokes parameters. J. Opt. Soc. Am. 2019, 36, 362. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, T.; Parvin, R.; Brundavanam, M.M.; Kumar Singh, R. Higher-order Stokes-parameter correlation to restore the twisted wave front propagating through a scattering medium. Phys. Rev. A 2021, 104, 013525. [Google Scholar] [CrossRef]
- Huang, P.S.; Zhang, S. Fast three-step phase-shifting algorithm. Appl. Opt. 2006, 45, 5086–5091. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yadav, A.; Sarkar, T.; Suzuki, T.; Singh, R.K. Enhancing Phase Measurement by a Factor of Two in the Stokes Correlation. Eng. Proc. 2023, 34, 4. https://doi.org/10.3390/HMAM2-14273
Yadav A, Sarkar T, Suzuki T, Singh RK. Enhancing Phase Measurement by a Factor of Two in the Stokes Correlation. Engineering Proceedings. 2023; 34(1):4. https://doi.org/10.3390/HMAM2-14273
Chicago/Turabian StyleYadav, Amit, Tushar Sarkar, Takamasa Suzuki, and Rakesh Kumar Singh. 2023. "Enhancing Phase Measurement by a Factor of Two in the Stokes Correlation" Engineering Proceedings 34, no. 1: 4. https://doi.org/10.3390/HMAM2-14273
APA StyleYadav, A., Sarkar, T., Suzuki, T., & Singh, R. K. (2023). Enhancing Phase Measurement by a Factor of Two in the Stokes Correlation. Engineering Proceedings, 34(1), 4. https://doi.org/10.3390/HMAM2-14273





