Advanced Imaging Methods Using Coded Aperture Digital Holography †
Abstract
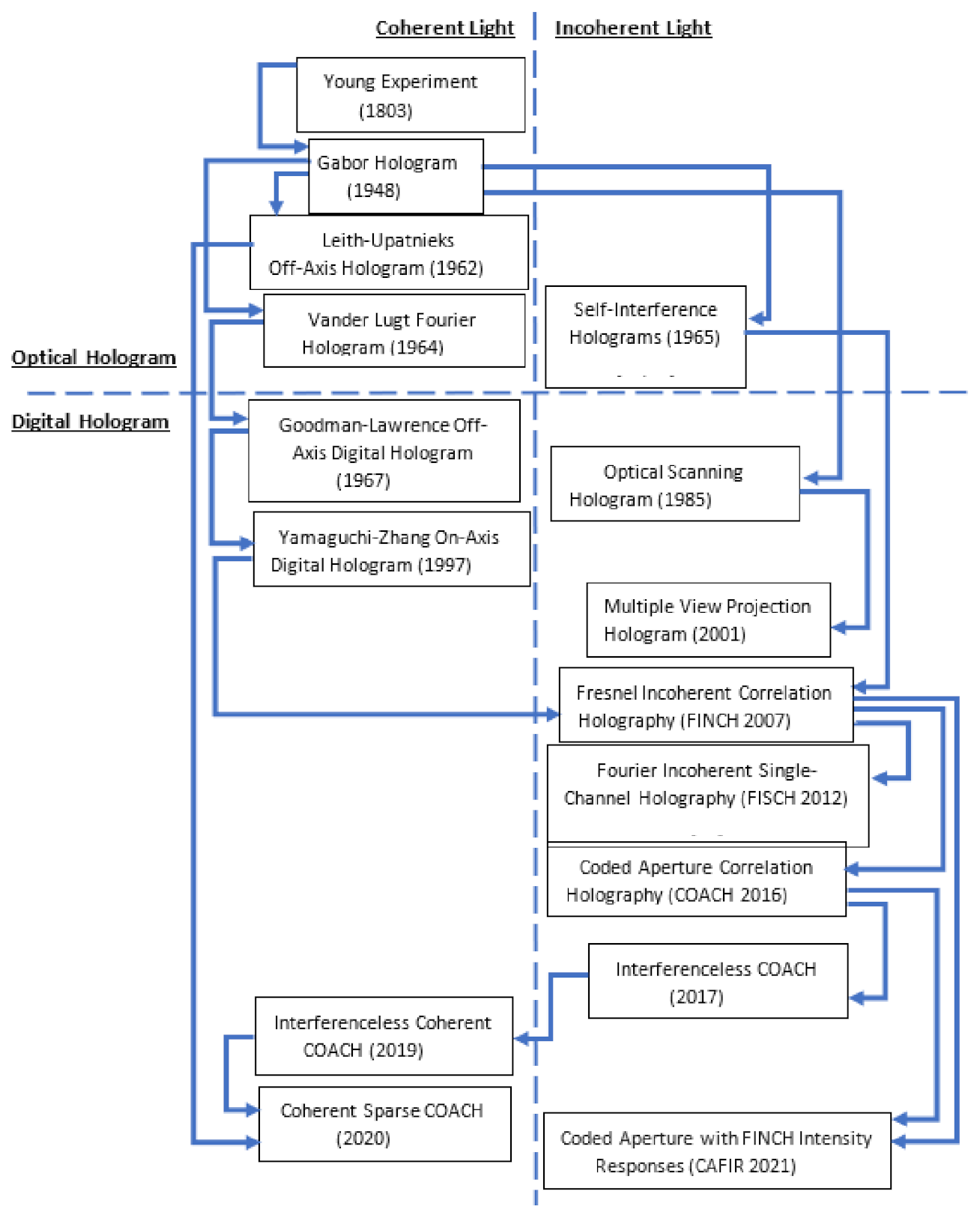
:1. Introduction
2. Coded Aperture Correlation Holography (COACH)
3. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tahara, T.; Zhang, Y.; Rosen, J.; Anand, V.; Cao, L.; Wu, J.; Koujin, T.; Matsuda, A.; Ishii, A.; Kozawa, Y.; et al. Roadmap of incoherent digital holography. Appl. Phys. B 2022, 128, 193. [Google Scholar] [CrossRef]
- Sheridan, J.T.; Kostuk, R.K.; Gil, A.F.; Wang, Y.; Lu, W.; Zhong, H.; Tomita, Y.; Neipp, C.; Francés, J.; Gallego, S.; et al. Roadmap on holography. J. Opt. 2020, 22, 123002. [Google Scholar] [CrossRef]
- Javidi, B.; Carnicer, A.; Anand, A.; Barbastathis, G.; Chen, W.; Ferraro, P.; Goodman, J.; Horisaki, R.; Khare, K.; Kujawinska, M.; et al. Roadmap on digital holography. Opt. Express 2021, 29, 35078–35118. [Google Scholar] [CrossRef] [PubMed]
- Braat, J.; Lowenthal, S. Short-exposure spatially incoherent holography with a plane-wave illumination. J. Opt. Soc. Am. 1973, 63, 388–390. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Wang, Y. Self-reference hologram. Proc. SPIE 2008, 6837, 68371. [Google Scholar]
- Leith, E.; Upatnieks, J. Reconstructed Wavefronts and Communication Theory. J. Opt. Soc. Am. 1962, 52, 1123–1130. [Google Scholar] [CrossRef]
- Stoykova, E.; Kang, H.; Park, J. Twin-image problem in digital holography-a survey (Invited Paper). Chin. Opt. Lett. 2014, 12, 060013. [Google Scholar] [CrossRef]
- Lohmann, A.W. Wavefront reconstruction for incoherent objects. J. Opt. Soc. Am. 1965, 55, 1555–1556. [Google Scholar] [CrossRef]
- Stroke, G.W.; Restrick, R.C. Holography with spatially noncoherent light. Appl. Phys. Lett. 1965, 7, 229–231. [Google Scholar] [CrossRef]
- Rosen, J.; Vijayakumar, A.; Kumar, M.; Rai, M.R.; Kelner, R.; Kashter, Y.; Bulbul, A.; Mukherjee, S. Recent advances in self-interference incoherent digital holography. Adv. Opt. Photon. 2019, 11, 1–66. [Google Scholar] [CrossRef]
- Bryngdahl, O.; Lohmann, A. Variable magnification in incoherent holography. Appl. Opt. 1970, 9, 231–232. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W.; Lawrence, R.W. Digital image formation from electronically detected holograms. Appl. Phys. Lett. 1967, 11, 77–79. [Google Scholar] [CrossRef]
- Balasubramani, V.; Kujawińska, M.; Allier, C.; Anand, V.; Cheng, C.-J.; Depeursinge, C.; Hai, N.; Juodkazis, S.; Kalkman, J.; Kuś, A.; et al. Roadmap on Digital Holography-Based Quantitative Phase Imaging. J. Imaging 2021, 7, 252. [Google Scholar] [CrossRef] [PubMed]
- Vander Lugt, A. Signal detection by complex spatial filtering. IEEE Trans. Inf. Theory 1964, IT-10, 139–145. [Google Scholar] [CrossRef]
- Yamaguchi, I.; Zhang, T. Phase-shifting digital holography. Opt. Lett. 1997, 22, 1268–1270. [Google Scholar] [CrossRef]
- Guel-Sandoval, S.; Ojeda-Castañeda, J. Quasi-Fourier transform of an object from a Fresnel hologram. Appl. Opt. 1979, 18, 950–951. [Google Scholar] [CrossRef] [PubMed]
- Poon, T.-C. Scanning holography and two-dimensional image processing by acousto-optic two-pupil synthesis. J. Opt. Soc. Am. A 1985, 2, 521–527. [Google Scholar] [CrossRef]
- Poon, T.-C.; Doh, K.B.; Schilling, B.W.; Wu, M.H.; Shinoda, K.K.; Suzuki, Y. Three-dimensional microscopy by optical scanning holography. Opt. Eng. 1995, 34, 1338–1344. [Google Scholar] [CrossRef]
- Li, Y.; Abookasis, D.; Rosen, J. Computer-generated holograms of three-dimensional realistic objects recorded without wave interference. Appl. Opt. 2001, 40, 2864–2870. [Google Scholar] [CrossRef]
- Shaked, N.T.; Katz, B.; Rosen, J. Review of three-dimensional imaging by multiple-viewpoint-projection based methods. Appl. Opt. 2009, 48, H120–H136. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.; Brooker, G. Digital spatially incoherent Fresnel holography. Opt. Lett. 2007, 32, 912–914. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.; Siegel, N.; Brooker, G. Theoretical and experimental demonstration of resolution beyond the Rayleigh limit by FINCH fluorescence microscopic imaging. Opt. Express 2011, 19, 26249–26268. [Google Scholar] [CrossRef]
- Brooker, G.; Siegel, N.; Wang, V.; Rosen, J. Optimal resolution in Fresnel incoherent correlation holographic fluorescence microscopy. Opt. Express 2011, 19, 5047–5062. [Google Scholar] [CrossRef]
- Rosen, J.; Brooker, G. Fresnel incoherent correlation holography (FINCH): A review of research. Adv. Opt. Technol. 2012, 1, 151–169. [Google Scholar] [CrossRef]
- Brooker, G.; Siegel, N.; Rosen, J.; Hashimoto, N.; Kurihara, M.; Tanabe, A. In-line FINCH super resolution digital holographic fluorescence microscopy using a high efficiency transmission liquid crystal GRIN lens. Opt. Lett. 2013, 38, 5264–5267. [Google Scholar] [CrossRef]
- Kashter, Y.; Vijayakumar, A.; Miyamoto, Y.; Rosen, J. Enhanced super resolution using Fresnel incoherent correlation holography with structured illumination. Opt. Lett. 2016, 41, 1558–1561. [Google Scholar] [CrossRef]
- Tahara, T.; Kanno, T.; Arai, Y.; Ozawa, T. Single-shot phase-shifting incoherent digital holography. J. Opt. 2017, 19, 065705. [Google Scholar] [CrossRef]
- Nobukawa, T.; Muroi, T.; Katano, Y.; Kinoshita, N.; Ishii, N. Single-shot phase-shifting incoherent digital holography with multiplexed checkerboard phase gratings. Opt. Lett. 2018, 43, 1698–1701. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Katkus, T.; Lundgaard, S.; Linklater, D.; Ivanova, E.P.; Ng, S.H.; Juodkazis, S. Fresnel incoherent correlation holography with single camera shot. Opto-Electron. Adv. 2020, 3, 200004. [Google Scholar] [CrossRef]
- Marar, A.; Kner, P. Three-dimensional nanoscale localization of point-like objects using self-interference digital holography. Opt. Lett. 2020, 45, 591–594. [Google Scholar] [CrossRef]
- Potcoava, M.; Mann, C.; Art, J.; Alford, S. Spatio-temporal performance in an incoherent holography lattice light-sheet microscope (IHLLS). Opt. Express 2021, 29, 23888–23901. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T.; Koujin, T.; Matsuda, A.; Ishii, A.; Ito, T.; Ichihashi, Y.; Oi, R. Incoherent color digital holography with computational coherent superposition for fluorescence imaging [Invited]. Appl. Opt. 2021, 60, A260–A267. [Google Scholar] [CrossRef] [PubMed]
- Anand, V.; Katkus, T.; Ng, S.H.; Juodkazis, S. Review of Fresnel incoherent correlation holography with linear and nonlinear correlations [Invited]. Chin. Opt. Lett. 2021, 19, 020501. [Google Scholar] [CrossRef]
- Tahara, T.; Ito, T.; Ichihashi, Y.; Oi, R. Multiwavelength three-dimensional microscopy with spatially incoherent light, based on computational coherent superposition. Opt. Lett. 2020, 45, 2482–2485. [Google Scholar] [CrossRef]
- Hara, T.; Tahara, T.; Ichihashi, Y.; Oi, R.; Ito, T. Multiwavelength-multiplexed phase-shifting incoherent color digital holography. Opt. Express 2020, 28, 10078–10089. [Google Scholar] [CrossRef]
- Rosen, J.; Alford, S.; Anand, V.; Art, J.; Bouchal, P.; Bouchal, Z.; Erdenebat, M.-U.; Huang, L.; Ishii, A.; Juodkazis, S.; et al. Roadmap on recent progress in FINCH technology. J. Imaging 2021, 7, 197. [Google Scholar] [CrossRef]
- Kelner, R.; Rosen, J. Spatially incoherent single channel digital Fourier holography. Opt. Lett. 2012, 37, 3723–3725. [Google Scholar] [CrossRef]
- Pedrini, G.; Li, H.; Faridian, A.; Osten, W. Digital holography of self-luminous objects by using a Mach–Zehnder setup. Opt. Lett. 2012, 37, 713–715. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography—A new type of incoherent digital holograms. Opt. Express 2016, 24, 12430–12441. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Rosen, J. Spectrum and space resolved 4D imaging by coded aperture correlation holography (COACH) with diffractive objective lens. Opt. Lett. 2017, 42, 947–950. [Google Scholar] [CrossRef] [PubMed]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography system with improved performance [Invited]. Appl. Opt. 2017, 56, F67–F77. [Google Scholar] [CrossRef] [PubMed]
- Vijayakumar, A.; Rosen, J. Interferenceless coded aperture correlation holography—A new technique for recording incoherent digital holograms without two-wave interference. Opt. Express 2017, 25, 13883–13896. [Google Scholar] [CrossRef] [PubMed]
- Ables, J.G. Fourier transform photography: A new method for X-ray astronomy. Proc. Astron. Soc. Aust. 1968, 1, 172–173. [Google Scholar] [CrossRef]
- Rai, M.R.; Rosen, J. Noise suppression by controlling the sparsity of the point spread function in interferenceless coded aperture correlation holography (I-COACH). Opt. Express 2019, 27, 24311–24323. [Google Scholar] [CrossRef] [PubMed]
- Fleisher, M.; Mahlab, U.; Shamir, J. Entropy optimized filter for pattern recognition. Appl. Opt. 1990, 29, 2091–2098. [Google Scholar] [CrossRef]
- Kotzer, T.; Rosen, J.; Shamir, J. Multiple-object input in nonlinear correlation. Appl. Opt. 1993, 32, 1919–1932. [Google Scholar] [CrossRef]
- Rai, M.R.; Vijayakumar, A.; Rosen, J. Nonlinear adaptive three-dimensional imaging with interferenceless coded aperture correlation holography (I-COACH). Opt. Express 2018, 26, 18143–18154. [Google Scholar] [CrossRef]
- Rai, M.R.; Rosen, J. Resolution-enhanced imaging using interferenceless coded aperture correlation holography with sparse point response. Sci. Rep. 2020, 10, 5033. [Google Scholar] [CrossRef]
- Rai, M.R.; Vijayakumar, A.; Ogura, Y.; Rosen, J. Resolution enhancement in nonlinear interferenceless COACH with point response of subdiffraction limit patterns. Opt. Express 2019, 27, 391–403. [Google Scholar] [CrossRef]
- Rai, M.R.; Vijayakumar, A.; Rosen, J. Superresolution beyond the diffraction limit using phase spatial light modulator between incoherently illuminated objects and the entrance of an imaging system. Opt. Lett. 2019, 44, 1572–1575. [Google Scholar] [CrossRef] [PubMed]
- Rai, M.R.; Vijayakumar, A.; Rosen, J. Extending the field of view by a scattering window in an I-COACH system. Opt. Lett. 2018, 43, 1043–1046. [Google Scholar] [CrossRef] [PubMed]
- Rai, M.R.; Rosen, J. Depth-of-field engineering in coded aperture imaging. Opt. Express 2021, 29, 1634–1648. [Google Scholar] [CrossRef] [PubMed]
- Hai, N.; Rosen, J. Single viewpoint tomography using point spread functions of tilted pseudo-nondiffracting beams in interferenceless coded aperture correlation holography with nonlinear reconstruction. SSRN 2023. [Google Scholar] [CrossRef]
- Dubey, N.; Kumar, R.; Rosen, J. Multi-wavelength imaging with extended depth of field using coded apertures and radial quartic phase functions. 2023; submitted for publication. [Google Scholar]
- Anand, V.; Ng, S.; Katkus, T.; Juodkazis, S. White light three-dimensional imaging using a quasi-random lens. Opt. Express 2021, 29, 15551–15563. [Google Scholar] [CrossRef]
- Mukherjee, S.; Vijayakumar, A.; Rosen, J. Spatial light modulator aided noninvasive imaging through scattering layers. Sci. Rep. 2019, 9, 17670. [Google Scholar] [CrossRef]
- Rey, J.J.; Wirth, A.; Jankevics, A.; Landers, F.; Rohweller, D.; Chen, C.B.; Bronowicki, A. A deployable, annular, 30 m telescope, space-based observatory. Proc. SPIE 2014, 9143, 18. [Google Scholar]
- Bulbul, A.; Rosen, J. Partial aperture imaging system based on sparse point spread holograms and nonlinear cross-correlations. Sci. Rep. 2020, 10, 21983. [Google Scholar] [CrossRef]
- Merkle, F. Synthetic-aperture imaging with the European Very Large Telescope. J. Opt. Soc. Am. A 1988, 5, 904–913. [Google Scholar] [CrossRef]
- Bulbul, A.; Vijayakumar, A.; Rosen, J. Superresolution far-field imaging by coded phase reflectors distributed only along the boundary of synthetic apertures. Optica 2018, 5, 1607–1616. [Google Scholar] [CrossRef]
- Desai, J.P.; Kumar, R.; Rosen, J. Optical incoherent imaging using annular synthetic aperture with superposition of phase-shifted optical transfer functions. Opt. Lett. 2022, 47, 4012–4015. [Google Scholar] [CrossRef]
- Rosen, J.; Anand, V.; Rai, M.R.; Mukherjee, S.; Bulbul, A. Review of 3D imaging by coded aperture correlation holography (COACH). Appl. Sci. 2019, 9, 605. [Google Scholar] [CrossRef]
- Rosen, J.; Hai, N.; Rai, M.R. Recent progress in digital holography with dynamic diffractive phase apertures [Invited]. Appl. Opt. 2022, 61, B171–B180. [Google Scholar] [CrossRef]
- Rosen, J.; Bulbul, A.; Hai, N.; Rai, M.R. Coded Aperture Correlation Holography (COACH)—A Research Journey from 3D Incoherent Optical Imaging to Quantitative Phase Imaging. In Holography–Recent Advances and Applications, 1st ed.; Rosen, J., Ed.; IntechOpen: London, UK, 2023. [Google Scholar]
- Hai, N.; Rosen, J. Interferenceless and motionless method for recording digital holograms of coherently illuminated 3D objects by coded aperture correlation holography system. Opt. Express 2019, 27, 24324–24339. [Google Scholar] [CrossRef]
- Hai, N.; Rosen, J. Phase contrast-based phase retrieval: A bridge between qualitative phase contrast and quantitative phase imaging by phase retrieval algorithms. Opt. Lett. 2020, 45, 5812–5815. [Google Scholar] [CrossRef]
- Hai, N.; Kumar, R.; Rosen, J. Single-shot TIE using polarization multiplexing (STIEP) for quantitative phase imaging. Opt. Lasers Eng. 2022, 151, 106912. [Google Scholar] [CrossRef]
- Hai, N.; Rosen, J. Single-plane and multiplane quantitative phase imaging by self-reference on-axis holography with a phase-shifting method. Opt. Express 2021, 29, 24210–24225. [Google Scholar] [CrossRef]
- Hai, N.; Rosen, J. Coded aperture correlation holographic microscope for single-shot quantitative phase and amplitude imaging with extended field of view. Opt. Express 2020, 28, 27372–27386. [Google Scholar] [CrossRef]
- Dubey, N.; Kumar, R.; Rosen, J. COACH-based Shack-Hartmann wavefront sensor with an array of phase coded masks. Opt. Express 2021, 29, 31859–31874. [Google Scholar] [CrossRef]
- Bulbul, A.; Hai, N.; Rosen, J. Coded aperture correlation holography (COACH) with a superior lateral resolution of FINCH and axial resolution of conventional direct imaging systems. Opt. Express 2021, 29, 42106–42118. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosen, J. Advanced Imaging Methods Using Coded Aperture Digital Holography. Eng. Proc. 2023, 34, 2. https://doi.org/10.3390/HMAM2-14122
Rosen J. Advanced Imaging Methods Using Coded Aperture Digital Holography. Engineering Proceedings. 2023; 34(1):2. https://doi.org/10.3390/HMAM2-14122
Chicago/Turabian StyleRosen, Joseph. 2023. "Advanced Imaging Methods Using Coded Aperture Digital Holography" Engineering Proceedings 34, no. 1: 2. https://doi.org/10.3390/HMAM2-14122
APA StyleRosen, J. (2023). Advanced Imaging Methods Using Coded Aperture Digital Holography. Engineering Proceedings, 34(1), 2. https://doi.org/10.3390/HMAM2-14122





